HTML5-Canvas-Zeichen-Tutorial (6) – arcTo-Methode zum Zeichnen von Kurven in Canvas_HTML5-Tutorial-Fähigkeiten

Im vorherigen Artikel ging es um die arc-Methode von canvas, und in diesem Artikel geht es um die damit verbundene arcTo-Methode.
arc und arcTo sind vom Namen her ähnlich. arcTo ist auch eine Methode zum Zeichnen von Kurven, und die von ihm gezeichnete Kurve ist ebenfalls ein Bogen eines perfekten Kreises. Aber seine Parameter sind einfach nicht kompatibel mit arc~
ctx.arcTo(x1,y1,x2,y2,radius); Die Parameter von arcTo umfassen zwei Punkte, und diese beiden Punkte stellen nicht den Mittelpunkt des Kreises dar. Nur der letzte Parameter ist der Radius des Kreises, was darauf hinweist, dass arcTo eine gewisse Beziehung zum Kreis hat.
Es gibt nur sehr wenige Artikel über arcTo im Internet, und ich habe endlich einen aus einem anderen Land gefunden, und es gibt keine intuitiven Tools zum Zeichnen auf Leinwand, sodass ich mich lange Zeit nur auf Vermutungen verlassen konnte . .
Zur intuitiven Beschreibung habe ich eine Hilfsmethode übernommen: Überall dort, wo arcTo gezeichnet wird, verwende ich auch lineTo, um die entsprechenden Punkte zu zeichnen, um ihre Beziehung zu sehen. Zeichnen Sie einfach Hilfslinien.

Code kopieren

Der Code lautet wie folgt:

var x0=100,
y0 =400,
x1 = 500,
y1 = 400,
x2 = 450,
ctx.beginPath(); x0,y0 );
ctx.StrokeStyle = "#f00"; ();
ctx.beginPath();
ctx.StrokeStyle = "rgba(0,0,0,0.5)"
ctx.moveTo(x0, y0);
ctx.lineTo(x1,y1);
ctx.fillText('x1,y1',x1 10,y1 10)
ctx.lineTo(x2,y2); .fillText( 'x2,y2',x2 10,y2)
ctx.Stroke();


Es scheint eine Menge Code zu sein, aber es ist eigentlich sehr einfach. Ich habe ein paar Variablen verwendet, um die Koordinatenwerte zu speichern, und der Rest waren Canvas-Operationen.
Variablenbeschreibung: x0, y0 sind die Koordinaten des Startpunkts, x1, y1 sind die Koordinaten des ersten Punkts, x2, y2 sind die Koordinaten des zweiten Punkts. Die von lineTo gezeichnete gerade Linie ist eine durchscheinende schwarze 1-Pixel-Linie, und die von arcTo gezeichnete Linie ist eine rote 2-Pixel-Linie.
Aktualisieren Sie die Seite und Sie sehen das Bild unten.

Ich muss sagen, dass diese rote Linie wie ein Haken aussieht.
Dann wird die Regel von arcTo gefunden. Sie verläuft tatsächlich durch den Startpunkt, den ersten Punkt, und die beiden geraden Linien am zweiten Punkt und bildet einen eingeschlossenen Winkel, und diese beiden Linien sind auch Tangenten an den Parameterkreis.
Der Radius des Kreises bestimmt, wo der Kreis die Linie tangiert. Genau wie ein Ball, der in einen toten Winkel rollt, gilt: Je kleiner der Ball, desto weiter rollt er hinein und näher an den toten Punkt; das Gegenteil gilt für einen größeren Ball.
Dies ist ein sehr ernstes akademisches Problem, bitte seien Sie nicht JJ.

Lasst uns den Ball größer machen!

Code kopieren


Der Code lautet wie folgt:

ctx.arcTo(x1, y1,x2 ,y2,50); //Ändere den Radius auf 50

Wie im Bild zu sehen ist, ist der Bogen sehr groß geworden und nicht einmal tangential zur Geraden.
Natürlich sind sie tatsächlich immer noch tangential, denn die Tangente erstreckt sich ins Unendliche.

Wir erforschen weiter, vergrößern den Kreis weiter und verkürzen den Abstand zwischen dem Startpunkt und dem ersten Punkt.

Code kopieren


Der Code lautet wie folgt:

var x0=400; /Startpunkt x Die Koordinaten ändern sich von 100 auf 400 ... ctx.arcTo(x1,y1,x2,y2,100); //Der Radius des Kreises erhöht sich auf 100 und dann werden Sie sehen so eine seltsame Form.

Ursprünglich war es ein Haken, aber jetzt wurde er abrupt gebogen, und zwar sogar in die entgegengesetzte Richtung! Es ist ein bisschen wie ein Weinflaschenregal.
Bitte beachten Sie jedoch, dass dieser Kreis immer noch eine Tangente an die beiden Linien ist! Es ist nur so, dass die Länge der beiden Linien jetzt nicht mehr dem Kreis entsprechen kann! Er hat beide Leitungen drahtlos verlängert!
Wann wird dieser Hakengriff umgekehrt? Wenn Sie gut in Geometrie sind, können Sie versuchen, die Tangentengleichung zwischen einem Punkt und einem Kreis zu verstehen.

Es gibt einen sehr wichtigen Punkt in der arcTo-Methode. Dieser wichtige Punkt ist (x1, y1) im Code, solange sein Abstand zum Tangentenpunkt des Kreises seinen Abstand zum Startpunkt (x0, y0) überschreitet ), Es kommt zu einer Umkehr.
Aus dem Bild können wir ersehen, dass sich die Koordinaten des Punktes (x2, y2) unendlich ändern können. Solange es sich immer um einen Punkt auf der Tangente handelt, bleibt der gezeichnete Graph unverändert von arcTo Nichts wird sich ändern. Dies erfordert besondere Aufmerksamkeit.

Lassen Sie mich mein Wissen über Geometrie nutzen, das in der Tabelle nicht verfügbar ist, um diesen Vorschlag zu überprüfen. Um die Berechnung zu erleichtern, ändere ich zunächst den Winkel zwischen den beiden Linien auf 90 Grad.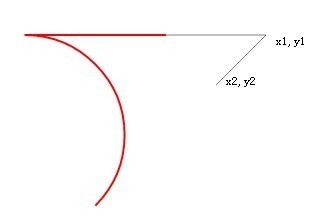

Code kopieren


Der Code lautet wie folgt:

var x0=100,
y0=400,
x1 = 500,
y1 = 400,
x2 = 500,
y2 = 450; 🎜>
Nach dem Wechsel öffnet es bei 90 Grad! Wir halten den Radius des Balls konstant. Nach der Aktualisierung:

Wir vergrößern y2, d. h. verlängern eine Tangente und verwandeln sie in 550. Nach dem Auffrischen: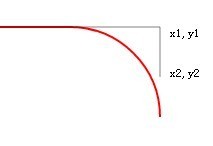

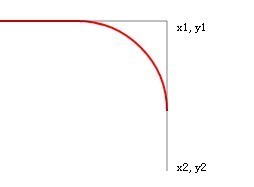Die Tangente wird verlängert, aber die von arcTo gezeichnete rote Linie hat keine Änderung.