Heim >Technologie-Peripheriegeräte >KI >Google: LLM kann keine Inferenzfehler finden, kann diese aber korrigieren
Google: LLM kann keine Inferenzfehler finden, kann diese aber korrigieren
- 王林nach vorne
- 2023-11-27 14:39:201218Durchsuche
In diesem Jahr sind große Sprachmodelle (LLM) in den Mittelpunkt großer Aufmerksamkeit im Bereich der künstlichen Intelligenz gerückt. LLM hat bei verschiedenen Aufgaben der Verarbeitung natürlicher Sprache (NLP), insbesondere beim logischen Denken, erhebliche Fortschritte gemacht. Bei komplexen Argumentationsaufgaben muss die Leistung von LLM jedoch noch verbessert werden.
Kann LLM feststellen, dass es Fehler in seiner eigenen Argumentation gibt? Kürzlich ergab eine gemeinsam von der Universität Cambridge und Google Research durchgeführte Studie, dass LLM Denkfehler nicht selbst erkennen kann, aber die in der Studie vorgeschlagene Backtracking-Methode verwenden kann, um die Fehler zu korrigieren Papieradresse: https://arxiv.org/pdf/2311.08516.pdf
 Datensatzadresse: https://github.com/WHGTyen/BIG-Bench-Mistake
Datensatzadresse: https://github.com/WHGTyen/BIG-Bench-Mistake
- Dieses Papier hat verursacht Einige Kontroversen, jemand hat Einwände dagegen erhoben. Beispielsweise bemerkte jemand bei Hacker News, dass der Titel des Papiers übertrieben und ein bisschen Clickbait sei. Andere kritisierten, dass die in dem Artikel vorgeschlagene Methode zur Korrektur logischer Fehler auf Mustervergleichen und nicht auf logischen Methoden basiert. Diese Methode ist anfällig für Fehler.
- Huang et al noch“ Weisen Sie darauf hin: Selbstkorrektur kann den Stil und die Qualität der Modellausgabe wirksam verbessern, es gibt jedoch kaum Hinweise darauf, dass LLM in der Lage ist, seine eigenen Argumentations- und Logikfehler ohne externes Feedback zu identifizieren und zu korrigieren. Beispielsweise nutzen sowohl Reflexion als auch RCI das Korrekturergebnis der Grundwahrheit als Signal, um den Selbstkorrekturzyklus zu stoppen. Das Forschungsteam der University of Cambridge und Google Research schlugen eine neue Idee vor: den Selbstkorrekturprozess in zwei Phasen zu unterteilen: Fehlererkennung und Ausgabekorrektur
Fehlererkennung ist eine grundlegende Fähigkeit zum Denken verwendet in Es wurde umfassend in den Bereichen Philosophie, Psychologie und Mathematik untersucht und angewendet und hat zu Konzepten wie kritischem Denken sowie logischen und mathematischen Irrtümern geführt. Man kann davon ausgehen, dass die Fähigkeit zur Fehlererkennung auch eine wichtige Voraussetzung für LLM sein sollte. Unsere Ergebnisse zeigen jedoch, dass moderne LLMs derzeit nicht in der Lage sind, Fehler zuverlässig zu erkennen.
Bei der Ausgabekorrektur handelt es sich um eine teilweise oder vollständige Änderung der zuvor generierten Ausgabe. Selbstkorrektur bedeutet, dass die Korrektur von demselben Modell durchgeführt wird, das die Ausgabe generiert hat. Obwohl LLM nicht in der Lage ist, Fehler zu erkennen, zeigt dieses Papier, dass LLM die Ausgabe mithilfe einer Backtracking-Methode korrigieren kann, wenn Informationen über den Fehler bereitgestellt werden (z. B. durch ein kleines überwachtes Belohnungsmodell).
- Die Hauptbeiträge dieses Artikels umfassen:
- Mit der Denkketten-Prompt-Design-Methode kann jede Aufgabe in eine Fehlererkennungsaufgabe umgewandelt werden. Zu diesem Zweck sammelten und veröffentlichten die Forscher einen von PaLM generierten CoT-Trajektorieninformationsdatensatz BIG-Bench Mistake, der den Ort des ersten logischen Fehlers markierte. Forscher sagen, dass BIG-Bench Mistake der erste Datensatz seiner Art ist, der nicht auf mathematische Probleme beschränkt ist.
In diesem Artikel wird vorgeschlagen, die Backtracking-Methode zu verwenden, um die Ausgabe zu korrigieren und falsche Positionsinformationen zu verwenden, um die Leistung bei der ursprünglichen Aufgabe zu verbessern. Untersuchungen haben gezeigt, dass diese Methode eine ansonsten falsche Ausgabe mit minimalen Auswirkungen auf eine ansonsten korrekte Ausgabe korrigieren kann.
- In diesem Artikel wird die Backtracking-Methode als eine Form des „verbalen Verstärkungslernens“ erläutert, mit der eine iterative Verbesserung der CoT-Ausgabe ohne Gewichtsaktualisierungen erreicht werden kann. Die Forscher schlugen vor, dass Backtracking durch die Verwendung eines trainierten Klassifikators als Belohnungsmodell verwendet werden kann, und sie demonstrierten auch experimentell die Wirksamkeit von Backtracking bei unterschiedlicher Genauigkeit von Belohnungsmodellen.
- BIG-Bench-Fehlerdatensatz
- BIG-Bench enthält 2186 Flugbahninformationssätze im CoT-Stil. Jede Trajektorie wurde von PaLM 2-L-Unicorn generiert und der Ort des ersten logischen Fehlers wurde mit Anmerkungen versehen. Tabelle 1 zeigt ein Beispiel einer Trajektorie, bei der der Fehler in Schritt 4 auftritt die Dyck-Sprache.
Um die Fragen jeder Aufgabe zu beantworten, verwendeten sie die CoT-Prompt-Design-Methode, um PaLM 2 aufzurufen. Um die CoT-Trajektorien in klare Schritte zu unterteilen, haben sie die in „React: Synergizing Reasoning and Acting in Language Models“ vorgeschlagene Methode übernommen, um jeden Schritt separat zu generieren und Zeilenumbrüche als Stoppmarkierungen zu verwenden
Beim Generieren aller Trajektorien Datensatz, wenn Temperatur = 0, wird die Richtigkeit der Antwort durch eine genaue Übereinstimmung bestimmt. 3.5-Turbo ist in Tabelle 4 dargestellt
Jede Frage hat zwei mögliche Antworten: entweder richtig oder falsch. Wenn es sich um einen Fehler handelt, gibt der Wert N den Schritt an, bei dem der erste Fehler aufgetreten ist
 Alle Modelle wurden mit den gleichen 3 Eingabeaufforderungen eingegeben. Sie verwendeten drei verschiedene Prompt-Design-Methoden:
Alle Modelle wurden mit den gleichen 3 Eingabeaufforderungen eingegeben. Sie verwendeten drei verschiedene Prompt-Design-Methoden: Direktes Prompt-Design auf Track-Ebene
Direktes Prompt-Design auf Schrittebene
- CoT-Prompt-Design auf Schrittebene
- Der Inhalt, der benötigt wird neu geschrieben werden soll: Verwandte Diskussion
Das zeigt, dass LLMs auf dem aktuellen Stand der Technik selbst in den einfachsten und klarsten Fällen Schwierigkeiten haben, Fehler zu finden. Im Gegensatz dazu können Menschen Fehler ohne spezifisches Fachwissen und mit hoher Konsistenz finden.
Forscher spekulieren, dass die Unfähigkeit von LLM, Fehler zu erkennen, der Hauptgrund dafür ist, dass LLM Denkfehler nicht selbst korrigieren kann.
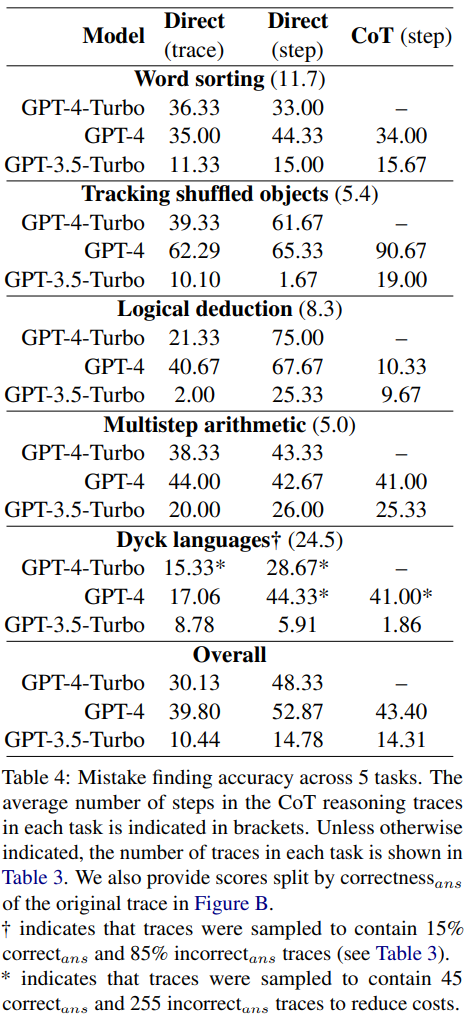
prompter Vergleich der Entwurfsmethoden
Die Forscher fanden heraus, dass vom direkten Ansatz auf Trajektorienebene über den Ansatz auf Stufenebene bis zum CoT-Ansatz die Genauigkeit der Trajektorie ohne Fehler erheblich abnahm. Abbildung 1 zeigt diesen Kompromiss
Die Forscher glauben, dass der Grund dafür möglicherweise in der Anzahl der Modellausgaben liegt. Alle drei Methoden erfordern die Generierung immer komplexerer Ausgaben: Prompt-Design-Methoden, die direkt Trajektorien generieren, erfordern einen einzelnen Token, Prompt-Design-Methoden, die direkt Schritte generieren, erfordern ein Token pro Schritt und CoT-Prompt-Design-Methoden auf Schrittebene erfordern für jeden Schritt mehrere Sätze. Wenn eine gewisse Wahrscheinlichkeit einer Fehlerrate pro Build-Aufruf besteht, ist die Wahrscheinlichkeit, dass das Modell mindestens einen Fehler erkennt, umso größer, je mehr Aufrufe pro Trace vorhanden sind
 Wenige Beispiele mit Fehlerort als Proxy für die Richtigkeit des Prompt-Designs
Wenige Beispiele mit Fehlerort als Proxy für die Richtigkeit des Prompt-DesignsDie Forscher untersuchten, ob diese Prompt-Design-Methoden zuverlässig die Richtigkeit einer Flugbahn und nicht deren falsche Position bestimmen können.
Sie berechneten den durchschnittlichen F1-Score basierend darauf, ob das Modell korrekt vorhersagen kann, ob Fehler in der Flugbahn vorliegen. Liegt ein Fehler vor, gilt die vom Modell vorhergesagte Flugbahn als „falsche Antwort“. Andernfalls wird die vom Modell vorhergesagte Flugbahn als „richtige Antwort“ betrachtet.
Unter Verwendung von „richtige_ans“ und „falsche_ans“ als positive Bezeichnungen und gewichtet nach der Häufigkeit des Vorkommens jeder Bezeichnung berechneten die Forscher den durchschnittlichen F1-Score und die Ergebnisse sind siehe Tabelle 5.
Dieser gewichtete F1-Score zeigt, dass die Suche nach Fehlern anhand der Eingabeaufforderung eine schlechte Strategie zur Bestimmung der Richtigkeit der endgültigen Antwort ist.
Backtracking

Huang et al. wiesen darauf hin, dass LLM Logikfehler ohne externes Feedback nicht selbst korrigieren kann. In vielen realen Anwendungen ist jedoch häufig kein externes Feedback verfügbar. In dieser Studie haben die Forscher eine Alternative gewählt: einen einfachen Klassifikator, der auf einer kleinen Menge externer Rückmeldungen trainiert wird. Ähnlich wie Belohnungsmodelle beim traditionellen Reinforcement Learning kann dieser Klassifikator alle logischen Fehler in CoT-Trajektorien erkennen, bevor er sie an das Generatormodell zurückgibt, um die Ausgabe zu verbessern. Wenn Sie die Verbesserung maximieren möchten, können Sie mehrere Iterationen durchführen.
Forscher schlugen eine einfache Methode vor, um die Ausgabe des Modells zu verbessern, indem die Position logischer Fehler zurückverfolgt wird
- Das Modell generiert zunächst eine anfängliche CoT-Trajektorie. In Experimenten stellen Sie die Temperatur = 0 ein.
- Verwenden Sie dann das Belohnungsmodell, um den Ort des Fehlers in der Trajektorie zu bestimmen.
- Wenn keine Fehler vorliegen, fahren Sie mit dem nächsten Titel fort. Wenn Fehler auftreten, veranlassen Sie das Modell erneut, die gleichen Schritte auszuführen, dieses Mal jedoch mit Temperatur = 1, wodurch 8 Ausgaben erzeugt werden. Hier wird die gleiche Eingabeaufforderung zusammen mit einer Teilverfolgung aller Schritte vor dem fehlerhaften Schritt verwendet.
- Filtern Sie in diesen 8 Ausgaben Optionen heraus, die mit dem vorherigen Fehler identisch sind. Wählen Sie dann aus den verbleibenden Ausgaben diejenige mit der höchsten logarithmischen Wahrscheinlichkeit aus.
- Ersetzen Sie abschließend den vorherigen Schritt durch den neuen regenerierten Schritt, setzen Sie die Temperatur auf 0 zurück und fahren Sie mit der Generierung der verbleibenden Schritte der Flugbahn fort.
Im Vergleich zur vorherigen Selbstkorrekturmethode hat diese Backtracking-Methode viele Vorteile:
- Die neue Backtracking-Methode erfordert keine Vorkenntnisse der Antwort. Stattdessen stützt es sich auf Informationen über logische Fehler (z. B. aus einem trainierten Belohnungsmodell), die mithilfe des Belohnungsmodells Schritt für Schritt ermittelt werden können. Logische Fehler können in der korrekten_ans-Trajektorie auftreten oder auch nicht.
- Die Traceback-Methode basiert nicht auf einem bestimmten Eingabeaufforderungstext oder einer bestimmten Formulierung, wodurch entsprechende Präferenzen reduziert werden.
- Im Vergleich zu Methoden, die die Regenerierung der gesamten Trajektorie erfordern, kann die Backtracking-Methode die Rechenkosten reduzieren, indem bekannte logisch korrekte Schritte wiederverwendet werden.
- Backtracking-Methoden können die Qualität von Zwischenschritten direkt verbessern, was in Szenarien nützlich sein kann, in denen korrekte Schritte erforderlich sind (z. B. beim Generieren von Lösungen für mathematische Probleme), und gleichzeitig die Interpretierbarkeit verbessern.
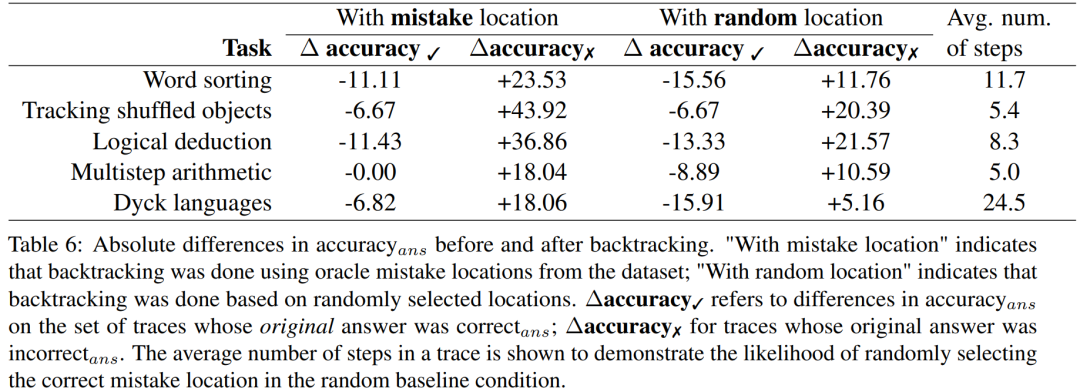
Die Forscher verwendeten den BIG-Bench Mistake-Datensatz, um Experimente durchzuführen, um zu untersuchen, ob die Backtracking-Methode LLM dabei helfen kann, Logikfehler zu korrigieren. Die experimentellen Ergebnisse finden Sie in Tabelle 6.
Für die Ergebnisse falscher Antwortverläufe muss die Genauigkeit neu berechnet werden

Diese Bewertungsergebnisse zeigen, dass der Gewinn durch die Korrektur falscher Antwortverläufe größer ist als der Verlust, der durch die Änderung der ursprünglichen richtigen Antwort verursacht wird. Darüber hinaus erzielen zufällige Benchmarks zwar ebenfalls Verbesserungen, diese sind jedoch deutlich geringer als bei Verwendung echter Fehlerorte. Beachten Sie, dass es bei randomisierten Benchmarks eher zu Leistungssteigerungen bei Aufgaben mit weniger Schritten kommt, da die Wahrscheinlichkeit größer ist, dass der Ort des wahren Fehlers gefunden wird.
Um herauszufinden, welches Belohnungsmodell für Genauigkeitsstufen erforderlich ist, wenn keine guten Labels verfügbar sind, experimentierten sie mit der Verwendung von Backtracking durch ein simuliertes Belohnungsmodell. Das Designziel dieses simulierten Belohnungsmodells besteht darin, Labels mit unterschiedlichen Genauigkeitsstufen zu erzeugen. Sie verwenden precision_RM, um die Genauigkeit des Simulationsbelohnungsmodells an einer bestimmten Fehlerstelle darzustellen.
Wenn die Genauigkeit_RM eines bestimmten Belohnungsmodells X % beträgt, wird in X % der Fälle der Fehlerort aus dem BIG-Bench-Fehler verwendet. Für die verbleibenden (100 − X) % wird eine Fehlerstelle zufällig ausgewählt. Um das Verhalten eines typischen Klassifikators zu simulieren, werden Fehlerorte so abgetastet, dass sie der Verteilung des Datensatzes entsprechen. Die Forscher fanden auch Wege, um sicherzustellen, dass der falsche Ort der Probe nicht mit dem richtigen Ort übereinstimmte. Die Ergebnisse sind in Abbildung 2 dargestellt.
Es ist zu beobachten, dass sich die Δ-Genauigkeit zu stabilisieren beginnt, wenn die Verlustrate 65 % erreicht. Tatsächlich übersteigt bei den meisten Aufgaben die ΔGenauigkeit ✓ bereits die ΔGenauigkeit ✗, wenn die Genauigkeit_RM etwa 60–70 % beträgt. Dies zeigt, dass eine höhere Genauigkeit zwar zu besseren Ergebnissen führt, das Backtracking jedoch auch ohne Goldstandard-Fehlerortungsetiketten funktioniert
Das obige ist der detaillierte Inhalt vonGoogle: LLM kann keine Inferenzfehler finden, kann diese aber korrigieren. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- php „7-Tage-Devil-Trainingslager' – kostenlose Live-Kursanmeldung! ! ! ! ! !
- Was ist das CSS-Box-Modell?
- Was ist das OSI-Modell?
- Programmierer sind in Gefahr! Es heißt, dass OpenAI weltweit Outsourcing-Truppen rekrutiert und ChatGPT-Code-Farmer Schritt für Schritt schult
- Yunshenchen und Shengteng CANN arbeiten zusammen, um ein ROS-Trainingslager für die Entwicklung vierbeiniger Roboterhunde zu eröffnen


 Alle Modelle wurden mit den gleichen 3 Eingabeaufforderungen eingegeben. Sie verwendeten drei verschiedene Prompt-Design-Methoden:
Alle Modelle wurden mit den gleichen 3 Eingabeaufforderungen eingegeben. Sie verwendeten drei verschiedene Prompt-Design-Methoden: 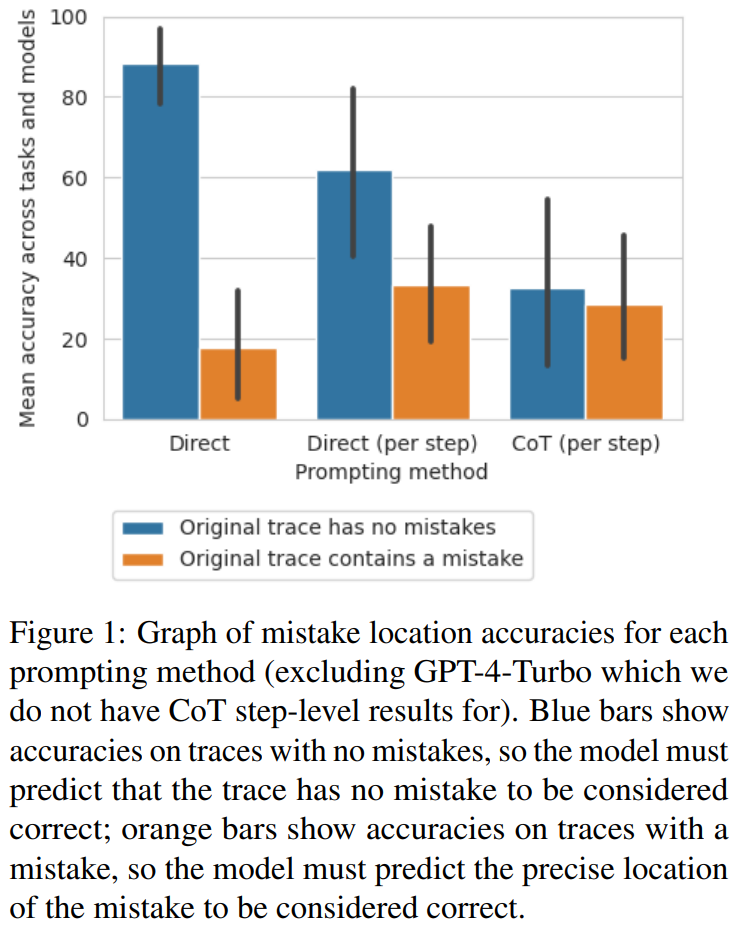 Wenige Beispiele mit Fehlerort als Proxy für die Richtigkeit des Prompt-Designs
Wenige Beispiele mit Fehlerort als Proxy für die Richtigkeit des Prompt-Designs