Haben Sie schon einmal einen Mobius-Streifen selbst gemacht?
Der Möbius-Streifen ist eine eigenartige mathematische Struktur. Es ist eigentlich sehr einfach, solch eine schöne einseitige Oberfläche zu konstruieren, sogar ein Kind kann es problemlos fertigstellen. Sie müssen lediglich ein Stück Papierband nehmen, es einmal drehen und die beiden Enden zusammenkleben. Ein solch einfach herzustellender Möbius-Streifen weist jedoch komplexe Eigenschaften auf, die seit langem das Interesse der Mathematiker wecken. Vor kurzem beschäftigte Forscher eine scheinbar einfache Frage: Wie lang muss das Papierband mindestens sein, um einen Möbius-Streifen herzustellen? Richard Evan Schwartz von der Brown University sagte, dass dieses Problem für Möbius-Streifen nicht gelöst sei, weil sie „eingebettet“ und nicht „eingetaucht“ seien, was bedeutet, dass sie sich nicht gegenseitig durchdringen oder kreuzen. Ein Möbius-Streifen ist eigentlich ein Hologramm, eine in den dreidimensionalen Raum projizierte Figur: Bei einem „eingebetteten“ Möbius-Streifen können sich mehrere Schichten von Streifen überlappen, ein bisschen wie ein Geist, der durch eine Wand geht; Streifen gibt es keine solche Überlappung.  1977 stellten die Mathematiker Charles Sidney Weaver und Benjamin Rigler Halpern dieses Problem minimaler Abmessungen und stellten fest, dass es einfach wäre, wenn die Möbius-Streifen sich selbst schneiden dürften. Das verbleibende Problem besteht dann darin, zu bestimmen, wie viel Platz benötigt wird, um Selbstüberschneidungen zu vermeiden. Halpern und Weaver schlugen eine Mindestgröße vor, konnten diese Idee jedoch nicht beweisen, weshalb sie als Halpern-Weaver-Vermutung bekannt wurde. Schwartz erfuhr vor vier Jahren zum ersten Mal von diesem Problem und war davon fasziniert. Jetzt hat sein Interesse neue Früchte getragen. Papieradresse: https://arxiv.org/pdf/2308.12641.pdfEr bewies Halpern in einem Preprint-Papier, das am 24. August 2023 auf arXiv.org veröffentlicht wurde – Weaver-Vermutung. Er zeigte, dass „eingebettete“ Möbius-Streifen aus Papier nur mit Seitenverhältnissen größer als
1977 stellten die Mathematiker Charles Sidney Weaver und Benjamin Rigler Halpern dieses Problem minimaler Abmessungen und stellten fest, dass es einfach wäre, wenn die Möbius-Streifen sich selbst schneiden dürften. Das verbleibende Problem besteht dann darin, zu bestimmen, wie viel Platz benötigt wird, um Selbstüberschneidungen zu vermeiden. Halpern und Weaver schlugen eine Mindestgröße vor, konnten diese Idee jedoch nicht beweisen, weshalb sie als Halpern-Weaver-Vermutung bekannt wurde. Schwartz erfuhr vor vier Jahren zum ersten Mal von diesem Problem und war davon fasziniert. Jetzt hat sein Interesse neue Früchte getragen. Papieradresse: https://arxiv.org/pdf/2308.12641.pdfEr bewies Halpern in einem Preprint-Papier, das am 24. August 2023 auf arXiv.org veröffentlicht wurde – Weaver-Vermutung. Er zeigte, dass „eingebettete“ Möbius-Streifen aus Papier nur mit Seitenverhältnissen größer als  konstruiert werden können. Wenn das Armband beispielsweise 1 cm lang ist, muss seine Breite größer als
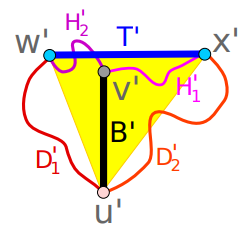
konstruiert werden können. Wenn das Armband beispielsweise 1 cm lang ist, muss seine Breite größer als  cm sein. Das Lösen dieses Rätsels erfordert mathematische Kreativität. Wenn man Standardansätze zur Lösung dieser Art von Problemen verwendet, ist es schwierig, anhand von Formeln zwischen sich selbst schneidenden und sich nicht selbst schneidenden Oberflächen zu unterscheiden. Es bedarf der geometrischen Vision von Schwartz, um diese Schwierigkeit zu überwinden, aber das kommt selten vor. In Schwartz‘ Beweis gelang es ihm, das Problem in handhabbare Teile zu zerlegen, für deren Lösung jeweils grundsätzlich nur Grundkenntnisse der Geometrie erforderlich sind. Tatsächlich probierte Schwartz mehrere Jahre lang immer wieder andere Strategien aus, bevor er eine fand, die funktionierte. Er beschloss kürzlich, das Problem erneut zu untersuchen, da er immer der Meinung war, dass die Methode, die er in einer Arbeit aus dem Jahr 2021 verwendet hatte, gültig sein sollte. Offensichtlich war seine Intuition richtig. Als er das Problem noch einmal untersuchte, bemerkte er einen Fehler im Lemma zu T-Diagrammen im vorherigen Artikel. Durch die Korrektur dieses Fehlers konnte Schwartz die Halpern-Weaver-Vermutung schnell und einfach beweisen. Schwartz selbst sagt, dass er das Problem ohne diesen Fehler schon vor drei Jahren gelöst hätte.
cm sein. Das Lösen dieses Rätsels erfordert mathematische Kreativität. Wenn man Standardansätze zur Lösung dieser Art von Problemen verwendet, ist es schwierig, anhand von Formeln zwischen sich selbst schneidenden und sich nicht selbst schneidenden Oberflächen zu unterscheiden. Es bedarf der geometrischen Vision von Schwartz, um diese Schwierigkeit zu überwinden, aber das kommt selten vor. In Schwartz‘ Beweis gelang es ihm, das Problem in handhabbare Teile zu zerlegen, für deren Lösung jeweils grundsätzlich nur Grundkenntnisse der Geometrie erforderlich sind. Tatsächlich probierte Schwartz mehrere Jahre lang immer wieder andere Strategien aus, bevor er eine fand, die funktionierte. Er beschloss kürzlich, das Problem erneut zu untersuchen, da er immer der Meinung war, dass die Methode, die er in einer Arbeit aus dem Jahr 2021 verwendet hatte, gültig sein sollte. Offensichtlich war seine Intuition richtig. Als er das Problem noch einmal untersuchte, bemerkte er einen Fehler im Lemma zu T-Diagrammen im vorherigen Artikel. Durch die Korrektur dieses Fehlers konnte Schwartz die Halpern-Weaver-Vermutung schnell und einfach beweisen. Schwartz selbst sagt, dass er das Problem ohne diesen Fehler schon vor drei Jahren gelöst hätte.  Dieses Lemma basiert auf einer Grundidee: Einige Geraden auf einem Möbiusband werden Regelflächen genannt. Schwartz wies darauf hin, dass ein Papierstreifen im Raum, auch wenn er sich in einer komplizierten Position befindet, an jedem Punkt immer noch von einer geraden Linie durchzogen ist. Man kann sich vorstellen, diese geraden Linien so zu zeichnen, dass sie den Möbiusstreifen kreuzen und beide Enden sich berühren die Grenze.In früheren Arbeiten identifizierte Schwartz zwei gerade Linien parallel zueinander und in derselben Ebene, die in jedem Möbius-Streifen ein T-förmiges Muster bildeten. Er weist darauf hin, dass es nicht offensichtlich ist, dass diese Dinge existieren und dass sie bewiesen werden müssen, was der erste Teil des Beweises des Lemmas ist. Der nächste Schritt besteht darin, das Optimierungsproblem aufzustellen und zu lösen, das das Schneiden eines Möbius-Streifens in einem Winkel entlang eines Liniensegments erfordert, das sich über die Breite des Streifens erstreckt und die endgültige Form erhält. Schwartz kam in seiner Arbeit von 2021 fälschlicherweise zu dem Schluss, dass es sich bei der Form um ein Parallelogramm handele. Diesen Sommer beschloss Schwartz, eine andere Strategie auszuprobieren. Er begann zu versuchen, das Möbiusband zu glätten. Wenn gezeigt werden könnte, dass sie in eine flache Oberfläche gepresst werden könnten, würde dieses komplexe Problem auf ein besser beherrschbares Problem der flachen Oberfläche reduziert werden. In einem Experiment schnitt Schwartz ein Möbius-Band auf und stellte fest, dass es sich nicht um ein Parallelogramm, sondern um ein Trapez handelte. Endlich ist die 50 Jahre alte Frage beantwortet. Es erfordert Mut, ein seit langem bestehendes Problem zu lösen, und das ist Schwartz‘ Stärke in der Mathematik: Er arbeitet gerne an Problemen, die relativ einfach erscheinen, in Wirklichkeit aber schwierig sind. Er wird Probleme sehen, die früheren Forschern nicht aufgefallen sind. Referenzlink: https://www.scientificamerican.com/article/mathematicians-solve-50-year-old-moebius-strip-puzzle1/
Dieses Lemma basiert auf einer Grundidee: Einige Geraden auf einem Möbiusband werden Regelflächen genannt. Schwartz wies darauf hin, dass ein Papierstreifen im Raum, auch wenn er sich in einer komplizierten Position befindet, an jedem Punkt immer noch von einer geraden Linie durchzogen ist. Man kann sich vorstellen, diese geraden Linien so zu zeichnen, dass sie den Möbiusstreifen kreuzen und beide Enden sich berühren die Grenze.In früheren Arbeiten identifizierte Schwartz zwei gerade Linien parallel zueinander und in derselben Ebene, die in jedem Möbius-Streifen ein T-förmiges Muster bildeten. Er weist darauf hin, dass es nicht offensichtlich ist, dass diese Dinge existieren und dass sie bewiesen werden müssen, was der erste Teil des Beweises des Lemmas ist. Der nächste Schritt besteht darin, das Optimierungsproblem aufzustellen und zu lösen, das das Schneiden eines Möbius-Streifens in einem Winkel entlang eines Liniensegments erfordert, das sich über die Breite des Streifens erstreckt und die endgültige Form erhält. Schwartz kam in seiner Arbeit von 2021 fälschlicherweise zu dem Schluss, dass es sich bei der Form um ein Parallelogramm handele. Diesen Sommer beschloss Schwartz, eine andere Strategie auszuprobieren. Er begann zu versuchen, das Möbiusband zu glätten. Wenn gezeigt werden könnte, dass sie in eine flache Oberfläche gepresst werden könnten, würde dieses komplexe Problem auf ein besser beherrschbares Problem der flachen Oberfläche reduziert werden. In einem Experiment schnitt Schwartz ein Möbius-Band auf und stellte fest, dass es sich nicht um ein Parallelogramm, sondern um ein Trapez handelte. Endlich ist die 50 Jahre alte Frage beantwortet. Es erfordert Mut, ein seit langem bestehendes Problem zu lösen, und das ist Schwartz‘ Stärke in der Mathematik: Er arbeitet gerne an Problemen, die relativ einfach erscheinen, in Wirklichkeit aber schwierig sind. Er wird Probleme sehen, die früheren Forschern nicht aufgefallen sind. Referenzlink: https://www.scientificamerican.com/article/mathematicians-solve-50-year-old-moebius-strip-puzzle1/Das obige ist der detaillierte Inhalt vonWie lang muss das Papierband mindestens sein, um einen Möbiusstreifen herzustellen? 50 Jahre altes Rätsel gelöst. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!


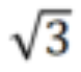 konstruiert werden können. Wenn das Armband beispielsweise 1 cm lang ist, muss seine Breite größer als
konstruiert werden können. Wenn das Armband beispielsweise 1 cm lang ist, muss seine Breite größer als  cm sein.
cm sein.