Heim >Backend-Entwicklung >C++ >Programm zur Berechnung der Oberfläche eines dreieckigen Prismas
Programm zur Berechnung der Oberfläche eines dreieckigen Prismas
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2023-09-22 17:57:091399Durchsuche
Sehen wir uns an, wie man ein Programm schreibt, um die Oberfläche eines dreieckigen Prismas zu berechnen.
Die Berechnung der Oberfläche eines dreieckigen Prismas mag sehr einfach erscheinen, Programmierer benötigen sie jedoch möglicherweise in vielen Bereichen. Nachfolgend sind einige häufige Szenarien aufgeführt –
3D-Grafik und Animation – Beim Erstellen von 3D-Modellen müssen Animatoren und Spieleentwickler möglicherweise die Oberfläche eines dreieckigen Prismas berechnen, um es in der virtuellen Welt richtig darzustellen.
Ingenieure und Architekten müssen möglicherweise die Oberfläche eines dreieckigen Prismas bestimmen, wenn sie Bauwerke wie Gebäude oder Brücken entwerfen.
Mathe und Geometrie – Programmierer, die an mathematisch oder geometriebezogenen Projekten arbeiten, müssen möglicherweise die Oberfläche eines dreieckigen Prismas als Teil ihres Algorithmus berechnen.
Physikalische Simulationen – Die Oberfläche eines dreieckigen Prismas kann eine Schlüsselmetrik in bestimmten physikalischen Simulationen sein, beispielsweise solchen, die Fluiddynamik oder elektromagnetische Felder betreffen.
Daher müssen wir als Programmierer in einigen Fällen möglicherweise die Oberfläche eines dreieckigen Prismas berechnen, um Genauigkeit und Präzision sicherzustellen.
Anleitung
Schauen Sie sich das Dreiecksprismendiagramm unten an und beobachten Sie das Bild, die Kanten und Flächen.
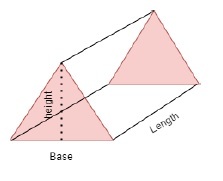
Die Formel zur Berechnung der Oberfläche eines dreieckigen Prismas lautet -
Oberfläche = $mathrm{(b:*:h):+:(L:*:(s1:+:s2:+:s3)) ;}$
wobei b = Basis
h=Höhe
L = Länge
s1=Seite 1 der Dreiecksfläche
s2=Seite 2 des Dreiecks
s3=Seite 3 des Dreiecks
Methode
Lassen Sie uns versuchen, die Schritte herauszufinden, die zum Schreiben eines Programms erforderlich sind. Mit anderen Worten: Schreiben wir einen Schritt-für-Schritt-Algorithmus.
-
Erhalten Sie die Eingabe der Variablen.
Hier müssen wir sechs Variablen eingeben, da wir ein dreieckiges Prisma verwenden. Die erforderlichen Variablen sind -
Basis – Die Basis eines Dreiecks
Höhe – Höhe des Dreiecks
Länge – Die Länge des Prismas
Seite1 – die Länge der ersten Seite des Dreiecks
Seite2 – die Länge der zweiten Seite des Dreiecks
Seite3 – Die Länge der dritten Seite des Dreiecks
Darüber hinaus benötigen wir auch Input für alle drei Seiten des Dreiecks –
-
Als nächstes berechnen wir die Fläche eines dreieckigen Prismas mithilfe der Formel -
Oberfläche = (Basis * Höhe) + (Länge * (Seite 1 + Seite 2 + Seite 3))
Hier gilt für eine dreieckige Fläche eines Prismas die Oberfläche = 0,5 * Grundfläche * Höhe. Daher gilt für zwei dreieckige Flächen die Gesamtoberfläche = Grundfläche * Höhe.
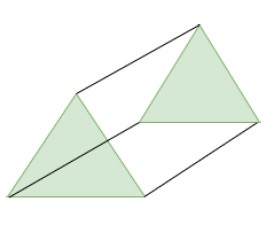
Länge*Umfang deckt die verbleibende Oberfläche ab.
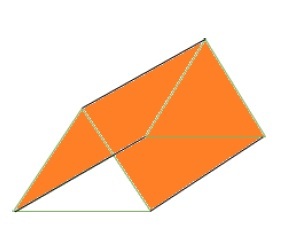
Abschließend drucken wir die berechnete Fläche aus -
Jetzt schreiben wir etwas Code.
Beispiel
C++-Programm zur Berechnung der Oberfläche eines dreieckigen Prismas
#include <iostream>
using namespace std;
int main() {
double base = 3, height = 6, length = 9, side1 = 3, side2 = 4, side3 = 5;
// calculate the surface area of the triangular prism
double surface_area_of_triangular_faces= base * height;
double perimeter = side1+side2+side3;
double surface_area_of_rectangular_faces= length * perimeter;
double surface_area_of_triangular_prism = surface_area_of_triangular_faces+ surface_area_of_rectangular_faces ;
// print the result
cout << "The surface area of the triangular prism is: " << surface_area_of_triangular_prism << endl;
return 0;
}
Ausgabe
The surface area of the triangular prism is: 126
Komplexität
Zeitkomplexität: O(1), da dieser Code unabhängig von der Eingabegröße eine feste Anzahl von Berechnungen durchführt.
Raumkomplexität: O(1), da der Code unabhängig von der Größe der Eingabe eine feste Anzahl von Variablen zum Speichern von Eingabewerten und Ergebnissen verwendet.
Fazit
In diesem Artikel versuchen wir, die Methode zur Berechnung der Oberfläche eines dreieckigen Prismas zu erklären, indem wir die Seiten der dreieckigen Fläche zusammen mit der Länge, der Basis und der Höhe als Eingabe verwenden. Ich hoffe, dieser Artikel hilft Ihnen, dieses Konzept besser zu erlernen.
Das obige ist der detaillierte Inhalt vonProgramm zur Berechnung der Oberfläche eines dreieckigen Prismas. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

