GPT-4 untersucht globale Probleme in 97 Dialogrunden und kommt zu dem Schluss, dass P≠NP

Für diejenigen, die auf dem Gebiet der wissenschaftlichen Forschung tätig sind, haben Sie mehr oder weniger vom P/NP-Problem gehört. Dieses Problem wurde vom Clay Institute of Mathematics in die Millennium Prize Problems aufgenommen. Alle bekannten Poincaré-Vermutungen, Riemann-Hypothese usw. sind enthalten. Und die Organisation hat Forschern, die das Problem lösen können, Preise in Millionenhöhe ausgelobt.

Das P/NP-Problem wurde erstmals 1971 von Stephen A. Cook und Leonid Levin vorgeschlagen. Im Laufe der Jahre haben sich viele Menschen der Erforschung dieses Problems gewidmet. Einige Leute sagen jedoch, dass es bei einer konservativen Schätzung von 100 Jahren dauern könnte, das P=NP-Problem zu lösen sind Fehler in diesen Beweisverfahren. Bisher konnte jedoch niemand eine eindeutige Antwort geben

Mit der Entwicklung der Technologie der künstlichen Intelligenz, insbesondere der schnellen Aktualisierung großer Sprachmodelle im vergangenen Jahr, haben Forscher begonnen, zu versuchen, die Technologie der künstlichen Intelligenz einzusetzen um einige globale Probleme zu lösen

Forscher von Microsoft Research, der Peking University, der Beihang University und anderen Institutionen haben vorgeschlagen, große Sprachmodelle (LLM) zu verwenden, um die Forschung zu P- und NP-Problemen zu verbessern und zu beschleunigen

Dieser Artikel schlägt A Der gemeinsame Rahmen, das sokratische Denken, wird verwendet, um LLM dazu zu bringen, tiefgründig nachzudenken und komplexe Probleme zu lösen. Auf der Grundlage dieses Frameworks ist LLM in der Lage, Probleme rekursiv zu entdecken, zu lösen und zu integrieren und gleichzeitig eine Selbstbewertung und Verbesserung durchzuführen Beweisen Sie das Modell und führen Sie in 97 Dialogrunden eine gründliche Argumentation durch, um zu der Schlussfolgerung zu gelangen, dass „P≠ NP“, was mit der Schlussfolgerung von (Xu und Zhou, 2023) übereinstimmt.

Bitte klicken Sie auf den folgenden Link, um das Papier anzuzeigen: https://arxiv.org/pdf/2309.05689.pdf

Der Hauptbeitrag dieses Papiers kann wie folgt zusammengefasst werden:

Integration von LLM als Mensch. Kooperationspartner, um komplexe wissenschaftliche Herausforderungen anzugehen und das „LLM for Science (LLM4Science)“-Paradigma vorzuschlagen.

Einführung eines Rahmenwerks namens „Socratic Reasoning“, um LLM dazu zu ermutigen, Deduktion, Transformation, Zerlegung und andere Methoden zu verwenden, um kritisches Denken anzuregen.

• Führen Sie eine Pilotstudie mit GPT-4 und dem Socratic Reasoning Framework durch, um P vs. NP-Probleme in der theoretischen Informatik zu lösen.
• GPT-4 generiert erfolgreich Beweismuster und führt in 97 Dialogrunden eine strenge Argumentation durch und kommt zu dem Schluss, dass P ≠ NP, im Einklang mit der jüngsten Arbeit von Xu und Zhou (2023).
• Diese Studie zeigt die potenzielle Fähigkeit von LLMs wie GPT-4, neues Wissen abzuleiten und komplexe Probleme auf Expertenebene in Zusammenarbeit mit Menschen zu untersuchen.
• In diesem Artikel wird LLM als allgemeiner Innovationsführer in allen Bereichen hervorgehoben, im Gegensatz zu früheren spezialisierten KI-Modellen, die auf bestimmte Aufgaben zugeschnitten sind.
• LLM Die Fähigkeit, natürliche und mathematische Sprache fließend zu verwenden, ist für interdisziplinäre Entdeckungen unerlässlich.
• Diese Arbeit zeigt, wie LLM als Partner genutzt werden kann, um den wissenschaftlichen Forschungsprozess in verschiedenen Bereichen zu verbessern und zu beschleunigen.
• Umgeschriebener Inhalt: In diesem Absatz wird erwähnt, dass sie das Rahmenwerk „Sokratisches Denken“ benannt haben, nachdem sie sich vom antiken griechischen Philosophen Sokrates inspirieren ließen. Sokrates sagte einmal: „Ich kann niemandem etwas beibringen. Ich kann ihn nur zum Nachdenken bringen.“ Und die allgemeine Designidee des Frameworks ist dieselbe. Es handelt sich um ein allgemeines Problemlösungsframework, das die Verwendung von LLM ermöglicht Navigieren Sie durch den Lösungsraum und gelangen Sie effizient zu Antworten
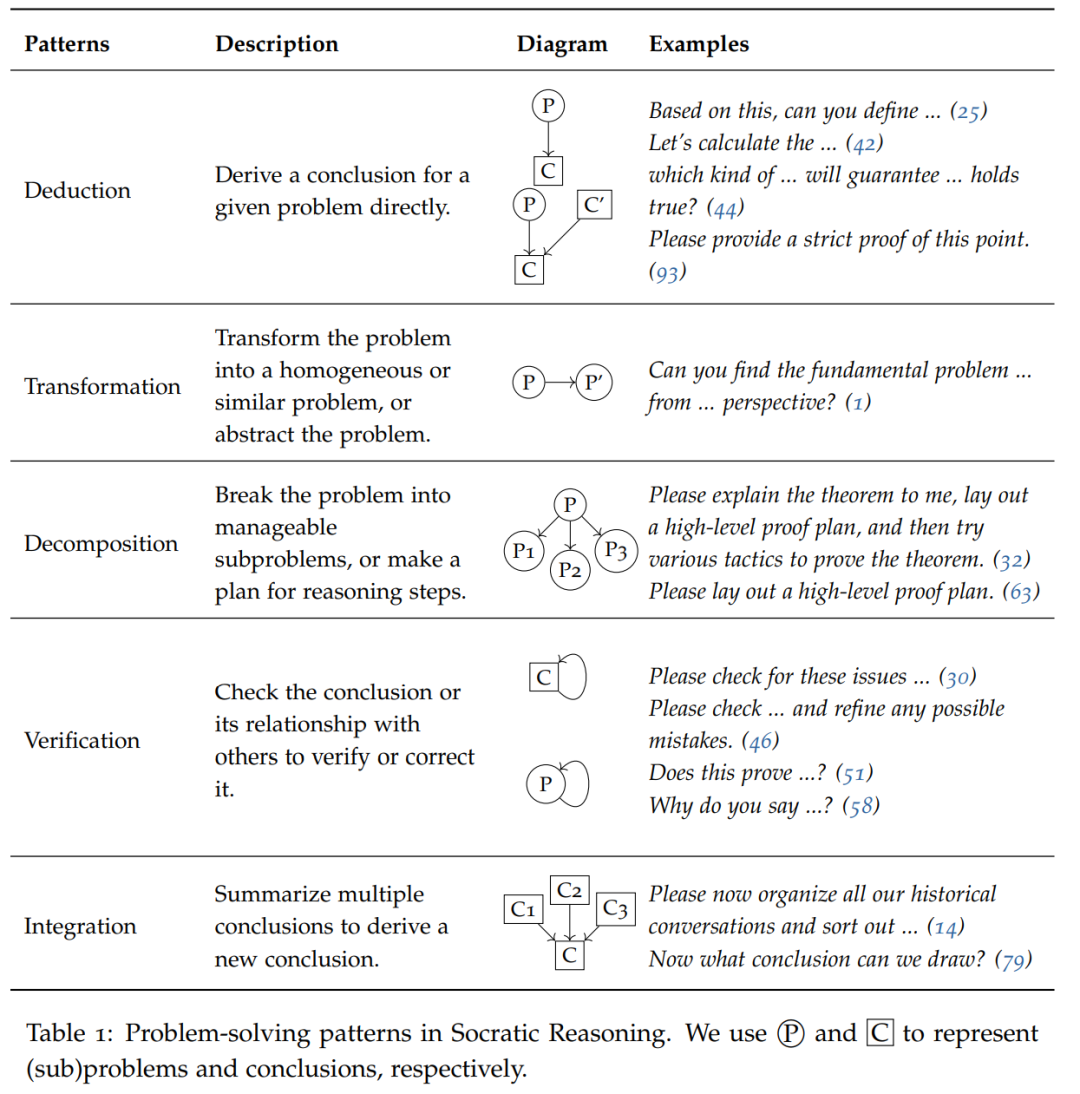
• Tabelle 1 listet die fünf Eingabeaufforderungsmodi des „sokratischen Denkens“ auf: Deduktion, Transformation, Zerlegung, Verifizierung und Fusion. Diese Muster werden verwendet, um neue Einsichten und Perspektiven zu entdecken, komplexe Probleme in Unterprobleme oder kleine Schritte zu zerlegen und sich durch Herausfordern und Reagieren auf Antworten zu verbessern. Bei kleineren Problemen (atomaren Problemen) kann LLM die Argumentationsergebnisse direkt liefern , wird ein deduktiver Modus verwendet (die Aufforderung lautet beispielsweise „Lassen Sie uns Schritt für Schritt denken ...“), um LLM dazu zu bringen, direkt Schlussfolgerungen zu ziehen.

Bei komplexeren Problemen erfordert dieser Artikel zunächst, dass LLM das Problem in ein neues Problem umwandelt oder es in mehrere Unterprobleme zerlegt. Diese Muster werden dann rekursiv ausgeführt, bis das atomare Ji-Problem erreicht ist.

Wenn neue Probleme auftreten oder neue Schlussfolgerungen gezogen werden, sollte der Verifizierungsmodus übernommen und die Selbstbewertungsfähigkeiten von LLM zur Verifizierung und Verbesserung genutzt werden

Schließlich erfordert der Fusionsmodus, dass das LLM Schlussfolgerungen basierend auf den Ergebnissen der Unterprobleme synthetisiert

Motivieren Sie das LLM rekursiv durch eine Reihe von Gesprächen, den oben genannten Prozess fortzusetzen, bis das Zielproblem gelöst ist

In dieser Arbeit bietet „Sucra „Socratic Reasoning“ einen systematischen Prompt-Rahmen für herausfordernde Probleme

Das Bild unten ist ein Beispiel für einen Dialog, der zur Lösung von P- vs. NP-Problemen in „Socratic Reasoning“ verwendet wird. In der Fallstudie wird die GPT-4-API verwendet. Darüber hinaus sortiert der Artikel die Prozesse basierend auf dem Rundenindex.

Während des Explorationsprozesses werden in diesem Artikel fünf verschiedene Rollen als Hilfsbeweiser vorgestellt, beispielsweise Mathematiker, die sich mit Wahrscheinlichkeitstheorie auskennen. Das Experiment führte insgesamt 97 Dialogrunden durch, aufgeteilt in 14 Runden davor und 83 Runden danach.

Zum Beispiel die Eingabeaufforderung der ersten Runde: Sie können P!=NP aus einer philosophischen Perspektive und nicht aus einer Computertheorie finden Perspektive. Das zugrunde liegende Problem?示 Im Folgenden sind weitere Tipps:

Der Dialog wird ständig unterzogen, und die letzte Runde des Dialogs lautet wie folgt: Schließlich Schlussfolgerung P

np

ist interessiert. Leser können sich das Originalpapier ansehen, um mehr zu erfahren.

Das obige ist der detaillierte Inhalt vonGPT-4 untersucht globale Probleme in 97 Dialogrunden und kommt zu dem Schluss, dass P≠NP. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!