Heim >Technologie-Peripheriegeräte >KI >Deep Thinking | Wo liegt die Leistungsgrenze großer Modelle?
Deep Thinking | Wo liegt die Leistungsgrenze großer Modelle?
- PHPznach vorne
- 2023-09-08 17:41:051339Durchsuche
Wenn wir über unbegrenzte Ressourcen wie unendliche Daten, unendliche Rechenleistung, unendliche Modelle, perfekte Optimierungsalgorithmen und Generalisierungsleistung verfügen, kann das resultierende vorab trainierte Modell dann zur Lösung aller Probleme verwendet werden?
Dies ist eine Frage, die allen große Sorgen bereitet, aber bestehende Theorien des maschinellen Lernens können sie nicht beantworten. Es hat nichts mit der Ausdrucksfähigkeitstheorie zu tun, da das Modell unendlich ist und die Ausdrucksfähigkeit von Natur aus unendlich ist. Es hat auch nichts mit der Optimierungs- und Generalisierungstheorie zu tun, da wir davon ausgehen, dass die Optimierungs- und Generalisierungsleistung des Algorithmus perfekt ist. Mit anderen Worten: Die Probleme der bisherigen theoretischen Forschung bestehen hier nicht mehr!
Heute werde ich Ihnen den Aufsatz „On the Power of Foundation Models“ vorstellen, den ich auf der ICML'2023 veröffentlicht habe, und eine Antwort aus der Perspektive der Kategorientheorie geben.
Was ist Kategorientheorie?
Wenn Sie kein Hauptfach Mathematik sind, sind Sie möglicherweise nicht mit der Kategorientheorie vertraut. Die Kategorientheorie wird als Mathematik der Mathematik bezeichnet und liefert eine Grundsprache für die moderne Mathematik. Fast alle modernen mathematischen Gebiete werden in der Sprache der Kategorientheorie beschrieben, wie etwa algebraische Topologie, algebraische Geometrie, algebraische Graphentheorie usw. Die Kategorietheorie ist die Untersuchung von Struktur und Beziehungen. Sie kann als natürliche Erweiterung der Mengenlehre angesehen werden: In der Mengenlehre enthält eine Menge mehrere verschiedene Elemente. In der Kategorientheorie erfassen wir nicht nur die Elemente, sondern auch die Beziehung zwischen Elementen .
Martin Kuppe hat einmal eine Karte der Mathematik gezeichnet und dabei die Kategorientheorie an die Spitze der Karte gesetzt, die auf allen Gebieten der Mathematik leuchtet:
Es gibt viele Einführungen in die Kategorientheorie im Internet. Lassen Sie uns kurz über einige sprechen Grundkonzepte hier:

Kategorientheoretische Perspektive des überwachten Lernens

In den letzten zehn Jahren haben Menschen viel Forschung rund um den Rahmen für überwachtes Lernen betrieben und viele schöne Schlussfolgerungen gezogen. Dieses Framework schränkt jedoch auch das Verständnis der Menschen für KI-Algorithmen ein, was es äußerst schwierig macht, große vorab trainierte Modelle zu verstehen. Beispielsweise ist es mit bestehenden Generalisierungstheorien schwierig, die modalübergreifenden Lernfähigkeiten von Modellen zu erklären.

Können wir diesen Funktor lernen, indem wir seine Eingabe- und Ausgabedaten abtasten?
Beachten Sie, dass wir in diesem Prozess die interne Struktur der beiden Kategorien X und Y nicht berücksichtigt haben. Tatsächlich werden beim überwachten Lernen keine Annahmen über die Struktur innerhalb der Kategorien getroffen, sodass davon ausgegangen werden kann, dass zwischen zwei Objekten innerhalb der beiden Kategorien keine Beziehung besteht. Daher können wir X und Y vollständig als zwei Mengen betrachten. Zu diesem Zeitpunkt sagt uns das berühmte No-Free-Lunch-Theorem der Generalisierungstheorie, dass es ohne zusätzliche Annahmen unmöglich ist, den Funktor von X nach Y zu lernen (es sei denn, es liegen umfangreiche Stichproben vor).

Auf den ersten Blick ist diese neue Perspektive nutzlos. Ob es um das Hinzufügen von Einschränkungen zu Kategorien oder um das Hinzufügen von Einschränkungen zu Funktoren geht, scheint es keinen wesentlichen Unterschied zu geben. Tatsächlich ähnelt die neue Perspektive eher einer kastrierten Version des traditionellen Rahmens: Sie erwähnt nicht einmal das Konzept der Verlustfunktion, das beim überwachten Lernen äußerst wichtig ist und nicht zur Analyse der Konvergenz- oder Generalisierungseigenschaften des Trainings verwendet werden kann Algorithmus. Wie sollen wir diese neue Perspektive verstehen?
Ich denke, die Kategorientheorie bietet eine Vogelperspektive. Es ist kein eigenständiger Ansatz und sollte auch nicht den ursprünglichen, spezifischeren Rahmen für überwachtes Lernen ersetzen oder zur Entwicklung besserer Algorithmen für überwachtes Lernen verwendet werden. Stattdessen handelt es sich bei Frameworks für überwachtes Lernen um deren „Untermodule“, Werkzeuge, die zur Lösung spezifischer Probleme eingesetzt werden können. Daher kümmert sich die Kategorientheorie nicht um Verlustfunktionen oder Optimierungsverfahren – diese sind eher Implementierungsdetails des Algorithmus. Es konzentriert sich mehr auf die Struktur von Kategorien und Funktoren und versucht zu verstehen, ob ein bestimmter Funktor lernbar ist. Diese Probleme sind in herkömmlichen Frameworks für überwachtes Lernen äußerst schwierig, werden jedoch in der Kategorieperspektive einfacher.
Kategorientheoretische Perspektive des selbstüberwachten Lernens
Aufgaben und Kategorien vor dem Training

Lassen Sie uns zunächst die Definition von Kategorien unter der Aufgabe vor dem Training klären. Wenn wir keine Vortrainingsaufgaben entwerfen, besteht tatsächlich keine Beziehung zwischen den Objekten in der Kategorie, aber nach dem Entwerfen der Vortrainingsaufgaben werden wir menschliches Vorwissen in Form von Aufgaben in die Kategorie einbringen. Und diese Strukturen werden zum Wissen des großen Modells.
Konkret:

Mit anderen Worten: Nachdem wir die Vortrainingsaufgabe für einen Datensatz definiert haben, definieren wir eine Kategorie, die die entsprechende Beziehungsstruktur enthält. Das Lernziel der Vortrainingsaufgabe besteht darin, dass das Modell diese Kategorie gut lernen kann. Konkret betrachten wir das Konzept eines idealen Modells.
Ideales Modell

Hier bedeutet „datenunabhängig“, dass vor dem Anzeigen der Daten vordefiniert ist; der Index f bedeutet jedoch, dass f und über Black-Box-Aufrufe These verwendet werden können zwei Funktionen. Mit anderen Worten: ist eine „einfache“ Funktion, kann aber auf die Fähigkeiten des Modells f zurückgreifen, um komplexere Beziehungen darzustellen. Dies ist möglicherweise nicht leicht zu verstehen. Nehmen wir als Vergleich einen Komprimierungsalgorithmus. Der Komprimierungsalgorithmus selbst kann datenabhängig sein, beispielsweise speziell für die Datenverteilung optimiert sein. Als datenunabhängige Funktion kann sie jedoch nicht auf die Datenverteilung zugreifen, kann jedoch den Komprimierungsalgorithmus aufrufen, um die Daten zu dekomprimieren, da der Vorgang „Aufrufen des Komprimierungsalgorithmus“ datenunabhängig ist.
Für verschiedene Aufgaben vor dem Training können wir verschiedene definieren:

Daher können wir sagen: Der Prozess des Lernens vor dem Training ist der Prozess, das ideale Modell f zu finden.
Auch wenn sicher ist, ist das ideale Modell per Definition nicht einzigartig. Theoretisch könnte Modell f superintelligent sein und alles tun können, ohne die Daten in C zu lernen. In diesem Fall können wir keine sinnvolle Aussage über die Fähigkeiten von f treffen. Deshalb sollten wir uns die andere Seite des Problems ansehen:
Gegeben eine Kategorie C, die durch eine vorab trainierte Aufgabe definiert ist, für jedes ideale f, welche Aufgaben kann es lösen?
Das ist die Kernfrage, die wir zu Beginn dieses Artikels beantworten wollen. Lassen Sie uns zunächst ein wichtiges Konzept vorstellen.
Yoneda-Einbettung
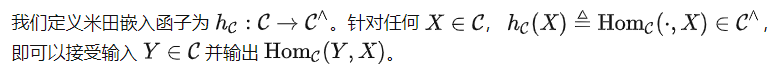

Es ist leicht zu zeigen, dass das schwächste ideale Modell ist, da bei anderen idealen Modellen f alle Beziehungen in auch in f enthalten sind. Gleichzeitig ist es auch das ultimative Ziel des Modelllernens vor dem Training ohne weitere zusätzliche Annahmen. Um unsere Kernfrage zu beantworten, gehen wir daher im Folgenden speziell auf ein.
Schnelle Abstimmung: Nur wer mehr sieht, kann mehr erfahren

Können Sie eine bestimmte Aufgabe T lösen? Um diese Frage zu beantworten, stellen wir zunächst einen der wichtigsten Sätze der Kategorientheorie vor.
Yoneda Lemma

Das heißt, kann T(X) mithilfe dieser beiden Darstellungen berechnen. Beachten Sie jedoch, dass die Aufgabenaufforderung P über statt über gesendet werden muss, was bedeutet, dass wir (P) anstelle von T als Eingabe für erhalten. Dies führt zu einer weiteren wichtigen Definition in der Kategorientheorie.
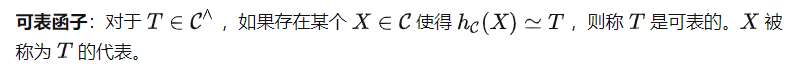
Basierend auf dieser Definition können wir den folgenden Satz erhalten (Beweis weggelassen).
Theorem 1 und Folgerung

Es ist erwähnenswert, dass einige Hinweise für den Optimierungsalgorithmus nicht unbedingt Objekte der Kategorie C sind, sondern möglicherweise Darstellungen im Merkmalsraum. Dieser Ansatz hat das Potenzial, komplexere Aufgaben als darstellbare Aufgaben zu unterstützen, die Verbesserung hängt jedoch von der Ausdruckskraft des Funktionsraums ab. Nachfolgend stellen wir eine einfache Folgerung von Satz 1 bereit.
Folge 1 Für die Vortrainingsaufgabe der Vorhersage des Bilddrehwinkels [4] kann die schnelle Optimierung komplexe nachgelagerte Aufgaben wie Segmentierung oder Klassifizierung nicht lösen.
Beweis: Die Vortrainingsaufgabe zur Vorhersage von Bilddrehwinkeln dreht ein gegebenes Bild um vier verschiedene Winkel: 0°, 90°, 180° und 270° und lässt das Modell Vorhersagen treffen. Daher ordnen die durch diese Vortrainingsaufgabe definierten Kategorien jedes Objekt einer Gruppe von 4 Elementen zu. Offensichtlich können Aufgaben wie Segmentierung oder Klassifizierung nicht durch solch einfache Objekte dargestellt werden.
Korollar 1 ist etwas kontraintuitiv, da in der Originalarbeit [4] erwähnt wurde, dass das mit dieser Methode erhaltene Modell teilweise nachgelagerte Aufgaben wie Klassifizierung oder Segmentierung lösen kann. In unserer Definition bedeutet das Lösen der Aufgabe jedoch, dass das Modell für jede Eingabe die richtige Ausgabe generieren sollte, sodass eine teilweise Richtigkeit nicht als Erfolg gewertet wird. Dies steht auch im Einklang mit der Frage, die am Anfang unseres Artikels gestellt wurde: Kann die vorab trainierte Aufgabe der Vorhersage von Bilddrehwinkeln mit der Unterstützung unbegrenzter Ressourcen zur Lösung komplexer nachgelagerter Aufgaben verwendet werden? Folgerung 1 gibt eine negative Antwort.
Feinabstimmung: Darstellung ohne Informationsverlust
Hinweise, dass die Fähigkeit zur Abstimmung begrenzt ist. Was ist also mit dem Feinabstimmungsalgorithmus? Basierend auf dem Yoneda-Funktorerweiterungssatz (siehe Satz 2.7.1 in [5]) können wir den folgenden Satz erhalten.
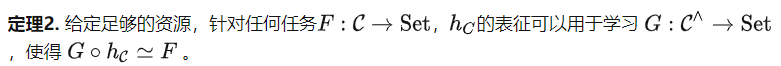
Theorem 2 berücksichtigt die nachgelagerten Aufgaben basierend auf der Struktur von C und nicht auf dem Dateninhalt im Datensatz. Daher weist die Kategorie, die durch die zuvor erwähnte Vortrainingsaufgabe zur Vorhersage des Winkels eines gedrehten Bildes definiert wurde, immer noch eine sehr einfache Gruppenstruktur auf. Doch nach Satz 2 können wir damit vielfältigere Aufgaben lösen. Beispielsweise können wir alle Objekte derselben Ausgabe zuordnen, was mit der Hinweisoptimierung nicht möglich ist. Satz 2 verdeutlicht die Bedeutung von Vortrainingsaufgaben, da bessere Vortrainingsaufgaben leistungsfähigere Kategorien C erzeugen und somit das Feinabstimmungspotenzial des Modells weiter verbessern.
Es gibt zwei häufige Missverständnisse zu Satz 2. Erstens: Selbst wenn Kategorie C eine große Menge an Informationen enthält, liefert Satz 2 nur eine grobe Obergrenze und besagt, dass alle Informationen in C aufzeichnet und das Potenzial hat, jede Aufgabe zu lösen, aber er besagt nicht, dass überhaupt welche vorhanden sind Ein Feinabstimmungsalgorithmus kann dieses Ziel erreichen. Zweitens sieht Satz 2 auf den ersten Blick wie eine überparametrisierte Theorie aus. Sie analysieren jedoch verschiedene Schritte des selbstüberwachten Lernens. Die parametrische Analyse ist der Schritt vor dem Training, was bedeutet, dass unter bestimmten Annahmen, solange das Modell groß genug und die Lernrate klein genug ist, die Optimierungs- und Generalisierungsfehler für die Aufgabe vor dem Training sehr gering sind. Satz 2 analysiert den Feinabstimmungsschritt nach dem Vortraining und besagt, dass dieser Schritt großes Potenzial hat.
Diskussion und Zusammenfassung
Überwachtes Lernen und selbstüberwachtes Lernen. Aus Sicht des maschinellen Lernens ist selbstüberwachtes Lernen immer noch eine Art überwachtes Lernen, aber die Art und Weise, Etiketten zu erhalten, ist cleverer. Aus kategorientheoretischer Sicht definiert selbstüberwachtes Lernen jedoch die Struktur innerhalb einer Kategorie, während überwachtes Lernen die Beziehung zwischen Kategorien definiert. Daher befinden sie sich in unterschiedlichen Teilen der Karte der künstlichen Intelligenz und tun völlig unterschiedliche Dinge.

Anwendbare Szenarien. Da zu Beginn dieses Artikels die Annahme unendlicher Ressourcen berücksichtigt wurde, denken viele Freunde vielleicht, dass diese Theorien nur im Nichts wirklich etabliert werden können. Dies ist nicht der Fall. In unserem eigentlichen Ableitungsprozess haben wir nur das ideale Modell und die vordefinierte Funktion berücksichtigt . Solange bestimmt ist, kann tatsächlich jedes vorab trainierte Modell f (auch in der zufälligen Initialisierungsphase) f(X) für die Eingabe XC berechnen und somit verwenden, um die Beziehung zwischen zwei Objekten zu berechnen. Mit anderen Worten, solange bestimmt ist, entspricht jedes vorab trainierte Modell einer Kategorie, und das Ziel des Vortrainings besteht lediglich darin, diese Kategorie kontinuierlich an der Kategorie auszurichten, die durch die Vortrainingsaufgabe definiert ist. Daher gilt unsere Theorie für jedes vorab trainierte Modell.
Kernformel. Viele Leute sagen, dass, wenn KI wirklich eine Reihe theoretischer Unterstützung hat, eine oder mehrere einfache und elegante Formeln dahinter stecken sollten. Ich denke, wenn wir eine kategorietheoretische Formel verwenden müssen, um die Fähigkeiten großer Modelle zu beschreiben, sollte es das sein, was wir zuvor erwähnt haben:
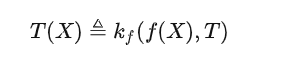
Für Freunde, die mit großen Modellen vertraut sind, nach einem gründlichen Verständnis der Bedeutung von Diese Formel, vielleicht denken Sie vielleicht, dass diese Formel Unsinn ist, aber sie drückt lediglich die Arbeitsweise des aktuellen großen Modells unter Verwendung einer relativ komplexen mathematischen Formel aus.
Aber das ist nicht der Fall. Die moderne Wissenschaft basiert auf Mathematik, und die moderne Mathematik basiert auf der Kategorientheorie. Der wichtigste Satz in der Kategorientheorie ist Yonedas Lemma. Die von mir geschriebene Formel zerlegt den Isomorphismus von Yoneda Lemma in eine asymmetrische Version, aber es ist genau die gleiche Methode zum Öffnen des großen Modells.
Ich glaube nicht, dass das ein Zufall ist. Wenn die Kategorientheorie verschiedene Zweige der modernen Mathematik beleuchten kann, kann sie auch den Weg nach vorne für die allgemeine künstliche Intelligenz beleuchten.
Dieser Artikel ist inspiriert von der langjährigen und engen Zusammenarbeit mit dem Qianfang-Team des Beijing Zhiyuan Artificial Intelligence Research Institute.

Originallink: https://mp.weixin.qq.com/s/bKf3JADjAveeJDjFzcDbkw
Das obige ist der detaillierte Inhalt vonDeep Thinking | Wo liegt die Leistungsgrenze großer Modelle?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Detaillierte Erläuterung der Verwendung des Orbit Controls-Plug-Ins (Orbit Control) durch Three.js zur Steuerung der Modellinteraktion
- Was ist das CSS-Box-Modell?
- Worauf bezieht sich das Python-IPO-Modell?
- Welche sind die am häufigsten verwendeten logischen Modelle in Datenbanken?
- Was sind die drei Datenmodelle der Datenbank?

