Multivariate Zeitreihenprognose: unabhängige Prognose oder gemeinsame Prognose?

Heute stelle ich einen Artikel vor, der im April dieses Jahres von der NTU veröffentlicht wurde. Darin werden hauptsächlich die Unterschiede in den Auswirkungen unabhängiger Vorhersagen (kanalunabhängig) und gemeinsamer Vorhersagen (kanalabhängig) bei multivariaten Zeitreihenvorhersageproblemen und die Gründe dafür erörtert und ihre Optimierungsmethode.

Papiertitel: The Capacity and Robustness Trade-off: Revisiting the Channel Independent Strategy for Multivariate Time Series Forecasting# 🎜🎜#

Download-Adresse: https://arxiv.org/pdf/2304.05206v1.pdf

1. Unabhängige Prognose und gemeinsame Prognose

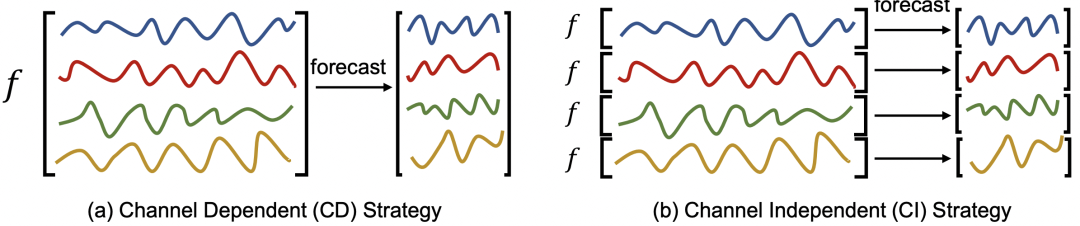
Mehrere Zeitreihen Bei Prognoseproblemen gibt es aus Sicht multivariabler Modellierungsmethoden zwei Arten: Die eine ist die kanalunabhängige Prognose (kanalunabhängig, CI), die sich auf die Behandlung multivariater Sequenzen als mehrere univariate Prognosen bezieht, und die andere ist die Eins ist eine gemeinsame Vorhersage (kanalabhängig, CD), die sich auf die gemeinsame Modellierung mehrerer Variablen und die Berücksichtigung der Beziehung zwischen den einzelnen Variablen bezieht. Der Unterschied zwischen den beiden ist wie unten dargestellt.

Die beiden Methoden haben ihre eigenen Eigenschaften: Die CI-Methode berücksichtigt nur eine einzige Variable, das Modell ist einfacher, die Obergrenze jedoch auch niedriger, weil Die Beziehung zwischen den einzelnen Sequenzen wird nicht berücksichtigt und einige Schlüsselinformationen gehen verloren, während die CD-Methode umfassendere Informationen berücksichtigt, aber das Modell ist auch komplexer.

2. Welche Methode ist besser?

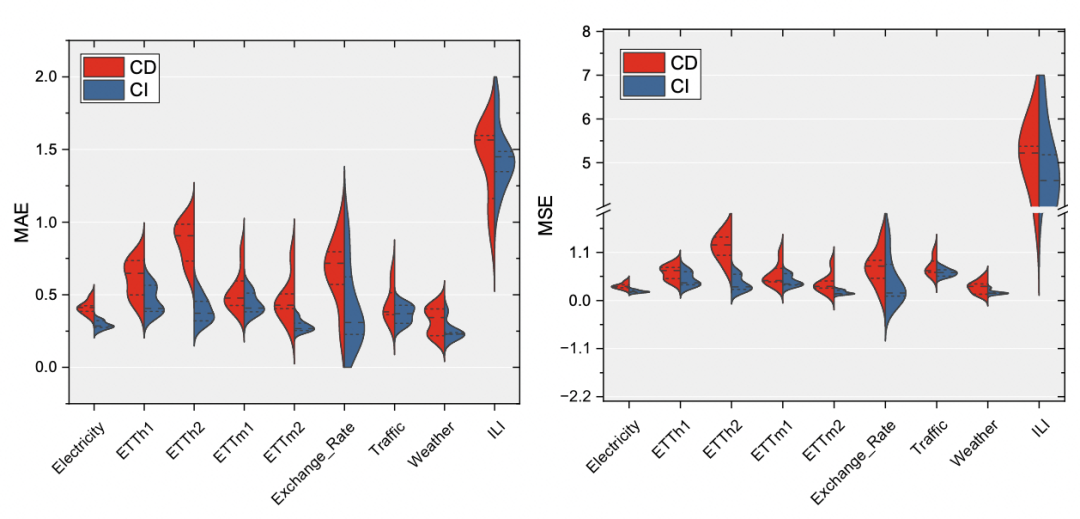
Führen Sie zunächst ein detailliertes Vergleichsexperiment durch und verwenden Sie lineare Modelle, um die Leistung der CI-Methode und der CD-Methode auf mehreren Ebenen zu beobachten Datensätze beeinflussen, um zu bestimmen, welche Methode besser ist. Eine der wichtigsten Schlussfolgerungen der Experimente in diesem Artikel ist, dass die CI-Methode bei den meisten Aufgaben eine bessere Leistung zeigt und eine stärkere Effektstabilität aufweist. Wie in der Abbildung unten zu sehen ist, sind die MAE-, MSE- und anderen Indikatoren von CI in jedem Datensatz grundsätzlich kleiner als die von CD, und die Fluktuation des Effekts ist ebenfalls geringer.

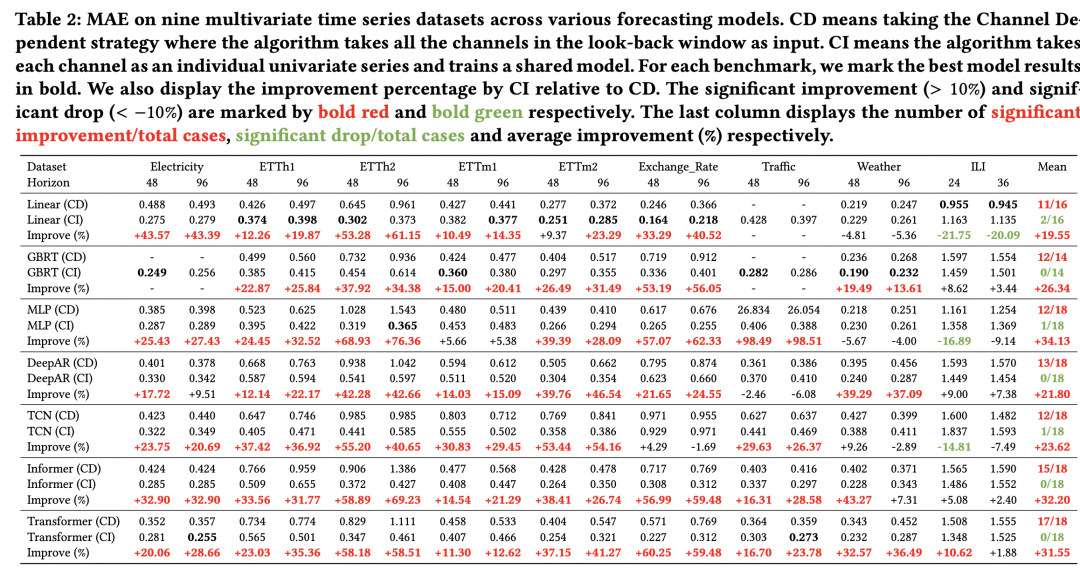
Wie aus den folgenden experimentellen Ergebnissen ersichtlich ist, ist CI in den meisten Vorhersagefensterlängen mit CD vergleichbar Datensatz werden die Effekte verbessert.

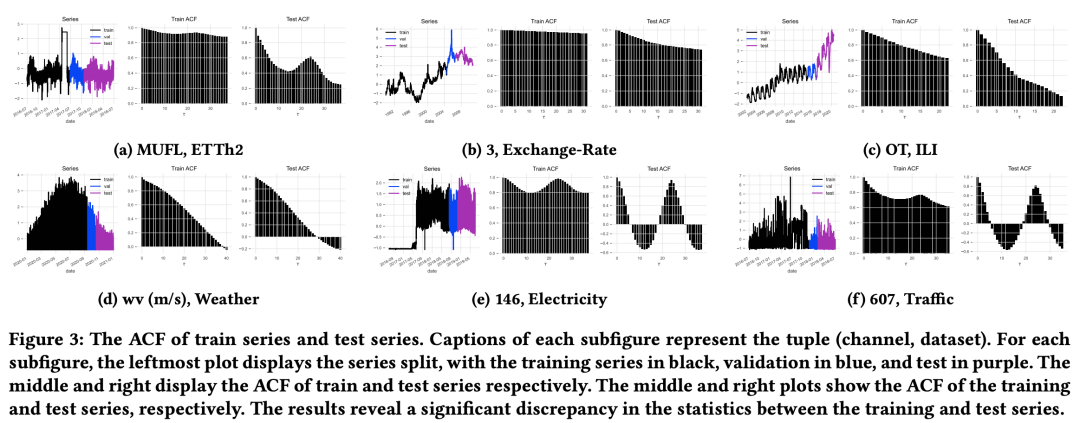
Warum ist die CI-Methode in der Praxis besser und stabiler als die CD? Der Artikel führte einige theoretische Beweise durch und die Kernschlussfolgerung ist, dass in realen Daten häufig eine Verteilungsdrift auftritt und die Verwendung von CI-Methoden dazu beitragen kann, dieses Problem zu lindern und die Modellverallgemeinerung zu verbessern. Das Bild unten zeigt die Verteilung des ACF (Autokorrelationskoeffizient, der die Beziehung zwischen zukünftigen Sequenzen und historischen Sequenzen widerspiegelt) jedes Datensatz-Zugsatzes und Testsatzes im Laufe der Zeit. Es ist ersichtlich, dass die Verteilungsdrift in verschiedenen Datensätzen weit verbreitet ist. Der ACF des Zugsatzes unterscheidet sich vom ACF des Testsatzes, d. h. die Beziehung zwischen der Geschichte und der zukünftigen Reihenfolge der beiden ist unterschiedlich.

Der Artikel beweist theoretisch, dass CI zur Minderung der Verteilungsdrift wirksam ist. Die Wahl zwischen CI und CD ist A Kompromiss zwischen Modellkapazität und Modellrobustheit. Obwohl das CD-Modell komplexer ist, reagiert es auch empfindlicher auf Verteilungsverschiebungen. Dies ähnelt tatsächlich der Beziehung zwischen Modellkapazität und Modellgeneralisierung. Je komplexer das Modell, desto genauer sind die Trainingssatzproben, zu denen das Modell passt, aber die Generalisierung ist schlecht. Sobald der Verteilungsunterschied zwischen dem Trainingssatz und dem Testsatz besteht ist groß, der Effekt wird schlimmer.

3. So optimieren Sie

In Bezug auf das Problem der CD-Modellierung werden in dem Artikel einige Optimierungsmethoden vorgeschlagen, die dazu beitragen können, dass das CD-Modell robuster wird.

Regularisierung: Führen Sie einen Regularisierungsverlust ein, verwenden Sie die Sequenz minus dem nächsten Abtastpunkt als historisches Sequenzeingabemodell für die Vorhersage und verwenden Sie Glättungsbeschränkungen, um vorherzusagen, dass die Ergebnisse von den Beobachtungen des nächsten Nachbarn abweichen groß, was die geschätzten Ergebnisse flacher macht; Zwei Matrizen niedriger Ordnung sind gleichbedeutend mit einer Reduzierung der Modellkapazität, einer Linderung von Überanpassungsproblemen und einer Verbesserung der Modellrobustheit: MAE wird anstelle von MSE verwendet Reduzieren Sie die Empfindlichkeit des Modells gegenüber Ausreißern.

Länge der historischen Eingabesequenz: Je länger die historische Eingabesequenz ist, desto geringer ist der Effekt Das Modell ist anfällig für den Einfluss der Verteilungsverschiebung. Beim CI-Modell kann eine Erhöhung der Länge der historischen Sequenz den Vorhersageeffekt relativ stabil verbessern.

4. Experimentelle Ergebnisse

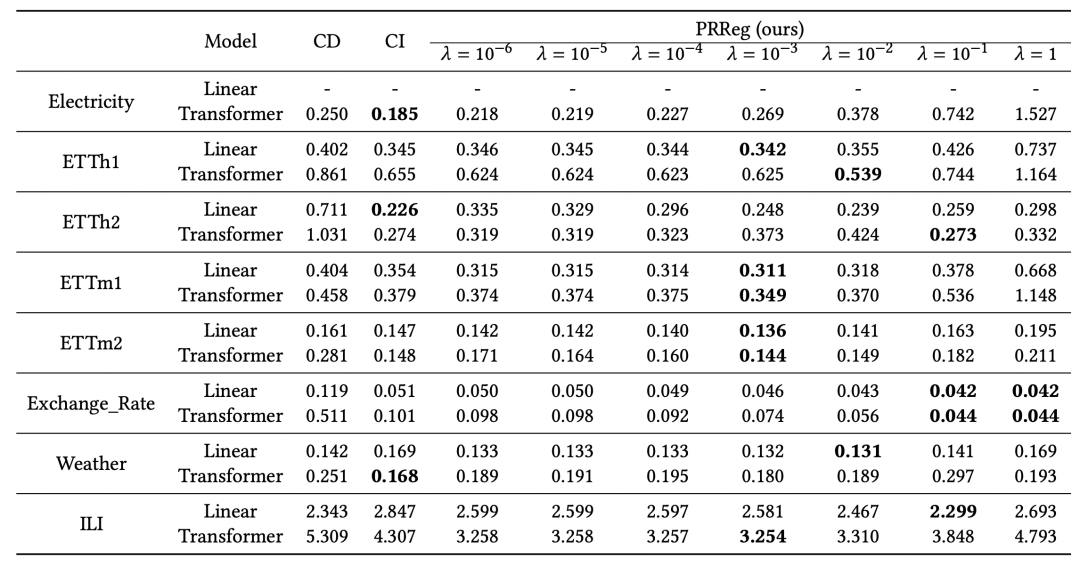
Die oben genannte Methode zur Verbesserung des CD-Modells wurde an mehreren Datensätzen getestet. Im Vergleich zu CD wurde eine relativ stabile Effektverbesserung erzielt, was darauf hinweist, dass die obige Methode die Robustheit des Multivariaten relativ effektiv verbessert Sequenzvorhersage. Experimentelle Ergebnisse zeigen, dass im Artikel auch Faktoren wie Low-Rank-Zerlegung, historische Fensterlänge und Verlustfunktionstyp aufgeführt sind, die den Effekt beeinflussen.

Das obige ist der detaillierte Inhalt vonMultivariate Zeitreihenprognose: unabhängige Prognose oder gemeinsame Prognose?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!