Heim >Technologie-Peripheriegeräte >KI >Ein Quantenproblem, für dessen Lösung 100.000 Gleichungen erforderlich waren, wurde von der KI ohne Einbußen bei der Genauigkeit auf nur vier komprimiert.
Ein Quantenproblem, für dessen Lösung 100.000 Gleichungen erforderlich waren, wurde von der KI ohne Einbußen bei der Genauigkeit auf nur vier komprimiert.
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2023-05-15 20:40:041341Durchsuche
Wechselwirkende Elektronen zeigen bei unterschiedlichen Energien und Temperaturen eine Vielzahl einzigartiger Phänomene. Wenn wir ihre Umgebung ändern, zeigen sie neue kollektive Verhaltensweisen, wie z. B. Spin, Paarungsschwankungen usw. Beim Umgang mit Elektronen gibt es jedoch immer noch viele Schwierigkeiten in diesen Phänomenen. Viele Forscher verwenden die Renormalization Group (RG), um dieses Problem zu lösen.
Im Kontext hochdimensionaler Daten hat das Aufkommen der Technologie des maschinellen Lernens (ML) und datengesteuerter Methoden großes Interesse bei Forschern der Quantenphysik geweckt. Bisher wurden ML-Ideen in der Interaktion von Elektronik eingesetzt Systeme.
In diesem Artikel komprimieren Physiker der Universität Bologna und anderer Institutionen mithilfe künstlicher Intelligenz ein Quantenproblem, für das bisher 100.000 Gleichungen erforderlich waren, in eine kleine Aufgabe mit nur 4 Gleichungen, die alle ohne Einbußen bei der Genauigkeit abgeschlossen werden. Die Forschung wurde kürzlich in Physical Review Letters veröffentlicht.
Papieradresse: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.129.136402
Domenico Di Sante, der Erstautor der Studie und Assistenzprofessor am Die Universität Bologna sagte: „Wir haben dieses riesige Projekt zusammengeführt und dann maschinelles Lernen genutzt, um es in Aufgaben zu verdichten, die man an einem Finger abzählen kann.“
Diese Studie beschäftigt sich mit der Frage, wie sich Elektronen verhalten, wenn sie sich über ein gitterartiges Kristallgitter bewegen. Wenn sich zwei Elektronen im selben Gitter befinden, kommt es nach bisheriger Erfahrung zu Wechselwirkungen. Dieses als Hubbard-Modell bekannte Phänomen ist ein idealisierter Aufbau einiger Materialien, der es Wissenschaftlern ermöglicht zu verstehen, wie das Elektronenverhalten Phasen der Materie erzeugt, beispielsweise die Supraleitung, in denen Elektronen ohne Widerstand durch das Material fließen. Das Modell kann auch als Testgelände für neue Methoden dienen, bevor sie auf komplexere Quantensysteme angewendet werden.
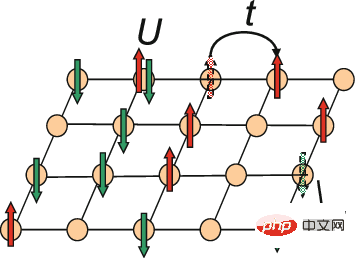
Schematische Darstellung des zweidimensionalen Hubbard-Modells
Das Hubbard-Modell scheint einfach, aber selbst die Verwendung modernster Rechenmethoden zur Verarbeitung einer kleinen Anzahl von Elektronen erfordert eine leistungsstarke Rechenleistung. Denn wenn Elektronen interagieren, verschränken sie sich quantenmechanisch: Selbst wenn die Elektronen im Gitter weit voneinander entfernt sind, können die beiden Elektronen nicht unabhängig voneinander behandelt werden, sodass Physiker sich mit allen gleichzeitig befassen müssen, anstatt mit einem einzigen zu arbeiten Elektron nach dem anderen. Je mehr Elektronen vorhanden sind, desto größer ist die quantenmechanische Verschränkung und der Rechenaufwand nimmt exponentiell zu.
Eine gängige Methode zur Untersuchung von Quantensystemen ist die Renormierungsgruppe. Als mathematisches Gerät verwenden Physiker es, um das Verhalten eines Systems zu beobachten, beispielsweise das Hubbard-Modell. Leider zeichnet eine Renormierungsgruppe alle möglichen Kopplungen zwischen Elektronen auf, die Tausende, Hunderttausende oder sogar Millionen unabhängiger Gleichungen enthalten können, die gelöst werden müssen. Darüber hinaus sind die Gleichungen komplex: Jede Gleichung repräsentiert ein Paar wechselwirkender Elektronen.
Das Di Sante-Team wollte wissen, ob es ein maschinelles Lerntool namens neuronales Netzwerk verwenden könnte, um Renormierungsgruppen besser handhabbar zu machen.
Bei neuronalen Netzen verwenden die Forscher zunächst Verfahren des maschinellen Lernens, um Verbindungen zur Renormierungsgruppe in voller Größe herzustellen. Anschließend passt das neuronale Netzwerk die Stärke dieser Verbindungen an, bis es einen kleinen Satz von Gleichungen findet, die generiert werden der gleiche Gleichungssatz wie das Original, die gleiche Lösung für sehr große Renormierungsgruppen. Am Ende haben wir vier Gleichungen, und obwohl es nur vier sind, spiegelt die Ausgabe des Programms die Physik von Hubbards Modell wider.
Di Sante sagte: „Ein neuronales Netzwerk ist im Wesentlichen eine Maschine, die verborgene Muster entdecken kann, und dieses Ergebnis hat unsere Erwartungen übertroffen.“ mehrere Wochen bis zur Fertigstellung. Die gute Nachricht ist, dass ihr Programm jetzt läuft und mit ein paar Optimierungen andere Probleme lösen kann, ohne bei Null anfangen zu müssen.
Als er über zukünftige Forschungsrichtungen sprach, sagte Di Sante, dass es notwendig sei, zu überprüfen, wie effektiv die neue Methode bei komplexeren Quantensystemen sei. Darüber hinaus gibt es laut Di Sante große Möglichkeiten, die Technik in anderen Bereichen in Bezug auf Renormierungsgruppen wie der Kosmologie und den Neurowissenschaften einzusetzen.
Papierübersicht
Wir führen eine datengesteuerte Dimensionsreduktion an einer skalenabhängigen Vier-Scheitelpunkt-Funktion durch, die die Fließeigenschaften der funktionellen Renormierungsgruppe (fRG) des vielfach untersuchten zweidimensionalen t-t'-Hubbard-Modells für quadratische Kristalle beschreibt. Sie zeigen, dass eine Deep-Learning-Architektur, die auf einem neuronalen regulären Differentialgleichungslöser (NODE) in einem niedrigdimensionalen latenten Raum basiert, die fRG-Dynamik, die verschiedene magnetische und d-Wellen-Supraleitungszustände des Hubbard-Modells beschreibt, effizient lernen kann.
Die Forscher schlugen außerdem eine Analyse der dynamischen Modenzerlegung vor, die bestätigen kann, dass einige wenige Moden tatsächlich ausreichen, um die fRG-Dynamik zu erfassen. Die Forschung zeigt die Möglichkeit, mithilfe künstlicher Intelligenz kompakte Darstellungen relevanter Elektronen-Vier-Scheitelpunkt-Funktionen zu extrahieren. Dies ist das wichtigste Ziel für die erfolgreiche Implementierung modernster Methoden der Quantenfeldtheorie und die Lösung von Vielelektronenproblemen. Das Grundobjekt in
fRG ist die Scheitelpunktfunktion V(k_1, k_2, k_3), die im Prinzip als Funktion berechnet und gespeichert werden muss, die aus drei kontinuierlichen Impulsvariablen besteht. Durch die Untersuchung spezifischer theoretischer Muster wird angenommen, dass das zweidimensionale Hubbard-Modell für Kuprate und eine Vielzahl organischer Leiter relevant ist. Wir zeigen, dass niedrigerdimensionale Darstellungen den fRG-Fluss hochdimensionaler Scheitelpunktfunktionen erfassen können. 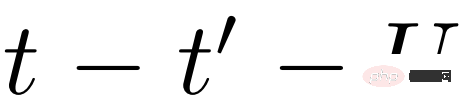
Der fRG-Grundzustand des Hubbard-Modells. Der vom Forscher berücksichtigte mikroskopische Hamiltonoperator ist in der folgenden Formel (1) dargestellt. Die 2-Teilchen-Eigenschaften des
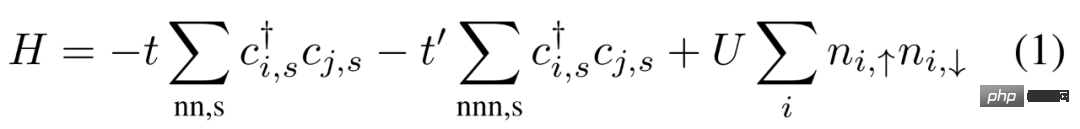
Hubbard-Modells werden durch ein Einschleifen-fRG-Schema des Temperaturflusses untersucht, wobei der RG-Fluss von 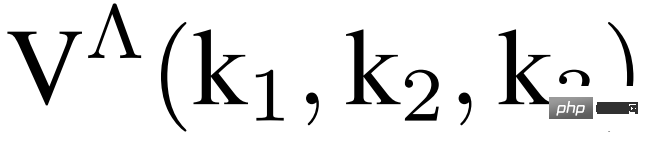 in der folgenden Gleichung (2) dargestellt ist.
in der folgenden Gleichung (2) dargestellt ist.
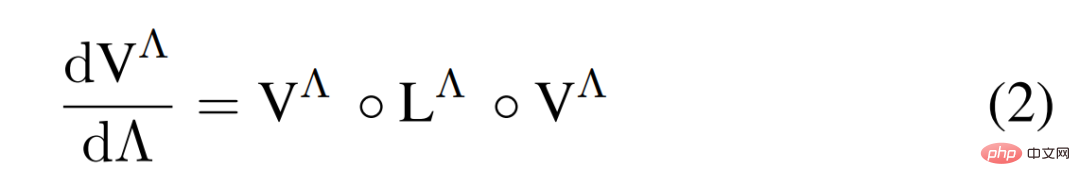
Abbildung 1 a) unten ist eine grafische Darstellung der Ein-Ring-fRG-Flussgleichung der 2-Teilchen-Scheitelpunktfunktion V^Λ.
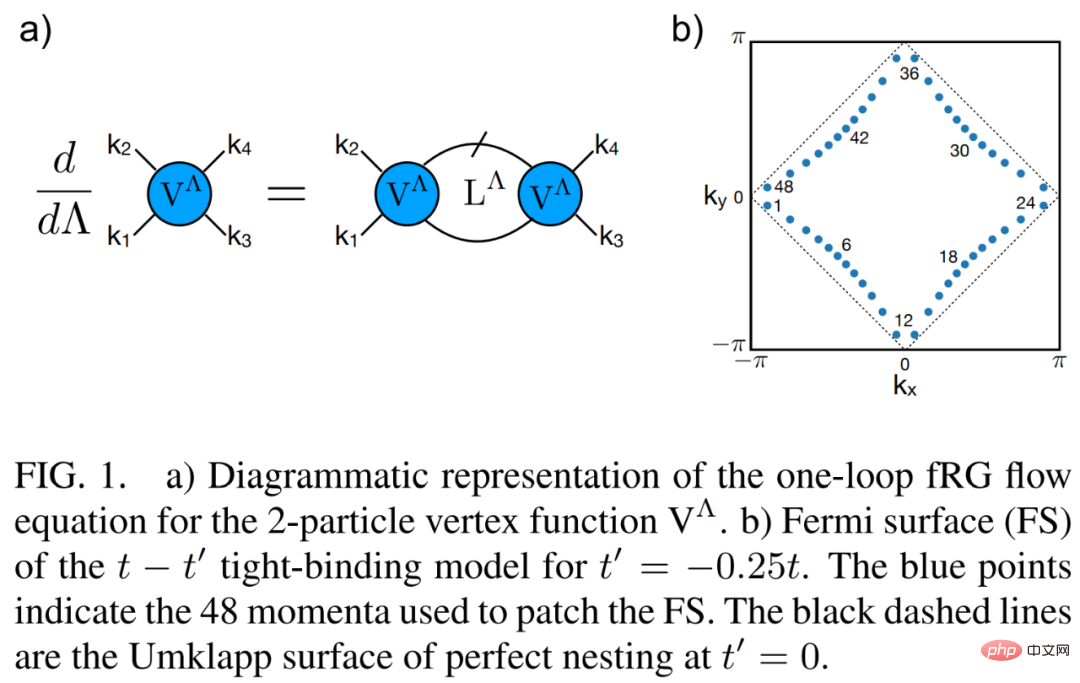
Als nächstes schauen wir uns Deep Learning fRG an. Wie in Abbildung 2 b) unten gezeigt, stellten die Forscher durch die Untersuchung der 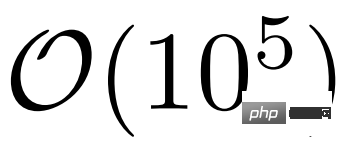 -Kopplung der 2-Teilchen-Scheitelpunktfunktion vor der Tendenz des fRG-Flusses zu starker Kopplung und der Ein-Ring-Näherungszerlegung fest, dass viele von ihnen entweder im bleiben Randzustand oder wird nicht relevant.
-Kopplung der 2-Teilchen-Scheitelpunktfunktion vor der Tendenz des fRG-Flusses zu starker Kopplung und der Ein-Ring-Näherungszerlegung fest, dass viele von ihnen entweder im bleiben Randzustand oder wird nicht relevant.
Die Forscher implementieren ein flexibles Schema zur Dimensionsreduktion, das auf der parametrisierten NODE-Architektur basiert und für aktuelle hochdimensionale Probleme geeignet ist. Diese Methode ist in Abbildung 2 a) unten dargestellt und konzentriert sich auf tiefe neuronale Netze.
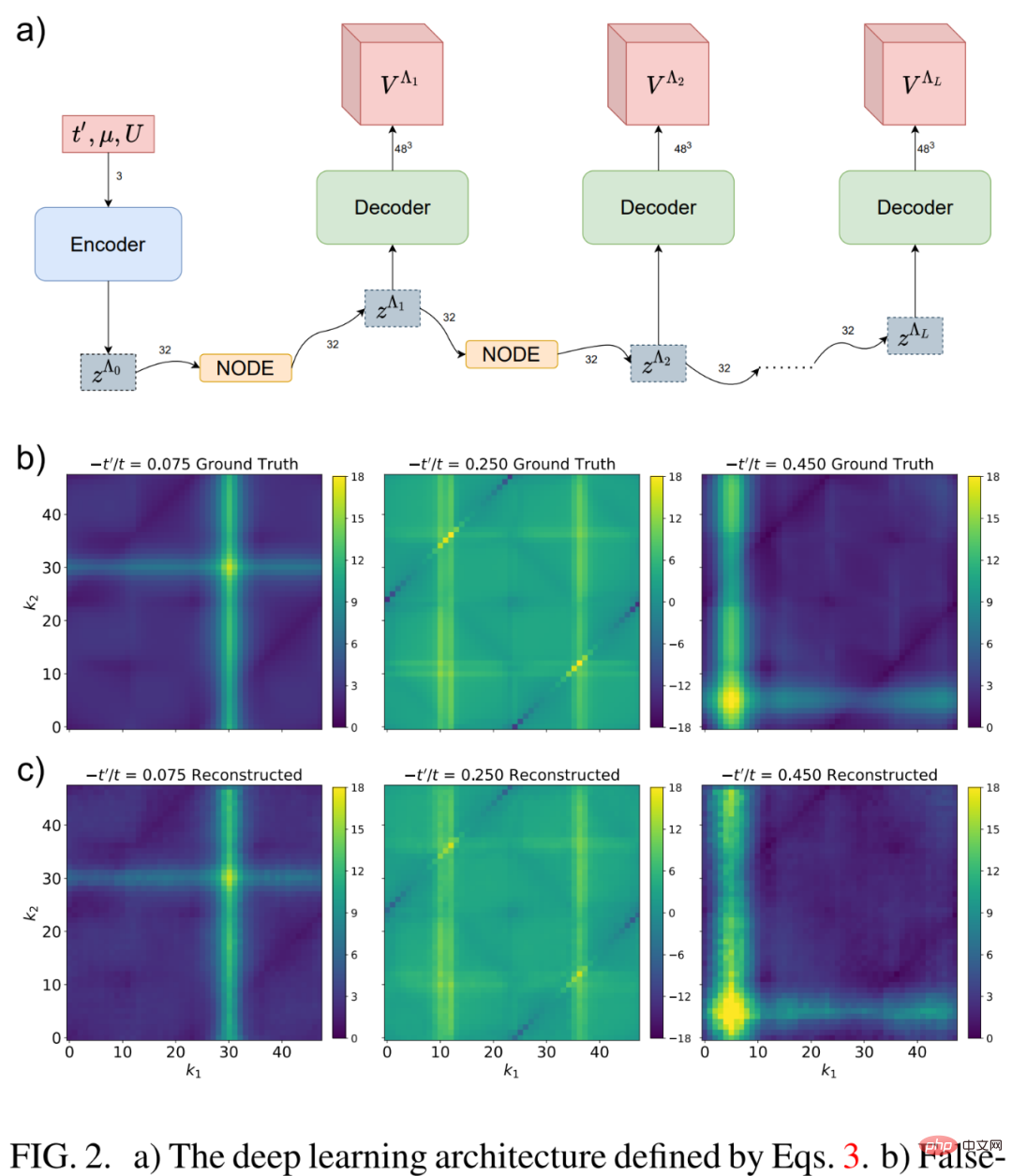
Abbildung 3 unten zeigt drei statistisch hochkorrelierte latente Raumdarstellungen z als gelernte Merkmale des neuronalen Netzwerks NODE während der fRG-Dynamik des latenten Raums.
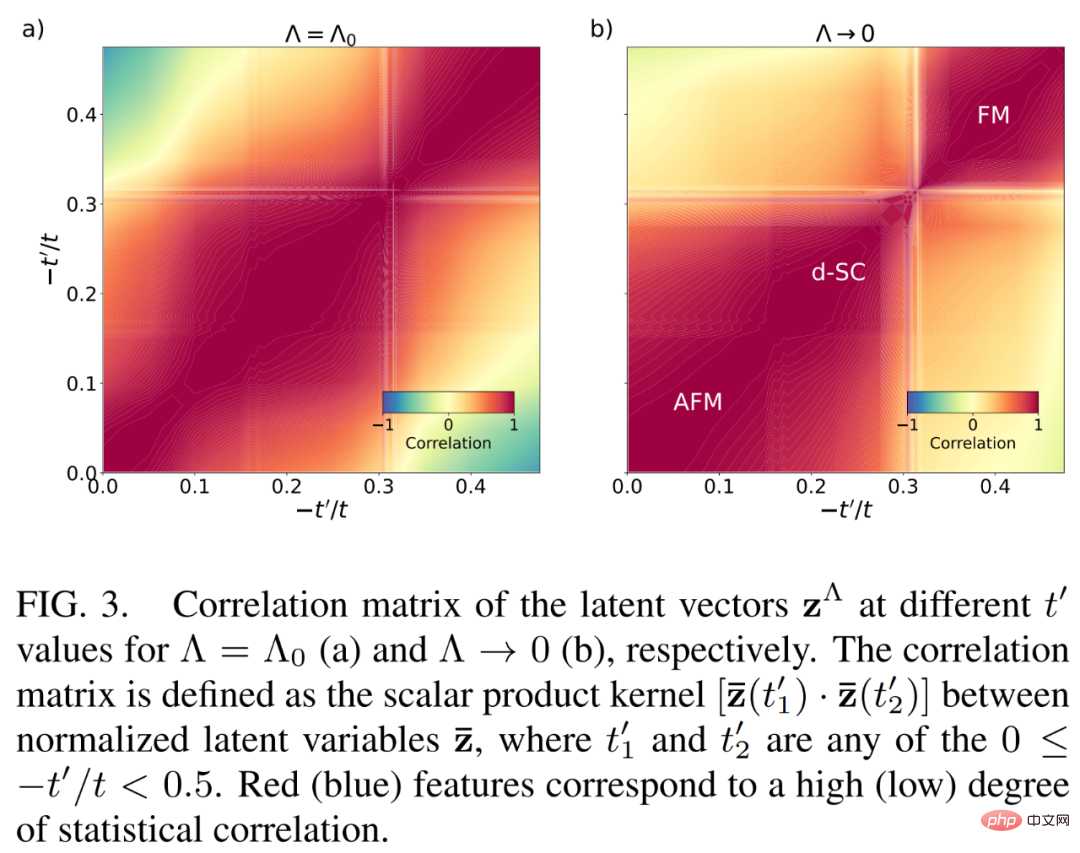
Weitere Einzelheiten finden Sie im Originalpapier.
Das obige ist der detaillierte Inhalt vonEin Quantenproblem, für dessen Lösung 100.000 Gleichungen erforderlich waren, wurde von der KI ohne Einbußen bei der Genauigkeit auf nur vier komprimiert.. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Technologietrends, die Sie im Jahr 2023 im Auge behalten sollten
- Wie künstliche Intelligenz Rechenzentrumsteams neue Alltagsaufgaben beschert
- Können künstliche Intelligenz oder Automatisierung das Problem der geringen Energieeffizienz in Gebäuden lösen?
- OpenAI-Mitbegründer im Interview mit Huang Renxun: Die Argumentationsfähigkeiten von GPT-4 haben noch nicht die Erwartungen erfüllt
- Dank der OpenAI-Technologie übertrifft Bing von Microsoft Google im Suchverkehr

