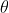Heim >Backend-Entwicklung >Python-Tutorial >So implementieren Sie einen Gradientenabstieg, um die logistische Regression in Python zu lösen
So implementieren Sie einen Gradientenabstieg, um die logistische Regression in Python zu lösen
- 王林nach vorne
- 2023-05-12 15:13:061483Durchsuche
Lineare Regression
1. Die Definition der linearen Regressionsfunktion
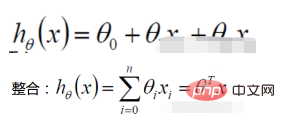
Wahrscheinlichkeitsfunktion: gegebener gemeinsamer Stichprobenwert Zufallsfunktion : Welche Art von Parametern sind in Kombination mit unseren Daten genau die wahren Werte
2. Lineare Regressionswahrscheinlichkeitsfunktion
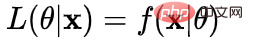
Log-Wahrscheinlichkeit: 
3. Lineare Regressionszielfunktion
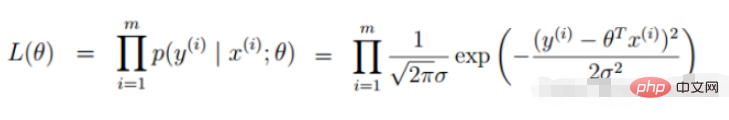 (Fehlerausdruck, unser Ziel ist es, den Fehler zwischen dem wahren Wert und dem vorhergesagten Wert zu minimieren )
(Fehlerausdruck, unser Ziel ist es, den Fehler zwischen dem wahren Wert und dem vorhergesagten Wert zu minimieren )
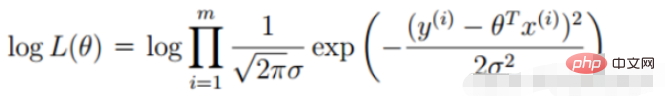 (Die Ableitung ist 0, um den Extremwert zu erhalten, und die Parameter der Funktion werden erhalten)
(Die Ableitung ist 0, um den Extremwert zu erhalten, und die Parameter der Funktion werden erhalten)
Logistische Regression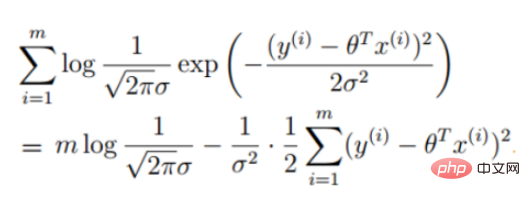
1. Logistische Regressionsfunktion
wird
eingeführt eine Gradientenabstiegsaufgabe, und die logistische Regressionszielfunktion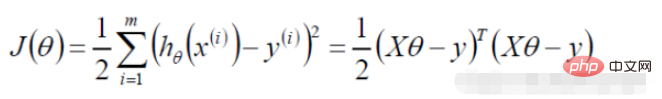 wird durch die Gradientenabstiegsmethode gelöst
wird durch die Gradientenabstiegsmethode gelöst
Mein Verständnis besteht darin, die Parameter durch Ableitung zu aktualisieren, nach Erreichen einer bestimmten Bedingung anzuhalten und eine annähernd optimale Lösung zu erhalten
Code-Implementierung
Sigmoidfunktion
def sigmoid(z): return 1 / (1 + np.exp(-z))
Vorhersagefunktion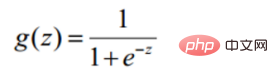
def model(X, theta):
return sigmoid(np.dot(X, theta.T))Zielfunktion
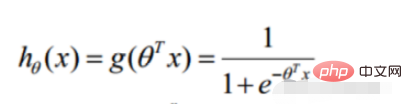
def cost(X, y, theta):
left = np.multiply(-y, np.log(model(X, theta)))
right = np.multiply(1 - y, np.log(1 - model(X, theta)))
return np.sum(left - right) / (len(X))Gradient
def gradient(X, y, theta):
grad = np.zeros(theta.shape)
error = (model(X, theta)- y).ravel()
for j in range(len(theta.ravel())): #for each parmeter
term = np.multiply(error, X[:,j])
grad[0, j] = np.sum(term) / len(X)
return gradStrategie zum Stoppen des Gradientenabstiegs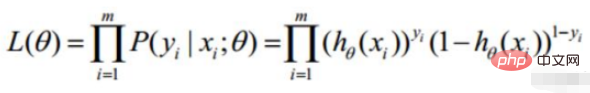
STOP_ITER = 0
STOP_COST = 1
STOP_GRAD = 2
def stopCriterion(type, value, threshold):
# 设定三种不同的停止策略
if type == STOP_ITER: # 设定迭代次数
return value > threshold
elif type == STOP_COST: # 根据损失值停止
return abs(value[-1] - value[-2]) < threshold
elif type == STOP_GRAD: # 根据梯度变化停止
return np.linalg.norm(value) < thresholdBeispielumbildung import numpy.random
#洗牌
def shuffleData(data):
np.random.shuffle(data)
cols = data.shape[1]
X = data[:, 0:cols-1]
y = data[:, cols-1:]
return X, yGradientenabstiegslösung def descent(data, theta, batchSize, stopType, thresh, alpha):
# 梯度下降求解
init_time = time.time()
i = 0 # 迭代次数
k = 0 # batch
X, y = shuffleData(data)
grad = np.zeros(theta.shape) # 计算的梯度
costs = [cost(X, y, theta)] # 损失值
while True:
grad = gradient(X[k:k + batchSize], y[k:k + batchSize], theta)
k += batchSize # 取batch数量个数据
if k >= n:
k = 0
X, y = shuffleData(data) # 重新洗牌
theta = theta - alpha * grad # 参数更新
costs.append(cost(X, y, theta)) # 计算新的损失
i += 1
if stopType == STOP_ITER:
value = i
elif stopType == STOP_COST:
value = costs
elif stopType == STOP_GRAD:
value = grad
if stopCriterion(stopType, value, thresh): break
return theta, i - 1, costs, grad, time.time() - init_time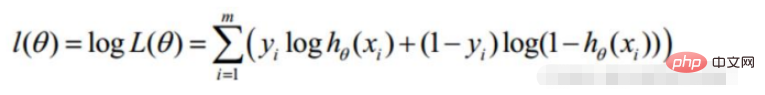 Vollständiger Code
Vollständiger Code import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import os
import numpy.random
import time
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def model(X, theta):
return sigmoid(np.dot(X, theta.T))
def cost(X, y, theta):
left = np.multiply(-y, np.log(model(X, theta)))
right = np.multiply(1 - y, np.log(1 - model(X, theta)))
return np.sum(left - right) / (len(X))
def gradient(X, y, theta):
grad = np.zeros(theta.shape)
error = (model(X, theta) - y).ravel()
for j in range(len(theta.ravel())): # for each parmeter
term = np.multiply(error, X[:, j])
grad[0, j] = np.sum(term) / len(X)
return grad
STOP_ITER = 0
STOP_COST = 1
STOP_GRAD = 2
def stopCriterion(type, value, threshold):
# 设定三种不同的停止策略
if type == STOP_ITER: # 设定迭代次数
return value > threshold
elif type == STOP_COST: # 根据损失值停止
return abs(value[-1] - value[-2]) < threshold
elif type == STOP_GRAD: # 根据梯度变化停止
return np.linalg.norm(value) < threshold
# 洗牌
def shuffleData(data):
np.random.shuffle(data)
cols = data.shape[1]
X = data[:, 0:cols - 1]
y = data[:, cols - 1:]
return X, y
def descent(data, theta, batchSize, stopType, thresh, alpha):
# 梯度下降求解
init_time = time.time()
i = 0 # 迭代次数
k = 0 # batch
X, y = shuffleData(data)
grad = np.zeros(theta.shape) # 计算的梯度
costs = [cost(X, y, theta)] # 损失值
while True:
grad = gradient(X[k:k + batchSize], y[k:k + batchSize], theta)
k += batchSize # 取batch数量个数据
if k >= n:
k = 0
X, y = shuffleData(data) # 重新洗牌
theta = theta - alpha * grad # 参数更新
costs.append(cost(X, y, theta)) # 计算新的损失
i += 1
if stopType == STOP_ITER:
value = i
elif stopType == STOP_COST:
value = costs
elif stopType == STOP_GRAD:
value = grad
if stopCriterion(stopType, value, thresh): break
return theta, i - 1, costs, grad, time.time() - init_time
def runExpe(data, theta, batchSize, stopType, thresh, alpha):
# import pdb
# pdb.set_trace()
theta, iter, costs, grad, dur = descent(data, theta, batchSize, stopType, thresh, alpha)
name = "Original" if (data[:, 1] > 2).sum() > 1 else "Scaled"
name += " data - learning rate: {} - ".format(alpha)
if batchSize == n:
strDescType = "Gradient" # 批量梯度下降
elif batchSize == 1:
strDescType = "Stochastic" # 随机梯度下降
else:
strDescType = "Mini-batch ({})".format(batchSize) # 小批量梯度下降
name += strDescType + " descent - Stop: "
if stopType == STOP_ITER:
strStop = "{} iterations".format(thresh)
elif stopType == STOP_COST:
strStop = "costs change < {}".format(thresh)
else:
strStop = "gradient norm < {}".format(thresh)
name += strStop
print("***{}\nTheta: {} - Iter: {} - Last cost: {:03.2f} - Duration: {:03.2f}s".format(
name, theta, iter, costs[-1], dur))
fig, ax = plt.subplots(figsize=(12, 4))
ax.plot(np.arange(len(costs)), costs, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title(name.upper() + ' - Error vs. Iteration')
return theta
path = 'data' + os.sep + 'LogiReg_data.txt'
pdData = pd.read_csv(path, header=None, names=['Exam 1', 'Exam 2', 'Admitted'])
positive = pdData[pdData['Admitted'] == 1]
negative = pdData[pdData['Admitted'] == 0]
# 画图观察样本情况
fig, ax = plt.subplots(figsize=(10, 5))
ax.scatter(positive['Exam 1'], positive['Exam 2'], s=30, c='b', marker='o', label='Admitted')
ax.scatter(negative['Exam 1'], negative['Exam 2'], s=30, c='r', marker='x', label='Not Admitted')
ax.legend()
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')
pdData.insert(0, 'Ones', 1)
# 划分训练数据与标签
orig_data = pdData.values
cols = orig_data.shape[1]
X = orig_data[:, 0:cols - 1]
y = orig_data[:, cols - 1:cols]
# 设置初始参数0
theta = np.zeros([1, 3])
# 选择的梯度下降方法是基于所有样本的
n = 100
runExpe(orig_data, theta, n, STOP_ITER, thresh=5000, alpha=0.000001)
runExpe(orig_data, theta, n, STOP_COST, thresh=0.000001, alpha=0.001)
runExpe(orig_data, theta, n, STOP_GRAD, thresh=0.05, alpha=0.001)
runExpe(orig_data, theta, 1, STOP_ITER, thresh=5000, alpha=0.001)
runExpe(orig_data, theta, 1, STOP_ITER, thresh=15000, alpha=0.000002)
runExpe(orig_data, theta, 16, STOP_ITER, thresh=15000, alpha=0.001)
from sklearn import preprocessing as pp
# 数据预处理
scaled_data = orig_data.copy()
scaled_data[:, 1:3] = pp.scale(orig_data[:, 1:3])
runExpe(scaled_data, theta, n, STOP_ITER, thresh=5000, alpha=0.001)
runExpe(scaled_data, theta, n, STOP_GRAD, thresh=0.02, alpha=0.001)
theta = runExpe(scaled_data, theta, 1, STOP_GRAD, thresh=0.002 / 5, alpha=0.001)
runExpe(scaled_data, theta, 16, STOP_GRAD, thresh=0.002 * 2, alpha=0.001)
# 设定阈值
def predict(X, theta):
return [1 if x >= 0.5 else 0 for x in model(X, theta)]
# 计算精度
scaled_X = scaled_data[:, :3]
y = scaled_data[:, 3]
predictions = predict(scaled_X, theta)
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y)]
accuracy = (sum(map(int, correct)) % len(correct))
print('accuracy = {0}%'.format(accuracy))Vorteile und Nachteile der logistischen Regression
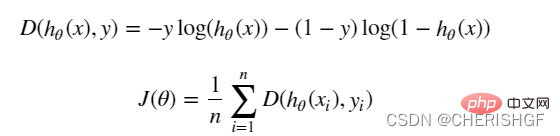
Es beansprucht nur wenig Ressourcen, insbesondere Speicher. Denn nur die Merkmalswerte jeder Dimension müssen gespeichert werden.
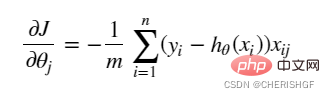
Es ist schwierig, mit dem Problem des Datenungleichgewichts umzugehen. Beispiel: Wenn wir uns mit einem Problem befassen, bei dem positive und negative Stichproben sehr unausgeglichen sind, beispielsweise wenn das Verhältnis von positiven und negativen Stichproben 10.000:1 beträgt, können wir auch den Wert der Verlustfunktion festlegen kleiner. Als Klassifikator ist seine Fähigkeit, positive und negative Proben zu unterscheiden, jedoch nicht sehr gut.
Die Verarbeitung nichtlinearer Daten ist problematischer. Die logistische Regression kann ohne Einführung anderer Methoden nur linear trennbare Daten oder darüber hinaus binäre Klassifizierungsprobleme verarbeiten.
Die logistische Regression selbst kann keine Features filtern. Manchmal verwenden wir gbdt zum Filtern von Features und verwenden dann die logistische Regression.
Das obige ist der detaillierte Inhalt vonSo implementieren Sie einen Gradientenabstieg, um die logistische Regression in Python zu lösen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!