So implementieren Sie den Kruskal-Algorithmus in Java

Einführung

Es gibt einen anderen Algorithmus zum Erstellen eines minimalen Spannbaums, nämlich den Kruskal-Algorithmus: Der Graph G=(V, E) sei ein ungerichteter verbundener gewichteter Graph, V={1,2,...n}; der minimale Spannbaum Baum T = (V, TE), der Anfangszustand des Baumes ist ein nicht zusammenhängender Graph mit nur n Knoten und keinen Kanten T = (V, {}). Kruskals Algorithmus behandelt diese n Knoten als n isoliert verbundene Filialen. Zuerst werden alle Kanten entsprechend ihrer Gewichtung von klein nach groß sortiert. Wenn dann die Anzahl der in T auszuwählenden Kanten kleiner als n-1 ist, wird eine gierige Auswahl wie folgt durchgeführt: Wählen Sie die Kante (i, j) aus. mit dem kleinsten Gewicht in der Kantenmenge E), wenn das Hinzufügen von Kante (i, j) zur Menge TE keinen Zyklus erzeugt, dann füge Kante (i, j) zur Kantenmenge TE hinzu, das heißt, verwende Kante (i , j) um die beiden Zweige zu einem verbundenen Zweig zusammenzuführen; andernfalls fahren Sie mit der Auswahl der nächstkürzesten Kante fort. Löschen Sie die Kante (i, j) aus der Menge E und setzen Sie die obige gierige Auswahl fort, bis sich alle Knoten in T auf demselben verbundenen Zweig befinden. Zu diesem Zeitpunkt bilden die ausgewählten n-1 Kanten genau einen minimalen Spannbaum T des Graphen G.

Der Kruskal-Algorithmus verwendet eine sehr intelligente Methode, die darin besteht, Kreise mithilfe von Mengen zu vermeiden. Wenn der Startpunkt und der Endpunkt der ausgewählten zu verbindenden Kante beide in der T-Menge liegen, kann daraus geschlossen werden, dass eine Schleife gebildet wird. und die beiden geänderten Knoten können nicht zur gleichen Menge gehören.

Algorithmusschritte

1 Initialisierung. Sortieren Sie alle Kanten in aufsteigender Reihenfolge ihres Gewichts und initialisieren Sie jede Knotensatznummer mit ihrer eigenen Nummer.

2 Wählen Sie die Kante (u, v) mit dem kleinsten Gewicht in der sortierten Reihenfolge aus.

3 Wenn die Knoten u und v zu zwei verschiedenen verbundenen Zweigen gehören, fügen Sie die Kante (u, v) zur Kantenmenge TE hinzu und führen Sie die beiden verbundenen Zweige zusammen.

4 Wenn die Anzahl der ausgewählten Kanten weniger als n-1 beträgt, fahren Sie mit Schritt 2 fort, andernfalls endet der Algorithmus.

1. Das konstruierte Bild

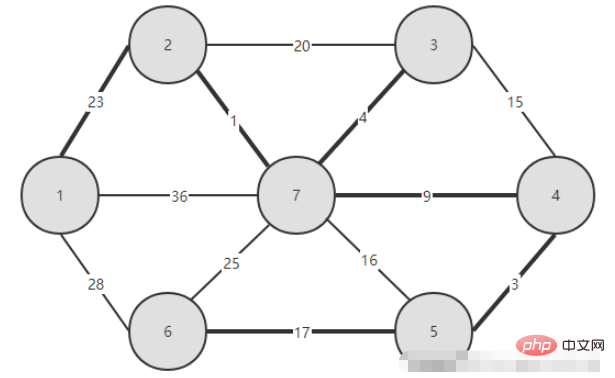
2. Code

package graph.kruskal;
 
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Scanner;
 
public class Kruskal {
    static final int N = 100;
    static int fa[] = new int[N];
    static int n;
    static int m;
 
    static Edge e[] = new Edge[N * N];
    static List<Edge> edgeList = new ArrayList();
 
    static {
        for (int i = 0; i < e.length; i++) {
            e[i] = new Edge();
        }
    }
 
    // 初始化集合号为自身
    static void Init(int n) {
        for (int i = 1; i <= n; i++)
            fa[i] = i;
    }
 
    // 合并
    static int Merge(int a, int b) {
        int p = fa[a];
        int q = fa[b];
        if (p == q) return 0;
        for (int i = 1; i <= n; i++) { // 检查所有结点，把集合号是 q 的改为 p
            if (fa[i] == q)
                fa[i] = p; // a 的集合号赋值给 b 集合号
        }
        return 1;
    }
 
    // 求最小生成树
    static int Kruskal(int n) {
        int ans = 0;
        Collections.sort(edgeList);
        for (int i = 0; i < m; i++)
            if (Merge(edgeList.get(i).u, edgeList.get(i).v) == 1) {
                ans += edgeList.get(i).w;
                n--;
                if (n == 1)//n-1次合并算法结束
                    return ans;
            }
        return 0;
    }
 
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();
        m = scanner.nextInt();
        Init(n);
        for (int i = 1; i <= m; i++) {
            e[i].u = scanner.nextInt();
            e[i].v = scanner.nextInt();
            e[i].w = scanner.nextInt();
            edgeList.add(e[i]);
        }
        System.out.println("最小的花费是：" + Kruskal(n));
    }
}
 
class Edge implements Comparable {
    int u;
    int w;
    int v;
 
    @Override
    public int compareTo(Object o) {
        if (this.w > ((Edge) o).w) {
            return 1;
        } else if (this.w == ((Edge) o).w) {
            return 0;
        } else {
            return -1;
        }
    }
}

Grün ist die Eingabe und Weiß ist die Ausgabe.

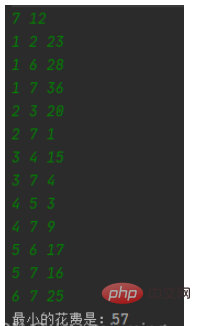
Das obige ist der detaillierte Inhalt vonSo implementieren Sie den Kruskal-Algorithmus in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!