Verfolgen Sie nicht blind große Modelle und häufen Sie Rechenleistung an! Shen Xiangyang, Cao Ying und Ma Yi schlugen zwei Grundprinzipien für das Verständnis von KI vor: Sparsamkeit und Selbstkonsistenz

​In den letzten zwei Jahren sind große Modelle, die „mit großer Leistung (Rechenleistung) Wunder geschehen lassen“, zum Trend geworden, den die meisten Forscher auf dem Gebiet der künstlichen Intelligenz verfolgen. Die dahinter stehenden enormen Rechenkosten und Ressourcenverbrauchsprobleme wurden jedoch allmählich deutlich. Einige Wissenschaftler haben begonnen, sich ernsthaft mit großen Modellen zu befassen und aktiv nach Lösungen zu suchen. Neue Forschungsergebnisse zeigen, dass das Erreichen einer hervorragenden Leistung von KI-Modellen nicht unbedingt von der Heap-Rechenleistung und der Heap-Größe abhängt.

Deep Learning boomt seit zehn Jahren. Man muss sagen, dass seine Chancen und Engpässe in diesen zehn Jahren der Forschung und Praxis viel Aufmerksamkeit und Diskussion erregt haben.

Unter diesen sind die Black-Box-Eigenschaften von Deep Learning (mangelnde Interpretierbarkeit) und „wundersame Ergebnisse mit großem Aufwand“ (Modellparameter werden immer größer und die Anforderungen an die Rechenleistung steigen) die auffälligste Engpassdimension Auch der Rechenaufwand wird immer höher. Darüber hinaus gibt es auch Probleme wie unzureichende Modellstabilität und Sicherheitslücken.

Im Wesentlichen werden diese Probleme teilweise durch die „Open-Loop“-Systemnatur tiefer neuronaler Netze verursacht. Um den „Fluch“ der B-Seite des Deep Learning zu brechen, reicht es möglicherweise nicht aus, einfach den Modellmaßstab und die Rechenleistung zu erweitern. Stattdessen müssen wir die Quelle anhand der Grundprinzipien künstlicher Intelligenzsysteme ermitteln eine neue Perspektive (z. B. geschlossener Regelkreis) „Intelligenz“ verstehen.

Am 12. Juli veröffentlichten drei bekannte chinesische Wissenschaftler auf dem Gebiet der künstlichen Intelligenz, Ma Yi, Cao Ying und Shen Xiangyang, gemeinsam einen Artikel auf arXiv mit dem Titel „On the Principles of Parsimony and Self-Consistency for the Emergence“. of Intelligence“ schlägt einen neuen Rahmen zum Verständnis tiefer Netzwerke vor: die komprimierende Closed-Loop-Transkription.

Dieses Framework enthält zwei Prinzipien: Sparsamkeit und Selbstkonsistenz, die jeweils dem „Lernen“ und dem „Lernen“ im Lernprozess des KI-Modells entsprechen. Sie gelten als die beiden wichtigsten Grundlagen stellen künstliche/natürliche Intelligenz dar und haben im Bereich der künstlichen Intelligenzforschung im In- und Ausland große Aufmerksamkeit erregt.

Link zum Papier:

https://arxiv.org/pdf/2207.04630.pdf

Drei Wissenschaftler glauben, dass echte Intelligenz zwei Eigenschaften haben muss, eine ist Erklärbarkeit und die andere ist Interpretierbarkeit. ist Berechenbarkeit.

Der Fortschritt der künstlichen Intelligenz basierte jedoch im letzten Jahrzehnt hauptsächlich auf Deep-Learning-Methoden, die „Brute-Force“-Trainingsmodelle verwenden. In diesem Fall kann das KI-Modell jedoch auch funktionale Module für die Wahrnehmung erhalten und Entscheidungsfindung. Die erlernten Merkmalsdarstellungen sind oft implizit und schwer zu interpretieren.

Darüber hinaus hat die ausschließliche Verwendung einer großen Menge an Rechenleistung zum Trainieren des Modells auch dazu geführt, dass der Maßstab des KI-Modells weiter zunimmt, die Rechenkosten weiter steigen und bei Landeanwendungen viele Probleme aufgetreten sind. B. ein neuronaler Kollaps, der zu einem Mangel an Vielfalt in der Natur der erlernten Darstellungen führt, ein Moduskollaps, der zu einem Mangel an Stabilität beim Training führt, eine schlechte Modellempfindlichkeit gegenüber Anpassungsfähigkeit und katastrophales Vergessen usw.

Drei Wissenschaftler glauben, dass das oben genannte Problem auftritt, weil in aktuellen tiefen Netzwerken das Training diskriminierender Modelle zur Klassifizierung und generativer Modelle zur Stichprobe oder Wiedergabe in den meisten Fällen getrennt ist. Bei solchen Modellen handelt es sich typischerweise um Open-Loop-Systeme, die eine umfassende Schulung durch Supervision oder Selbstsupervision erfordern. Wiener und andere haben schon lange herausgefunden, dass ein solches Open-Loop-System Fehler in Vorhersagen nicht automatisch korrigieren und sich auch nicht an Veränderungen in der Umgebung anpassen kann.

Daher befürworten sie die Einführung eines „Closed-Loop-Feedbacks“ in das Steuerungssystem, damit das System lernen kann, Fehler selbstständig zu beheben. In dieser Studie fanden sie auch heraus, dass das System durch die Verwendung des diskriminierenden Modells und des generativen Modells zur Bildung eines vollständigen geschlossenen Regelkreises unabhängig (ohne externe Aufsicht) lernen kann und effizienter, stabiler und anpassungsfähiger ist.

Bildunterschrift: Von links nach rechts sind Shun Xiangyang (Präsidentenprofessor von Hongkong, China und Shenzhen, ausländischer Akademiker der National Academy of Engineering, ehemaliger Global Executive Vice President von Microsoft), Cao Ying (Akademiker der National Academy of Sciences, University of California, Berkeley) (Professor an der University of California, Berkeley) und Ma Yi (Professor an der University of California, Berkeley).

Zwei Prinzipien der Intelligenz: Einfachheit und Selbstkonsistenz

In dieser Arbeit schlugen drei Wissenschaftler zwei Grundprinzipien vor, um die Zusammensetzung künstlicher Intelligenz zu erklären, nämlich Einfachheit und Selbstkonsistenz (auch bekannt als „Selbstkonsistenz“) ") und am Beispiel der visuellen Bilddatenmodellierung wird ein komprimiertes Transkriptionsframework mit geschlossenem Regelkreis aus den ersten Prinzipien der Sparsamkeit und Selbstkonsistenz abgeleitet.

Einfachheit

Die sogenannte Einfachheit ist „was man lernen sollte“. Das Prinzip der intelligenten Sparsamkeit erfordert, dass Systeme auf recheneffiziente Weise kompakte und strukturierte Darstellungen erhalten. Das heißt, intelligente Systeme können jedes strukturierte Modell verwenden, das die Welt beschreibt, solange sie nützliche Strukturen in sensorischen Daten der realen Welt einfach und effizient simulieren können. Das System sollte in der Lage sein, die Qualität eines Lernmodells anhand grundlegender, universeller, einfach zu berechnender und zu optimierender Metriken genau und effizient zu bewerten.

Am Beispiel der visuellen Datenmodellierung versucht das Parsimony-Prinzip, eine (nichtlineare) Transformation f zu finden, um folgende Ziele zu erreichen:

#🎜 🎜#Komprimierung: Abbildung hochdimensionaler sensorischer Daten x auf niedrigdimensionale Darstellung z;

Linearisierung: Abbildung jedes Objekttyps, der auf einer nichtlinearen Untermannigfaltigkeit verteilt ist, auf einen linearen Unterraum;

# 🎜 🎜#Skarifizierung: Abbildung verschiedener Klassen in Unterräume mit unabhängiger oder maximal inkohärenter Basis.

Das heißt, reale Daten, die sich möglicherweise auf einer Reihe niedrigdimensionaler Untermannigfaltigkeiten in einem hochdimensionalen Raum befinden, werden in einen unabhängigen niedrigdimensionalen linearen Unterraum umgewandelt Serie. Dieses Modell wird als „lineare diskriminative Darstellung“ (LDR) bezeichnet. Der Komprimierungsprozess ist in Abbildung 2 dargestellt:

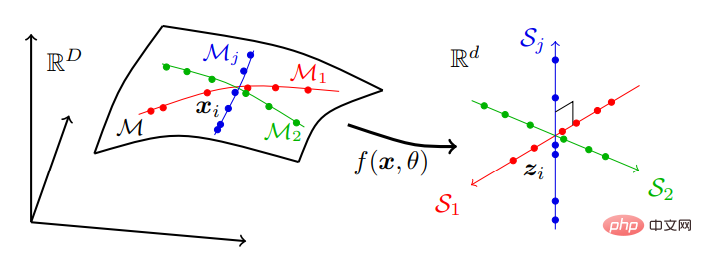Abbildung 2: Suchen Sie nach linearen und diskriminierenden Darstellungen Ordnen Sie hochdimensionale sensorische Daten, die typischerweise über viele nichtlineare niedrigdimensionale Untermannigfaltigkeiten verteilt sind, einem Satz unabhängiger linearer Unterräume mit den gleichen Abmessungen wie die Untermannigfaltigkeiten zu.

In der Familie der LDR-Modelle gibt es ein intrinsisches Maß an Sparsamkeit. Das heißt, wir können bei einem gegebenen LDR das gesamte „Volumen“ berechnen, das von allen Features über alle Unterräume überspannt wird, und die Summe des „Volumens“, das von Features jeder Kategorie überspannt wird. Das Verhältnis zwischen diesen beiden Volumina gibt dann ein natürliches Maß dafür, wie gut das LDR-Modell ist (größer ist oft besser).

Gemäß der Informationstheorie kann das Volumen einer Verteilung anhand ihrer Ratenverzerrung gemessen werden.

Eine Arbeit von Ma Yis Team aus dem Jahr 2022 „ReduNet: A White-box Deep Network from the Principle of Maximizing Rate Reduction“ zeigt, dass bei Verwendung der Gaußschen Ratenverzerrung Funktion und Wählen Sie ein allgemeines tiefes Netzwerk (z. B. ResNet), um die Abbildung f(x, θ) durch Minimierung der Codierungsrate zu modellieren.

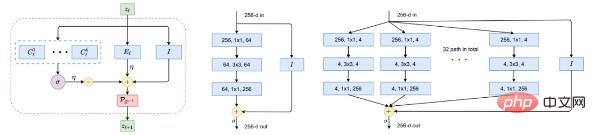Abbildung 5: Bausteine ​​der nichtlinearen Abbildung f. Links: Eine Schicht von ReduNet als Iteration des projizierten Gradientenanstiegs, die genau aus expandierenden oder komprimierenden linearen Operatoren, nichtlinearem Softmax, Skip-Verbindungen und Normalisierung besteht. Mitte und rechts in der Abbildung: eine Schicht aus ResNet bzw. ResNeXt.

Aufmerksame Leser haben vielleicht erkannt, dass ein solches Diagramm beliebten „bewährten“ tiefen Netzwerken wie ResNet (Abbildung 5, Mitte), einschließlich ResNeXt Parallel, sehr ähnlich ist Spalten in (Abbildung 5 rechts) und Expertenmix (MoE).

Aus der Perspektive der Entfaltung des Optimierungsschemas liefert dies eine aussagekräftige Erklärung für eine Klasse tiefer neuronaler Netze. Schon vor dem Aufkommen moderner tiefer Netzwerke wurden iterative Optimierungsschemata zur Suche nach Sparsity wie ISTA oder FISTA als lernbare tiefe Netzwerke interpretiert.

Durch Experimente haben sie gezeigt, dass durch Komprimierung eine konstruktive Möglichkeit zur Ableitung tiefer neuronaler Netze, einschließlich ihrer Architektur und Parameter, als vollständig interpretierbare White Box entstehen kann : Seine Schichten werden iterativ und inkrementell im Hinblick auf das grundsätzliche Ziel der Förderung der Einfachheit optimiert. Daher werden für die so erhaltenen tiefen Netzwerke ReduNets, beginnend mit Daten X als Eingabe, die Operatoren und Parameter jeder Schicht vollständig vorwärtsentfaltet konstruiert und initialisiert.

Dies unterscheidet sich stark von der gängigen Praxis beim Deep Learning: Beginnen Sie mit einem zufällig erstellten und initialisierten Netzwerk und nehmen Sie dann globale Anpassungen durch Backpropagation vor. Es ist allgemein anerkannt, dass das Gehirn aufgrund der Notwendigkeit symmetrischer Synapsen und komplexer Formen der Rückkopplung die Rückausbreitung wahrscheinlich nicht als Lernmechanismus nutzen wird. Hier basiert die Forward-Unroll-Optimierung nur auf Vorgängen zwischen benachbarten Schichten, die fest verdrahtet werden können und daher einfacher zu implementieren und auszunutzen sind.

Die „Entwicklung“ künstlicher neuronaler Netze im letzten Jahrzehnt ist leicht zu verstehen und besonders hilfreich bei der Erklärung, wenn wir erkennen, dass die Rolle tiefer Netze selbst darin besteht, eine (gradientenbasierte) iterative Optimierung durchzuführen, um Daten zu komprimieren, zu linearisieren und spärlich zu machen. Warum Nur wenige KI-Systeme zeichnen sich durch einen menschlichen Auswahlprozess aus: von MLP über CNN über ResNet bis Transformer.

Im Gegensatz dazu führen zufällige Suchen nach Netzwerkstrukturen, wie beispielsweise die Suche nach neuronalen Architekturen, nicht zu Netzwerkarchitekturen, die allgemeine Aufgaben effektiv ausführen können. Sie gehen davon aus, dass erfolgreiche Architekturen bei der Simulation iterativer Optimierungsschemata für die Datenkomprimierung immer effektiver und flexibler werden. Dies kann durch die zuvor erwähnten Ähnlichkeiten zwischen ReduNet und ResNet/ResNeXt veranschaulicht werden. Natürlich gibt es noch viele andere Beispiele.

Selbstkonsistenz

Bei der Selbstkonsistenz geht es darum, „wie man lernt“, das heißt, autonome intelligente Systeme suchen nach dem selbstkonsistentesten Modell, um die Außenwelt zu beobachten, indem sie die internen Unterschiede zwischen dem Beobachteten und dem Beobachteten minimieren Wiedergabegerät.

Das Prinzip der Sparsamkeit allein stellt nicht sicher, dass das Lernmodell alle wichtigen Informationen bei der Wahrnehmung der Außenweltdaten erfassen kann.

Beispielsweise kann die Zuordnung jeder Klasse zu einem eindimensionalen „One-Hot“-Vektor durch Minimierung der Kreuzentropie als eine sparsame Form angesehen werden. Es mag einen guten Klassifikator erlernen, aber die erlernten Merkmale fallen in Singletons zusammen, was als „Nervenkollaps“ bekannt ist. Die so erlernten Merkmale enthalten nicht genügend Informationen, um die Originaldaten wiederherzustellen. Selbst wenn wir die allgemeinere Klasse der LDR-Modelle betrachten, bestimmt das Ziel der Geschwindigkeitsreduzierung allein nicht automatisch die korrekten Abmessungen des Umgebungsmerkmalsraums. Wenn die Feature-Space-Dimension zu niedrig ist, passt das erlernte Modell nicht zu den Daten. Wenn sie zu hoch ist, passt das Modell möglicherweise zu gut.

Aus ihrer Sicht besteht das Ziel der Wahrnehmung darin, alle vorhersehbaren Wahrnehmungsinhalte zu lernen. Ein intelligentes System sollte in der Lage sein, eine Verteilung beobachteter Daten aus einer komprimierten Darstellung neu zu generieren, die es, sobald es einmal generiert ist, selbst nicht unterscheiden kann, egal wie sehr es sich bemüht.

Das Papier betont, dass die beiden Prinzipien der Selbstkonsistenz und der Sparsamkeit sich in hohem Maße ergänzen und immer zusammen verwendet werden sollten. Selbstkonsistenz allein gewährleistet keine Komprimierungs- oder Effizienzgewinne.

Passen Sie alle Trainingsdaten mathematisch und rechnerisch mit einem überparametrisierten Modell an oder stellen Sie Konsistenz sicher, indem Sie eine Eins-zu-eins-Zuordnung zwischen Domänen mit denselben Dimensionen erstellen, ohne die Besonderheiten der Datenverteilung zu lernen. Die Struktur ist sehr einfach . Nur durch Komprimierung können intelligente Systeme gezwungen werden, intrinsische niedrigdimensionale Strukturen in hochdimensionalen sensorischen Daten zu entdecken und diese Strukturen im Merkmalsraum auf möglichst kompakte Weise für die zukünftige Verwendung zu transformieren und darzustellen.

Darüber hinaus können wir nur durch Komprimierung die Gründe für eine Überparametrisierung leicht verstehen. Beispielsweise führt DNN normalerweise eine Funktionsverstärkung über Hunderte von Kanälen durch, wenn sein reiner Zweck die Komprimierung in einem hochdimensionalen Merkmalsraum ist. Dann führt dies nicht zu einer Überanpassung: Durch Boosten wird die Nichtlinearität der Daten verringert, wodurch die Komprimierung und Linearisierung erleichtert wird. Die Rolle der nachfolgenden Schichten besteht darin, eine Komprimierung (und Linearisierung) durchzuführen. Je mehr Schichten vorhanden sind, desto besser ist die Komprimierung.

Im Sonderfall der Komprimierung in eine strukturierte Darstellung wie LDR bezeichnet das Papier eine Art automatische Kodierung (Einzelheiten finden Sie im Originalpapier) „Transkription“. Die Schwierigkeit besteht darin, das Ziel rechnerisch erfassbar und damit physikalisch erreichbar zu machen.

Die Ratenreduktion ΔR liefert ein eindeutiges primäres Abstandsmaß zwischen entarteten Verteilungen. Aber es funktioniert nur für Unterräume oder Mischungen von Gaußschen Gleichungen, nicht für allgemeine Verteilungen! Und wir können nur erwarten, dass die Verteilung der internen strukturierten Darstellung z eine Mischung aus Unterräumen oder Gaußschen Verteilungen ist, nicht die ursprünglichen Daten x.

Dies führt zu einer ziemlich tiefgreifenden Frage zum Erlernen „selbstkonsistenter“ Darstellungen: Müssen autonome Systeme wirklich Unterschiede im Datenraum messen, um zu überprüfen, ob ein internes Modell der Außenwelt korrekt ist?

Die Antwort ist nein.

Der Schlüssel besteht darin, zu erkennen, dass der Agent zum Vergleichen von x und x^ nur ihre jeweiligen internen Merkmale z = f(x) und z^ = f(x^) über dieselbe Zuordnung f vergleichen muss, sodass z Kompakt und strukturiert.

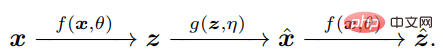
Das Messen von Verteilungsunterschieden im Z-Raum ist tatsächlich genau definiert und effizient: In der natürlichen Intelligenz ist das Erlernen interner Messunterschiede wohl das Einzige, was ein Gehirn mit unabhängigen autonomen Systemen tun kann.

Dadurch entsteht effektiv ein „geschlossenes Feedbacksystem“, wobei der gesamte Prozess in Abbildung 6 dargestellt ist.

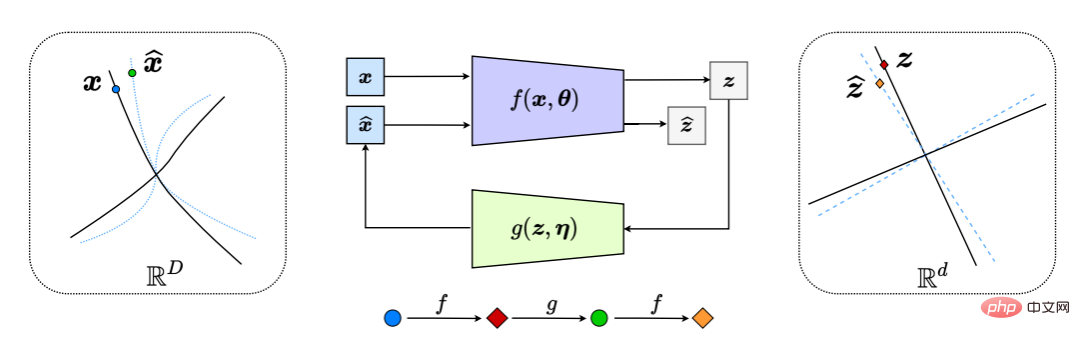
Abbildung 6: Komprimierte Closed-Loop-Transkription nichtlinearer Datenunterverteilungen in LDR (durch internen Vergleich und Minimierung der Differenz zwischen z und z^). Dies führt zu einem natürlichen Jagd-und-Flucht-Spiel zwischen dem Encoder/Sensor f und dem Decoder/Controller g, sodass die Verteilung der dekodierten x^ (blaue gestrichelte Linie) der Verteilung der beobachteten Daten x (schwarz) folgt und mit ihr übereinstimmt durchgezogene Linie).

Man kann die weit verbreitete Praxis, einen DNN-Klassifikator f oder einen Generator g separat zu lernen, als Lernen des offenen Teils eines Systems mit geschlossenem Regelkreis interpretieren (Abbildung 6). Dieser derzeit beliebte Ansatz ist der Steuerung mit offenem Regelkreis sehr ähnlich, von der im Steuerungsbereich seit langem bekannt ist, dass sie problematisch und teuer ist: Das Training eines solchen Teils erfordert die Überwachung der gewünschten Ausgabe (z. B. einer Klassenbezeichnung) des Systems Wenn sich Parameter oder Aufgaben ändern, mangelt es dem Einsatz solcher Open-Loop-Systeme grundsätzlich an Stabilität, Robustheit oder Anpassungsfähigkeit. Beispielsweise kommt es bei Netzwerken zur Tiefenklassifizierung, die in einer überwachten Umgebung trainiert werden, häufig zu katastrophalem Vergessen, wenn sie für die Bewältigung neuer Aufgaben mit neuen Datenkategorien umgeschult werden.

Im Gegensatz dazu sind Systeme mit geschlossenem Regelkreis von Natur aus stabiler und anpassungsfähiger. Tatsächlich haben Hinton et al. dies bereits 1995 vorgeschlagen. Die diskriminierenden und generativen Komponenten müssen als „Wach“- bzw. „Schlaf“-Phasen des gesamten Lernprozesses kombiniert werden.

Allerdings reicht es nicht aus, nur den Kreis zu schließen.

Das Papier plädiert dafür, dass jeder intelligente Agent einen internen Spielmechanismus benötigt, um durch Selbstkritik selbst lernen zu können! Was hier folgt, ist das Konzept des Spielens als universell wirksame Art des Lernens: Wiederholtes Anwenden eines aktuellen Modells oder einer aktuellen Strategie gegen gegnerische Kritik, wodurch das Modell oder die Strategie basierend auf dem Feedback, das durch einen geschlossenen Regelkreis erhalten wird, kontinuierlich verbessert wird!

In einem solchen Rahmen spielt der Encoder f eine doppelte Rolle: Zusätzlich zum Erlernen einer Darstellung z der Daten x durch Maximieren der Ratenreduzierung ΔR(Z) (wie in Abschnitt 2.1 durchgeführt) sollte er auch als dienen Feedback Ein „Sensor“, der aktiv den Unterschied zwischen den Daten x und dem generierten x^ erkennt. Der Decoder g spielt auch eine Doppelrolle: Er ist ein Controller, der mit der Differenz zwischen x und einer bestimmten Genauigkeit verknüpft ist.

Daher kann das optimale „sparsame“ und „selbstkonsistente“ Darstellungstupel (z, f, g) als Gleichgewichtspunkt des Nullsummenspiels zwischen f(θ) und g(η) interpretiert werden, und Nicht basierend auf dem Nutzen einer kombinierten Tarifsenkung:

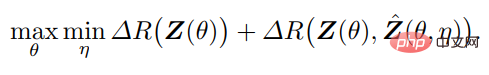
Die obige Diskussion bezieht sich auf die Leistung der beiden Prinzipien in einer überwachten Situation.

Aber das Papier betont, dass das von ihnen vorgeschlagene komprimierte Transkriptionsgerüst mit geschlossenem Regelkreis in der Lage ist, durch Selbstüberwachung und Selbstkritik selbst zu lernen!

Da die Ratenreduktion außerdem eine explizite (Subraum-)Darstellung für die Lernstruktur gefunden hat, erleichtert sie die Beibehaltung von früherem Wissen beim Erlernen neuer Aufgaben/Daten und kann als vorheriges (Gedächtnis) dienen, das die Selbstwahrnehmung aufrechterhält. Konsistenz.

Neueste empirische Studien zeigen, dass dies das erste in sich geschlossene neuronale System mit festem Gedächtnis hervorbringen kann, das inkrementell gute LDR-Darstellungen lernen kann, ohne unter katastrophalem Vergessen zu leiden. Für ein solches geschlossenes System ist das Vergessen (wenn überhaupt) recht elegant.

Darüber hinaus kann die erlernte Darstellung weiter gefestigt werden, wenn Bilder aus alten Kategorien dem System erneut zur Überprüfung zugeführt werden – eine Funktion, die der des menschlichen Gedächtnisses sehr ähnlich ist. In gewisser Weise stellt diese eingeschränkte Formulierung mit geschlossenem Regelkreis im Wesentlichen sicher, dass die Bildung des visuellen Gedächtnisses bayesianisch und adaptiv sein kann – vorausgesetzt, diese Eigenschaften sind ideal für das Gehirn.

Wie in Abbildung 8 dargestellt, weist die so erlernte automatische Codierung nicht nur eine gute Probenkonsistenz auf, sondern die erlernten Merkmale weisen auch eine klare und aussagekräftige lokale niedrigdimensionale (dünne) Struktur auf.

Abbildung 8: Links: Vergleich zwischen dem automatisch kodierten x, das in der unbeaufsichtigten Einstellung des CIFAR-10-Datensatzes (50.000 Bilder mit 10 Klassen) gelernt wurde, und dem entsprechenden dekodierten x^. Rechts: t-SNE unbeaufsichtigt erlernter Features für 10 Klassen und Visualisierung mehrerer Stadtteile und der zugehörigen Bilder. Beachten Sie die lokal dünne (nahezu eindimensionale) Struktur in den visualisierten Features, projiziert aus einem Feature-Raum mit Hunderten von Dimensionen.

Noch überraschender ist, dass in den für die Klasse erlernten Features unterraum- oder merkmalsbezogene Blockdiagonalstrukturen auftauchen, selbst wenn während des Trainings keine Klasseninformationen bereitgestellt werden (Abbildung 9)! Daher ähnelt die Struktur der erlernten Merkmale den kategorieselektiven Regionen, die im Gehirn von Primaten beobachtet werden.

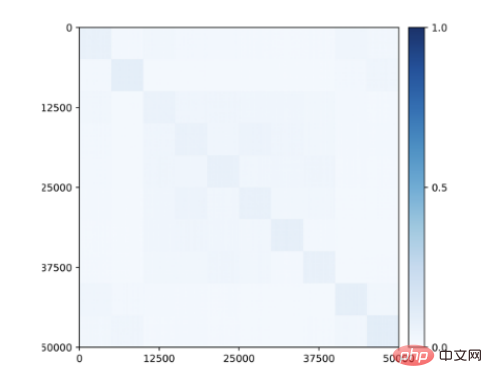
Abbildung 9: Korrelation zwischen unbeaufsichtigt erlernten Merkmalen für 50.000 Bilder, die zu 10 Kategorien (CIFAR-10) gehören, mittels Closed-Loop-Transkription. Es entstehen klassenkonsistente Blockdiagonalstrukturen ohne jegliche Aufsicht.

Universelle Lernmaschine: Kombination von 3D-Vision und Grafik

Zusammenfassung, Sparsamkeit und Selbstkonsistenz offenbaren die Rolle tiefer Netzwerke als Modelle der nichtlinearen Zuordnung zwischen externen Beobachtungen und internen Darstellungen.

Darüber hinaus wird in der Arbeit betont, dass Kompressionsstrukturen mit geschlossenem Regelkreis in der Natur allgegenwärtig sind und auf alle intelligenten Lebewesen anwendbar sind. Dies kann im Gehirn (Komprimierung sensorischer Informationen), in den Schaltkreisen des Rückenmarks (Komprimierung von Muskelbewegungen) beobachtet werden. und DNA (Komprimierung der Funktion von Proteinen) Informationen) und so weiter biologische Beispiele. Daher glauben sie, dass die komprimierte Transkription im geschlossenen Regelkreis der universelle Lernmotor hinter allem intelligenten Verhalten sein könnte. Es ermöglicht intelligenten Organismen und Systemen, niedrigdimensionale Strukturen aus scheinbar komplexen und unorganisierten Eingaben zu entdecken und zu verfeinern und sie in kompakte und organisierte interne Strukturen umzuwandeln, die man sich merken und nutzen kann.

Um die Allgemeingültigkeit dieses Rahmenwerks zu veranschaulichen, untersucht der Artikel zwei weitere Aufgaben: 3D-Wahrnehmung und Entscheidungsfindung (LeCun betrachtet diese beiden Schlüsselmodule autonomer intelligenter Systeme). Dieser Artikel ist organisiert und stellt nur den geschlossenen Kreislauf von Computer Vision und Computergrafik in der 3D-Wahrnehmung vor.

Das klassische Paradigma der 3D-Vision, das David Marr in seinem einflussreichen Buch Vision vorgeschlagen hat, befürwortet einen „Teile-und-herrsche“-Ansatz, der die 3D-Wahrnehmungsaufgabe in mehrere modulare Prozesse unterteilt: von der 2D-Verarbeitung auf niedriger Ebene (z. B. Kantenerkennung, Kontur). Skizzieren), mittleres 2,5D-Parsing (z. B. Gruppierung, Segmentierung, Form und Boden) und erweiterte 3D-Rekonstruktion (z. B. Pose, Form) und Erkennung (z. B. Objekt), während im Gegensatz dazu die komprimierte geschlossene Schleife Transkriptionsrahmen befürwortet „gemeinsame Konstruktion“ Gedanken.

Wahrnehmung ist komprimierte Closed-Loop-Transkription? Genauer gesagt sollten 3D-Darstellungen der Form, des Aussehens und sogar der Dynamik von Objekten in der Welt die kompaktesten und strukturiertesten Darstellungen sein, die unser Gehirn intern entwickelt, um alle wahrgenommenen visuellen Beobachtungen entsprechend zu interpretieren. Wenn ja, dann legen diese beiden Prinzipien nahe, dass eine kompakte und strukturierte 3D-Darstellung das zu suchende interne Modell ist. Das bedeutet, dass wir Computer Vision und Computergrafik in einem Closed-Loop-Computing-Framework vereinen können und sollten, wie in der folgenden Abbildung dargestellt:

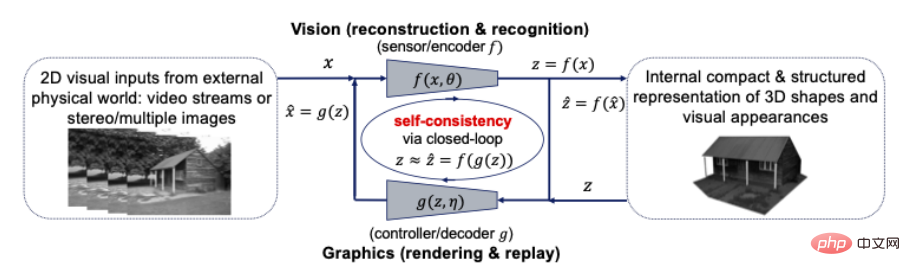
Abbildung 10: Closed-Loop-Beziehung zwischen Computer Vision und Grafik für eine kompakte Summe visueller Elemente Eingaben Strukturierte 3D-Modelle

Computer Vision wird oft als der Vorwärtsprozess der Rekonstruktion und Identifizierung interner 3D-Modelle für alle visuellen 2D-Eingaben erklärt, während Computergrafik den umgekehrten Prozess der Darstellung und Animation interner 3D-Modelle darstellt. Die direkte Kombination dieser beiden Prozesse in einem geschlossenen Kreislaufsystem könnte enorme rechnerische und praktische Vorteile bringen: Alle reichhaltigen Strukturen in Geometrie, visuellem Erscheinungsbild und Dynamik (wie Sparsität und Glätte) können größtenteils zusammen in einem einheitlichen 3D-Modell verwendet werden kompakt und konsistent mit allen visuellen Eingaben.

Erkennungstechniken in der Computer Vision können Computergrafiken dabei helfen, kompakte Modelle im Form- und Erscheinungsraum zu erstellen und neue Möglichkeiten zur Erstellung realistischer 3D-Inhalte bereitzustellen. Andererseits können 3D-Modellierungs- und Simulationstechniken in der Computergrafik die Eigenschaften und das Verhalten realer Objekte und Szenen, die von Computer-Vision-Algorithmen analysiert werden, vorhersagen, lernen und überprüfen. Die visuelle und grafische Community praktiziert seit langem einen Ansatz der „synthetischen Analyse“.

Einheitliche Darstellung von Aussehen und Form? Bildbasiertes Rendering, bei dem neue Ansichten durch Lernen aus einem bestimmten Satz von Bildern generiert werden, kann als früher Versuch angesehen werden, die Lücke zwischen Vision und Grafik mit sparsamen und in sich konsistenten Prinzipien zu schließen. Insbesondere das plenoptische Sampling zeigt, dass geglättete Bilder (Selbstkonsistenz) mit der minimal erforderlichen Anzahl von Bildern (Sparsamkeit) erreicht werden können.

Broader Intelligence​

Die Neurowissenschaften der Intelligenz

Man würde erwarten, dass grundlegende Intelligenzprinzipien einen erheblichen Einfluss auf die Gestaltung des Gehirns haben. Die Prinzipien der Sparsamkeit und Selbstkonsistenz werfen neues Licht auf mehrere experimentelle Beobachtungen des visuellen Systems von Primaten. Noch wichtiger ist, dass sie zeigen, worauf bei zukünftigen Experimenten zu achten ist.

Das Autorenteam hat gezeigt, dass die bloße Suche nach internen, sparsamen und prädiktiven Darstellungen ausreicht, um eine „Selbstüberwachung“ zu erreichen, die es Strukturen ermöglicht, automatisch in der endgültigen Darstellung zu erscheinen, die durch komprimierte Transkription mit geschlossenem Regelkreis gelernt wurde.

Abbildung 9 zeigt beispielsweise, dass unbeaufsichtigtes Datentranskriptionslernen automatisch Merkmale verschiedener Kategorien unterscheidet und so eine Erklärung für die im Gehirn beobachteten kategorieselektiven Darstellungen liefert. Diese Merkmale liefern auch eine vernünftige Erklärung für die weit verbreiteten Beobachtungen von Sparse-Codierung und Subraum-Codierung im Gehirn von Primaten. Darüber hinaus deuten neuere neurowissenschaftliche Untersuchungen neben der visuellen Datenmodellierung darauf hin, dass auch andere strukturierte Darstellungen, die im Gehirn entstehen (z. B. „Ortszellen“), das Ergebnis der Kodierung räumlicher Informationen in höchst komprimierter Weise sein können.

Man kann sagen, dass das MCR2-Prinzip (Maximum Coding Rate Reduction) im Geiste dem „Prinzip der Minimierung der freien Energie“ in der Kognitionswissenschaft ähnelt, das versucht, die Bayes'sche Energie durch Reasoning zu minimieren und den Rahmen dafür vorgibt. Aber im Gegensatz zum allgemeinen Konzept der freien Energie ist die Ratenreduzierung rechnerisch nachvollziehbar und direkt optimierbar, da sie in einer geschlossenen Form ausgedrückt werden kann. Darüber hinaus legt das Zusammenspiel dieser beiden Prinzipien nahe, dass das autonome Lernen des richtigen Modells (der richtigen Klasse) durch ein Maximierungsspiel mit geschlossenem Regelkreis dieses Nutzens und nicht nur durch Minimierung erreicht werden sollte. Daher glauben sie, dass das komprimierte Transkriptions-Framework mit geschlossenem Regelkreis eine neue Perspektive dafür bietet, wie Bayes'sche Inferenz praktisch umgesetzt werden kann.

Dieser Rahmen ist ihrer Ansicht nach auch eine Veranschaulichung der vom Gehirn verwendeten Gesamtlernarchitektur, die Feed-Forward-Segmente durch Entfaltung von Optimierungsschemata erstellen kann, ohne dass durch Backpropagation von zufälligen Netzwerken gelernt werden muss. Darüber hinaus gibt es einen ergänzenden generativen Teil des Frameworks, der ein geschlossenes Feedbacksystem zur Steuerung des Lernens bilden kann.

Schließlich enthüllt das Framework das schwer fassbare „Vorhersagefehler“-Signal, nach dem viele Neurowissenschaftler suchen, die sich für die Gehirnmechanismen der „prädiktiven Codierung“ interessieren, einem Rechenschema, das mit der komprimierten Transkription im geschlossenen Regelkreis in Resonanz steht: um Berechnungen durchzuführen Um es einfacher zu machen, sollte der Unterschied zwischen den eingehenden und generierten Beobachtungen in der letzten Phase der Darstellung gemessen werden.

Auf dem Weg zu höheren Intelligenzniveaus

Die Arbeit von Ma Yi et al. geht davon aus, dass die komprimierte Closed-Loop-Transkription rechnerisch besser nachvollziehbar und skalierbar ist als das von Hinton et al. Darüber hinaus stellt das wiederkehrende Lernen nichtlinearer Kodierungs-/Dekodierungsabbildungen (häufig manifestiert als tiefe Netzwerke) im Wesentlichen eine wichtige Brücke zwischen externen unorganisierten rohen sensorischen Daten (wie Sehen, Hören usw.) und internen kompakten und strukturierten „Schnittstellen“ dar.

Sie wiesen jedoch auch darauf hin, dass diese beiden Prinzipien nicht unbedingt alle Aspekte der Intelligenz erklären. Die Rechenmechanismen, die der Entstehung und Entwicklung von semantischem, symbolischem oder logischem Denken auf hoher Ebene zugrunde liegen, sind nach wie vor unklar. Bis heute wird darüber diskutiert, ob diese fortgeschrittene symbolische Intelligenz durch kontinuierliches Lernen entstehen kann oder hart codiert werden muss.

Nach Ansicht der drei Wissenschaftler sind strukturierte interne Repräsentationen wie Unterräume – die jeweils einer diskreten (Objekt-)Kategorie entsprechen – ein notwendiger Zwischenschritt für die Entstehung hochrangiger semantischer oder symbolischer Konzepte. Andere statistische, kausale oder logische Beziehungen zwischen solchen abstrakten diskreten Konzepten können weiter vereinfacht und als kompakte und strukturierte (z. B. spärliche) Graphen modelliert werden, wobei jeder Knoten einen Unterraum/eine Unterkategorie darstellt. Diagramme können durch automatische Kodierung erlernt werden, um Selbstkonsistenz sicherzustellen.

Sie spekulieren, dass die Entstehung und Entwicklung fortgeschrittener Intelligenz (mit teilbarem symbolischem Wissen) nur auf der Grundlage kompakter und strukturierter Darstellungen möglich ist, die von einzelnen Agenten gelernt werden. Daher schlugen sie vor, dass neue Prinzipien für die Entstehung fortgeschrittener Intelligenz (sofern fortgeschrittene Intelligenz vorhanden ist) durch effektiven Informationsaustausch oder Wissenstransfer zwischen intelligenten Systemen erforscht werden sollten.

Darüber hinaus sollten höhere Intelligenzniveaus zwei Dinge mit den beiden Prinzipien, die wir in diesem Artikel vorschlagen, gemeinsam haben:

• Interpretierbarkeit: Alle Prinzipien sollten dazu beitragen, die Rechenmechanismen der Intelligenz als White Box aufzudecken, einschließlich messbarer Ziele. zugehörige Computerarchitektur und Struktur zum Lernen von Darstellungen.
• Berechenbarkeit: Jedes neue Intelligenzprinzip muss rechnerisch nachvollziehbar und skalierbar, durch Computer oder Naturphysik erreichbar und letztendlich durch wissenschaftliche Beweise bestätigt sein.

Nur mit Interpretierbarkeit und Berechenbarkeit können wir den Fortschritt der künstlichen Intelligenz vorantreiben, ohne uns auf die aktuellen teuren und zeitaufwändigen „Trial-and-Error“-Methoden zu verlassen, und in der Lage sein, die dafür erforderlichen Mindestdaten und Rechenressourcen zu beschreiben Aufgaben, anstatt einfach nur den Brute-Force-Ansatz „Größer ist besser“ zu befürworten. Weisheit sollte nicht das Vorrecht der einfallsreichsten Menschen sein. Mit den richtigen Prinzipien sollte jeder in der Lage sein, die nächste Generation intelligenter Systeme zu entwerfen und zu bauen, ob groß oder klein, deren Autonomie, Fähigkeiten und Effizienz letztendlich nachahmen oder sogar übertreffen die von Tieren und Menschen.

Link zum Papier:

​https://arxiv.org/pdf/2207.04630.pdf​

Das obige ist der detaillierte Inhalt vonVerfolgen Sie nicht blind große Modelle und häufen Sie Rechenleistung an! Shen Xiangyang, Cao Ying und Ma Yi schlugen zwei Grundprinzipien für das Verständnis von KI vor: Sparsamkeit und Selbstkonsistenz. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!