Heim >Technologie-Peripheriegeräte >KI >Integration von Zeitreihenmodellen zur Verbesserung der Prognosegenauigkeit
Integration von Zeitreihenmodellen zur Verbesserung der Prognosegenauigkeit
- PHPznach vorne
- 2023-05-11 09:10:051083Durchsuche
Verwenden Sie Catboost, um Signale aus RNN-, ARIMA- und Prophet-Modellen für die Vorhersage zu extrahieren.
Die Integration verschiedener schwacher Lernender kann die Vorhersagegenauigkeit verbessern, aber wenn unser Modell bereits sehr leistungsfähig ist, kann Ensemble-Lernen oft auch ein Tüpfelchen auf dem i sein. Die beliebte Bibliothek für maschinelles Lernen scikit-learn bietet einen StackingRegressor, der für Zeitreihenaufgaben verwendet werden kann. Aber StackingRegressor hat eine Einschränkung; es akzeptiert nur andere Scikit-Learn-Modellklassen und APIs. Daher können Modelle wie ARIMA, die in scikit-learn nicht verfügbar sind, oder Modelle aus tiefen neuronalen Netzen nicht verwendet werden. In diesem Beitrag werde ich zeigen, wie man die Vorhersagen des Modells stapelt, die wir sehen können.

Wir werden die folgenden Pakete verwenden:
pip install --upgrade scalecast conda install tensorflow conda install shap conda install -c conda-forge cmdstanpy pip install prophet# 🎜 🎜#DatensatzDer Datensatz wird stündlich generiert und ist in einen Trainingssatz (700 Beobachtungen) und einen Testsatz (48 Beobachtungen) unterteilt. Der folgende Code liest die Daten und speichert sie im Forecaster-Objekt:
import pandas as pd import numpy as np from scalecast.Forecaster import Forecaster from scalecast.util import metrics import matplotlib.pyplot as plt import seaborn as sns def read_data(idx = 'H1', cis = True, metrics = ['smape']): info = pd.read_csv( 'M4-info.csv', index_col=0, parse_dates=['StartingDate'], dayfirst=True, ) train = pd.read_csv( f'Hourly-train.csv', index_col=0, ).loc[idx] test = pd.read_csv( f'Hourly-test.csv', index_col=0, ).loc[idx] y = train.values sd = info.loc[idx,'StartingDate'] fcst_horizon = info.loc[idx,'Horizon'] cd = pd.date_range( start = sd, freq = 'H', periods = len(y), ) f = Forecaster( y = y, # observed values current_dates = cd, # current dates future_dates = fcst_horizon, # forecast length test_length = fcst_horizon, # test-set length cis = cis, # whether to evaluate intervals for each model metrics = metrics, # what metrics to evaluate ) return f, test.values f, test_set = read_data() f # display the Forecaster objectDas Ergebnis sieht so aus:
# 🎜🎜#
Bevor wir mit der Erstellung des Modells beginnen, müssen wir daraus die einfachste Vorhersage generieren. Die naive Methode besteht darin, die letzten 24 zu propagieren Beobachtungen Wert.
f.set_estimator('naive')
f.manual_forecast(seasonal=True)
Dann verwenden Sie ARIMA, LSTM und Prophet als Benchmarks.
ARIMA
Autoregressive Integrated Moving Average ist eine beliebte und einfache Zeitreihentechnik, die die Verzögerung und den Fehler einer Reihe nutzt, um ihre Zukunft auf lineare Weise vorherzusagen. Durch EDA haben wir festgestellt, dass diese Serie stark saisonabhängig ist. Also habe ich mich schließlich für das saisonale ARIMA-Modell mit der Reihenfolge (5,1,4) x(1,1,1,24) entschieden.
f.set_estimator('arima')
f.manual_forecast(
order = (5,1,4),
seasonal_order = (1,1,1,24),
call_me = 'manual_arima',
)
LSTM
Wenn ARIMA ein relativ einfaches Zeitreihenmodell ist, dann ist LSTM eine der fortgeschritteneren Methoden. Es handelt sich um eine Deep-Learning-Technik mit vielen Parametern, einschließlich eines Mechanismus zur Entdeckung langfristiger und kurzfristiger Muster in sequentiellen Daten, was sie theoretisch ideal für Zeitreihen macht. Hier verwenden wir Tensorflow, um dieses Modell zu erstellen Die Schlussfolgerung von Trends ist manchmal unrealistisch und lokale Muster werden durch autoregressive Modellierung nicht berücksichtigt. Aber es hat auch seine eigenen Eigenschaften. 1. Es wendet automatisch Feiertagseffekte auf das Modell an und berücksichtigt auch verschiedene Arten von Saisonalität. Dies alles kann mit dem vom Benutzer geforderten Minimum durchgeführt werden, daher verwende ich es lieber als Signal und nicht als endgültige Vorhersage.
f.set_estimator('rnn')
f.manual_forecast(
lags = 48,
layers_struct=[
('LSTM',{'units':100,'activation':'tanh'}),
('LSTM',{'units':100,'activation':'tanh'}),
('LSTM',{'units':100,'activation':'tanh'}),
],
optimizer = 'Adam',
epochs = 15,
plot_loss = True,
validation_split=0.2,
call_me = 'rnn_tanh_activation',
)
f.manual_forecast(
lags = 48,
layers_struct=[
('LSTM',{'units':100,'activation':'relu'}),
('LSTM',{'units':100,'activation':'relu'}),
('LSTM',{'units':100,'activation':'relu'}),
],
optimizer = 'Adam',
epochs = 15,
plot_loss = True,
validation_split=0.2,
call_me = 'rnn_relu_activation',
)
Vergleichsergebnisse
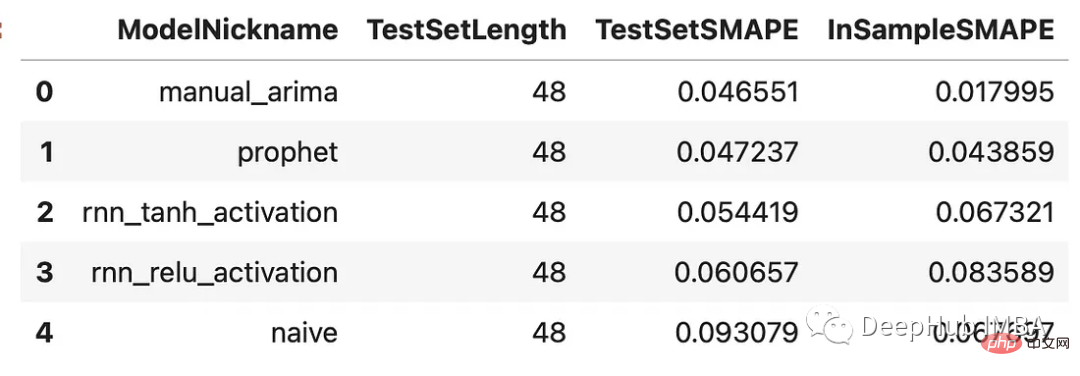
Da wir nun Vorhersagen für jedes Modell generiert haben, sehen wir uns an, wie sie im Validierungssatz, dem Validierungssatz, abschneiden sind die letzten 48 Beobachtungen in unserem Trainingssatz. Jedes Modell übertrifft die naive Methode. Das ARIMA-Modell schnitt mit einem prozentualen Fehler von 4,7 % am besten ab, gefolgt vom Prophet-Modell. Sehen wir uns an, wie sich alle Vorhersagen auf den Validierungssatz beziehen: Alle diese Modelle schneiden in dieser Zeitreihe einigermaßen gut ab, ohne große Abweichungen zwischen ihnen. Stapeln wir sie!
Gestapeltes Modell
Jedes gestapelte Modell erfordert einen endgültigen Schätzer, der die verschiedenen Schätzungen aus den anderen Modellen filtert und so eine neue Prognose erstellt. Wir werden die vorherigen Ergebnisse mit dem Catboost-Schätzer überlagern. Catboost ist ein leistungsstarkes Programm und man hofft, dass es das beste Signal jedes angewendeten Modells bereichert.
f.set_estimator('prophet')
f.manual_forecast()
Der obige Code fügt die Vorhersagen von jedem bewerteten Modell zu einem Forecaster-Objekt hinzu. Diese Vorhersagen werden als „Signale“ bezeichnet. Sie werden genauso behandelt wie alle anderen im selben Objekt gespeicherten Kovariaten. Die letzten 48 Lag-Serien werden hier auch als zusätzliche Regressoren hinzugefügt, die das Catboost-Modell für Vorhersagen verwenden kann. Nennen wir nun drei Catboost-Modelle: eines, das alle verfügbaren Signale und Verzögerungen verwendet, eines, das nur Signale verwendet, und eines, das nur Verzögerungen verwendet.
results = f.export(determine_best_by='TestSetSMAPE') ms = results['model_summaries'] ms[ [ 'ModelNickname', 'TestSetLength', 'TestSetSMAPE', 'InSampleSMAPE', ] ]
Die Ergebnisse aller Modelle können unten verglichen werden. Wir werden uns zwei Metriken ansehen: SMAPE und den mittleren absoluten skalierten Fehler (MASE). Dies sind zwei Kennzahlen, die im tatsächlichen M4-Wettbewerb verwendet werden.
f.plot(order_by="TestSetSMAPE",ci=True) plt.show()
可以看到,通过组合来自不同类型模型的信号生成了两个优于其他估计器的估计器:使用所有信号训练的Catboost模型和只使用信号的Catboost模型。这两种方法的样本误差都在2.8%左右。下面是对比图:
fig, ax = plt.subplots(figsize=(12,6)) f.plot( models = ['catboost_all_reg','catboost_signals_only'], ci=True, ax = ax ) sns.lineplot( x = f.future_dates, y = test_set, ax = ax, label = 'held out actuals', color = 'darkblue', alpha = .75, ) plt.show()

哪些信号最重要?
为了完善分析,我们可以使用shapley评分来确定哪些信号是最重要的。Shapley评分被认为是确定给定机器学习模型中输入的预测能力的最先进的方法之一。得分越高,意味着输入在特定模型中越重要。
f.export_feature_importance('catboost_all_reg')

上面的图只显示了前几个最重要的预测因子,但我们可以从中看出,ARIMA信号是最重要的,其次是序列的第一个滞后,然后是Prophet。RNN模型的得分也高于许多滞后模型。如果我们想在未来训练一个更轻量的模型,这可能是一个很好的起点。
总结
在这篇文章中,我展示了在时间序列上下文中集成模型的力量,以及如何使用不同的模型在时间序列上获得更高的精度。这里我们使用scalecast包,这个包的功能还是很强大的,如果你喜欢,可以去它的主页看看:https://github.com/mikekeith52/scalecast
本文的数据集是M4的时序竞赛:https://github.com/Mcompetitions/M4-methods
使用代码在这里:https://scalecast-examples.readthedocs.io/en/latest/misc/stacking/custom_stacking.html
Das obige ist der detaillierte Inhalt vonIntegration von Zeitreihenmodellen zur Verbesserung der Prognosegenauigkeit. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Technologietrends, die Sie im Jahr 2023 im Auge behalten sollten
- Wie künstliche Intelligenz Rechenzentrumsteams neue Alltagsaufgaben beschert
- Können künstliche Intelligenz oder Automatisierung das Problem der geringen Energieeffizienz in Gebäuden lösen?
- OpenAI-Mitbegründer im Interview mit Huang Renxun: Die Argumentationsfähigkeiten von GPT-4 haben noch nicht die Erwartungen erfüllt
- Dank der OpenAI-Technologie übertrifft Bing von Microsoft Google im Suchverkehr

