Wie zeichne ich eine konvexe Hülle in Python?

ConvexHull

ConvexHull ist eine räumliche Klasse. Ihre Hauptfunktion besteht darin, die Kanten einer Menge von Punkten zu finden und eine konvexe Hülle zu erstellen. Der notwendige Initialisierungsparameter ist eine Punktmenge, das Punktmengenformat ist ein Array von n×m Dimensionen, n ist die Anzahl der Punkte in der Punktmenge und m ist die Dimension des Punktes.

from scipy.spatial import ConvexHull
import matplotlib.pyplot as plt
import numpy as np

pts = np.random.rand(30, 2)
hull = ConvexHull(pts)
plt.plot(pts[:,0], pts[:,1], 'o')
for i in hull.simplices:
    plt.plot(pts[i, 0], pts[i, 1], 'k-')

plt.show()

wobei simplex die Seriennummer des Indexpunkts ist. Der Effekt nach dem Zeichnen ist wie folgt: „Inkremental“ ist ein boolescher Parameter .

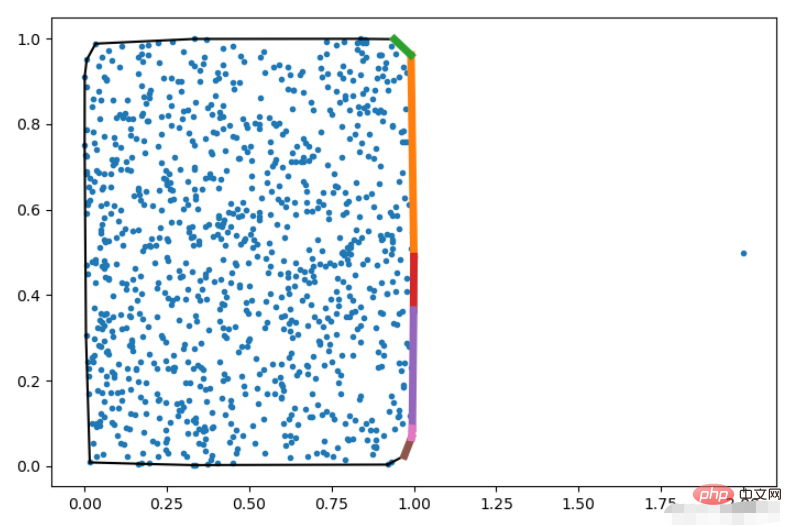
Die spezifischen Parameter von qhull_options können in qhull angezeigt werden. Nachfolgend wird nur QG demonstriert.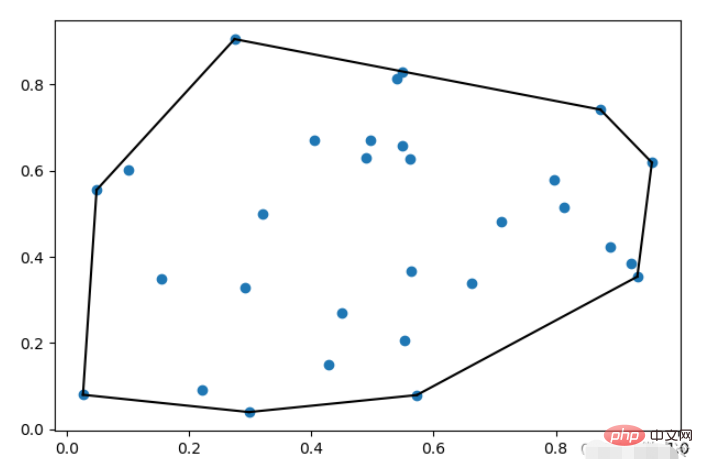

QG

QGn bedeutet, dass der n-te Punkt als Beobachtungspunkt betrachtet wird. Wenn die Eckpunkte nach der Division durch die konvexe Hülle verbunden und als Wand verwendet werden, sind dies die Punkte, die vom Beobachtungspunkt gesehen werden können Als gut markiert, ist der Effekt wie unten gezeigt.

pts = np.random.rand(1000, 2)
# 添加一个观察点
pts = np.vstack([pts, np.array([[2,0.5]])])
hull = ConvexHull(pts, qhull_options='QG1000')
plt.plot(pts[:,0], pts[:,1], '.')
for i in hull.simplices:
    plt.plot(pts[i, 0], pts[i, 1], 'k-')

for i in hull.simplices[hull.good]:
    plt.plot(pts[i, 0],pts[i, 1], lw=5)

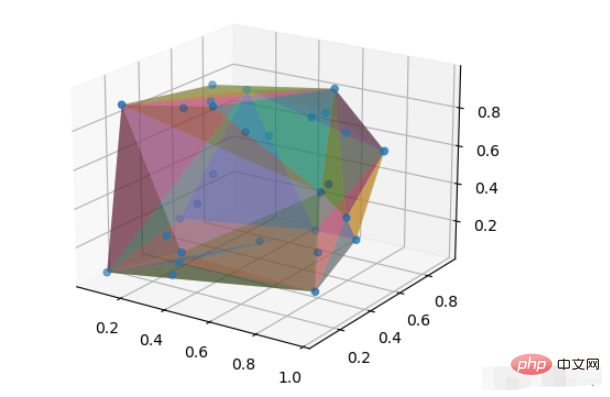
plt.show()

und die konvexe Hülle im dreidimensionalen Fall sollte natürlich eine dreidimensionale Geometrie sein. Auf jede beliebige Dimension erweitert, ist die konvexe Hülle tatsächlich ein Simplex. Die Simplices in ConvexHull sind die Punkte, die den Simplex bilden und im Ursprungssatz indiziert sind. Das Beispiel sieht wie folgt aus

pts = np.random.rand(30, 3)
hull = ConvexHull(pts)
ax = plt.subplot(projection='3d')
ax.scatter(pts[:,0], pts[:,1], pts[:,2])
for i in hull.simplices:
    ax.plot_trisurf(pts[i, 0], pts[i, 1], pts[i,2], alpha=0.5)

plt.show()

Der Alpha-Parameter wird verwendet, um die Transparenz der dreieckigen Oberfläche anzupassen, sodass die Punkte innerhalb der konvexen Hülle durch die konvexe Hülle sichtbar sind.

Der Effekt ist wie folgt

ConvexHull-Attribut

Das Konzept eines Simplex wurde bereits eingeführt, das heißt, die aus der konvexen Hülle bestehende Figur ist ein Simplex. Im zweidimensionalen Fall ist die konvexe Hülle von Liniensegmenten umgeben. Im dreidimensionalen Fall ist die konvexe Hülle von Ebenen umgeben durch Hyperflächen. Da der Begriff der Hyperfläche keine Grenzen kennt, wird die konvexe Hüllenfläche mit Eckpunkten und Kanten im Folgenden als Simplex-Hyperfläche bezeichnet.

Häufig verwendete Attribute in der ConvexHull-Klasse sind wie folgt

Punktsatz, umgeben von einer konvexen Hülle

Vertices-Index des Simplex-Scheitelpunkts im Punktsatz

Simplices Simplex-Hyperflächen-Scheitelpunkt

• Nachbarn super Oberfläche Indizes benachbarter Hyperflächen

• Gleichungen Parameter von Hyperflächengleichungen

• Beispiele für Hyperflächengleichungen im dreidimensionalen Fall sind wie folgt, das heißt, jede Hyperfläche hat 4 Parameter

  >>> hull.equations
  array([[-0.5509472 ,  0.72386104, -0.41530999, -0.36369123],
         [-0.26155355,  0.16210178, -0.95147925,  0.02022163],
         [-0.99132368, -0.0460725 ,  0.12310441,  0.045523  ],
         [-0.98526526, -0.07170442,  0.15527666,  0.04749854],
         [-0.15900968, -0.98529789, -0.06248198,  0.13294496],
     # .......

Das obige ist der detaillierte Inhalt vonWie zeichne ich eine konvexe Hülle in Python?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!