Anwendung kausaler Schlussfolgerungen in Micro-View-Anreizen und Angebots- und Nachfrageszenarien

1. Kausaler Schlussfolgerungs- und Anreizalgorithmus

1 Modell

Lassen Sie uns zunächst kurz den Hintergrund des Red-Envelope-Incentive-Geschäfts von Tencent Weishi vorstellen. Ähnlich wie bei anderen Produkten und Szenarien geben wir innerhalb eines bestimmten Budgets einige Bargeldanreize an Benutzer von Tencent Weishi aus, in der Hoffnung, durch Bargeldanreize die Bindung der Benutzer am nächsten Tag und die Nutzungszeit am selben Tag zu maximieren. Die wichtigste Form von Bargeldanreizen besteht darin, in unregelmäßigen Abständen rote Bargeldumschläge in einer unbestimmten Anzahl und einem unbestimmten Betrag an Benutzer auszugeben. Die drei oben genannten „Unsicherheiten“ werden letztlich durch Algorithmen bestimmt. Diese drei „Unsicherheiten“ werden auch als die drei Elemente der Red-Envelope-Anreizstrategie bezeichnet.

Lassen Sie uns als Nächstes über die abstrakten Formen verschiedener Cash-Incentive-Strategien sprechen. Die erste drückt die Strategie in Form einer roten Hüllkurvensequenz aus, z. B. durch Nummerierung der roten Hüllkurvensequenz und anschließende unabhängige Nummerierung jeder Behandlung in Form von One-Hot. Sein Vorteil besteht darin, dass mehr Details dargestellt werden können, beispielsweise der Abstand zwischen den einzelnen roten Umschlägen und andere detaillierte Strategien sowie die entsprechenden Auswirkungen. Dies erfordert jedoch zwangsläufig mehr Variablen zur Darstellung der Strategie. Darüber hinaus sind bei der Erkundung und Auswahl der Strategie mehr Berechnungen erforderlich. Die zweite Form, die einen Drei-Elemente-Vektor zur Darstellung der Strategie verwendet, ist flexibler und effizienter bei der Erkundung, lässt jedoch einige Details außer Acht. Der dritte Weg ist mathematischer, das heißt, die rote Hüllkurvensequenz wird direkt zu einer Funktion über die Zeit t, und die Parameter in der Funktion können einen Vektor bilden, um die Strategie darzustellen. Die Modellierung kausaler Probleme und die Darstellung von Strategien bestimmen maßgeblich die Genauigkeit und Effizienz der Kausalwirkungsschätzung.

Unter der Annahme, dass wir eine gute Strategieabstraktion und Vektordarstellung haben, müssen wir als Nächstes ein Algorithmus-Framework auswählen. Hier gibt es drei Frameworks. Das erste Framework ist in der Branche relativ ausgereift und verwendet kausale Schlussfolgerungen in Kombination mit der Optimierung von Einschränkungen mit mehreren Zielen, um Strategien zuzuweisen und zu optimieren. In diesem Rahmen ist die kausale Schlussfolgerung hauptsächlich für die Schätzung der zentralen Benutzerindikatoren verantwortlich, die verschiedenen Strategien entsprechen. Dies nennen wir Benutzerbindung und Verbesserung der Dauer. Nach der Schätzung verwenden wir eine Multi-Objective-Constraint-Optimierung, um eine Offline-Budgetstrategiezuweisung durchzuführen, um die Budgetbeschränkungen zu erfüllen. Die zweite ist das Offline-Lernen zur Verstärkung in Kombination mit der Methode zur Optimierung von Einschränkungen mit mehreren Zielen. Ich persönlich halte diese Methode aus zwei Hauptgründen für erfolgversprechender. Der erste Grund ist, dass es in tatsächlichen Anwendungsszenarien viele Strategien gibt und das verstärkende Lernen selbst den Strategieraum effizient erkunden kann. Da unsere Strategien gleichzeitig abhängig sind, kann das verstärkende Lernen die Abhängigkeit zwischen Strategien modellieren dass das Wesen der starken Offline-Chemie tatsächlich ein Problem der kontrafaktischen Schätzung ist, das selbst starke kausale Eigenschaften hat. Leider haben wir in unserem Szenario Offline-Verstärkungslernen ausprobiert, dessen Online-Effekt jedoch nicht die gewünschten Ergebnisse erzielte. Der Grund liegt einerseits in unserem Methodenproblem, andererseits ist es hauptsächlich durch die Daten begrenzt. Um ein gutes Offline-Lernmodell zur Verstärkung zu trainieren, muss die Strategieverteilung in den Daten breit genug oder gleichmäßig genug sein. Mit anderen Worten: Unabhängig davon, ob wir Zufallsdaten oder Beobachtungsdaten verwenden, hoffen wir, so viele solcher Strategien wie möglich zu untersuchen und die Verteilung relativ gleichmäßig zu gestalten, sodass wir die Anzahl der geschätzten Varianzen reduzieren können. Das letzte Algorithmus-Framework ist in Werbeszenarien relativ ausgereift. Wir verwenden Online-Verstärkungslernen, um Verkehr und Budget zu kontrollieren. Der Vorteil dieser Methode besteht darin, dass sie zeitnah und schnell auf Online-Notfälle reagieren und gleichzeitig das Budget genauer kontrollieren kann. Nach der Einführung von Ursache und Wirkung ist der Indikator, den wir für die Verkehrsauswahl oder -steuerung verwenden, nicht mehr der ECPM-Indikator. Dies kann eine Verbesserung der Aufbewahrung und Dauer sein, die wir jetzt schätzen. Nach einer Reihe praktischer Versuche haben wir uns schließlich für das erste Algorithmus-Framework entschieden, bei dem es sich um kausale Inferenz in Kombination mit der Optimierung von Mehrziel-Beschränkungen handelt, da es stabiler und kontrollierbarer ist und auch weniger auf Online-Engineering angewiesen ist.

Die Pipeline des ersten Algorithmus-Frameworks ist in der folgenden Abbildung dargestellt. Zunächst werden Benutzermerkmale offline berechnet und dann ein Kausalmodell verwendet, um die Verbesserung der Kernindikatoren der Benutzer unter verschiedenen Strategien abzuschätzen, was den sogenannten Uplift darstellt. Basierend auf der geschätzten Verbesserung verwenden wir eine Mehrzieloptimierung, um die optimale Strategie zu lösen und zuzuweisen. Um die Berechnung des gesamten Prozesses zu beschleunigen, gruppieren wir die Menge im Voraus bei der Strukturierung. Dies bedeutet, dass wir davon ausgehen, dass die Personen in diesem Cluster dieselbe Ursache und Wirkung haben, und dementsprechend weisen wir der Gruppe dieselbe Strategie zu Personen im selben Cluster.

2. Strategieannahmen und Ursache-Wirkungs-Diagramm# 🎜🎜 #

Konzentrieren wir uns auf der Grundlage der obigen Diskussion darauf, wie die Strategie abstrahiert werden kann. Schauen wir uns zunächst an, wie wir das Kausaldiagramm abstrahieren. Die Ursache und Wirkung, die im Anreizszenario mit roten Umschlägen modelliert werden muss, spiegelt sich in mehreren Tagen und mehreren roten Umschlägen wider. Da der vorherige rote Umschlag definitiv Einfluss darauf hat, ob der nächste rote Umschlag empfangen wird, handelt es sich im Wesentlichen um ein Problem mit zeitlich variierenden Behandlungseffekten, das in einem Zeitreihen-Kausaldiagramm abstrahiert wird, wie rechts gezeigt.

Am Beispiel mehrerer roter Umschläge an einem Tag stellen alle Indizes von T eine Seriennummer des roten Umschlags dar. T stellt zu diesem Zeitpunkt einen Vektor dar, der aus der Menge des aktuellen roten Umschlags und dem Zeitintervall seit der Ausgabe des letzten roten Umschlags besteht. Y ist die aktuelle Nutzungszeit des Benutzers nach Ausgabe des roten Umschlags und die Erhöhung der Aufbewahrung am nächsten Tag. X ist die bis zum aktuellen Zeitpunkt beobachtete Störvariable, z. B. das Sehverhalten des Benutzers oder demografische Attribute usw. Natürlich gibt es viele unbeobachtete Störvariablen, die durch U dargestellt werden, wie etwa gelegentliche Aufenthalte oder gelegentliche Stopps der Benutzer. Eine wichtige unbeobachtete Störvariable ist die Denkweise des Benutzers, die hauptsächlich die Wertschätzung des Benutzers für die Menge der Anreize mit roten Umschlägen umfasst. Diese sogenannten Köpfe lassen sich nur schwer durch statistische Größen oder statistische Merkmale innerhalb des Systems darstellen.

Es wäre sehr kompliziert, die Red-Envelope-Strategie in Form von Zeitreihen zu modellieren, daher haben wir einige sinnvolle Vereinfachungen vorgenommen. Angenommen, U wirkt sich im aktuellen Moment nur auf T, X und Y aus und im nächsten Moment nur auf U, also auf den Geist des Benutzers. Das heißt, es wird sich nur auf das zukünftige Y auswirken, indem es die Wertbewertung oder Mentalität des nächsten Augenblicks beeinflusst. Aber selbst nach einer Reihe von Vereinfachungen werden wir feststellen, dass das gesamte Zeitreihen-Kausaldiagramm immer noch sehr dicht ist, was es schwierig macht, vernünftige Schätzungen vorzunehmen. Und wenn G-Methoden zur Lösung des zeitlich variierenden Trendeffekts verwendet werden, sind für das Training große Datenmengen erforderlich. In Wirklichkeit sind die Daten, die wir erhalten, jedoch sehr spärlich, sodass es schwierig ist, online einen guten Effekt zu erzielen. Am Ende haben wir viele Vereinfachungen vorgenommen und die Fork-Struktur (Fork) wie im Bild unten rechts erhalten. Wir haben eine Zusammenfassung aller Red-Envelope-Strategien für den Tag erstellt. Dabei handelt es sich um einen Vektor, der aus drei Elementen der Strategie besteht (Gesamtmenge der Red-Envelope-Anreize, Gesamtzeit und Gesamtzahl), dargestellt durch T. X ist eine Störvariable zum Zeitpunkt T-1, die das historische Verhalten und die demografischen Merkmale des Benutzers an diesem Tag darstellt. Y stellt die Nutzungszeit des Benutzers an diesem Tag dar. Dies ist der Indikator für die Aufbewahrungs- oder Nutzungszeit des Benutzers für den nächsten Tag. Obwohl diese Methode viele Details zu ignorieren scheint, beispielsweise die Interaktion zwischen roten Umschlägen. Aus makroökonomischer Sicht ist diese Strategie jedoch stabiler und ihre Auswirkungen können besser gemessen werden.

3. Strategiedarstellung und Kausalmodell#🎜🎜 #

Basierend auf der obigen Diskussion ist der nächste Schritt die Kernfrage, nämlich wie die Strategie (Behandlung) zum Ausdruck gebracht werden soll. Zuvor haben wir versucht, One-Hot zu verwenden, um die Vektoren mit drei Elementen unabhängig zu nummerieren, die drei Elemente zu trennen und die Zeitfunktion zu verwenden, um eine Behandlung mit mehreren Variablen zu erstellen. Die ersten beiden Strategien sind leichter zu verstehen und die letzte Methode wird als nächstes vorgestellt. Schauen Sie sich das Bild oben an. Wir haben die Sinusfunktionen der drei Elemente jeweils in Bezug auf t konstruiert, das heißt, bei gegebener Zeit T können wir jeweils die Menge, das Zeitintervall und die Anzahl erhalten. Wir verwenden die diesen Funktionen entsprechenden Parameter als Elemente des neuen Vektors, ähnlich der Darstellung der drei Elemente der Strategie. Unser Zweck, eine Funktion zum Ausdrücken der Strategie zu verwenden, besteht darin, mehr Details beizubehalten, da die ersten beiden Methoden die durchschnittliche Anzahl roter Hüllkurven und Verteilungsintervalle nur durch eine Kombination von Strategien ermitteln können und die Verwendung einer Funktion diese detaillierter darstellen kann. Allerdings führt diese Methode möglicherweise mehr Variablen ein und macht die Berechnung komplexer.

Nachdem die Strategie dargestellt ist, kann das Kausalmodell ausgewählt werden, um den Kausaleffekt abzuschätzen. In Form von One-Hot, das die drei Elemente von T darstellt, verwenden wir das x-Learner-Modell, um jede Strategie zu modellieren, und verwenden die Strategie mit dem kleinsten Gesamtbetrag als Basisstrategie, um den Behandlungseffekt aller Strategien zu berechnen und zu bewerten. In diesem Fall haben Sie möglicherweise das Gefühl, dass die Effizienz sehr gering ist und das Modell nicht verallgemeinert werden kann. Daher wenden wir weiterhin die gerade erwähnte dritte Strategie an, nämlich die Verwendung eines Vektors sinusförmiger Funktionselemente zur Bildung einer Behandlung. Als nächstes wird ein einzelnes DML-Modell verwendet, um die Leistung aller Strategien im Verhältnis zur Basisstrategie abzuschätzen. Darüber hinaus haben wir auch eine Optimierungs-DML erstellt und davon ausgegangen, dass y eine lineare Gewichtung der Störvariablen und des Kausaleffekts ist, dh y ist gleich dem Behandlungseffekt plus der Störvariablen. Auf diese Weise werden die Schnittterme und Terme höherer Ordnung zwischen Vektorelementen künstlich konstruiert. Dies entspricht der Konstruktion einer polynomialen Kernelfunktion zur Einführung nichtlinearer Funktionen. Auf dieser Basis hat sich DML im Vergleich zur Basisstrategie erheblich verbessert. Aus der Analyse der folgenden Abbildung können wir erkennen, dass das DML-Modell weniger Geld kostet und den ROI verbessert, was bedeutet, dass wir Ressourcen effizienter nutzen können.

Zuvor haben wir hauptsächlich einige Methodenabstraktionen und Modellentscheidungen besprochen. Im Übungsprozess werden wir auch einige voreingenommene Geschäftsprobleme finden, wie z als Behandlung bei One-Hot? Zu diesem Zeitpunkt haben wir eine Charge-für-Charge-Erweiterungsstrategie implementiert. Erstellen Sie zunächst eine Saatgutstrategie anhand der drei Elemente der Strategie, prüfen Sie dann manuell hochwertiges Saatgut, behalten Sie es bei und erweitern Sie es dann. Nach der Erweiterung werden wir neue Strategien stapelweise auf der Grundlage eines bestimmten Zeitraums einführen, beispielsweise in den ersten zwei Wochen nach der Einführung, und sicherstellen, dass die zufällige Traffic-Größe jeder Strategie konsistent oder vergleichbar ist. In diesem Prozess werden die Auswirkungen von Zeitfaktoren tatsächlich ignoriert und weniger wirksame Strategien werden kontinuierlich ersetzt, wodurch die Sammlung von Strategien bereichert wird. Darüber hinaus wird der Zeitfaktor definitiv Einfluss darauf haben, ob Zufallsverkehrsstrategien vergleichbar sind. Daher haben wir eine Methode entwickelt, die der Zeitscheibenrotation ähnelt, um sicherzustellen, dass die abgedeckten Zeitscheiben konsistent sind, wodurch der Einfluss von Zeitfaktoren auf die Strategie eliminiert wird, sodass der erhaltene zufällige Verkehr zum Trainieren des Modells verwendet werden kann.

Und wie generiert man neue Strategien? Eine einfache Methode ist die Verwendung der Grade-Suche oder des genetischen Algorithmus. Dies sind gebräuchlichere allgemeine Algorithmen für die Suche. Darüber hinaus können wir manuelles Beschneiden kombinieren, z. B. das Ausschneiden einiger unerwünschter Sequenztypen für rote Hüllkurven. Eine andere Methode besteht darin, BanditNet zu verwenden, eine Offline-Lernmethode zur Verstärkung, um unsichtbare Strategien zu berechnen, dh den kontrafaktischen Effekt abzuschätzen, und dann den geschätzten Wert zur Strategieauswahl zu verwenden. Natürlich müssen wir irgendwann den Online-Zufallsverkehr verwenden, um dies zu überprüfen. Der Grund dafür ist, dass die Varianz dieser Offline-Lernmethode wahrscheinlich sehr groß sein wird.

4. Strategische Probleme und Iteration

Zusätzlich zu den oben genannten Problemen werden wir auch auf einige teilweise geschäftliche Probleme stoßen . Die erste Frage ist, wie ist der Aktualisierungszyklus der Benutzerrichtlinien? Wäre es besser, wenn alle Benutzerrichtlinien regelmäßig aktualisiert würden? Diesbezüglich sind unsere praktischen Erfahrungen von Person zu Person unterschiedlich. Beispielsweise sollten sich Strategien für Hochfrequenznutzer langsamer ändern. Das liegt zum einen daran, dass Hochfrequenznutzer bereits mit unserem Format vertraut sind, einschließlich des Anreizbetrags. Wenn sich der rote Umschlagbetrag drastisch ändert, wird dies sicherlich Auswirkungen auf die entsprechenden Indikatoren haben. Daher pflegen wir eigentlich eine wöchentliche Update-Strategie für Hochfrequenzbenutzer und aktualisieren einmal pro Woche, aber für neue Benutzer ist der Update-Zyklus kürzer. Der Grund dafür ist, dass wir sehr wenig über neue Benutzer wissen und in der Lage sein möchten, geeignete Strategien schneller zu erkunden und schnell zu reagieren, um Strategieänderungen basierend auf Benutzerinteraktionen vorzunehmen. Da das Verhalten neuer Benutzer ebenfalls sehr spärlich ist, verwenden wir in diesem Fall die tägliche Ebene, um neue Benutzer oder einige Benutzer mit geringer Häufigkeit zu aktualisieren. Darüber hinaus müssen wir auch die Stabilität der Strategie überwachen, um die Auswirkungen von Funktionsrauschen zu vermeiden. Die von uns erstellte Pipeline ist rechts dargestellt. Hier überwachen wir, ob der Behandlungseffekt stabil ist, und wir überwachen auch täglich die vom Benutzer zugewiesene endgültige Strategie, z. B. den Unterschied zwischen der heutigen Strategie und der gestrigen Strategie, einschließlich Menge und Anzahl. Wir werden auch regelmäßig Schnappschüsse der Online-Strategie erstellen, hauptsächlich zum Debuggen und zur schnellen Wiedergabe, um die Stabilität der Strategie sicherzustellen. Darüber hinaus werden wir auch Experimente mit kleinem Verkehr durchführen und dessen Stabilität überwachen. Nur kleine Verkehrsexperimente, die die Stabilitätsanforderungen erfüllen, werden verwendet, um bestehende Strategien zu ersetzen.

Die zweite Frage ist, ob die Richtlinien für neue Benutzer und einige spezielle Benutzer unabhängig sind? Die Antwort lautet „Ja“. Neuen Benutzern bieten wir beispielsweise zunächst einen starken Anreiz, und dann lässt die Intensität des Anreizes mit der Zeit nach. Nachdem der Benutzer in den normalen Lebenszyklus eintritt, werden wir regelmäßige Anreizstrategien für ihn implementieren. Gleichzeitig wird es für besonders sensible Gruppen eine Mengenbeschränkung geben. Dazu werden wir auch unabhängige Modelle trainieren, um sich an diese Personengruppe anzupassen.

Die dritte Frage, die Sie sich vielleicht stellen, ist: Wie wichtig ist kausale Schlussfolgerung im gesamten Algorithmus-Framework? Aus theoretischer Sicht glauben wir, dass kausale Schlussfolgerungen von zentraler Bedeutung sind, da sie bei Anreizalgorithmen große Vorteile bringen. Im Vergleich zu Regressions- und Klassifizierungsmodellen steht die kausale Schlussfolgerung im Einklang mit den Geschäftszielen und ist von Natur aus ROI-orientiert, sodass sie Optimierungsziele hinsichtlich des Umfangs der Verbesserung mit sich bringt. Wir möchten jedoch alle daran erinnern, dass wir bei der Zuweisung von Budgets nicht für jeden Benutzer die optimale Strategie auswählen können und der kausale Effekt im Vergleich zu Einzelpersonen relativ gering ist. Wenn wir Budgets zuweisen, ist es sehr wahrscheinlich, dass einige Unterschiede in den kausalen Nutzereffekten beseitigt werden. Zu diesem Zeitpunkt wird unsere eingeschränkte Optimierung den Strategieeffekt stark beeinflussen. Daher haben wir beim Clustering auch weitere Clustering-Methoden ausprobiert, beispielsweise die Deep-Clustering-SCCL-Methode, um bessere Clustering-Ergebnisse zu erzielen. Wir haben auch einige Iterationen tiefgreifender Kausalmodelle wie BNN oder Dragonnet usw. durchgeführt.

Wir haben festgestellt, dass sich die Offline-Indikatoren des tiefen Kausalmodells in der Praxis zwar verbessert haben, seine Online-Wirkung jedoch nicht stabil ist genug. Der Hauptgrund ist das Auftreten fehlender Werte. Gleichzeitig haben wir auch festgestellt, dass die Feature-Planungsmethode einen großen Einfluss auf die Stabilität des Deep-Learning-Online-Modells hat, sodass wir letztendlich dazu neigen werden, die DML-Methode stabil zu verwenden.

So viel zu den Incentive-Szenarien, die ich gerne mit Ihnen teilen möchte das Angebot und die Nachfrage. Einige praktische und theoretische Untersuchungen von Tuning-Szenarien.

2. Kausale Schlussfolgerung und Anpassung von Angebot und Nachfrage

1. Geschäftshintergrund und Geschäftsmodellierung

Als Nächstes stellen wir einen Geschäftshintergrund von Tencent Microvision in Bezug auf Angebot und Nachfrage vor. Als Kurzvideoplattform bietet Weishi viele verschiedene Videokategorien. Für Benutzergruppen mit manchmal unterschiedlichen Sehinteressen müssen wir den Expositionsanteil oder den Inventaranteil jeder Kategorie entsprechend den unterschiedlichen Benutzermerkmalen angemessen zuweisen. Das Ziel besteht darin, die Benutzererfahrung und die Benutzerbetrachtungszeit zu verbessern, unter denen die Erfahrung des Benutzers liegen kann gemessen anhand der 3-Sekunden-Schnellwischgeschwindigkeitsanzeige, und die Betrachtungszeit wird hauptsächlich anhand der Gesamtwiedergabezeit gemessen. Wie kann ich das Belichtungsverhältnis oder das Inventarverhältnis von Videokategorien anpassen? Die Hauptmethode, die wir in Betracht ziehen, besteht darin, einige Kategorien proportional zu erhöhen oder zu verringern. Das Verhältnis von Anstieg und Rückgang ist ein voreingestellter Wert.

Als nächstes müssen wir mithilfe von Algorithmen bestimmen, wie wir entscheiden, welche Kategorien erhöht und welche verringert werden sollen, um das Benutzererlebnis und die Anzeigezeit zu maximieren. Gleichzeitig müssen wir einige Einschränkungen erfüllen, z als Gesamtexpositionsgrenzwerte. Dieser Ort fasst drei Hauptmodellierungsideen zusammen. Die erste ist eine einfachere Idee, das heißt, wir behandeln die Zunahme und Abnahme direkt als Behandlungsvariable von 0 und 1, schätzen ihre kausale Wirkung und führen dann eine eingeschränkte Optimierung mit mehreren Zielen durch, um eine endgültige Strategie zu erhalten. Die zweite Idee besteht darin, die Behandlung genauer zu modellieren. Wir behandeln die Behandlung als kontinuierliche Variable. Beispielsweise ist das Expositionsverhältnis einer Kategorie eine Variable, die sich kontinuierlich zwischen 0 und 1 ändert. Passen Sie dann eine entsprechende Kausaleffektkurve oder Kausaleffektfunktion an, führen Sie dann eine Optimierung mit mehreren Zielen durch und erhalten Sie schließlich die endgültige Strategie. Es ist zu beachten, dass es sich bei den beiden gerade genannten Methoden um zweistufige Methoden handelt. Die dritte Idee: Wir bringen Einschränkungen in die Schätzung der kausalen Effekte ein und erhalten so eine optimale Strategie, die die Einschränkungen erfüllt. Dies ist auch der Forschungsinhalt, den ich später mit Ihnen teilen möchte.

Konzentrieren wir uns zunächst auf die ersten beiden Modellierungsideen. Es gibt mehrere Modellierungspunkte, die beachtet werden müssen. Der erste Punkt besteht darin, dass wir zur Gewährleistung der Genauigkeit der Schätzung des kausalen Effekts die Population aufteilen und den kausalen Effekt der binären Behandlung oder kontinuierlichen Behandlung auf jede Population abschätzen müssen. Gerade hat Lehrer Zheng auch Methoden zur Klassifizierung von Personen erwähnt, beispielsweise die Verwendung von Kmeans-Clustering oder einem tiefen Clustering. Der zweite Punkt ist die Bewertung des Modelleffekts auf nicht zufällige experimentelle Daten. Beispielsweise müssen wir die Wirkung des Modells offline bewerten, ohne einen AB-Test durchzuführen. Zu diesem Thema können Sie auf einige Indikatoren zurückgreifen, die in dem oben indexierten Dokument zum PPT für die Offline-Bewertung erwähnt sind. Der dritte zu beachtende Punkt ist, dass wir die Korrelation und gegenseitige Beeinflussung zwischen Kategorien so weit wie möglich berücksichtigen sollten, wie z. B. einige Probleme der Verdrängung zwischen ähnlichen Kategorien usw. Wenn diese Faktoren in die Abschätzung der kausalen Wirkungen einbezogen werden können, sollten bessere Ergebnisse erzielt werden.

2. Strategie zur Anpassung des Belichtungsanteils einer einzelnen Gruppe

Als nächstes werden wir diese Modellierungsideen im Detail entwickeln. Die erste Modellierungsmethode besteht zunächst darin, eine Behandlung von 0 und 1 zu definieren, die verwendet wird, um die Mittel zur Erhöhung oder Verringerung dieser beiden Interventionstypen darzustellen. Sie können sich auf das kurze Ursache-Wirkungs-Diagramm auf der linken Seite beziehen , wobei x einige Merkmale des Benutzers darstellt, wie z. B. relevante statistische Merkmale sowie andere Benutzerattribute usw. y ist das Ziel, das uns wichtig ist, nämlich die Beschleunigungsrate von 3 Sekunden oder die Gesamtwiedergabezeit. Darüber hinaus ist es auch notwendig, auf einige unbeobachtete Störvariablen zu achten, wie z. B. versehentliches, schnelles Wischen und Verlassen des Benutzers, und derselbe Benutzer kann tatsächlich von mehreren Personen verwendet werden, was ebenfalls ein Problem mehrerer Benutzeridentitäten darstellt. Darüber hinaus wird sich die kontinuierliche Iteration und Aktualisierung der Empfehlungsstrategie auch auf die Beobachtungsdaten auswirken, und die Migration von Benutzerinteressen liegt ebenfalls außerhalb der Beobachtung. Diese unbeobachteten Störvariablen können die Schätzung der kausalen Effekte bis zu einem gewissen Grad beeinflussen.

Für diese Art der Modellierung können gängige Methoden zur Schätzung kausaler Effekte gelöst werden. Sie können beispielsweise T-Learner oder X-Learner oder DML in Betracht ziehen, die kausale Auswirkungen abschätzen können. Natürlich weist diese einfache Modellierungsmethode auch einige Probleme auf. Wenn wir beispielsweise die binäre Behandlung zur Modellierung verwenden, wird sie zu vereinfacht. Darüber hinaus wird bei dieser Methode jede Kategorie separat betrachtet und die Korrelation zwischen den Kategorien wird nicht berücksichtigt. Das letzte Problem besteht darin, dass wir bestimmte Faktoren wie die Reihenfolge der Belichtung und die Qualität des Inhalts in der gesamten Frage nicht berücksichtigt haben.

Als nächstes stellen wir die zweite Modellierungsidee vor. Wir betrachten alle Kategorien zusammen. Wir haben beispielsweise k Videokategorien und lassen die Behandlung einen k-dimensionalen Ursachenvektor sein. Jede Position des Vektors stellt eine Kategorie dar, beispielsweise Film- und Fernsehvarietés oder MOBA-Events usw. 0 und 1 stehen immer noch für Erhöhungen oder Verringerungen. Zu diesem Zeitpunkt kann die Schätzung des kausalen Effekts der Behandlung in mehrdimensionalen Vektoren durch den DML-Algorithmus gelöst werden. Normalerweise behandeln wir den Behandlungsvektor, der alle 0 ist, als Kontrolle. Obwohl diese Methode das Problem löst, dass nicht jede Kategorie separat betrachtet wird, weist sie dennoch einige potenzielle Probleme auf. Das erste ist das Problem der Dimensionsexplosion, die durch zu viele Kategorien verursacht wird. Da es an jeder Position zwei Situationen mit 0 und 1 gibt, nimmt die Anzahl möglicher Permutationen und Kombinationen exponentiell zu, was sich auf Ursache und Wirkung auswirkt . Die Genauigkeit der Effektschätzungen führt zu Interferenzen. Darüber hinaus werden Faktoren wie die zuvor erwähnte Belichtungsreihenfolge und der Inhalt nicht berücksichtigt.

Nachdem wir die Modellierungsideen der binären Variablenbehandlung geteilt haben, können wir als nächstes die Behandlung detaillierter modellieren, die ihren eigenen Merkmalen besser entspricht. Wir haben festgestellt, dass das Belichtungsverhältnis selbst eine kontinuierliche Variable ist, sodass es für uns sinnvoller ist, für die Modellierung eine kontinuierliche Behandlung zu verwenden. Bei dieser Modellierungsidee müssen wir zunächst die Masse aufteilen. Für jede Personengruppe modellieren wir jede Kategorie separat, um eine Kausalwirkungskurve einer einzelnen Gruppe*einzelnen Kategorie zu erhalten. Wie im Bild links dargestellt, stellt die Kausaleffektkurve die Auswirkung des Anteils verschiedener Kategorien auf die Ziele dar, die uns am Herzen liegen. Um eine solche kausale Wirkungskurve abzuschätzen, teile ich hauptsächlich zwei mögliche Algorithmen, einen ist DR-Net und der andere ist VC-Net. Beide Algorithmen gehören zur Kategorie des tiefen Lernens. Der Aufbau des Modells ist wie im Bild rechts dargestellt.

Stellen Sie zunächst DR-Net vor. Die Eingabe x des Modells durchläuft zunächst mehrere vollständig verbundene Schichten, um eine implizite Darstellung namens z zu erhalten. DR-Net verwendet eine Diskretisierungsstrategie, die die kontinuierliche Behandlung in mehrere Blöcke unterteilt und dann jeder Block ein Subnetzwerk trainiert, um die Zielvariable vorherzusagen. Da DR-Net eine Diskretisierungsstrategie anwendet, ist die endgültige Kausaleffektkurve, die es erhält, nicht streng kontinuierlich, aber je dünner die Diskretisierung wird, desto näher kommt die endgültige Schätzung einer kontinuierlichen Kurve. Je dünner die idealisierte Segmentierung wird, desto mehr Parameter bringt sie natürlich mit sich und das Risiko einer Überanpassung steigt.

Als nächstes werde ich über VC-Net berichten. VC-Net verbessert bis zu einem gewissen Grad die Mängel von DR-Net. Zunächst einmal ist die Eingabe des VC-Net-Modells immer noch X, was auch das Merkmal des Benutzers ist. Es erhält auch erst nach mehreren vollständig verbundenen Schichten eine implizite Darstellung Z. Bei Z wird jedoch zunächst ein Modul zur Vorhersage des Propensity Score angeschlossen. Unter kontinuierlichen Behandlungsbedingungen ist die Neigung eine Wahrscheinlichkeitsdichte der Behandlung t unter einer gegebenen X-Bedingung, die in der Abbildung auch durch π dargestellt wird. Schauen wir uns als Nächstes die Netzwerkstruktur nach Z an. Im Gegensatz zur Diskretisierungsoperation von DR-Net verwendet VC-Net eine Netzwerkstruktur mit variablen Koeffizienten, dh jeder Modellparameter nach Z ist ein Parameter der t-Funktion. Die Autoren der hier erwähnten Literatur verwendeten die Basisfunktionsmethode, um jede Funktion als lineare Kombination von Basisfunktionen auszudrücken, die auch als θ(t) geschrieben wird. Auf diese Weise wird die Schätzung der Funktion zur Parameterschätzung der Linearkombination der Basisfunktionen. Auf diese Weise stellt die Parameteroptimierung des Modells kein Problem dar und die von VC-Net erhaltene Kausaleffektkurve ist ebenfalls eine kontinuierliche Kurve. Die von VC-Net zu lösende Zielfunktion besteht aus mehreren Teilen. Einerseits besteht es aus dem quadratischen Verlust der endgültigen Vorhersage am Ziel, der in der Abbildung μ beträgt. Andererseits besteht es auch aus dem logarithmischen Verlust der Wahrscheinlichkeitsdichte der Neigung. Zusätzlich zu diesen beiden Teilen fügt der Autor der Zielfunktion auch einen Strafterm namens gezielte Regularisierung hinzu, sodass doppelt robuste Schätzeigenschaften erhalten werden können. Für spezifische Details können interessierte Freunde auf die beiden oben indizierten Originalpapiere verweisen.

Lassen Sie uns zum Schluss den Weg für einen Teil unserer Forschung ebnen, den wir bald mit Ihnen teilen werden. Wir haben festgestellt, dass der Belichtungsanteil jeder Videokategorie ein mehrdimensionaler kontinuierlicher Vektor ist. Der Grund für die Mehrdimensionalität liegt darin, dass wir mehrere Videokategorien haben und jede Dimension eine Videokategorie darstellt. Der Hauptgrund für die Kontinuität besteht darin, dass der Belichtungsanteil jeder Videokategorie kontinuierlich ist und seine Werte zwischen 0 und 1 liegen. Gleichzeitig gibt es eine natürliche Einschränkung, nämlich dass das Gesamtbelichtungsverhältnis aller unserer Videokategorien gleich 1 sein muss. Daher können wir einen solchen mehrdimensionalen kontinuierlichen Vektor als Behandlung betrachten.

Der rechts abgebildete Vektor ist ein Beispiel dafür. Unser Ziel ist es, das optimale Belichtungsverhältnis zu finden, um unsere Gesamtspielzeit zu maximieren. Im traditionellen Kausalrahmen ist es für Algorithmen schwierig, ein derart mehrdimensionales, kontinuierliches und uneingeschränktes Problem zu lösen. Als nächstes teilen wir unsere Forschung zu diesem Thema.

3. Teilen des Constrained Continuous Multivariable Causal Model

MDPP Forest Diese Arbeit ist eine Methodenerkundung und innovative Lösung für das Problem, das das Team bei der Untersuchung von Angebots- und Nachfrageproblemen durchgeführt hat. Unser Team stellte damals fest, dass angesichts des Problems, wie man jedem Benutzer das beste Videokategorie-Belichtungsverhältnis zuordnen kann, andere bestehende gängige Methoden kein Ergebnis erzielen konnten, das besser den Erwartungen entsprach. Daher kann die von unserem Team entwickelte Methode nach einer Test- und Verbesserungsphase offline gute Ergebnisse erzielen, dann mit Empfehlungen zusammenarbeiten und schließlich bestimmte strategische Vorteile erzielen. Diese Arbeit haben wir dann zu einem Papier zusammengefasst, das glücklicherweise auf KDD 2022 veröffentlicht werden konnte.

1. Hintergrund und Herausforderungen

Stellen Sie zunächst den Hintergrund des Problems vor. Im Hinblick auf Angebot und Nachfrage unterteilen wir Kurzvideos je nach Inhalt in verschiedene Kategorien, z. B. Populärwissenschaft, Film und Fernsehen, Essen im Freien usw. Das Videokategorie-Belichtungsverhältnis bezieht sich auf den Anteil jeder dieser verschiedenen Videokategorien an allen von einem Benutzer angesehenen Videos. Benutzer haben sehr unterschiedliche Präferenzen für verschiedene Kategorien und Plattformen müssen oft von Fall zu Fall das optimale Belichtungsverhältnis für jede Kategorie ermitteln. In der Neuordnungsphase wird die Empfehlung verschiedener Videotypen gesteuert. Eine große Herausforderung für das Unternehmen besteht darin, das beste Verhältnis der Videobelichtungen zuzuweisen, um die Zeit jedes Benutzers auf der Plattform zu maximieren.

Die Hauptschwierigkeit eines solchen Problems liegt in den folgenden drei Punkten. Der erste Grund besteht darin, dass im Kurzvideo-Empfehlungssystem die Videos, die jeder Benutzer sieht, eine sehr starke Korrelation mit seinen eigenen Eigenschaften aufweisen. Dies ist eine selektive Tendenz. Daher müssen wir Algorithmen im Zusammenhang mit kausalen Schlussfolgerungen verwenden, um Verzerrungen zu beseitigen. Zweitens ist das Belichtungsverhältnis der Videokategorie eine kontinuierliche, mehrdimensionale und eingeschränkte Behandlung. Derzeit gibt es für solch komplexe Probleme in den Bereichen kausale Schlussfolgerung und Politikoptimierung keine sehr ausgereiften Methoden. Der dritte Grund ist, dass wir bei Offline-Daten nicht a priori das wirklich optimale Expositionsverhältnis jeder Person kennen können, sodass es schwierig ist, diese Methode zu bewerten. In einer realen Umgebung handelt es sich lediglich um einen Unterlink zur Empfehlung. Die endgültigen experimentellen Ergebnisse können die Genauigkeit dieser Methode für ihre eigenen Berechnungsziele nicht beurteilen. Daher ist es für uns schwierig, das Problem dieses Szenarios genau einzuschätzen. Wir werden später vorstellen, wie wir die Wirkungsbewertung durchführen.

2. Problemdefinition

Wir abstrahieren die Daten zunächst in ein Kausaldiagramm in der Statistik. Darunter Vektor. Y ist die Betrachtungszeit des Benutzers, also die Reaktion auf das Aufgabenziel. Das Ziel unserer Modellierung besteht darin, unter bestimmten Benutzereigenschaften Dieses Problem scheint einfach durch ein kausales ternäres Diagramm dargestellt zu werden, aber es gibt ein großes Problem, das bereits erwähnt wurde. Unsere Behandlung besteht darin, das Expositionsverhältnis mehrerer Kategorien zu berücksichtigen und einen mehrdimensionalen Vektor zu konstruieren mit kontinuierlichen Werten und die Summe der Vektoren ist 1. Dieses Problem ist komplizierter.

3. Methodeneinführung - Maximum Difference Point of Preference (MDP2) Forest

In dieser Hinsicht basiert unsere Methode auch auf dem Kausalentscheidungswald (Kausalwald). Allgemeine kausale Entscheidungsbäume können Behandlungsprobleme nur mit eindimensionalen diskreten Werten lösen. Durch die Verbesserung der Berechnung der Zwischenaufteilungskriteriumsfunktion fügen wir während der Aufteilung einige hochdimensionale kontinuierliche Informationen hinzu, sodass das Problem hochdimensionaler kontinuierlicher Werte und eingeschränkter Behandlung gelöst werden kann.

① Einführung in die Methode – Dauerbehandlungsproblem

Zunächst lösen wir das Dauerbehandlungsproblem. Wie in der Abbildung gezeigt, ist die Wirkung von T auf Y eine kontinuierliche Kurve. Nehmen wir zunächst an, dass es sich um eine monoton steigende Kurve handelt. Für alle Behandlungswerte in den Daten durchlaufen wir diese und berechnen den Y-Mittelwert der linken und rechten Stichprobe, um den Punkt mit der größten Differenz zwischen dem Y-Mittelwert links und dem Y-Mittelwert rechts zu finden, d. h. der Punkt mit dem größten durchschnittlichen kausalen Nutzen. Wir nennen diesen Punkt den Punkt der maximalen Differenz, der der effizienteste Punkt im kontinuierlichen Behandlungsbereich ist, was bedeutet, dass die Behandlung Y erheblich verändern kann. Der maximale Differenzpunkt ist der Punkt, den wir in einer einzelnen Dimension erhalten möchten.

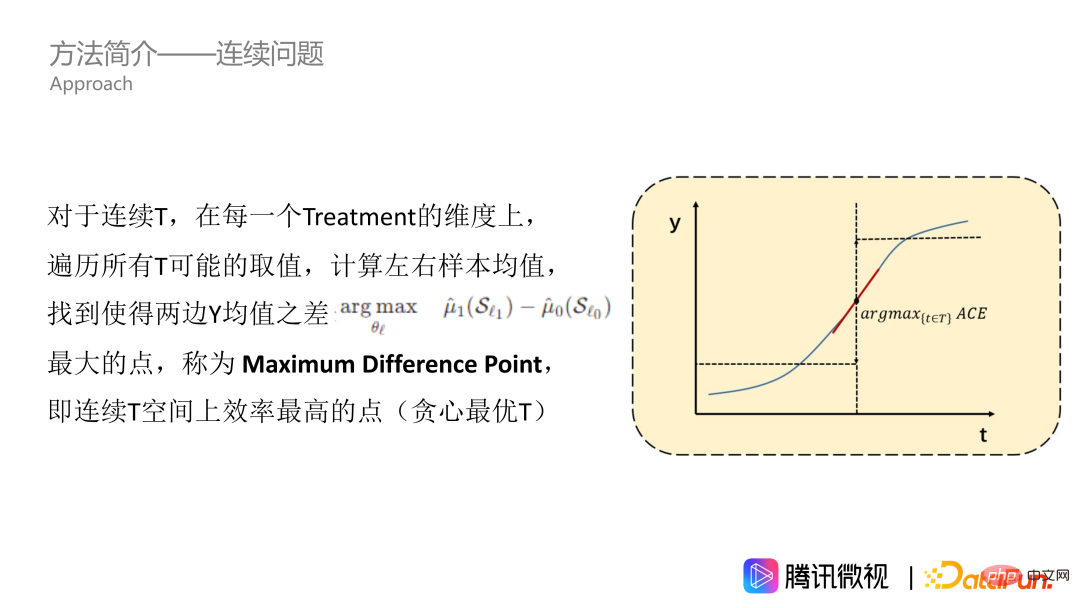
Die eben genannte Methode eignet sich jedoch nur für monoton ansteigende Kurven. Tatsächlich sind die meisten Probleme jedoch nicht so gut, insbesondere die Frage des Belichtungsverhältnisses. Bei diesem Thema verläuft die Wirkungskurve im Allgemeinen bergförmig, das heißt, sie steigt zuerst an und fällt dann ab. Das Empfehlen von mehr Videos, die den Benutzern gefallen, kann die Betrachtungszeit der Benutzer verlängern. Wenn dieser Typ jedoch zu oft empfohlen wird, wird die gesamte Videoempfehlung sehr eintönig und langweilig und verdrängt auch den Belichtungsraum der Videotypen, die andere Benutzer haben wie. Die Kurve ist also im Allgemeinen bergförmig, kann aber auch andere Formen haben. Um uns an die T-Kurve beliebiger Form anzupassen, müssen wir eine Integraloperation durchführen, dh das Wertebereichsintervall für die Akkumulation ermitteln. Auf der akkumulierten Kurve berechnen wir auch die Mittelwerte auf der linken und rechten Seite sowie den Punkt, an dem die Differenz zwischen den Mittelwerten auf den beiden Seiten am größten ist, z. B. den fünfzackigen Stern in das Bild. Dieser Punkt kann als maximaler Differenzpunkt der Präferenz bezeichnet werden, der unser MDPP ist.

② Einführung in die Methode – hochdimensionales Problem #🎜 🎜#

Oben haben wir vorgestellt, wie das kontinuierliche Problem gelöst werden kann. Die gerade erwähnte Kurve ist nur eindimensional und entspricht einer einzelnen Videokategorie. Als nächstes verwenden wir die Idee der heuristischen Dimensionsdurchquerung, um mehrdimensionale Probleme zu lösen. Bei der Berechnung des Klassifizierungswerts verwenden wir eine heuristische Idee, um die K-Dimensionen zufällig zu sortieren und eine Aggregation von D-Indikatoren in jeder Dimension zu berechnen, d. h. eine Summationsoperation durchzuführen. Erhalten Sie D* als hochdimensionale Informationsentropie und berücksichtigen Sie dann die Einschränkung. Die Einschränkung besteht darin, dass die Summe aller MDPPs 1 ist. Hier müssen wir die folgenden zwei Situationen berücksichtigen. Eine davon ist, dass die Summe von MDPP nach dem Durchlaufen der K-Dimension nicht 1 erreicht. Als Reaktion auf diese Situation addieren wir die Summe aller MDPPs und normalisieren sie auf 1. Der zweite Fall ist, dass die Summe von MDPP 1 erreicht hat, wenn wir nur die K'-Dimension durchlaufen, die kleiner als die K-Dimension ist. Dazu stoppen wir die Durchquerung und setzen den MDPP auf die verbleibende „Ressourcenmenge“, also 1 minus der Summe der zuvor berechneten MDPP-Werte, damit die Einschränkungen berücksichtigt werden können.

Darüber hinaus werden wir auch Der Begriff „Wald“ wird in die obige Baumstruktur eingeführt, da er zwei Hauptbedeutungen hat. Die erste ist unsere traditionelle Idee des Bagging-Ensembles, bei der mehrere Lernende eingesetzt werden können, um die Robustheit des Modells zu verbessern. Der zweite Grund ist, dass bei der Dimensionsdurchquerung jedes Mal, wenn ein Knoten geteilt wird, nur K‘-Dimensionen berechnet werden und einige Dimensionen nicht enthalten sind. Damit jede Dimension die gleiche Chance hat, an der Aufteilung teilzunehmen, müssen wir mehrere Bäume erstellen.

③ Methodeneinführung - Algorithmusbeschleunigung#🎜🎜 #

Da der Algorithmus drei Durchquerungsebenen enthält, erfordern alle Baummodelle eine Eigenwertdurchquerung sowie eine zusätzliche Dimensionsdurchquerung und Suchdurchquerung von MDPP. Eine solche dreischichtige Durchquerung macht die Effizienz sehr gering. Daher verwenden wir die Methode des gewichteten Quantilgraphen für die Eigenwertdurchquerung und die MDPP-Durchquerung und berechnen die entsprechenden Ergebnisse nur an den Quantilpunkten, was die Komplexität des Algorithmus erheblich reduzieren kann. Gleichzeitig haben wir festgestellt, dass diese Quantilpunkte auch die Grenzpunkte des „kumulativen Wertebereichs“ sind, was den Rechen- und Speicheraufwand erheblich reduzieren kann. Unter der Annahme, dass es q-Quantile gibt, müssen wir nur q-mal berechnen, um die Anzahl der Stichproben und den Mittelwert von y in jedem Quantilintervall zu erhalten. Auf diese Weise berechnen wir jedes Mal die Differenz d zwischen den Mittelwerten auf beiden Seiten Sie müssen den q-Wert durch die beiden Teile auf der rechten Seite teilen. Führen Sie einfach eine gewichtete Summe der Durchschnittswerte in jedem Intervall durch. Wir müssen den Mittelwert aller Stichproben links und rechts vom Quantilpunkt nicht mehr neu berechnen. Kommen wir weiter unten zum experimentellen Teil.

4. Experimentelles Design

① Experimentelles Design-Metrik

# 🎜🎜#Unsere experimentelle Bewertung ist im Wesentlichen ein Strategiebewertungsproblem, daher haben wir Indikatoren für die Strategiebewertung eingeführt. Der erste ist der Main Regret, der die Lücke zwischen der Rendite der Gesamtstrategie und der theoretisch optimalen Rendite misst. Der andere ist der Hauptbehandlungsquadratfehler, der verwendet wird, um die Lücke zwischen dem geschätzten Wert und dem optimalen Wert jeder Behandlungsdimension bei mehrdimensionaler Behandlung zu messen. Für beide Indikatoren gilt: je kleiner, desto besser. Das größte Problem bei der Festlegung dieser beiden Bewertungsindikatoren besteht jedoch darin, den optimalen Wert zu ermitteln.

② Experimentelles Design – Vergleichsmethode

Stellen wir unsere Vergleichsmethode vor. Erstens gibt es zwei häufig verwendete Methoden für kausale Schlussfolgerungen, eine ist DML mit vollständiger statistischer Theorie und die andere ist das Netzwerkmodell DR-Net und VC-Net. Diese Methoden können nur eindimensionale Probleme behandeln. Für das Problem in diesem Artikel haben wir jedoch einige Anpassungen vorgenommen, um mehrdimensionale Probleme zu lösen, dh zuerst den Absolutwert jeder Dimension zu berechnen und dann eine Normalisierung durchzuführen. In den folgenden beiden Artikeln gibt es auch Methoden zur Strategieoptimierung, die wir OPE und OCMD nennen. In diesen beiden Artikeln heißt es, dass ihre Methoden für mehrdimensionale Probleme geeignet sind, sie weisen jedoch auch darauf hin, dass es für diese Methoden schwierig ist, effektiv zu sein, wenn zu viele Dimensionen vorhanden sind.

③ Experimenteller Design-Simulations-Datensatz#🎜🎜 #

Um die Modelleffekte einfach und direkt vergleichen zu können, haben wir reale Probleme simuliert und eine vereinfachte Version des Simulationsdatensatzes generiert. Der Merkmalsraum x repräsentiert 6 Dimensionen von Benutzermerkmalen und 2 Verhaltensmerkmale. Für Proben mit unterschiedlichen Eigenschaften gehen wir zunächst von der optimalen Strategie aus. Wie in der Abbildung gezeigt, ist beispielsweise ein Benutzer, der jünger als 45 Jahre ist, einen Bildungsgrad von mehr als 2 und ein Verhaltensmerkmal von mehr als 0,5 hat, der Beste in 6 Videokategorien. Generieren Sie mithilfe der Formel auf der linken Seite zunächst zufällig eine Expositionsstrategie für Benutzer und berechnen Sie dann die Lücke zwischen der Expositionsstrategie und der tatsächlich optimalen Strategie sowie die Dauer simulierter Benutzer. Wenn die Strategie näher an der optimalen Strategie des Benutzers liegt, ist die Dauer y des Benutzers länger. Auf diese Weise haben wir einen solchen Datensatz generiert. Der Vorteil dieses simulierten Datensatzes besteht darin, dass wir direkt den optimalen Wert annehmen, was für die Auswertung sehr praktisch ist. Zum anderen sind die Daten relativ einfach, was es uns erleichtert, die Ergebnisse des Algorithmus zu analysieren. Werfen wir einen Blick auf den simulierten Datensatz. Die oben genannten experimentellen Ergebnisse bieten verschiedene Methoden zur Berechnung des Mittelwerts der entsprechenden Behandlung für den gerade genannten Personentyp. Die erste Zeile ist das theoretische Optimum, die zweite Zeile ist unser MDPP-Forest und die dritte Zeile basiert auf der MDPP-Forest-Methode, die dem Aufteilungskriterium einige Strafterme hinzufügt. Es ist ersichtlich, dass die Lücke zwischen unserer Methode und dem theoretischen Optimum sehr gering sein wird. Die anderen Methoden sind nicht besonders extrem, aber relativ gleichmäßig. Darüber hinaus haben unsere beiden Methoden anhand der MR- und MTSE-Abbildungen auf der rechten Seite auch ganz offensichtliche Vorteile.

④ Experimentelles Design – halbsynthetischer Datensatz

Neben simulierten Datensätzen verwenden wir auch reale Geschäftsdaten Es wurden halbsynthetische Daten erstellt. Die Daten stammen von der Tencent Weishi-Plattform. Xi repräsentiert die 20-dimensionalen Eigenschaften des Benutzers, Behandlung ti repräsentiert das mehrdimensionale Videokategorie-Belichtungsverhältnis, das einen 10-dimensionalen Vektor bildet, und yi (ti) repräsentiert die Nutzungszeit des i-ten Benutzers. Ein Merkmal tatsächlicher Szenarien besteht darin, dass wir das wirklich optimale Videobelichtungsverhältnis des Benutzers nicht kennen können. Daher erstellen wir eine Funktion gemäß den Regeln des Clusterzentrums und generieren ein virtuelles y, um das reale y zu ersetzen, sodass das y der Stichprobe eine bessere Regelmäßigkeit aufweist. Ich werde hier nicht näher auf die konkrete Formel eingehen. Interessierte Studierende können den Originaltext lesen. Warum ist das möglich? Denn der Schlüssel zu unserem Algorithmus liegt darin, dass er in der Lage sein muss, einige verwirrende Effekte zwischen x und t aufzulösen, was bedeutet, dass Online-Benutzer von voreingenommenen Strategien betroffen sind. Um die Wirkung der Strategie zu bewerten, behalten wir nur x und t bei und ändern y, um das Problem besser bewerten zu können. Bei halbsynthetischen Daten ist die Wirkung unseres Algorithmus ebenfalls deutlich besser und der Vorteil wird größer sein als bei dem simulierten Datensatz. Dies zeigt, dass unser MDPP-Forests-Algorithmus stabiler ist, wenn die Daten komplex sind. Werfen wir außerdem einen Blick auf die Hyperparameter synthetischer Daten, nämlich die Größe der Gesamtstruktur. Im Bild unten rechts können wir sehen, dass mit zunehmender Waldgröße die Indikatoren unter den beiden Aufteilungskriterien immer besser konvergieren und bei 100 Bäumen besser sind Der optimale Effekt wird mit 250 Bäumen erreicht, und dann kommt es zu einer gewissen Überanpassung. #🎜🎜 ## 🎜🎜 ## 🎜🎜 ## 🎜🎜 ## 🎜🎜 ## 🎜🎜 ## 🎜🎜 ## 🎜🎜 ## 🎜🎜 ## 🎜🎜#4. Q & A -Sitzung#🎜🎜 ## 🎜 🎜#F: Warum kann die Normalisierung funktionieren, wenn die Durchquerungsexposition 1 überschreitet?

A: Mein Verständnis ist das, denn was wir tun, ist eine Optimierung der Expositionsanteilsbeschränkungen. In diesem Prozess sind wir relativ wertvoll. Beim Durchqueren suchen wir nach dem optimalen Teilungspunkt und finden heraus, welcher Kategorie Priorität eingeräumt werden sollte, um mehr Aufmerksamkeit zu erzielen. Solange wir in diesem Prozess sicherstellen können, dass er proportional skaliert wird, ist das in Ordnung.

Ich habe die gleiche Ansicht, nur die proportionale Skalierung ist in Ordnung. Da 1 eine starke Einschränkung darstellt, wird der von uns zu Beginn berechnete Wert definitiv nicht genau 1 sein, sondern niedriger oder höher sein. Wenn es viel mehr gibt, gibt es keine Möglichkeit, die einzigartige Bedingung starker Einschränkungen zu erfüllen, und es ist natürlicher, ein normalisiertes Denken zu verwenden. Weil wir das relative Größenverhältnis zwischen den einzelnen Kategorien berücksichtigen. Ich denke, das relative Größenverhältnis ist wichtiger als eine Frage des absoluten Wertes.

Das obige ist der detaillierte Inhalt vonAnwendung kausaler Schlussfolgerungen in Micro-View-Anreizen und Angebots- und Nachfrageszenarien. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!