So finden Sie den nächsten gemeinsamen Vorfahren eines Binärbaums in Java

Idee 1: Nehmen Sie zunächst an, dass dieser Baum ein binärer Suchbaum ist.

Fügen wir zunächst eine ergänzende Erklärung hinzu, was ein binärer Suchbaum ist: ​​​​im rechten Teilbaum sind alle kleiner als er, und die Werte im rechten Teilbaum sind größer als er. Das Durchlaufen eines binären Suchbaums in der Reihenfolge ist also ein geordneter Datensatz.

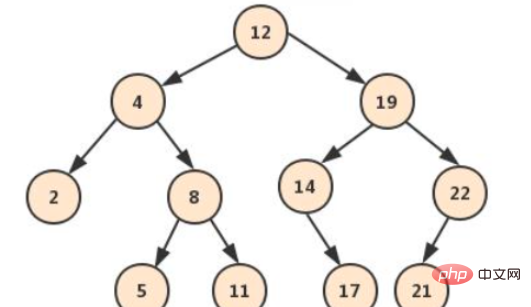Für den obigen Baum wird davon ausgegangen, dass der jüngste gemeinsame Vorfahre von p q erforderlich ist.

Dann gibt es die folgenden Situationen:

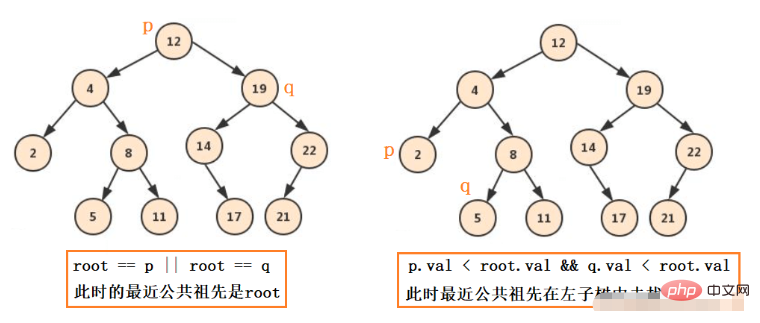
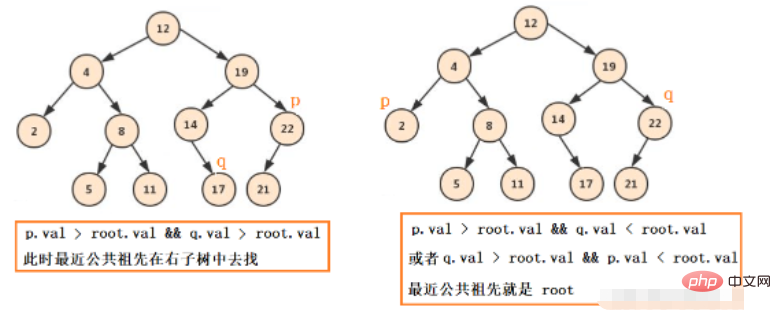Für gewöhnliche Binärbäume gibt es nichts weiter als diese Situationen: pq ist links, pq ist rechts, pq ist links und einer weiter Das rechte, pq hat einen, der der Wurzelknoten ist.

Gehen Sie also rekursiv zum linken Teilbaum und zum rechten Teilbaum, um den gemeinsamen Vorfahren des p q-Knotens zu finden. Wenn er nicht gefunden wird, wird er leer zurückgegeben.

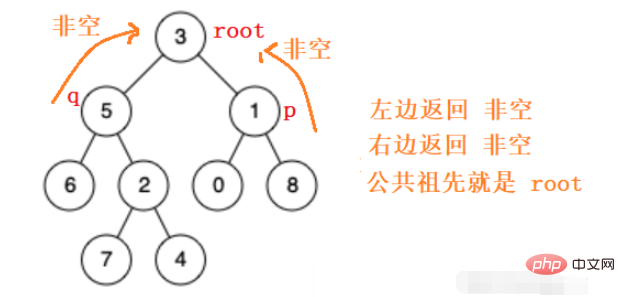
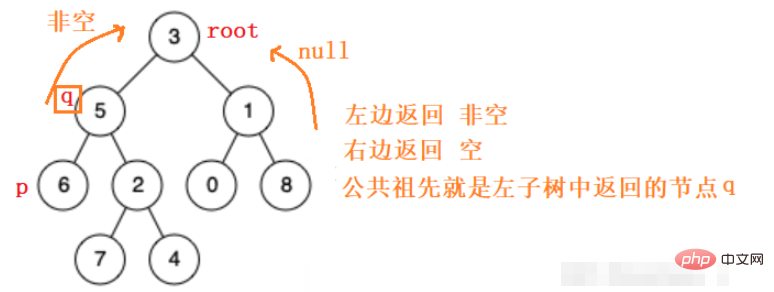
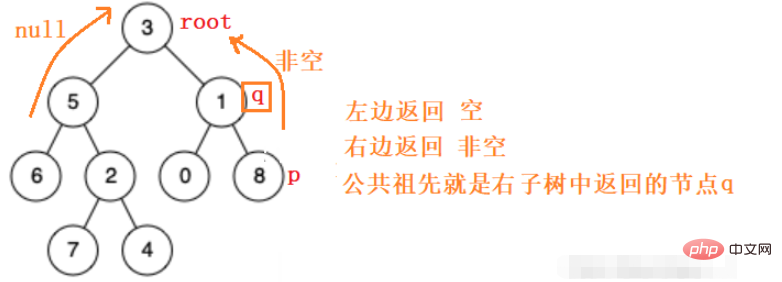Gemäß den obigen Ideen können wir den Code einfach schreiben

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    if(root == null) return null;

    // p 为当前树的根节点
    if(p == root) return p;
    // q 为当前树的根节点
    if(q == root) return q;
    
    // 去左子树中找
    TreeNode left = lowestCommonAncestor(root.left,p,q);
    // 去右子树中找
    TreeNode right = lowestCommonAncestor(root.right,p,q);

    // 左边右边都找到了
    if(left != null && right != null) {
        return root;
    }
    // 左边找到了，右边没找到
    if(left != null) {
        return left;
    }
    if(right != null) {
        return right;
    }
    return null;
}

Idee 2: Angenommen, der Baum wird in der Darstellung des untergeordneten Elternteils ausgedrückt

Jeder Knoten speichert die Adresse seines Vaters Knoten können Sie Schicht für Schicht online durchsuchen, bis Sie den ersten Schnittpunkt der beiden verknüpften Listen finden, der ihr gemeinsamer Vorfahre ist.

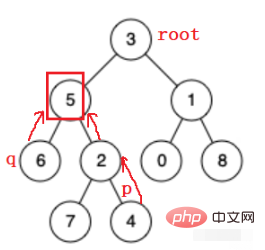Bei gewöhnlichen Binärbäumen können Sie nur Schicht für Schicht nach unten suchen, nicht nach oben, sodass Sie die Pfade der beiden Knoten bis zum letzten identischen Knoten der beiden Pfade beibehalten müssen. Hier verwenden wir einen Stapel, um die Pfade zweier Knoten beizubehalten.

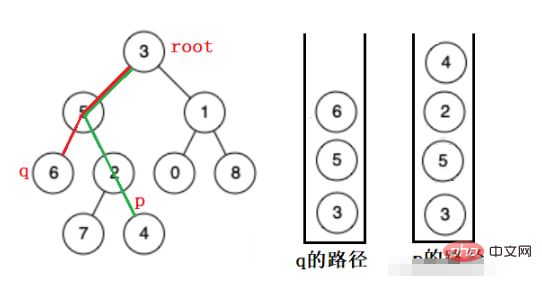Fügen Sie zuerst die Elemente im Stapel hinzu, um weitere Elemente hinzuzufügen, und fügen Sie dann die beiden Stapel zusammen, bis die Knoten, die entfernt werden sollen, gleich sind, was ihr nächster gemeinsamer Vorfahre ist.

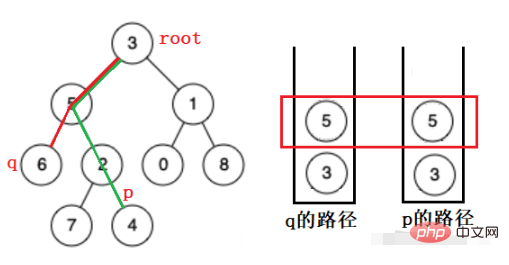Dann ist hier die größte Schwierigkeit der Lagerweg.

Ein Stapel wird hier zum Speichern des Pfads verwendet. Wenn ein Knoten durchlaufen wird, wird der Knoten in den Stapel gelegt und dann werden die linken und rechten Bäume des Knotens rekursiv durchsucht. Wenn der Pfad gefunden wird, wird der Pfad beibehalten , und wenn es nicht gefunden wird, wird es gepoppt.

Angenommen, Sie suchen im Bild unten nach p:

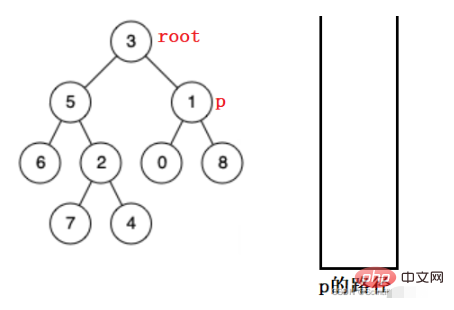Legen Sie zuerst den Wurzelknoten in den Stapel, suchen Sie rekursiv im linken Teilbaum des Wurzelknotens. Wenn er nicht gefunden wird, öffnen Sie ihn und suchen Sie im rechten Teil Teilbaum.

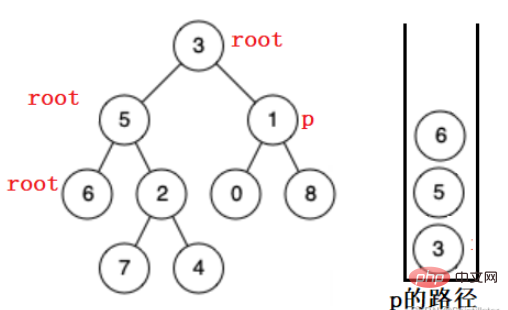Wenn root 6 erreicht, wird festgestellt, dass die linke und rechte Seite des Knotens leer sind, was darauf hinweist, dass der Zielknoten nicht im Teilbaum 6 gefunden wird und die Suche im rechten Teilbaum von 5 fortgesetzt wird .

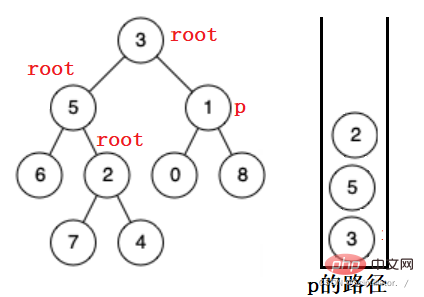Ebenso kann es nicht im richtigen Teilbaum von 5 gefunden werden. Es wird angezeigt, bis es nach dem richtigen Teilbaum von 3 sucht. Wenn es bei 1 ankommt, wird es gefunden.

// 用于找节点的路径
public boolean getPath(TreeNode root, TreeNode node, Stack<TreeNode> stack) {
    if(root == null || node == null) {
        return false;
    }
    // 将当前节点放入栈中
    stack.push(root);
    
    if(root.val == node.val) {
        return true;// 找到了
    }
    // 当前节点没找到，去左子树找
    boolean flag = getPath(root.left,node,stack);
    // 左子树中找到了，直接返回
    if(flag) {
        return true;
    }
    // 左子树没找到，去右子树找
    flag = getPath(root.right,node,stack);
    // 右子树中找到了，直接返回
    if(flag) {
        return true;
    }
    
    // 左右子树都没找到，弹出节点
    stack.pop();
    return false;

}
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    if(root == null) {
        return null;
    }
    Stack<TreeNode> stackp = new Stack<>();
    Stack<TreeNode> stackq = new Stack<>();

    // 分别得到  p q 的路径
    getPath(root,p,stackp);
    getPath(root,q,stackq);

    int sizep = stackp.size();
    int sizeq = stackq.size();

    if(sizep > sizeq) {
        int size = sizep - sizeq;
        // 弹出元素直至两栈中元素个数相等
        while(size > 0) {
            stackp.pop();
            size--;
        }
    }else {
        int size = sizeq - sizep;
        // 弹出元素直至两栈中元素个数相等
        while(size > 0) {
            stackq.pop();
            size--;
        }
    }

    // 一起弹出，直到找到第一个相同的元素
    while(!stackp.isEmpty() && !stackq.isEmpty()) {
        if(stackp.peek() == stackq.peek()) {
        	// 找到了，就返回该节点
            return stackq.pop();
        }else {
            stackp.pop();
            stackq.pop();
        }
    }
    // 没找到，返回 null
    return null;
}

Das obige ist der detaillierte Inhalt vonSo finden Sie den nächsten gemeinsamen Vorfahren eines Binärbaums in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!