Welche Methoden gibt es zur Implementierung magischer Funktionen und Quantencomputersimulation in Python?

Hintergrund der Quantencomputer-Simulation

ProjectQ ist ein sehr elegantes Open-Source-Programmiergerüst für Quantencomputer. Seine ursprünglichen Autoren sind Dr. Damian und Thomas von der Eidgenössischen Technischen Hochschule. Dieses Quantencomputer-Programmierframework ist ein sehr umfassendes Quantencomputer-Programmierframework, das aus Quantencomputeranwendungen –>Quantenschaltungskompilierung –>Hamiltonsche Simulation –>Quantencomputersimulation –>Quantenhardware-API-Docking – implementiert wird. Unterstützt die Installation mit pip: python3 -m pip install projectq --upgrade.

Sehen wir uns ein Beispiel für die Verwendung von projectq zur Simulation von Quantencomputern an:

[dechin@dechin-manjaro simulator]$ ipython
Python 3.8.5 (default, Sep  4 2020, 07:30:14) 
Type 'copyright', 'credits' or 'license' for more information
IPython 7.19.0 -- An enhanced Interactive Python. Type '?' for help.
 
In [1]: from projectq import MainEngine
 
In [2]: from projectq.ops import X
 
In [3]: eng = MainEngine()
 
In [4]: qubits = eng.allocate_qureg(2)
 
In [5]: X | qubits[0]
 
In [6]: from projectq.ops import CX
 
In [7]: CX | (qubits[0], qubits[1])
 
In [8]: eng.flush()
 
In [9]: print (eng.backend.cheat()[1])
[0j, 0j, 0j, (1+0j)]

In diesem Fall haben wir insgesamt 2 Qubits zugewiesen, und die Anfangszustände dieser 2 Bits sind alle |0〉-Zustände, entsprechend The Der von projectq ausgegebene Amplitudenvektor sollte [1, 0, 0, 0] sein. Die vier Elemente in diesem Vektor entsprechen den Wahrscheinlichkeitsamplituden der vier Quantenzustände 00, 01, 10 und 11. Wenn Sie die Wahrscheinlichkeit für die Messung eines bestimmten Zustands berechnen müssen, müssen Sie eine Modulo-Quadrat-Operation daran durchführen :

P(00)=(a₀₀+b₀₀i)(a₀₀−b₀₀i)

Beachten Sie, dass die Wahrscheinlichkeitsamplitude eine komplexe Zahl ist (Komplexe Zahl), Daher muss nach der Konjugation eine Punktmultiplikation durchgeführt werden.

Also zurück zum obigen Anwendungsfall von projectq: In diesem Fall wird nach der Zuweisung von zwei Bits die Pauli-Matrix-Operation σ^X für das erste Bit ausgeführt und anschließend eine Verschränkungs-Gate-Operation CX durchgeführt. Hier sind die der CX(i,j)-Quantengatteroperation entsprechenden Operationen: Wenn sich Qubit i im Zustand |0〉 befindet, wird Qubit i im Zustand |1〉 Inverse Operation, das heißt, wenn das ursprüngliche j |0〉 ist, wird es zu |1〉, wenn das ursprüngliche j |1〉 ist, wird es zu |0〉. Dies ist die Rolle der Quantenverschränkung im Quantencomputing, und die qualitativ hochwertige Implementierung von Multibit-Gate-Operationen in tatsächlichen Hardwaresystemen ist immer noch ein großes Problem. Die Quantenüberlagerungseigenschaft spiegelt sich darin wider, dass sich ein Qubit im |0〉-Zustand befinden kann, oder es kann sich in einem Zwischenzustand zwischen |0〉 befinden wird wie oben erwähnt sein. Um |0〉 und |1〉 b

0

i)P(1)=(a₁+b₁i)⋅(a₁−b

1

i)Diese Wahrscheinlichkeitsamplituden können in organisiert werden Form eines Vektors Aufstehen: |ψ〉=(a₀+b₀i,a

1

+b

1

i)_TAm Ende ist die Anzahl der Die Elemente dieses Vektors nehmen mit der Anzahl der Bits zu. Die Anzahl der Bits nimmt exponentiell zu. Wenn die Anzahl der Bits auf 41 ansteigt, benötigt der für die Speicherung erforderliche Speicherplatz mehr als 32 TB! Es ist zu beachten, dass alle Wahrscheinlichkeitsamplituden während des Berechnungsprozesses in den Speicher geladen werden müssen, was sich vom Festplattenspeicher unterscheidet. Der Speicher allein muss 32 TB groß sein! Daher ist die Verwendung klassischer Computer zur Simulation von Quantencomputern tatsächlich eine sehr ressourcenintensive Methode. Natürlich haben Quantencomputersimulatoren immer noch ihren Forschungswert. In diesem Stadium, in dem Größe und Qualität von Quantenchips nicht verbessert werden können, spielen Simulatoren eine wichtige Rolle. Implementierung der magischen Funktion von PythonWenn Leser einen detaillierten und umfassenden Implementierungsplan für die magische Funktion von Python benötigen, können sie über die Referenzlinks dieses Artikels zwei gute Artikel erhalten. Hier konzentrieren wir uns nur auf einige der Funktionen, die im obigen Anwendungsfall für projectq-Code verwendet werden können: __or__ und __str__, und wir können eine einfache Reproduktion davon erstellen. Mit der magischen Funktion von Python können spezielle Operatoren für eine Klasse definiert werden, z. B. Addition, Subtraktion, Multiplikation und Division der Klasse. Nach Einführung der magischen Funktion besteht keine Notwendigkeit, die Elemente in der Klasse separat zu bedienen. Es können aber auch Magic-Funktionen verwendet werden, um Operationen zu kapseln. Der Endeffekt besteht darin, dass wir Operatoren direkt im Code verwenden können, um verschiedene Klassen zu bearbeiten. Beispielsweise können wir binäre Operatoren wie Klasse1 + Klasse2 anpassen. Wir werden es in diesem Kapitel nicht im Detail vorstellen. Sie können sich auf die spezifischen Anwendungsbeispiele unten oder den Blog-Beitrag im Link beziehen.

Quantenzustandsdefinition und -implementierung

Gemäß der Einführung in Quantenzustandsvektoren im ersten Kapitel können wir hier eine einfache Quantenzustandsklasse implementieren. Wir können nur ein einfaches System aus zwei Qubits betrachten:

# QubitPair.py
import numpy as np
 
class QubitPair:
    def __init__(self):
        self.state = np.array([1, 0, 0, 0], dtype=complex)
 
    def __str__(self):
        return str(self.state)

Dies Die Definition von Eine Quantenzustandsklasse ist sehr einfach, sie ist eine 4×1-Matrix. Es sollte hinzugefügt werden, dass wir hier eine magische Funktion von __str__(self) definieren, die hauptsächlich zum Drucken der String-Darstellung der Klasse verwendet wird. Hier konvertieren wir beispielsweise den Quantenzustandsvektor direkt in das str-Format und geben ihn dann aus. Wenn wir dann eine benutzerdefinierte QubitPair-Klasse drucken, wird die Zeichenfolgendarstellung der Wahrscheinlichkeitsamplitude angezeigt, die der aktuellen Klasse entspricht.

Definition und Implementierung der Quanten-Gate-Operation

Die Quanten-Gate-Operation können wir als eine Matrix betrachten, die auf den Quantenzustandsvektor wirkt. Hier können wir zunächst die Python-Klasse der definierten Gate-Operation zeigen und sie dann erweitern:

# Operator.py
import numpy as np
 
class QubitOperator:
    """Pauli rotations and entanglement on qubit-pair"""
    def __init__(self, operation=None, theta=0, index=0):
        self.index = index
        self.name = operation
        paulix = np.array([[0, 1], [1, 0]], dtype=complex)
        pauliy = np.array([[0, -1j], [1j, 0]], dtype=complex)
        pauliz = np.array([[1, 0], [0, -1]], dtype=complex)
        cnot = np.array([[1, 0, 0, 0],
                         [0, 1, 0, 0],
                         [0, 0, 0, 1],
                         [0, 0, 1, 0]])
        if operation == 'X' or operation == 'Rx':
            self.operation = np.cos(theta/2)*np.identity(2)-1j*np.sin(theta/2)*paulix
        elif operation == 'Y' or operation == 'Ry':
            self.operation = np.cos(theta/2)*np.identity(2)-1j*np.sin(theta/2)*pauliy
        elif operation == 'Z' or operation == 'Rz':
            self.operation = np.cos(theta/2)*np.identity(2)-1j*np.sin(theta/2)*pauliz
        elif operation == 'CX' or operation == 'CNOT':
            self.operation = cnot
 
    def __or__(self, qubitpair):
        if self.name == 'CX' or self.name == 'CNOT':
            qubitpair.state = np.dot(self.operation, qubitpair.state)
            return None
        elif self.index == 0:
            operation = np.kron(self.operation, np.identity(2))
        else:
            operation = np.kron(np.identity(2), self.operation)
        qubitpair.state = np.dot(operation, qubitpair.state)

Definition von Identitätsmatrix und Pauli-Matrix

这些是基本的泡利矩阵，这三个两能级体系的泡利矩阵具有非常好的物理性质，如都是酉矩阵且存在特殊的对易关系等：

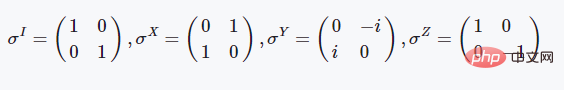
矩阵指数与旋转门操作

矩阵的指数计算一般采用泰勒级数展开的方法来进行定义：

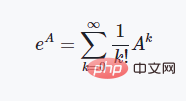
这里如果我们代入上述介绍的泡利矩阵就会得到这样的结果：

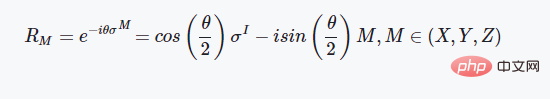
CX门操作的定义

在上述提到的所有的量子门操作中，CX是唯一的一个两比特量子门操作，也就是同时作用在两个量子比特上面，其矩阵形式的定义如下所示：

使用魔法函数__or__来实现量子门操作运算

我们首先简单谈一下为什么要用__or__这个魔法函数而不是其他的二元运算符来实现，这点跟开源库ProjectQ是同步的，理由是我们在量子力学中的运算，一般写成如下的形式：

|ψt〉=U|ψ0〉

将量子态写成狄拉克符号的形式，中文称为"左矢"和"右矢"，英文称之为"bra"和"ket"。因此竖线形式的定义，在形式上会更加契合量子力学的思维，当然，就算是换成其他的符号也是无可厚非的。

功能测试验证

在定义了量子态的类和量子门操作的类之后，我们可以写如下所示的一个测试脚本来测试程序的执行效果：

# TestQubits.py
from QubitPair import QubitPair
from Operator import QubitOperator
 
if __name__ == '__main__':
    qubits = QubitPair()
    print ('The initial state is: {}'.format(qubits))
    QubitOperator('X', 3.1415926, 0) | qubits
    print ('Applying X on the 0th qubit...')
    print ('The new state is: {}'.format(qubits))
    QubitOperator('CX') | qubits
    print ('Applying entanglement on qubits...')
    print ('The new state is: {}'.format(qubits))
    QubitOperator('X', 3.1415926, 0) | qubits
    print ('Applying X on the 0th qubit...')
    print ('The new state is: {}'.format(qubits))
    QubitOperator('CX') | qubits
    print ('Applying entanglement on qubits...')
    print ('The new state is: {}'.format(qubits))

这个程序的测试逻辑为：先定义一个两比特的量子系统，然后对第一个比特执行X门操作，使得其从|0〉态变成|1〉态，再对这两个比特执行纠缠门CX操作，观察其态的变化情况。之后再将第一个比特的状态变回|0〉态，再观察作用CX的态的变化情况，执行结果如下所示：

[dechin@dechin-manjaro simulator]$ python3 TestQubits.py 
The initial state is: [1.+0.j 0.+0.j 0.+0.j 0.+0.j]
Applying X on the 0th qubit...
The new state is: [2.67948966e-08+0.j 0.00000000e+00+0.j 0.00000000e+00-1.j
 0.00000000e+00+0.j]
Applying entanglement on qubits...
The new state is: [2.67948966e-08+0.j 0.00000000e+00+0.j 0.00000000e+00+0.j
 0.00000000e+00-1.j]
Applying X on the 0th qubit...
The new state is: [ 7.17966483e-16+0.00000000e+00j -1.00000000e+00+0.00000000e+00j
  0.00000000e+00-2.67948966e-08j  0.00000000e+00-2.67948966e-08j]
Applying entanglement on qubits...
The new state is: [ 7.17966483e-16+0.00000000e+00j -1.00000000e+00+0.00000000e+00j
  0.00000000e+00-2.67948966e-08j  0.00000000e+00-2.67948966e-08j]

这个结果所展示出来的数字也许比较乱，这是因为在运算过程中的计算精度不足所导致的，这里低于1e-06的数字其实我们可以认为就是0。那么我们从这个结果中可以分析总结出量子态的演变历程：

|00〉⇒|10〉⇒|11〉⇒|01〉⇒|01〉

注意：上面的这种写法，其实不太合乎程序语言的逻辑，一般从右到左的方向才是从低位到高位的写法。因此，严格来说写法应该是：|00〉⇒|01〉⇒|11〉⇒|10〉⇒|10〉。

这里我们就完成了基于魔法函数的量子计算模拟的过程，感兴趣的读者可以自行尝试更多的玩法，这里就不进行更多的测试了！

Das obige ist der detaillierte Inhalt vonWelche Methoden gibt es zur Implementierung magischer Funktionen und Quantencomputersimulation in Python?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!