Python implementiert acht Wahrscheinlichkeitsverteilungsformeln und Tutorials zur Datenvisualisierung

Wahrscheinlichkeit und statistisches Wissen sind der Kern der Datenwissenschaft und des maschinellen Lernens; wir benötigen Statistiken und Wahrscheinlichkeitswissen, um Daten effektiv zu sammeln, zu überprüfen und zu analysieren.

Es gibt mehrere Fälle von Phänomenen in der realen Welt, die als statistischer Natur gelten (z. B. Wetterdaten, Verkaufsdaten, Finanzdaten usw.). Das bedeutet, dass wir in einigen Fällen Methoden entwickeln konnten, die uns helfen, die Natur durch mathematische Funktionen zu simulieren, die die Eigenschaften der Daten beschreiben können. „Eine Wahrscheinlichkeitsverteilung ist eine mathematische Funktion, die die Wahrscheinlichkeit des Auftretens verschiedener möglicher Ergebnisse in einem Experiment angibt.“ Das Verständnis der Datenverteilung hilft, die Welt um uns herum besser zu modellieren. Es kann uns helfen, die Wahrscheinlichkeit verschiedener Ergebnisse zu bestimmen oder die Variabilität von Ereignissen abzuschätzen. All dies macht das Verständnis verschiedener Wahrscheinlichkeitsverteilungen für die Datenwissenschaft und das maschinelle Lernen sehr wertvoll. Gleichmäßige VerteilungDie direkteste Verteilung ist die Gleichverteilung. Eine Gleichverteilung ist eine Wahrscheinlichkeitsverteilung, bei der alle Ergebnisse gleich wahrscheinlich sind. Wenn wir beispielsweise einen fairen Würfel werfen, beträgt die Wahrscheinlichkeit, auf einer beliebigen Zahl zu landen, 1/6. Dies ist eine diskrete Gleichverteilung. Aber nicht alle Gleichverteilungen sind diskret – sie können auch stetig sein. Sie können jeden realen Wert innerhalb des angegebenen Bereichs annehmen. Die Wahrscheinlichkeitsdichtefunktion (PDF) einer kontinuierlichen Gleichverteilung zwischen a und b lautet wie folgt: Sehen wir uns an, wie man sie in Python codiert:

import numpy as np
import matplotlib.pyplot as plt 
from scipy import stats 
 
# for continuous
a = 0 
b = 50 
size = 5000 
 
X_continuous = np.linspace(a, b, size) 
continuous_uniform = stats.uniform(loc=a, scale=b) 
continuous_uniform_pdf = continuous_uniform.pdf(X_continuous) 
 
# for discrete 
X_discrete = np.arange(1, 7) 
discrete_uniform = stats.randint(1, 7) 
discrete_uniform_pmf = discrete_uniform.pmf(X_discrete)
 
# plot both tables 
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(15,5)) 
# discrete plot 
ax[0].bar(X_discrete, discrete_uniform_pmf) 
ax[0].set_xlabel("X") 
ax[0].set_ylabel("Probability") 
ax[0].set_title("Discrete Uniform Distribution") 
# continuous plot 
ax[1].plot(X_continuous, continuous_uniform_pdf) 
ax[1].set_xlabel("X") 
ax[1].set_ylabel("Probability") 
ax[1].set_title("Continuous Uniform Distribution") 
plt.show()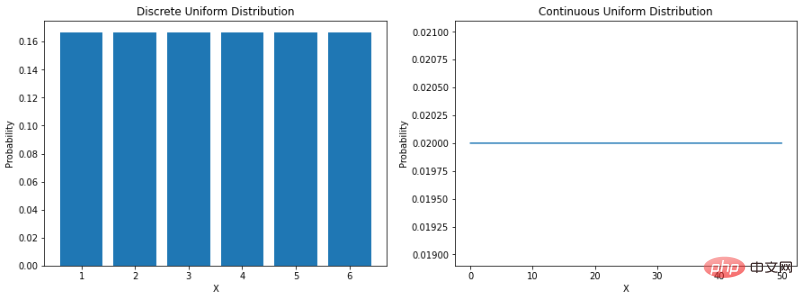

#🎜🎜 # Gaußsche Verteilung

Die Gaußsche Verteilung ist wahrscheinlich die am häufigsten gehörte und bekannteste Verteilung. Sie hat mehrere Namen: Manche nennen sie Glockenkurve, weil ihr Wahrscheinlichkeitsdiagramm wie eine Glocke aussieht, andere nennen sie Gaußsche Verteilung, weil der deutsche Mathematiker Karl Gauß, der sie als Erster beschrieb, sie benannt hat, und wieder andere nennen sie Normalverteilung, weil frühe Statistiker sie bemerkt haben passiert immer und immer wieder. Die Wahrscheinlichkeitsdichtefunktion einer Normalverteilung lautet wie folgt: σ ist die Standardabweichung und μ ist der Mittelwert der Verteilung. Beachten Sie, dass bei einer Normalverteilung der Mittelwert, der Modus und der Median alle gleich sind. Wenn wir eine normalverteilte Zufallsvariable zeichnen, ist die Kurve symmetrisch zum Mittelwert – die Hälfte der Werte liegt links von der Mitte und die andere Hälfte rechts von der Mitte. Und die Gesamtfläche unter der Kurve beträgt 1.

mu = 0 
variance = 1 
sigma = np.sqrt(variance) 
x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100) 
 
plt.subplots(figsize=(8, 5)) 
plt.plot(x, stats.norm.pdf(x, mu, sigma)) 
plt.title("Normal Distribution") 
plt.show()

Für die Normalverteilung. Die Faustregel sagt uns, wie viel Prozent der Daten innerhalb einer bestimmten Anzahl von Standardabweichungen vom Mittelwert liegen. Diese Prozentsätze sind:

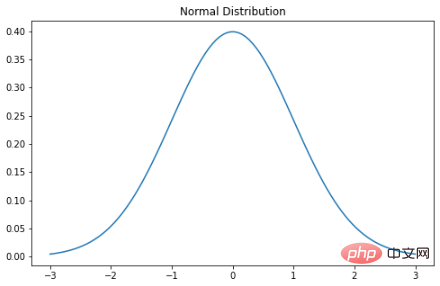
68 % der Daten liegen innerhalb einer Standardabweichung vom Mittelwert.
• 95 % der Daten liegen innerhalb von zwei Standardabweichungen vom Mittelwert.
• 99,7 % der Daten liegen innerhalb von drei Standardabweichungen vom Mittelwert.
• ​

Lognormalverteilung

Die Lognormalverteilung ist der Logarithmus Eine kontinuierliche Wahrscheinlichkeitsverteilung von eine normalverteilte Zufallsvariable. Wenn also die Zufallsvariable X logarithmisch normalverteilt ist, dann ist Y = ln(X) normalverteilt. Hier ist das PDF der Lognormalverteilung: Eine logarithmisch normalverteilte Zufallsvariable nimmt nur positive reelle Werte an. Daher erzeugt die Lognormalverteilung eine rechtsschiefe Kurve. Zeichnen wir es in Python:

X = np.linspace(0, 6, 500) 
 
std = 1 
mean = 0 
lognorm_distribution = stats.lognorm([std], loc=mean) 
lognorm_distribution_pdf = lognorm_distribution.pdf(X) 
 
fig, ax = plt.subplots(figsize=(8, 5)) 
plt.plot(X, lognorm_distribution_pdf, label="μ=0, σ=1") 
ax.set_xticks(np.arange(min(X), max(X))) 
 
std = 0.5 
mean = 0 
lognorm_distribution = stats.lognorm([std], loc=mean) 
lognorm_distribution_pdf = lognorm_distribution.pdf(X) 
plt.plot(X, lognorm_distribution_pdf, label="μ=0, σ=0.5") 
 
std = 1.5 
mean = 1 
lognorm_distribution = stats.lognorm([std], loc=mean) 
lognorm_distribution_pdf = lognorm_distribution.pdf(X) 
plt.plot(X, lognorm_distribution_pdf, label="μ=1, σ=1.5") 
 
plt.title("Lognormal Distribution") 
plt.legend() 
plt.show()

Poisson-Verteilung

Die Poisson-Verteilung ist nach dem französischen Mathematiker Simon Denis benannt. Benannt nach Poisson. Dies ist eine diskrete Wahrscheinlichkeitsverteilung, das heißt, sie zählt Ereignisse mit endlichen Ergebnissen – mit anderen Worten, es handelt sich um eine Zählverteilung. Daher wird die Poisson-Verteilung verwendet, um anzuzeigen, wie oft ein Ereignis innerhalb eines bestimmten Zeitraums auftreten kann. Wenn ein Ereignis mit einer festen zeitlichen Rate auftritt, kann die Wahrscheinlichkeit, die Anzahl (n) der zeitlichen Ereignisse zu beobachten, durch eine Poisson-Verteilung beschrieben werden. Kunden kommen beispielsweise durchschnittlich dreimal pro Minute in ein Café. Mit der Poisson-Verteilung können wir die Wahrscheinlichkeit berechnen, dass 9 Kunden innerhalb von 2 Minuten ankommen. Hier ist die Formel der Wahrscheinlichkeitsmassenfunktion: λ ist die Ereignisrate in einer Zeiteinheit – in unserem Beispiel beträgt sie 3. k ist die Anzahl der Vorkommen – in unserem Fall sind es 9. Hier kann Scipy verwendet werden, um die Wahrscheinlichkeitsberechnung abzuschließen.

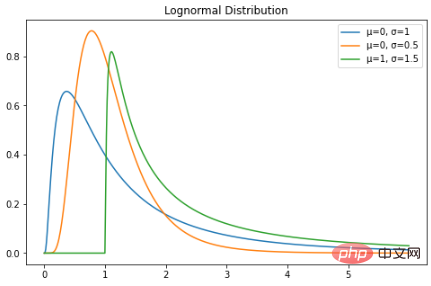
from scipy import stats 

print(stats.poisson.pmf(k=9, mu=3))

0.002700503931560479

Die Kurve der Poisson-Verteilung ähnelt der Normalverteilung und λ stellt den Spitzenwert dar.

X = stats.poisson.rvs(mu=3, size=500) 
 
plt.subplots(figsize=(8, 5)) 
plt.hist(X, density=True, edgecolor="black") 
plt.title("Poisson Distribution") 
plt.show()

Exponentielle Verteilung

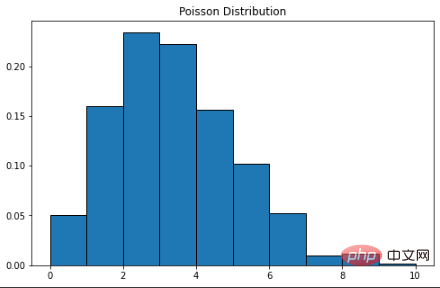
指数分布是泊松点过程中事件之间时间的概率分布。指数分布的概率密度函数如下：λ 是速率参数，x 是随机变量。

X = np.linspace(0, 5, 5000) 
 
exponetial_distribtuion = stats.expon.pdf(X, loc=0, scale=1) 
 
plt.subplots(figsize=(8,5)) 
plt.plot(X, exponetial_distribtuion) 
plt.title("Exponential Distribution") 
plt.show()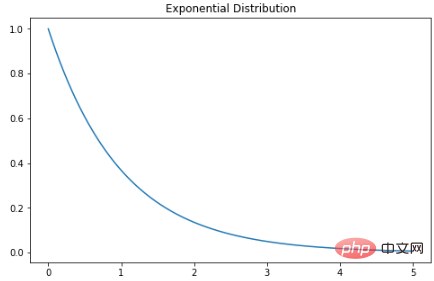

二项分布

可以将二项分布视为实验中成功或失败的概率。有些人也可能将其描述为抛硬币概率。参数为 n 和 p 的二项式分布是在 n 个独立实验序列中成功次数的离散概率分布，每个实验都问一个是 - 否问题，每个实验都有自己的布尔值结果：成功或失败。本质上，二项分布测量两个事件的概率。一个事件发生的概率为 p，另一事件发生的概率为 1-p。这是二项分布的公式：

• P = 二项分布概率
• = 组合数
• x = n次试验中特定结果的次数
• p = 单次实验中，成功的概率
• q = 单次实验中，失败的概率
• n = 实验的次数

可视化代码如下：

X = np.random.binomial(n=1, p=0.5, size=1000) 
 
plt.subplots(figsize=(8, 5)) 
plt.hist(X) 
plt.title("Binomial Distribution") 
plt.show()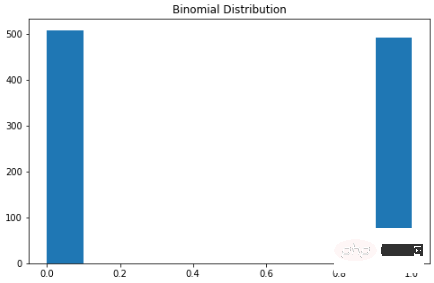

学生 t 分布

学生 t 分布（或简称 t 分布）是在样本量较小且总体标准差未知的情况下估计正态分布总体的均值时出现的连续概率分布族的任何成员。它是由英国统计学家威廉·西利·戈塞特（William Sealy Gosset）以笔名“student”开发的。PDF如下：n 是称为“自由度”的参数，有时可以看到它被称为“d.o.f.” 对于较高的 n 值，t 分布更接近正态分布。

import seaborn as sns 
from scipy import stats 
 
X1 = stats.t.rvs(df=1, size=4) 
X2 = stats.t.rvs(df=3, size=4) 
X3 = stats.t.rvs(df=9, size=4) 
 
plt.subplots(figsize=(8,5)) 
sns.kdeplot(X1, label = "1 d.o.f") 
sns.kdeplot(X2, label = "3 d.o.f") 
sns.kdeplot(X3, label = "6 d.o.f") 
plt.title("Student's t distribution") 
plt.legend() 
plt.show()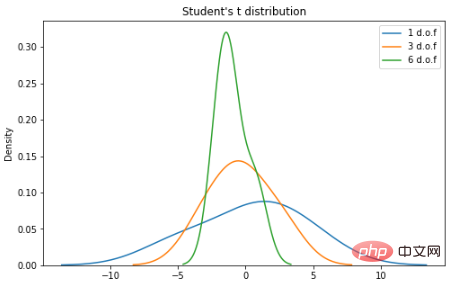

卡方分布

卡方分布是伽马分布的一个特例；对于 k 个自由度，卡方分布是一些独立的标准正态随机变量的 k 的平方和。PDF如下：这是一种流行的概率分布，常用于假设检验和置信区间的构建。在 Python 中绘制一些示例图：

X = np.arange(0, 6, 0.25) 
 
plt.subplots(figsize=(8, 5)) 
plt.plot(X, stats.chi2.pdf(X, df=1), label="1 d.o.f") 
plt.plot(X, stats.chi2.pdf(X, df=2), label="2 d.o.f") 
plt.plot(X, stats.chi2.pdf(X, df=3), label="3 d.o.f") 
plt.title("Chi-squared Distribution") 
plt.legend() 
plt.show()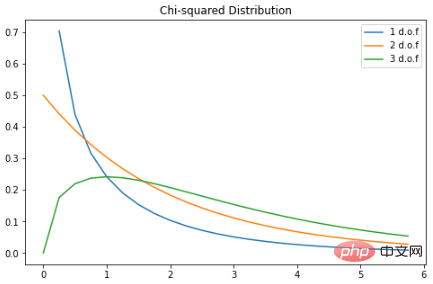

掌握统计学和概率对于数据科学至关重要。在本文展示了一些常见且常用的分布，希望对你有所帮助。

Das obige ist der detaillierte Inhalt vonPython implementiert acht Wahrscheinlichkeitsverteilungsformeln und Tutorials zur Datenvisualisierung. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!