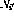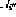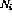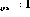Heim >Technologie-Peripheriegeräte >KI >Ist die Turing-Maschine das heißeste wiederkehrende neuronale Netzwerk RNN im Deep Learning? Die Arbeit von 1996 hat es bewiesen!
Ist die Turing-Maschine das heißeste wiederkehrende neuronale Netzwerk RNN im Deep Learning? Die Arbeit von 1996 hat es bewiesen!
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2023-04-25 21:25:06901Durchsuche
Vom 19. bis 23. August 1996 fand in Vaasa, Finnland, die finnische Konferenz für künstliche Intelligenz statt, die von der finnischen Vereinigung für künstliche Intelligenz und der Universität Vaasa organisiert wurde.
Ein auf der Konferenz veröffentlichtes Papier bewies, dass die Turing-Maschine ein wiederkehrendes neuronales Netzwerk ist.
Ja, das ist 26 Jahre her!
Werfen wir einen Blick auf dieses 1996 veröffentlichte Papier.
1 Einführung
1.1 Klassifizierung neuronaler Netze
Neuronale Netze können für Klassifizierungsaufgaben verwendet werden, um festzustellen, ob das Eingabemuster zu einer bestimmten Kategorie gehört.
Es ist seit langem bekannt, dass einschichtige Feedforward-Netzwerke nur zur Klassifizierung linear trennbarer Muster verwendet werden können, d. h. je mehr aufeinanderfolgende Schichten, desto komplexer die Klassenverteilung.
Wenn Feedback in die Netzwerkstruktur eingeführt wird, wird der Perzeptron-Ausgabewert recycelt und die Anzahl aufeinanderfolgender Schichten wird im Prinzip unendlich.
Wurde die Rechenleistung qualitativ verbessert? Die Antwort ist ja.
Zum Beispiel kann ein Klassifikator erstellt werden, um zu bestimmen, ob die eingegebene Ganzzahl eine Primzahl ist.
Es stellt sich heraus, dass die Größe des für diesen Zweck verwendeten Netzwerks endlich sein kann, und selbst wenn die Größe der eingegebenen Ganzzahl nicht begrenzt ist, ist die Anzahl der Primzahlen, die korrekt klassifiziert werden können, unendlich.
In diesem Artikel kann „eine zyklische Netzwerkstruktur, die aus denselben Rechenelementen besteht“ verwendet werden, um jede (algorithmisch) berechenbare Funktion zu vervollständigen.
1.2 Über Berechenbarkeit
Nach den grundlegenden Axiomen der Berechenbarkeitstheorie können berechenbare Funktionen mithilfe von Turing-Maschinen implementiert werden. Es gibt viele Möglichkeiten, Turing-Maschinen zu implementieren.
Programmiersprache definieren . Die Sprache verfügt über vier Grundoperationen:
. Die Sprache verfügt über vier Grundoperationen:

Hier repräsentiert V jede Variable mit einem positiven ganzzahligen Wert und j jede Zeilennummer.
Es kann gezeigt werden, dass eine Funktion, wenn sie Turing-berechenbar ist, mit dieser einfachen Sprache codiert werden kann (siehe [1] für Details).
2 Turing-Netzwerk
2.1 Rekursive neuronale Netzwerkstruktur
Das in diesem Artikel untersuchte neuronale Netzwerk besteht aus Perzeptronen, die alle die gleiche Struktur haben q kann als definiert werden
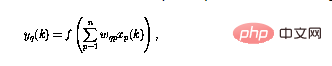
wobei der Perzeptron-Output im aktuellen Moment (gekennzeichnet mit 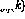 ) unter Verwendung der n-Eingabe
) unter Verwendung der n-Eingabe  berechnet wird.
berechnet wird.
Die nichtlineare Funktion f kann nun als
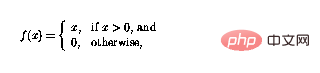
definiert werden. Auf diese Weise kann die Funktion negative Werte einfach „abschneiden“, und Schleifen im Perzeptron-Netzwerk führen dazu, dass Perzeptrone auf komplexe Weise kombiniert werden können .
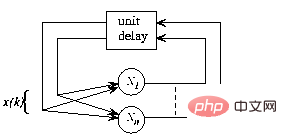
Abbildung 1 Der Gesamtrahmen des rekurrenten neuronalen Netzwerks, die Struktur ist autonom und ohne externe Eingaben und das Netzwerkverhalten wird vollständig durch den Anfangszustand bestimmt
In Abbildung 1 ist die rekursive Struktur in a dargestellt Allgemeiner Rahmen: Nun ist 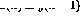 und n die Anzahl der Perzeptrone, und die Verbindung von Perzeptron p zu Perzeptron q wird durch das Skalargewicht
und n die Anzahl der Perzeptrone, und die Verbindung von Perzeptron p zu Perzeptron q wird durch das Skalargewicht 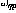 in (1) dargestellt.
in (1) dargestellt.
Das heißt, bei einem gegebenen Anfangszustand iteriert der Netzwerkzustand, bis er sich nicht mehr ändert, und die Ergebnisse können im stabilen Zustand oder am „Fixpunkt“ des Netzwerks gelesen werden.
2.2 Aufbau eines neuronalen Netzwerks
Als nächstes erklären wir, wie dieses Programm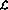 im Perzeptronnetzwerk implementiert wird. Das Netzwerk besteht aus den folgenden Knoten (oder Perzeptronen):
im Perzeptronnetzwerk implementiert wird. Das Netzwerk besteht aus den folgenden Knoten (oder Perzeptronen):
-
Für jede Variable V im Programm gibt es einen Variablenknoten
 .
. -
Für jede Programmzeile i gibt es einen Anweisungsknoten
 .
. -
Für jede bedingte Verzweigungsanweisung in Zeile i gibt es zwei zusätzliche Verzweigungsknoten
 und
und  . Die Implementierung des
. Die Implementierung des
Sprachprogramms 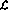 besteht aus den folgenden Änderungen am Perzeptron-Netzwerk:
besteht aus den folgenden Änderungen am Perzeptron-Netzwerk:
- Für jede Änderung V im Programm erweitern Sie das Netzwerk über den folgenden Link:

-
Wenn es in Zeile i des Programmcodes keine Operation (
 ) gibt, dann wird das Netzwerk über den folgenden Link erweitert (vorausgesetzt, dass Knoten
) gibt, dann wird das Netzwerk über den folgenden Link erweitert (vorausgesetzt, dass Knoten  existiert:
existiert:

-
) Wenn In Zeile i gibt es eine inkrementelle Operation (
 ). Erweitern Sie das Netzwerk wie folgt:
). Erweitern Sie das Netzwerk wie folgt:

-
Wenn Zeile i eine Dekrementierungsoperation (
 ) hat, dann erweitern Sie das Netzwerk wie folgt:
) hat, dann erweitern Sie das Netzwerk wie folgt:
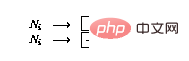
-
Wenn Zeile i eine bedingte Verzweigung (
 ) hat, dann erweitern Sie das Netzwerk wie folgt: Erweiterung des Netzwerks:
) hat, dann erweitern Sie das Netzwerk wie folgt: Erweiterung des Netzwerks:
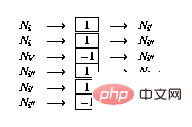
2.3 Äquivalenznachweis
Was nun bewiesen werden muss, ist, dass „der interne Zustand des Netzwerks oder der Inhalt des Netzwerkknotens“ durch den Programmstatus identifiziert werden kann, und die Kontinuität des Netzwerkstatus stimmt mit der Programm-Stream-Korrespondenz überein.
definiert den „Rechtszustand“ des Netzwerks wie folgt:
-
Die Ausgabe an alle Übergangsknoten
 und
und  (wie in 2.2 definiert) ist Null (
(wie in 2.2 definiert) ist Null ( );
);
-
Höchstens ein Befehlsknoten
 hat einen Einheitsausgang (
hat einen Einheitsausgang ( ), alle anderen Befehlsknoten haben einen Nullausgang und
), alle anderen Befehlsknoten haben einen Nullausgang und
- Variablenknoten haben nichtnegative ganzzahlige Ausgangswerte.
Wenn die Ausgaben aller Befehlsknoten Null sind, ist der Zustand Endzustand. Ein gültiger Netzwerkstatus kann direkt als Programm-„Schnappschuss“ interpretiert werden – wenn , befindet sich der Programmzähler in Zeile i und der entsprechende Variablenwert wird im Variablenknoten gespeichert.
Änderungen im Netzwerkstatus werden durch Knoten ungleich Null aktiviert.
Konzentrieren Sie sich zunächst auf die variablen Knoten. Es stellt sich heraus, dass sie sich wie Integratoren verhalten und der vorherige Inhalt des Knotens auf denselben Knoten zurückgeführt wird.
Die einzigen Verbindungen von variablen Knoten zu anderen Knoten haben negative Gewichte – deshalb ändern sich Knoten, die Nullen enthalten, aufgrund der Nichtlinearität nicht (2).
Als nächstes wird der Anweisungsknoten im Detail erklärt. Nehmen Sie an, dass der einzige Befehlsknoten ungleich Null zum Zeitpunkt k liegt – dies entspricht dem Programmzähler in Zeile i im Programmcode.
Wenn die i-Zeile im Programm lautet, kann das Verhalten des Netzwerks, das einen Schritt vorwärts macht, ausgedrückt werden als (nur betroffene Knoten werden angezeigt)
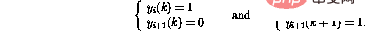
Fakten haben bewiesen, dass der neue Netzwerkstatus wieder legal ist. Im Vergleich zum Programmcode entspricht dies einer Verschiebung des Programmzählers in Zeile i+1.
Wenn andererseits die ite Zeile im Programm 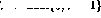 ist, ist das Verhalten eines Schritts vorwärts
ist, ist das Verhalten eines Schritts vorwärts
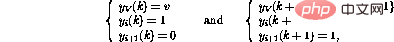
Auf diese Weise wird zusätzlich zum Verschieben des Programmzählers in die nächste Zeile verschoben , die Variable V Der Wert von wird ebenfalls abnehmen. Wenn Linie i
 wäre, wäre der Betrieb des Netzwerks derselbe, außer dass der Wert der Variablen V erhöht wird.
wäre, wäre der Betrieb des Netzwerks derselbe, außer dass der Wert der Variablen V erhöht wird.
Die bedingte Verzweigungsoperation (IF GOTO  j) in Zeile i aktiviert eine komplexere Abfolge von Operationen:
j) in Zeile i aktiviert eine komplexere Abfolge von Operationen:
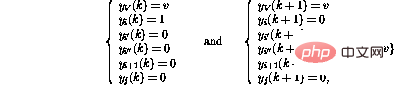
Schließlich
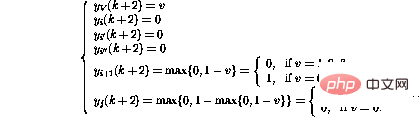
Es stellt sich heraus dass nach diesen Schritten der Netzwerkzustand wieder als ein weiterer Programm-Snapshot interpretiert werden kann.
Der Variablenwert hat sich geändert und der Token wurde an den neuen Speicherort übertragen, so als ob die entsprechende Programmzeile ausgeführt würde.
Wenn das Token verschwindet, ändert sich der Netzwerkstatus nicht mehr – dies kann nur passieren, wenn der Programmzähler den Programmcode „übersteigt“, was bedeutet, dass das Programm beendet wird.
Der Betrieb des Netzwerks ähnelt auch dem Betrieb des entsprechenden Programms und der Beweis ist vollständig.
3 Modifikationen
3.1 Erweiterungen
Es ist einfach, zusätzliche optimierte Anweisungen zu definieren, die das Programmieren einfacher und die resultierenden Programme lesbarer und schneller ausführbar machen. Beispielsweise kann der unbedingte Zweig (GOTO j) in Zeile i
von-
implementiert werden, indem
-
die Konstante c zur Variablen () in Zeile i hinzugefügt wird kann ein weiterer bedingter Zweig (IF V=0 GOTO
j ) online sein. i kann als -
Eine Inkrementierungs-/Dekrementierungsanweisung implementiert werden. Angenommen, Sie möchten Folgendes tun:
. Es wird nur ein Knoten benötigt -
:Die obige Methode ist keineswegs die einzige Möglichkeit, eine Turing-Maschine zu implementieren.
Dies ist eine einfache Implementierung und in Anwendungen möglicherweise nicht unbedingt optimal.
3.2 Matrixformulierung
Die obige Konstruktion kann auch in Form einer Matrix implementiert werden.
Die Grundidee besteht darin, Variablenwerte und „Programmzähler“ in Prozesszuständen s
zu speichern und die ZustandsübergangsmatrixA die Verbindungen zwischen Knoten darstellen zu lassen.
Der Betrieb der Matrixstruktur kann als zeitdiskreter dynamischer Prozess definiert werden wobei die nichtlineare vektorwertige Funktion ZustandsübergangsmatrixA lässt sich leicht aus der Netzwerkformel entschlüsseln – die Matrixelemente sind die Gewichte zwischen Knoten. Diese Matrixformel ähnelt dem in [3] vorgeschlagenen „Konzeptmatrix“-Framework. Angenommen, Sie möchten eine einfache Funktion y=x implementieren, das heißt, der Wert der Eingabevariablen x soll an die Ausgabevariable y übergeben werden. Unter Verwendung der Sprache Das resultierende Perzeptron-Netzwerk ist in Abbildung 2 dargestellt. Die durchgezogene Linie stellt eine positive Verbindung dar (Gewicht 1) und die gepunktete Linie stellt eine negative Verbindung dar (Gewicht -1). Im Vergleich zu Abbildung 1 wird die Netzwerkstruktur durch die Integration von Verzögerungselementen in den Knoten neu gezeichnet und vereinfacht. Abbildung 2: Netzwerkimplementierung eines einfachen Programms Mit Links zu Knoten, die die beiden Variablen und Dann gibt es den Anfangszustand (vor der Iteration) und den Endzustand (nach der Iteration, wenn der Fixpunkt gefunden wird)
Wenn der Wert des variablen Knotens streng zwischen 0 und 1 gehalten wird, dann ist die Operation des dynamischen Systems (3) linear und die Funktion hat überhaupt keine Wirkung. Grundsätzlich kann dann die lineare Systemtheorie in der Analyse eingesetzt werden. A dargestellt. Es stellt sich heraus, dass Iterationen immer nach Schritten konvergieren, wobei . Abbildung 3 „Eigenwert“ eines einfachen Programms Es stellt sich heraus, dass Turingmaschinen als Perzeptronnetzwerke kodiert werden können. Per Definition sind alle berechenbaren Funktionen Turing-berechenbar – im Rahmen der Berechenbarkeitstheorie gibt es kein leistungsfähigeres Rechensystem. Daraus lässt sich schließen: Ein rekurrentes Perzeptronnetzwerk (siehe oben) ist (noch eine weitere) Form einer Turingmaschine. Der Vorteil dieser Äquivalenz besteht darin, dass die Ergebnisse der Berechenbarkeitstheorie leicht zu erhalten sind – beispielsweise ist es bei einem gegebenen Netzwerk und einem Anfangszustand unmöglich zu sagen, ob der Prozess irgendwann zum Stillstand kommt. Die obige theoretische Äquivalenz sagt nichts über die Recheneffizienz aus. Die verschiedenen Mechanismen, die im Netzwerk ablaufen, können dazu führen, dass einige Funktionen in diesem Framework besser implementiert werden als bei herkömmlichen Turing-Maschinen-Implementierungen (bei denen es sich eigentlich um heutige Computer handelt). Zumindest in einigen Fällen kann beispielsweise eine Netzwerkimplementierung eines Algorithmus parallelisiert werden, indem mehrere „Programmzähler“ im Snapshot-Vektor zugelassen werden. Der Betrieb des Netzwerks ist streng lokal und nicht global. Eine interessante Frage stellt sich beispielsweise, ob das NP-vollständige Problem in einer Netzwerkumgebung effizienter angegangen werden kann! Im Vergleich zur Sprache Im Vergleich zum ursprünglichen Programmcode ist die Matrixformel offensichtlich eine „kontinuierlichere“ Informationsdarstellung als der Programmcode – die Parameter können (häufig) geändert werden und die Iterationsergebnisse ändern sich nicht plötzlich. Diese „Redundanz“ kann in einigen Anwendungen nützlich sein. Wenn Sie beispielsweise einen genetischen Algorithmus (GA) zur Strukturoptimierung verwenden, kann die im genetischen Algorithmus verwendete Zufallssuchstrategie effizienter gestaltet werden: Nach Änderungen der Systemstruktur kann das lokale Minimum der kontinuierlichen Kostenfunktion erreicht werden mit traditioneller Technologie durchsucht (siehe [4]). Wenn Sie die Struktur endlicher Zustandsmaschinen anhand von Beispielen lernen, wie in [5] beschrieben, können Sie erkennen, dass die Methode der iterativen Verbesserung der Netzwerkstruktur auch in diesem komplexeren Fall verwendet wird. Nicht nur die Theorie neuronaler Netze kann von den obigen Ergebnissen profitieren – wenn man sich nur die dynamische Systemformel (3) ansieht, ist es offensichtlich, dass alle im Bereich der Berechenbarkeitstheorie vorkommenden Phänomene auch in einfacher Form existieren – auf der Suche nach nichtlinearer Dynamik Verfahren. Zum Beispiel ist die Unentscheidbarkeit des Halteproblems ein interessanter Beitrag zur Systemtheorie: Für jeden Entscheidungsprozess, der als Turingmaschine dargestellt wird, gibt es dynamische Systeme der Form (3), die diesen Prozess verletzen – z.B. Konstrukt ein allgemeiner Stabilitätsanalysealgorithmus. Es gibt einige Ähnlichkeiten zwischen der vorgestellten Netzwerkstruktur und dem rekursiven Hopfield-Neuronalen Netzwerkparadigma (siehe beispielsweise [2]). In beiden Fällen wird die „Eingabe“ als Anfangszustand im Netzwerk kodiert und die „Ausgabe“ wird nach Iterationen aus dem Endzustand des Netzwerks gelesen. Der Fixpunkt des Hopfield-Netzwerks ist ein vorprogrammiertes Mustermodell, und die Eingabe ist ein „Rauschen“-Muster – das Netzwerk kann zur Verbesserung beschädigter Muster verwendet werden. Der Ausblick (2) der nichtlinearen Funktion in Verglichen mit dem Hopfield-Netzwerk, bei dem die Einheitenausgabe immer -1 oder 1 beträgt, ist ersichtlich, dass diese Netzwerkstrukturen theoretisch sehr unterschiedlich sind. Während beispielsweise die Menge stabiler Punkte in einem Hopfield-Netzwerk begrenzt ist, haben Programme, die durch Turing-Netzwerke dargestellt werden, oft eine unbegrenzte Anzahl möglicher Ergebnisse. Die Rechenfähigkeiten von Hopfield-Netzwerken werden in [6] diskutiert. Petri-Netz ist ein leistungsstarkes Werkzeug für die ereignisbasierte und gleichzeitige Systemmodellierung [7]. Ein Petri-Netz besteht aus Bits und Übergängen und den sie verbindenden Bögen. Jeder Ort kann eine beliebige Anzahl von Token enthalten, und die Verteilung der Token wird als Markierung des Petri-Netzes bezeichnet. Wenn alle Eingabepositionen einer Transformation durch Markierungen belegt sind, kann die Transformation ausgelöst werden, indem eine Markierung von jeder Eingabeposition entfernt und an jeder ihrer Ausgabepositionen eine Markierung hinzugefügt wird. Es kann nachgewiesen werden, dass erweiterte Petri-Netze mit zusätzlichen Unterdrückungsbögen auch die Fähigkeiten von Turingmaschinen besitzen (siehe [7]). Der Hauptunterschied zwischen den oben genannten Turing-Netzen und Petri-Netzen besteht darin, dass das Gerüst von Petri-Netzen komplexer ist und eine speziell angepasste Struktur aufweist, die nicht durch eine einfache allgemeine Form ausgedrückt werden kann (3). Referenz 1 Davis, M. und Weyuker, E.: Berechenbarkeit, Komplexität und Sprachen – Grundlagen der Theoretischen Informatik, New York, 1983. 2 Haykin, S.: Eine umfassende Grundlage. Macmillan College Publishing, New York, 1994. 3 Hyötyniemi, H.: Bausteine der Intelligenz? Dimensions of Intelligence), Finnish Artificial Intelligence Society, 1995, S. 199--226. 4 Hyötyniemi, H. und Koivo, H.: Gene, Codes, and Dynamic Systems on Genetic Algorithms (NWGA'96), Vaasa, Finnland, 19.–23. August 1996. 5 Manolios, P. und Fanelli, R.: First-Order Recurrent Neural Networks and Deterministic Finite State Automata 6 , 1994, S. 1155--1173. 6 Orponen, P.: The Computational Power of Discrete Hopfield Nets with Hidden Units. Neural Computation 8, 1996, S. 403--415. 7 Peterson , J.L.: Petri Net Theory and the Modeling of Systems /link/0465a1824942fac19824528343613213 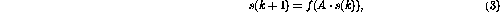
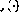 nun elementweise wie in (2) definiert ist. Der Inhalt der
nun elementweise wie in (2) definiert ist. Der Inhalt der 4 Beispiel
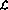 kann dies wie folgt kodiert werden (der „Eintrittspunkt“ sei nun nicht die erste Zeile, sondern die dritte Zeile):
kann dies wie folgt kodiert werden (der „Eintrittspunkt“ sei nun nicht die erste Zeile, sondern die dritte Zeile): 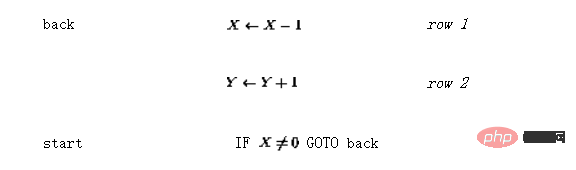
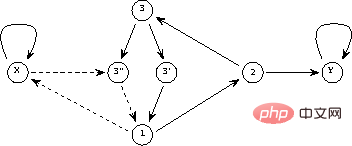 X
X
Selbst wenn es im obigen Beispiel Eigenwerte außerhalb des Einheitskreises gibt, ist die Iteration aufgrund der Nichtlinearität immer stabil. 5 Diskussion
5.1 Theoretische Aspekte
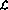 weist die Netzwerkimplementierung die folgenden „Erweiterungen“ auf:
weist die Netzwerkimplementierung die folgenden „Erweiterungen“ auf:
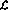 , in der alle dargestellten Zahlen rationale Zahlen sind.
, in der alle dargestellten Zahlen rationale Zahlen sind.
5.2 Verwandte Arbeiten
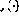 macht die Anzahl der möglichen Zustände im oben genannten „Turing-Netzwerk“ unendlich.
macht die Anzahl der möglichen Zustände im oben genannten „Turing-Netzwerk“ unendlich.
Das obige ist der detaillierte Inhalt vonIst die Turing-Maschine das heißeste wiederkehrende neuronale Netzwerk RNN im Deep Learning? Die Arbeit von 1996 hat es bewiesen!. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Technologietrends, die Sie im Jahr 2023 im Auge behalten sollten
- Wie künstliche Intelligenz Rechenzentrumsteams neue Alltagsaufgaben beschert
- Können künstliche Intelligenz oder Automatisierung das Problem der geringen Energieeffizienz in Gebäuden lösen?
- OpenAI-Mitbegründer im Interview mit Huang Renxun: Die Argumentationsfähigkeiten von GPT-4 haben noch nicht die Erwartungen erfüllt
- Dank der OpenAI-Technologie übertrifft Bing von Microsoft Google im Suchverkehr


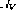 .
. 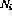 .
. 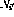 und
und 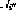 . Die Implementierung des
. Die Implementierung des 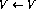 ) gibt, dann wird das Netzwerk über den folgenden Link erweitert (vorausgesetzt, dass Knoten
) gibt, dann wird das Netzwerk über den folgenden Link erweitert (vorausgesetzt, dass Knoten 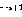 existiert:
existiert:  ). Erweitern Sie das Netzwerk wie folgt:
). Erweitern Sie das Netzwerk wie folgt:  ) hat, dann erweitern Sie das Netzwerk wie folgt:
) hat, dann erweitern Sie das Netzwerk wie folgt:  ) hat, dann erweitern Sie das Netzwerk wie folgt: Erweiterung des Netzwerks:
) hat, dann erweitern Sie das Netzwerk wie folgt: Erweiterung des Netzwerks: