Vergleichen Sie Zeitreihenvorhersagemethoden basierend auf SARIMA, XGBoost und CNN-LSTM.

Verwendung statistischer Tests und maschinellen Lernens zur Analyse und Vorhersage von Leistungstests und -vergleichen bei der Solarstromerzeugung.

In diesem Artikel werden Techniken zur Erzielung greifbarer Werte aus Datensätzen mithilfe von Hypothesentests, Feature-Engineering, Zeitreihenmodellierungsmethoden und mehr erörtert. Ich werde mich auch mit Themen wie Datenlecks und Datenaufbereitung für verschiedene Zeitreihenmodelle befassen und Vergleichstests von drei gängigen Zeitreihenprognosen durchführen.

Einführung

Zeitreihenvorhersage ist ein häufig untersuchtes Thema. Hier verwenden wir die Daten von zwei Solarkraftwerken, um deren Gesetze zu untersuchen und Modellierungen durchzuführen. Gehen Sie diese Probleme an, indem Sie sie zunächst in zwei Fragen zusammenfassen:

1. Ist es möglich, leistungsschwache Solarmodule zu identifizieren?
2. Ist es möglich, die Solarstromerzeugung für zwei Tage vorherzusagen?

Bevor wir mit der Beantwortung dieser Fragen fortfahren, wollen wir zunächst verstehen, wie Solarkraftwerke Strom erzeugen.

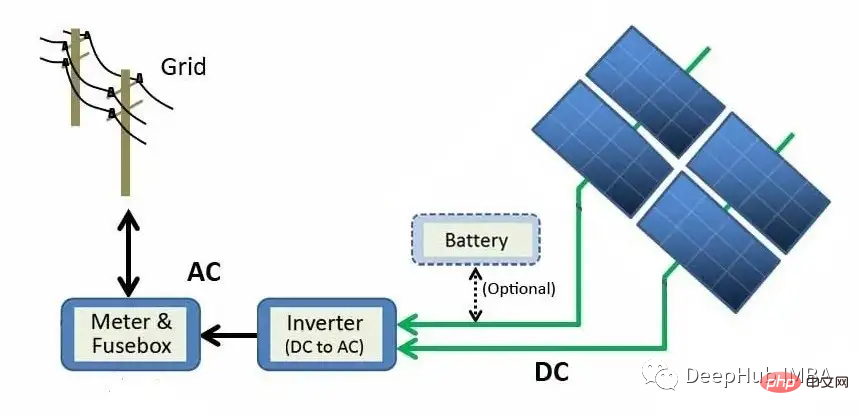
Das obige Diagramm beschreibt den Erzeugungsprozess von Solarmodulen bis zum Netz. Durch den photoelektrischen Effekt wird Sonnenenergie direkt in elektrische Energie umgewandelt. Wenn Materialien wie Silizium (das häufigste Halbleitermaterial in Solarpaneelen) Licht ausgesetzt werden, werden Photonen (subatomare Teilchen elektromagnetischer Energie) absorbiert und freie Elektronen freigesetzt, wodurch Gleichstrom (DC) entsteht. Mithilfe eines Wechselrichters wird Gleichstrom in Wechselstrom (AC) umgewandelt und ins Netz eingespeist, wo er an Haushalte verteilt werden kann.

Daten

Die Rohdaten bestehen aus zwei durch Kommas getrennten Wertdateien (CSV) für jedes Solarkraftwerk. Ein Dokument zeigt den Stromerzeugungsprozess und das andere die von den Sensoren des Solarparks aufgezeichneten Messungen. Die beiden Datensätze für jedes Solarkraftwerk wurden in einem Pandas-DF organisiert.

Daten von Solarkraftwerk 1 (SP1) und Solarkraftwerk 2 (SP2) wurden vom 15. Mai 2020 bis 18. Juni 2020 alle 15 Minuten erfasst. Sowohl SP1- als auch SP2-Datensätze enthalten dieselben Variablen.

• Datum Uhrzeit – ein Intervall von 15 Minuten
• Umgebungstemperatur – die Temperatur der Luft um das Modul herum
• Modultemperatur – die Temperatur des Moduls
• Bestrahlung – die Strahlung auf dem Modul
• DC-Leistung (kW) - DC
• AC Leistung (kW) - AC
• Tagesertrag – Gesamte tägliche Stromerzeugung
• Gesamtertrag – Kumulierte Leistung des Wechselrichters
• Anlagen-ID – Eindeutige Identifikation des Solarkraftwerks
• Modul-ID – Eindeutige Identifikation von Jedes Modul

Wettersensoren werden verwendet, um Umgebungstemperatur, Modultemperatur und Strahlung an jeder Solaranlage zu erfassen.

Für diesen Datensatz ist die Gleichstromleistung die abhängige Variable (Zielvariable). Unser Ziel ist es, leistungsschwache Solarmodule zu finden.

Zwei unabhängige DFS für Analyse und Vorhersage. Der einzige Unterschied besteht darin, dass die für die Prognose verwendeten Daten auf stündliche Intervalle umgerechnet werden, während der für die Analyse verwendete Datenrahmen 15-Minuten-Intervalle enthält.

Zuerst entfernen wir die Pflanzen-ID, da sie keinen Mehrwert für den Versuch bietet, die obige Frage zu beantworten. Modul-IDs werden ebenfalls aus dem Vorhersagedatensatz entfernt. Die Tabellen 1 und 2 zeigen Datenbeispiele.

Bevor wir die Daten weiter analysierten, haben wir einige Annahmen über das Solarkraftwerk getroffen, darunter:

• Das Datenerfassungsinstrument ist fehlerfrei
• Das Modul wird regelmäßig gereinigt (ohne Berücksichtigung der Auswirkungen von Wartung)
• Zwei Solaranlagen. Es gibt keine Okklusionsprobleme rund um das Kraftwerk

Explorative Datenanalyse (EDA)

Für Neulinge in der Datenwissenschaft ist EDA ein entscheidender Schritt zum Verständnis der Daten durch die Darstellung von Visualisierungen und die Durchführung statistischer Tests. Wir können zunächst die Leistung jedes Solarkraftwerks beobachten, indem wir Gleich- und Wechselstrom für SP1 und SP2 grafisch darstellen.

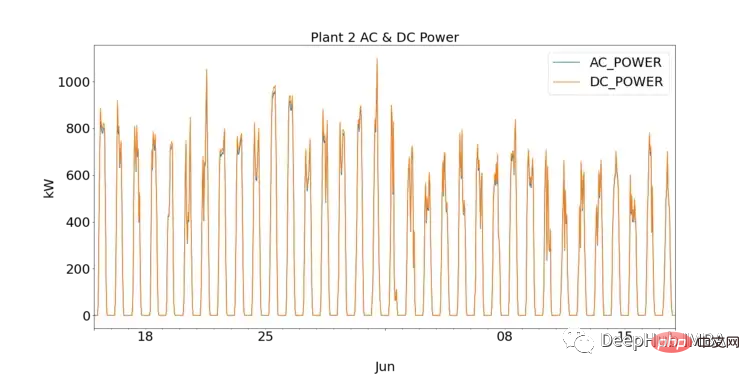
SP1 zeigt eine um eine Größenordnung höhere Gleichstromleistung als sp2. Unter der Annahme, dass die von SP1 gesammelten Daten korrekt sind und das zum Aufzeichnen der Daten verwendete Instrument nicht fehlerhaft ist, deutet dies darauf hin, dass der Wechselrichter in SP1 eingehender untersucht werden muss

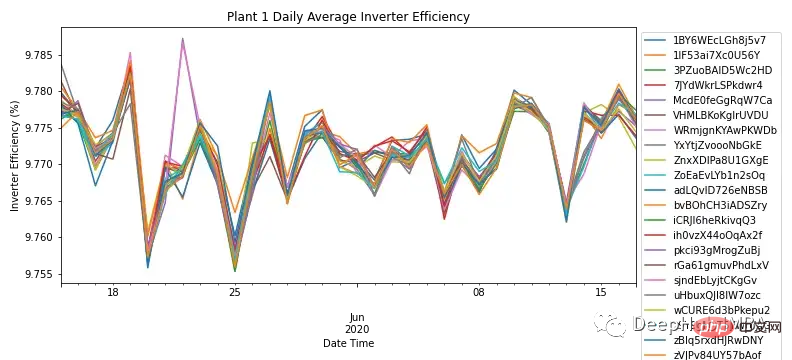
durch Aggregieren von Wechsel- und Gleichstrom durch die tägliche Häufigkeit von Für jedes Modul zeigt Abbildung 3 den Wechselrichterwirkungsgrad aller Module in SP1. Der Wirkungsgrad von Solarwechselrichtern sollte nach Fachkenntnissen zwischen 93 und 96 % liegen. Da der Wirkungsgradbereich für alle Module zwischen 9,76 % und 9,79 % liegt, verdeutlicht dies die Notwendigkeit, die Leistung des Wechselrichters zu untersuchen und festzustellen, ob er ausgetauscht werden muss.

Da bei SP1 Probleme mit dem Wechselrichter auftraten, erfolgte eine weitere Analyse nur zu SP2.

Obwohl diese kurze Analyse das Ergebnis einer längeren Untersuchung des Wechselrichters ist, beantwortet sie nicht die Hauptfrage der Bestimmung der Leistung von Solarmodulen.

Da der Wechselrichter des SP2 ordnungsgemäß funktioniert, können etwaige Anomalien identifiziert und untersucht werden, indem tiefer in die Daten eingetaucht wird.

Abbildung 4 zeigt den Zusammenhang zwischen Modultemperatur und Umgebungstemperatur. Es gibt Fälle, in denen die Modultemperatur extrem hoch ist.

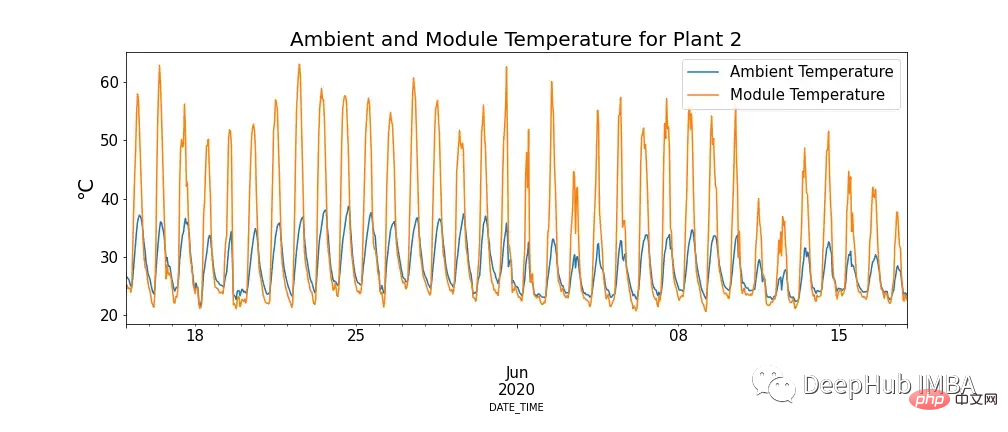
Das scheint zwar unserem Wissen zu widersprechen, aber es zeigt sich, dass hohe Temperaturen einen negativen Einfluss auf Solarmodule haben. Wenn Photonen mit Elektronen in einer Solarzelle in Kontakt kommen, setzen sie freie Elektronen frei. Bei höheren Temperaturen befinden sich jedoch bereits mehr Elektronen in einem angeregten Zustand, was die Spannung verringert, die die Module erzeugen können, und damit die Effizienz verringert.

Unter Berücksichtigung dieses Phänomens zeigt Abbildung 5 unten die Modultemperatur und die Gleichstromleistung für SP2 (Datenpunkte, bei denen die Umgebungstemperatur niedriger als die Modultemperatur ist, und Tageszeiten, zu denen das Modul mit einer niedrigeren Zahl läuft, wurden gefiltert Datenverzerrung verhindern).

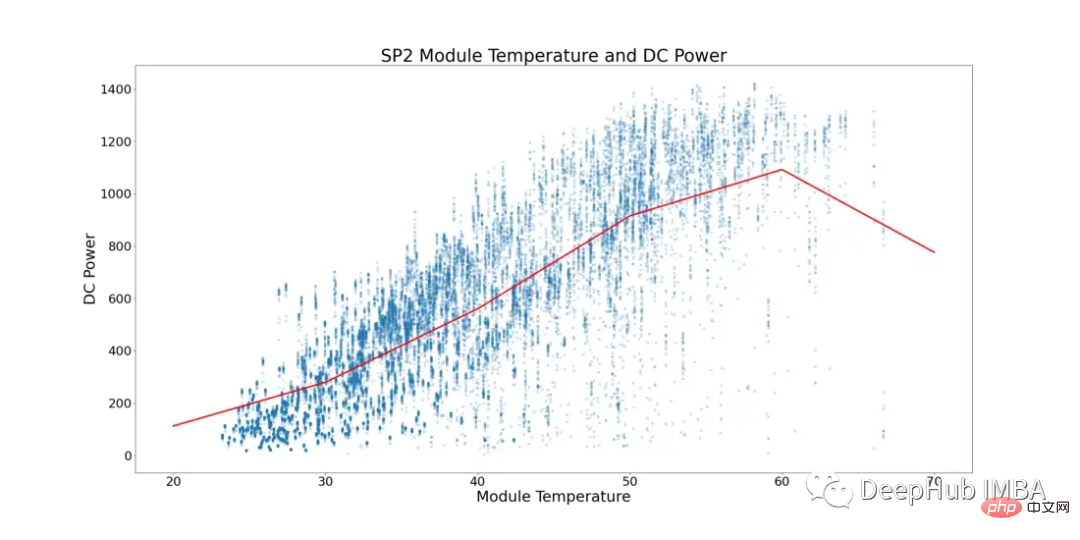
In Abbildung 5 stellt die rote Linie die Durchschnittstemperatur dar. Hier sehen Sie, dass es einen klaren Wendepunkt und Anzeichen einer Stagnation der Gleichstromversorgung gibt. Beginnt bei ~52°C ein Plateau zu erreichen. Um Solarmodule mit suboptimaler Leistung zu finden, wurden alle Zeilen entfernt, in denen Modultemperaturen über 52 °C auftraten.

Abbildung 6 unten zeigt die Gleichstromleistung jedes Moduls in SP2 im Laufe eines Tages. Dies entspricht grundsätzlich den Erwartungen und die Stromerzeugung ist zur Mittagszeit größer. Doch es gibt noch ein weiteres Problem: In Spitzenbetriebszeiten ist die Stromerzeugung gering. Es fällt uns schwer, die Gründe für diese Situation zusammenzufassen, da die Wetterbedingungen an diesem Tag möglicherweise schlecht sind oder der SP2 möglicherweise routinemäßig gewartet werden muss usw.

In Abbildung 6 gibt es auch Anzeichen für Module mit geringer Leistung. Sie können im Diagramm als Module (einzelne Datenpunkte) identifiziert werden, die vom nächstgelegenen Cluster abweichen.

Um festzustellen, welche Module leistungsschwach sind, können wir statistische Tests durchführen und dabei die Leistung jedes Moduls mit der anderer Module vergleichen, um die Leistung zu ermitteln.

Alle 15 Minuten ist die Verteilung der Gleichstromversorgungen verschiedener Module gleichzeitig eine Normalverteilung. Durch Hypothesentests kann festgestellt werden, welche Module eine schlechte Leistung erbringen. Die Anzahl gibt an, wie oft ein Modul mit einem p-Wert

Abbildung 7 zeigt in absteigender Reihenfolge, wie oft jedes Modul im gleichen Zeitraum statistisch signifikant niedriger war als andere Module.

Aus Abbildung 7 wird deutlich, dass das Modul „Quc1TzYxW2pYoWX“ problematisch ist. Diese Informationen können den zuständigen SP2-Mitarbeitern zur Untersuchung der Ursache zur Verfügung gestellt werden.

Modellierung

Nachfolgend beginnen wir mit der Modellierung und dem Vergleich mithilfe von drei verschiedenen Zeitreihenalgorithmen: SARIMA, XGBoost und CNN-LSTM.

Für alle drei Modelle können Sie den nächsten Datenpunkt mit Predict vorhersagen. Die Walk-Forward-Validierung ist eine Technik, die bei der Zeitreihenmodellierung verwendet wird, da Vorhersagen mit der Zeit ungenauer werden. Ein praktischerer Ansatz besteht daher darin, das Modell mit tatsächlichen Daten neu zu trainieren, sobald diese verfügbar sind.

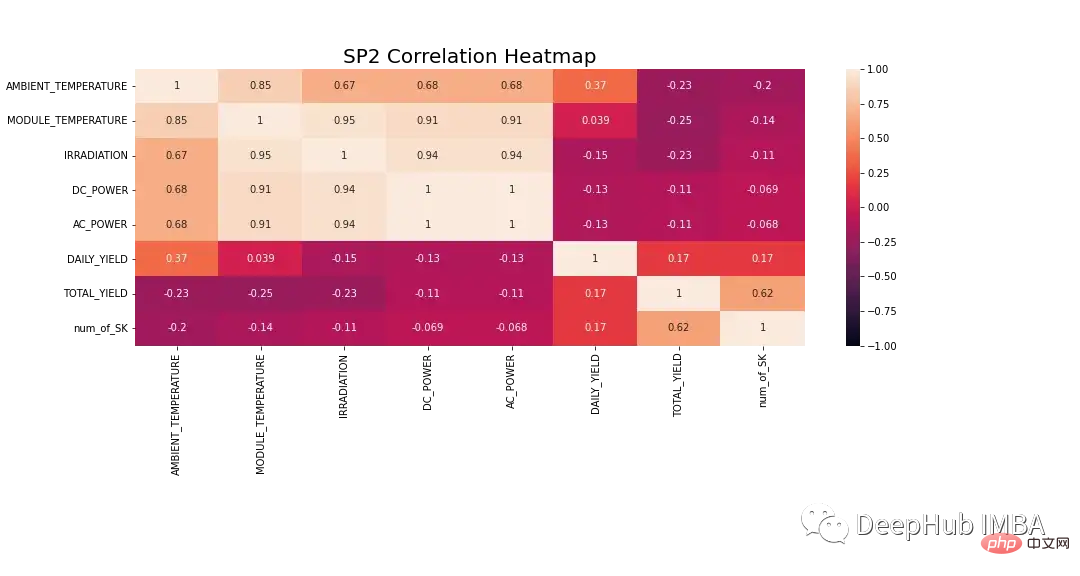
Die Daten müssen vor der Modellierung genauer untersucht werden. Abbildung 8 zeigt die Korrelations-Heatmap für alle Features im SP2-Datensatz. Die Heatmap zeigt die starke Korrelation der abhängigen Größe DC-Leistung mit Modultemperatur, Einstrahlung und Umgebungstemperatur. Diese Eigenschaften können bei der Vorhersage eine wichtige Rolle spielen.

In der Wärmekarte unten weist Wechselstrom einen Pearson-Korrelationskoeffizienten von 1 auf. Um Datenlecks vorzubeugen, trennen wir die Daten von der Gleichstromversorgung.

SARIMA

Seasonal Autoregressive Integrated Moving Average (SARIMA) ist eine univariate Zeitreihen-Prognosemethode. Da die Zielvariable Anzeichen eines 24-Stunden-Zyklus aufweist, ist SARIMA eine effiziente Modellierungsoption, da es saisonale Effekte berücksichtigt. Dies kann in der saisonalen Aufschlüsselungstabelle unten beobachtet werden.

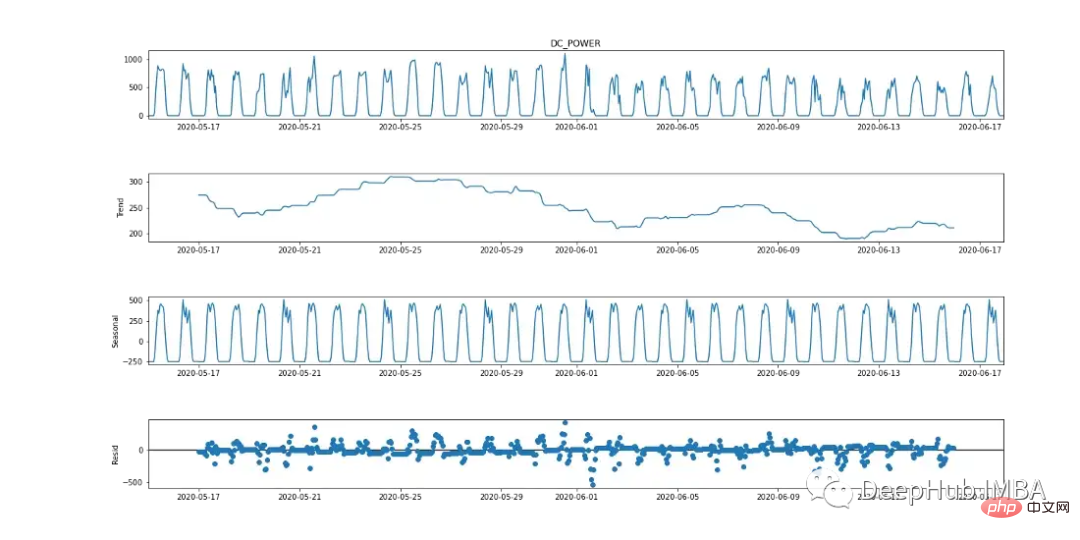
Der SARIMA-Algorithmus erfordert, dass die Daten stationär sind. Es gibt verschiedene Methoden, um zu testen, ob Daten stationär sind, z. B. statistische Tests (erweiterter Dickey-Fowler-Test), zusammenfassende Statistiken (Vergleich von Mittelwerten/Varianzen verschiedener Teile der Daten) und die visuelle Analyse der Daten. Es ist wichtig, vor der Modellierung mehrere Tests durchzuführen.

Der Augmented Dickey-Fuller (ADF)-Test ist ein „Einheitswurzeltest“, der verwendet wird, um zu bestimmen, ob eine Zeitreihe stationär ist. Im Grunde handelt es sich um einen statistischen Signifikanztest, bei dem eine Nullhypothese und eine Alternativhypothese vorliegen und auf der Grundlage des resultierenden p-Werts eine Schlussfolgerung gezogen wird.

Nullhypothese: Zeitreihendaten sind instationär.

Alternativhypothese: Zeitreihendaten sind stationär.

Wenn in unserem Beispiel der p-Wert ≤ 0,05 ist, können wir die Nullhypothese ablehnen und bestätigen, dass die Daten keine Einheitswurzel haben.

 from statsmodels.tsa.stattools import adfuller
 
 result = adfuller(plant2_dcpower.values)
 
 print('ADF Statistic: %f' % result[0])
 print('p-value: %f' % result[1])
 print('Critical Values:')
 for key, value in result[4].items():
print('t%s: %.3f' % (key, value))

Aus dem ADF-Test beträgt der p-Wert 0,000553,

Um die abhängige Variable mit SARIMA zu modellieren, muss die Zeitreihe stationär sein. Wie in Abbildung 9 (erstes und drittes Diagramm) dargestellt, weist Gleichstrom deutliche Anzeichen von Saisonalität auf. Nehmen Sie die erste Differenz [t-(t-1)], um die saisonale Komponente zu entfernen, wie in Abbildung 10 dargestellt, da sie einer Normalverteilung ähnelt. Die Daten sind nun stationär und für den SARIMA-Algorithmus geeignet.

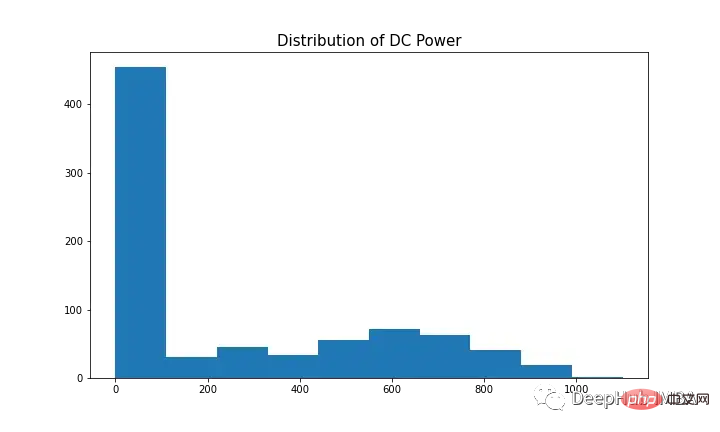
SARIMAs Hyperparameter umfassen p (autoregressive Ordnung), d (Differenzordnung), q (gleitende Durchschnittsordnung), p (saisonale autoregressive Ordnung), d (saisonale Differenzordnung), q (saisonale gleitende Durchschnittsordnung), m (Zeitschritt des saisonalen Zyklus), Trend (deterministischer Trend).

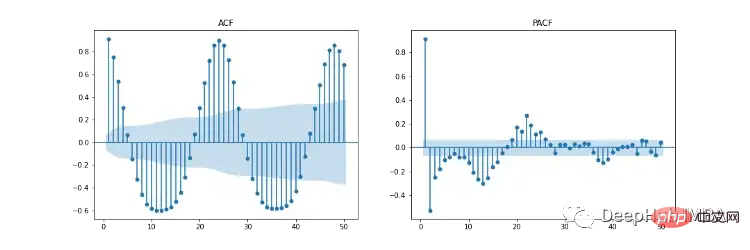
Abbildung 11 zeigt die Diagramme der Autokorrelation (ACF), der partiellen Autokorrelation (PACF) und der saisonalen ACF/PACF. Das ACF-Diagramm zeigt die Korrelation zwischen einer Zeitreihe und ihrer verzögerten Version. PACF zeigt eine direkte Korrelation zwischen einer Zeitreihe und ihrer verzögerten Version. Der blau schattierte Bereich stellt das Konfidenzintervall dar. SACF und SPACF können berechnet werden, indem die saisonale Differenz (m) aus den Originaldaten herangezogen wird, in diesem Fall 24, da es im ACF-Diagramm einen offensichtlichen 24-Stunden-Saisoneffekt gibt.

Nach unserer Intuition kann der Startpunkt der Hyperparameter aus den ACF- und PACF-Diagrammen abgeleitet werden. Beispielsweise zeigen sowohl ACF als auch PACF einen allmählichen Abwärtstrend, d. h. die autoregressive Ordnung (p) und die Ordnung des gleitenden Durchschnitts (q) sind beide größer als 0. p und p können bestimmt werden, indem man sich die PCF- bzw. SPCF-Diagramme ansieht und die Anzahl der Verzögerungen zählt, die statistisch signifikant werden, bevor der Verzögerungswert unbedeutend wird. Ebenso sind q und q in ACF- und SACF-Diagrammen zu finden.

Die Differenzordnung (d) kann durch die Anzahl der Differenzen bestimmt werden, die die Daten stationär machen. Die Reihenfolge der saisonalen Differenz (D) wird anhand der Anzahl der Differenzen geschätzt, die erforderlich sind, um die saisonale Komponente aus der Zeitreihe zu entfernen.

Sie können diesen Artikel für diese Hyperparameterauswahl lesen: https://arauto.readthedocs.io/en/latest/how_to_choose_terms.html

Sie können auch die Rastersuchmethode zur Hyperparameteroptimierung verwenden, basierend auf dem minimalen mittleren quadratischen Fehler (MSE) ) Wählen Sie die optimalen Hyperparameter aus, einschließlich p = 2, d = 0, q = 4, p = 2, d = 1, q = 6, m = 24, Trend = 'n' (kein Trend).

from time import time
 from sklearn.metrics import mean_squared_error
 from statsmodels.tsa.statespace.sarimax import SARIMAX
 
 configg = [(2, 1, 4), (2, 1, 6, 24), 'n']
 
 def train_test_split(data, test_len=48):
"""
Split data into training and testing.
"""
train, test = data[:-test_len], data[-test_len:]
return train, test
 
 def sarima_model(data, cfg, test_len, i):
"""
SARIMA model which outputs prediction and model.
"""
order, s_order, t = cfg[0], cfg[1], cfg[2]
model = SARIMAX(data, order=order, seasonal_order=s_order, trend=t,
enforce_stationarity=False, enfore_invertibility=False)
model_fit = model.fit(disp=False)
yhat = model_fit.predict(len(data))
 
if i + 1 == test_len:
return yhat, model_fit
else:
return yhat
 
 def walk_forward_val(data, cfg):
"""
A walk forward validation technique used for time series data. Takes current value of x_test and predicts
value. x_test is then fed back into history for the next prediction.
"""
train, test = train_test_split(data)
pred = []
history = [i for i in train]
test_len = len(test)
 
for i in range(test_len):
if i + 1 == test_len:
yhat, s_model = sarima_model(history, cfg, test_len, i)
pred.append(yhat)
mse = mean_squared_error(test, pred)
return pred, mse, s_model
else:
yhat = sarima_model(history, cfg, test_len, i)
pred.append(yhat)
history.append(test[i])
pass
 
 if __name__ == '__main__':
start_time = time()
sarima_pred_plant2, sarima_mse, s_model = walk_forward_val(plant2_dcpower, configg)
time_len = time() - start_time
 
print(f'SARIMA runtime: {round(time_len/60,2)} mins')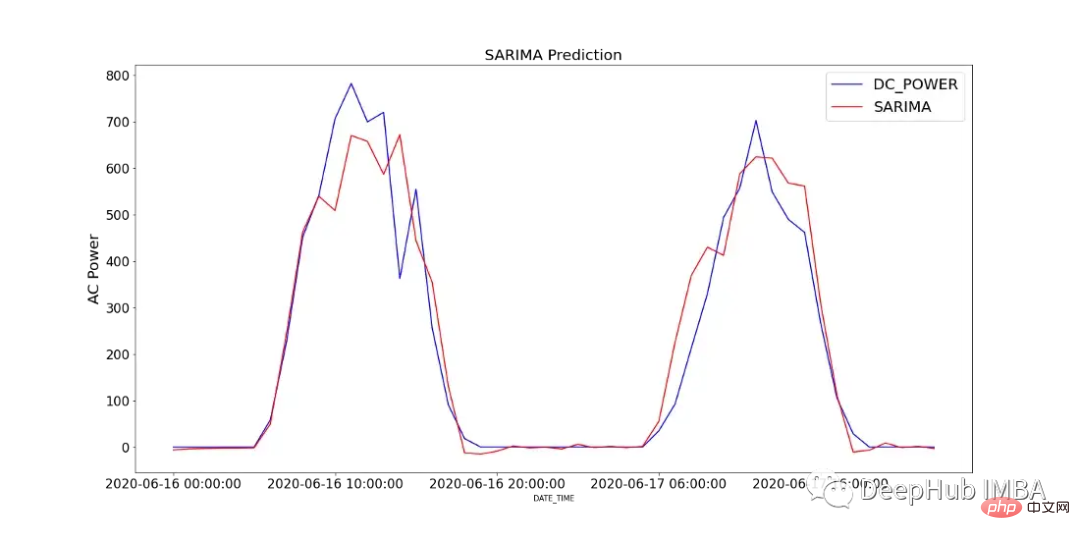

Abbildung 12 zeigt den Vergleich der vorhergesagten Werte des SARIMA-Modells mit der über 2 Tage in SP2 aufgezeichneten Gleichstromleistung.

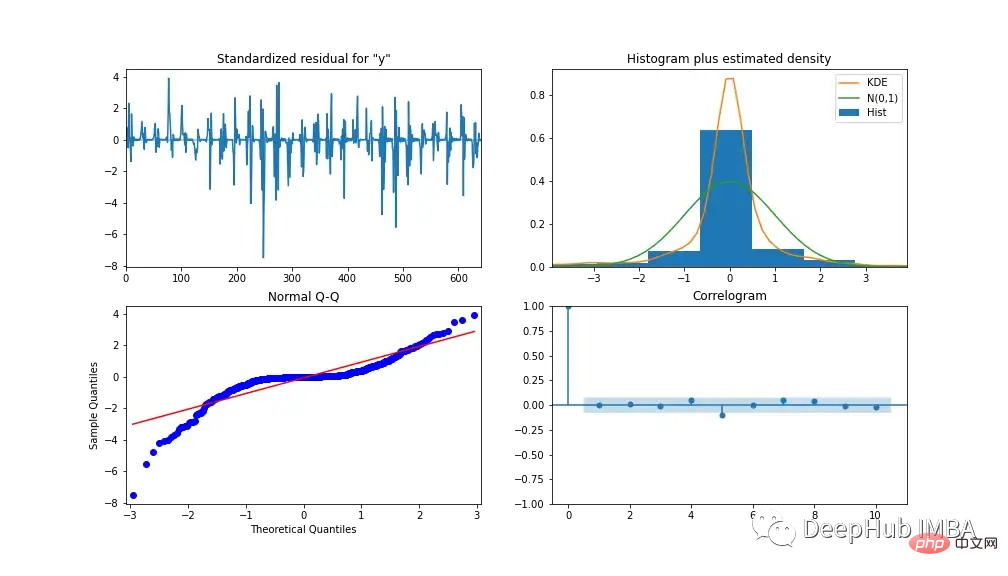
Um die Leistung des Modells zu analysieren, zeigt Abbildung 13 die Modelldiagnose. Das Korrelationsdiagramm zeigt nach der ersten Verzögerung fast keine Korrelation und das Histogramm unten zeigt eine Normalverteilung um den Mittelwert Null. Daraus können wir schließen, dass das Modell keine weiteren Informationen aus den Daten gewinnen kann.

XGBoost

XGBoost (eXtreme Gradient Boosting) ist ein Entscheidungsbaumalgorithmus zur Gradientenverstärkung. Es verwendet einen Ensemble-Ansatz, bei dem neue Entscheidungsbaummodelle hinzugefügt werden, um vorhandene Entscheidungsbaumbewertungen zu ändern. Im Gegensatz zu SARIMA ist XGBoost ein multivariater Algorithmus für maschinelles Lernen, was bedeutet, dass das Modell mehrere Funktionen übernehmen kann, um die Modellleistung zu verbessern.

Wir nutzen Feature Engineering, um die Modellgenauigkeit zu verbessern. Außerdem wurden drei zusätzliche Merkmale erstellt, darunter nacheilende Versionen der AC- und DC-Leistung, S1_AC_POWER bzw. S1_DC_POWER, und der Gesamtwirkungsgrad EFF, bei dem es sich um die AC-Leistung dividiert durch die DC-Leistung handelt. Und entfernen Sie AC_POWER und MODULE_TEMPERATURE aus den Daten. Abbildung 14 zeigt die Feature-Wichtigkeitsstufe nach Verstärkung (durchschnittliche Verstärkung der Aufteilung mithilfe einer Funktion) und Gewichtung (Häufigkeit, wie oft eine Funktion im Baum erscheint).

Bestimmen Sie die bei der Modellierung verwendeten Hyperparameter durch Rastersuche. Die Ergebnisse sind: *Lernrate = 0,01, Anzahl der Schätzer = 1200, Unterstichprobe = 0,8, Kolsample nach Baum = 1, Kolsample nach Ebene = 1, minimales Kindergewicht = 20 und maximale Tiefe = 10

Wir verwenden MinMaxScaler, um die Trainingsdaten auf einen Wert zwischen 0 und 1 zu skalieren (Sie können je nach Verteilung der Daten auch mit anderen Skalierern wie Log-Transformation und Standardskalierer experimentieren). Wandeln Sie die Daten in einen überwachten Lerndatensatz um, indem Sie alle unabhängigen Variablen um eine bestimmte Zeitspanne nach hinten verschieben.

 import numpy as np
 import pandas as pd
 import xgboost as xgb
 from sklearn.preprocessing import MinMaxScaler
 from time import time
 
 def train_test_split(df, test_len=48):
"""
split data into training and testing.
"""
train, test = df[:-test_len], df[-test_len:]
return train, test
 
 def data_to_supervised(df, shift_by=1, target_var='DC_POWER'):
"""
Convert data into a supervised learning problem.
"""
target = df[target_var][shift_by:].values
dep = df.drop(target_var, axis=1).shift(-shift_by).dropna().values
data = np.column_stack((dep, target))
return data
 
 
 def xgb_forecast(train, x_test):
"""
XGBOOST model which outputs prediction and model.
"""
x_train, y_train = train[:,:-1], train[:,-1]
xgb_model = xgb.XGBRegressor(learning_rate=0.01, n_estimators=1500, subsample=0.8,
colsample_bytree=1, colsample_bylevel=1,
min_child_weight=20, max_depth=14, objective='reg:squarederror')
xgb_model.fit(x_train, y_train)
yhat = xgb_model.predict([x_test])
return yhat[0], xgb_model
 
 def walk_forward_validation(df):
"""
A walk forward validation approach by scaling the data and changing into a supervised learning problem.
"""
preds = []
train, test = train_test_split(df)
 
scaler = MinMaxScaler(feature_range=(0,1))
train_scaled = scaler.fit_transform(train)
test_scaled = scaler.transform(test)
 
train_scaled_df = pd.DataFrame(train_scaled, columns = train.columns, index=train.index)
test_scaled_df = pd.DataFrame(test_scaled, columns = test.columns, index=test.index)
 
train_scaled_sup, test_scaled_sup = data_to_supervised(train_scaled_df), data_to_supervised(test_scaled_df)
history = np.array([x for x in train_scaled_sup])
 
for i in range(len(test_scaled_sup)):
test_x, test_y = test_scaled_sup[i][:-1], test_scaled_sup[i][-1]
yhat, xgb_model = xgb_forecast(history, test_x)
preds.append(yhat)
np.append(history,[test_scaled_sup[i]], axis=0)
 
pred_array = test_scaled_df.drop("DC_POWER", axis=1).to_numpy()
pred_num = np.array([pred])
pred_array = np.concatenate((pred_array, pred_num.T), axis=1)
result = scaler.inverse_transform(pred_array)
 
return result, test, xgb_model
 
 if __name__ == '__main__':
start_time = time()
xgb_pred, actual, xgb_model = walk_forward_validation(dropped_df_cat)
time_len = time() - start_time
 
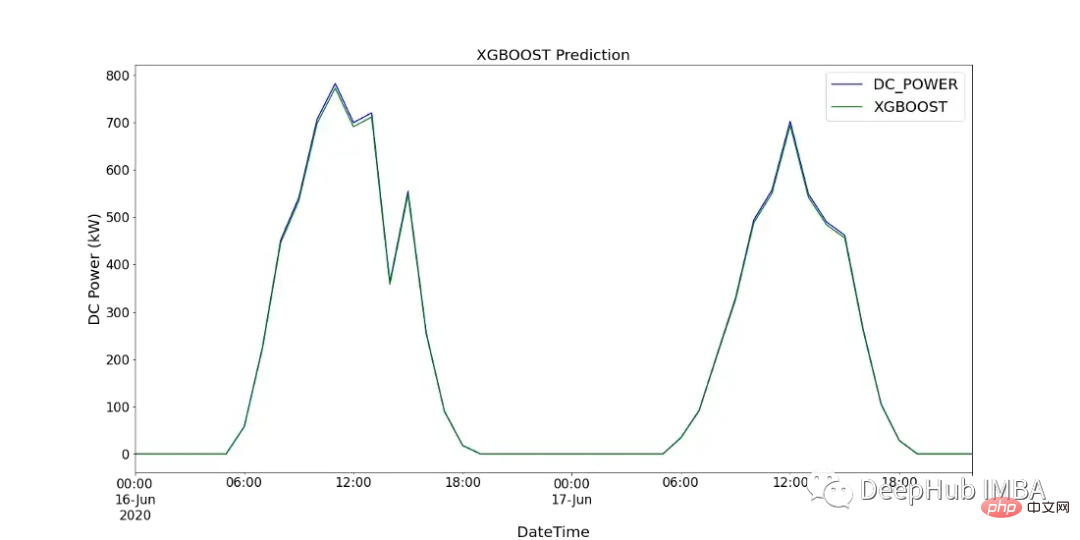
print(f'XGBOOST runtime: {round(time_len/60,2)} mins')

图15显示了XGBoost模型的预测值与SP2 2天内记录的直流功率的比较。

CNN-LSTM

CNN-LSTM (convolutional Neural Network Long - Short-Term Memory)是两种神经网络模型的混合模型。CNN是一种前馈神经网络，在图像处理和自然语言处理方面表现出了良好的性能。它还可以有效地应用于时间序列数据的预测。LSTM是一种序列到序列的神经网络模型，旨在解决长期存在的梯度爆炸/消失问题，使用内部存储系统，允许它在输入序列上积累状态。

在本例中，使用CNN-LSTM作为编码器-解码器体系结构。由于CNN不直接支持序列输入，所以我们通过1D CNN读取序列输入并自动学习重要特征。然后LSTM进行解码。与XGBoost模型类似，使用scikitlearn的MinMaxScaler使用相同的数据并进行缩放，但范围在-1到1之间。对于CNN-LSTM，需要将数据重新整理为所需的结构:[samples, subsequences, timesteps, features]，以便可以将其作为输入传递给模型。

由于我们希望为每个子序列重用相同的CNN模型，因此使用timedidistributedwrapper对每个输入子序列应用一次整个模型。在下面的图16中可以看到最终模型中使用的不同层的模型摘要。

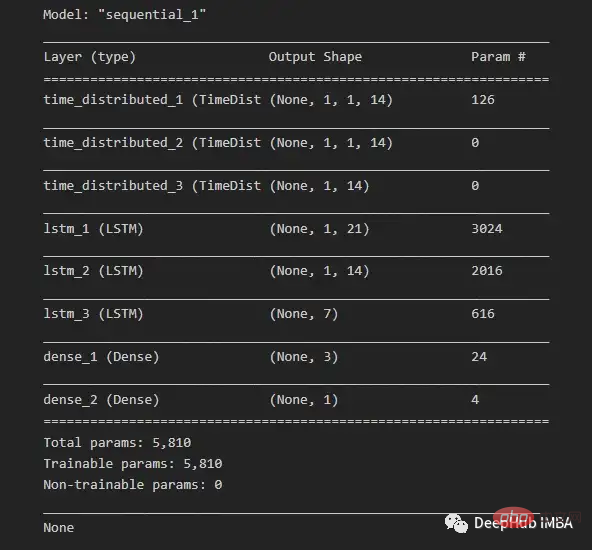
在将数据分解为训练数据和测试数据之后，将训练数据分解为训练数据和验证数据集。在所有训练数据(包括验证数据)的每次迭代之后，模型可以进一步使用这一点来评估模型的性能。

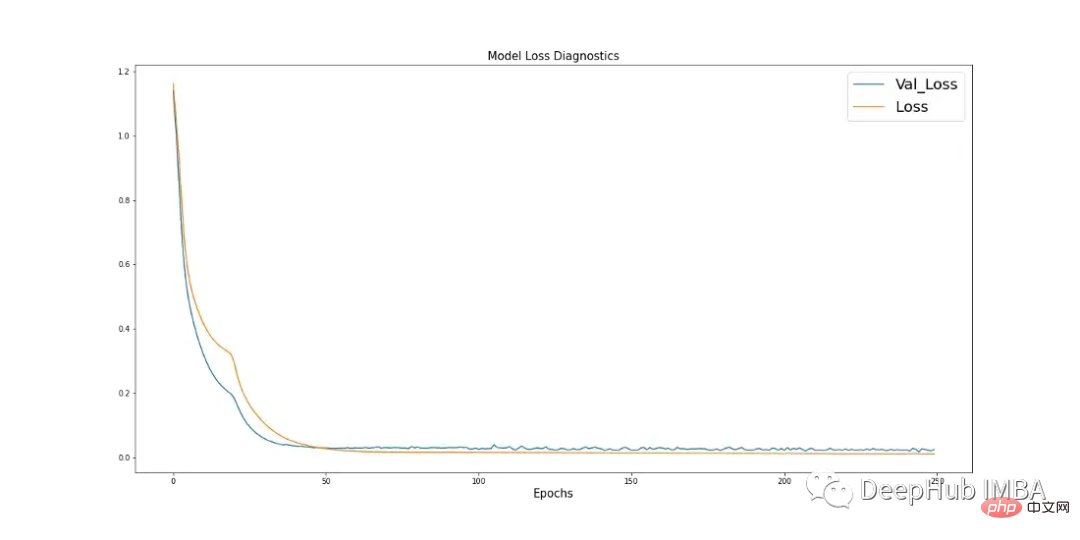
学习曲线是深度学习中使用的一个很好的诊断工具，它显示了模型在每个阶段之后的表现。下面的图17显示了模型如何从数据中学习，并显示了验证数据与训练数据的收敛。这是良好模特训练的标志。

import pandas as pd
 import numpy as np
 from sklearn.metrics import mean_squared_error
 from sklearn.preprocessing import MinMaxScaler
 import keras
 from keras.models import Sequential
 from keras.layers.convolutional import Conv1D, MaxPooling1D
 from keras.layers import LSTM, TimeDistributed, RepeatVector, Dense, Flatten
 from keras.optimizers import Adam
 
 n_steps = 1
 subseq = 1
 
 def train_test_split(df, test_len=48):
"""
Split data in training and testing. Use 48 hours as testing.
"""
train, test = df[:-test_len], df[-test_len:]
return train, test
 
 def split_data(sequences, n_steps):
"""
Preprocess data returning two arrays.
"""
x, y = [], []
for i in range(len(sequences)):
end_x = i + n_steps
 
if end_x > len(sequences):
break
x.append(sequences[i:end_x, :-1])
y.append(sequences[end_x-1, -1])
 
return np.array(x), np.array(y)
 
def CNN_LSTM(x, y, x_val, y_val):
"""
CNN-LSTM model.
"""
model = Sequential()
model.add(TimeDistributed(Conv1D(filters=14, kernel_size=1, activation="sigmoid",
input_shape=(None, x.shape[2], x.shape[3]))))
model.add(TimeDistributed(MaxPooling1D(pool_size=1)))
model.add(TimeDistributed(Flatten()))
model.add(LSTM(21, activation="tanh", return_sequences=True))
model.add(LSTM(14, activation="tanh", return_sequences=True))
model.add(LSTM(7, activation="tanh"))
model.add(Dense(3, activation="sigmoid"))
model.add(Dense(1))
 
model.compile(optimizer=Adam(learning_rate=0.001), loss="mse", metrics=['mse'])
history = model.fit(x, y, epochs=250, batch_size=36,
verbose=0, validation_data=(x_val, y_val))
 
return model, history
 
 # split and resahpe data
 train, test = train_test_split(dropped_df_cat)
 
 train_x = train.drop(columns="DC_POWER", axis=1).to_numpy()
 train_y = train["DC_POWER"].to_numpy().reshape(len(train), 1)
 
 test_x = test.drop(columns="DC_POWER", axis=1).to_numpy()
 test_y = test["DC_POWER"].to_numpy().reshape(len(test), 1)
 
 #scale data
 scaler_x = MinMaxScaler(feature_range=(-1,1))
 scaler_y = MinMaxScaler(feature_range=(-1,1))
 
 train_x = scaler_x.fit_transform(train_x)
 train_y = scaler_y.fit_transform(train_y)
 
 test_x = scaler_x.transform(test_x)
 test_y = scaler_y.transform(test_y)
 
 
 # shape data into CNN-LSTM format [samples, subsequences, timesteps, features] ORIGINAL
 train_data_np = np.hstack((train_x, train_y))
 x, y = split_data(train_data_np, n_steps)
 x_subseq = x.reshape(x.shape[0], subseq, x.shape[1], x.shape[2])
 
 # create validation set
 x_val, y_val = x_subseq[-24:], y[-24:]
 x_train, y_train = x_subseq[:-24], y[:-24]
 
 n_features = x.shape[2]
 actual = scaler_y.inverse_transform(test_y)
 
 # run CNN-LSTM model
 if __name__ == '__main__':
start_time = time()
 
model, history = CNN_LSTM(x_train, y_train, x_val, y_val)
prediction = []
 
for i in range(len(test_x)):
test_input = test_x[i].reshape(1, subseq, n_steps, n_features)
yhat = model.predict(test_input, verbose=0)
yhat_IT = scaler_y.inverse_transform(yhat)
prediction.append(yhat_IT[0][0])
 
time_len = time() - start_time
mse = mean_squared_error(actual.flatten(), prediction)
 
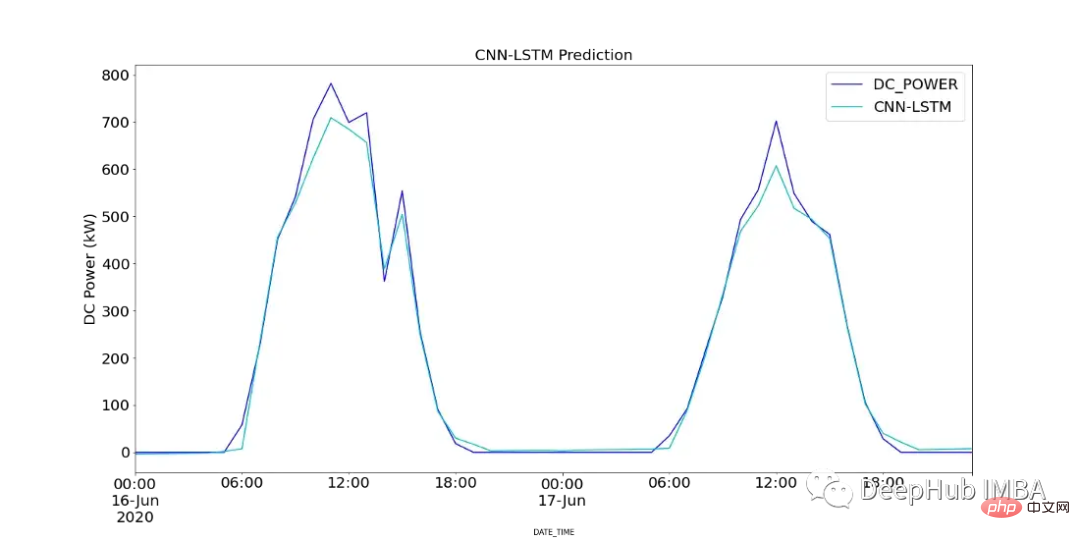
print(f'CNN-LSTM runtime: {round(time_len/60,2)} mins')
print(f"CNN-LSTM MSE: {round(mse,2)}")

图18显示了CNN-LSTM模型的预测值与SP2 2天内记录的直流功率的对比。

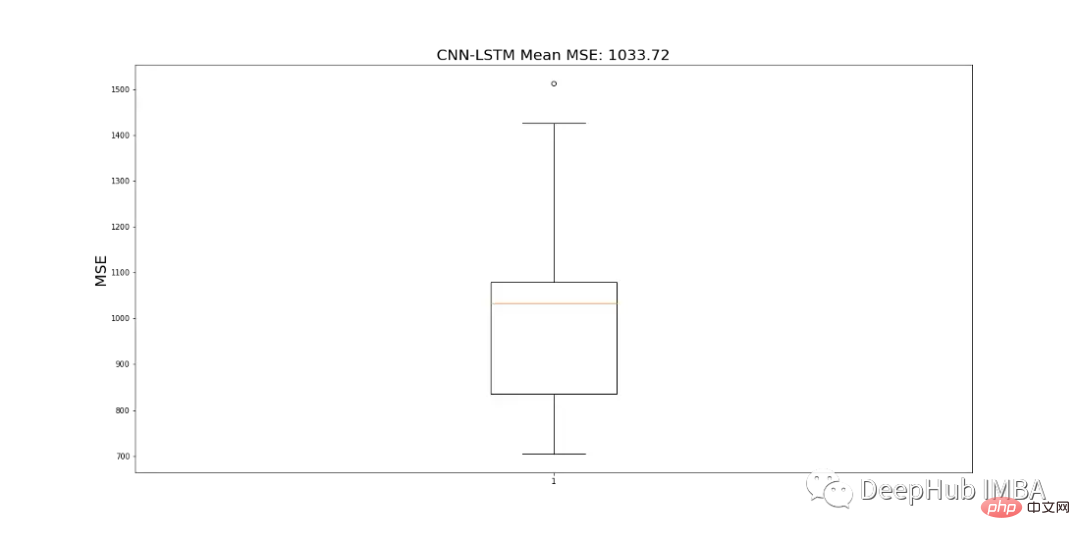
由于CNN-LSTM的随机性，该模型运行10次，并记录一个平均MSE值作为最终值，以判断模型的性能。图19显示了为所有模型运行记录的mse的范围。

结果对比

下表显示了每个模型的MSE (CNN-LSTM的平均MSE)和每个模型的运行时间(以分钟为单位)。

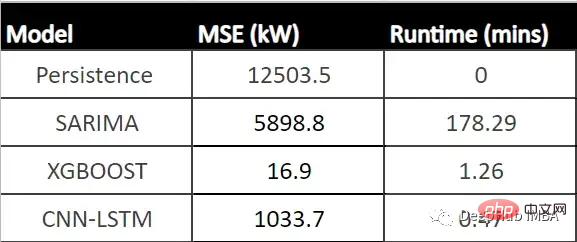
从表中可以看出，XGBoost的MSE最低、运行时第二快，并且与所有其他模型相比具有最佳性能。由于该模型显示了一个可以接受的每小时预测的运行时，它可以成为帮助运营经理决策过程的强大工具。

总结

在本文中我们分析了SP1和SP2，确定SP1性能较低。所以对SP2的进一步调查显示，并且查看了SP2中那些模块性能可能有问题，并使用假设检验来计算每个模块在统计上明显表现不佳的次数，' Quc1TzYxW2pYoWX '模块显示了约850次低性能计数。

我们使用数据训练三个模型：SARIMA、XGBoost和CNN-LSTM。SARIMA表现最差，XGBOOST表现最好，MSE为16.9，运行时间为1.43 min。所以可以说XGBoost在表格数据中还是最优先得选择。

Das obige ist der detaillierte Inhalt vonVergleichen Sie Zeitreihenvorhersagemethoden basierend auf SARIMA, XGBoost und CNN-LSTM.. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!