Vergleich gängiger Technologien zur Dimensionsreduzierung: Machbarkeitsanalyse zur Reduzierung der Datendimensionen bei gleichzeitiger Wahrung der Informationsintegrität

In diesem Artikel wird die Wirksamkeit verschiedener Techniken zur Dimensionsreduktion bei Tabellendaten bei maschinellen Lernaufgaben verglichen. Wir wenden Dimensionsreduktionsmethoden auf den Datensatz an und bewerten ihre Wirksamkeit durch Regressions- und Klassifizierungsanalysen. Wir wenden Dimensionsreduktionsmethoden auf verschiedene von UCI erhaltene Datensätze an, die sich auf verschiedene Domänen beziehen. Insgesamt wurden 15 Datensätze ausgewählt, von denen 7 für die Regression und 8 für die Klassifizierung verwendet werden.

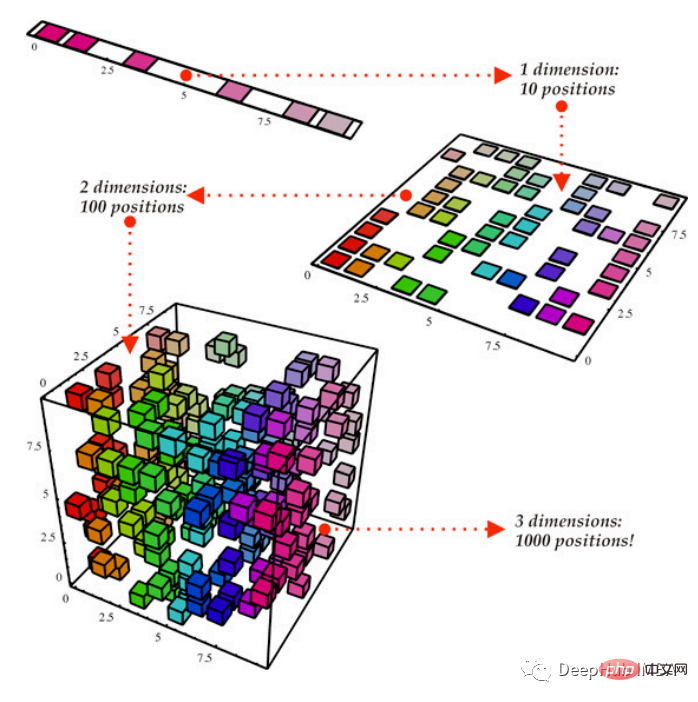
Um diesen Artikel leichter lesbar und verständlich zu machen, wird nur die Vorverarbeitung und Analyse eines Datensatzes gezeigt. Das Experiment beginnt mit dem Laden des Datensatzes. Der Datensatz wird in Trainings- und Testsätze aufgeteilt und dann normalisiert, um einen Mittelwert von 0 und eine Standardabweichung von 1 zu haben.

Techniken zur Dimensionsreduktion werden dann auf die Trainingsdaten angewendet und der Testsatz wird zur Dimensionsreduktion unter Verwendung derselben Parameter transformiert. Für die Regression werden Hauptkomponentenanalyse (PCA) und Singular Value Decomposition (SVD) zur Dimensionsreduktion verwendet. Für die Klassifizierung wird hingegen die lineare Diskriminanzanalyse (LDA) verwendet. Nach der Dimensionsreduktion werden mehrere Modelle für maschinelles Lernen trainiert Testen und Vergleichen der Leistung verschiedener Modelle an verschiedenen Datensätzen, die mit verschiedenen Dimensionsreduktionsmethoden erhalten wurden.

Datenverarbeitung

Lassen Sie uns den Prozess beginnen, indem wir den ersten Datensatz laden,

import pandas as pd ## for data manipulation
df = pd.read_excel(r'RegressionAirQualityUCI.xlsx')
print(df.shape)
df.head()

Der Datensatz enthält 15 Spalten, von denen eine zur Vorhersage der Bezeichnung erforderlich ist. Bevor mit der Dimensionsreduzierung fortgefahren wird, werden auch die Datums- und Uhrzeitspalten entfernt.

X = df.drop(['CO(GT)', 'Date', 'Time'], axis=1)
y = df['CO(GT)']
X.shape, y.shape

#Output: ((9357, 12), (9357,))

Für das Training müssen wir den Datensatz in einen Trainingssatz und einen Testsatz unterteilen, damit die Wirksamkeit der Dimensionsreduktionsmethode und des auf dem Dimensionsreduktionsmerkmalsraum trainierten Modells für maschinelles Lernen bewertet werden kann. Das Modell wird mit dem Trainingssatz trainiert und die Leistung wird mit dem Testsatz bewertet.

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
X_train.shape, X_test.shape, y_train.shape, y_test.shape

#Output: ((7485, 12), (1872, 12), (7485,), (1872,))

Bevor Techniken zur Dimensionsreduktion auf den Datensatz angewendet werden, können die Eingabedaten skaliert werden, um sicherzustellen, dass alle Features den gleichen Maßstab haben. Dies ist für lineare Modelle von entscheidender Bedeutung, da einige Methoden zur Dimensionsreduktion ihre Ausgabe abhängig davon ändern können, ob die Daten normalisiert sind, und empfindlich auf die Größe der Features reagieren.

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
X_train.shape, X_test.shape

Hauptkomponentenanalyse (PCA)

Die PCA-Methode der linearen Dimensionsreduktion reduziert die Dimensionalität der Daten und behält gleichzeitig so viel Datenvarianz wie möglich bei.

Hier wird die PCA-Methode des Python-Moduls sklearn.decomposition verwendet. Über diesen Parameter wird die Anzahl der beizubehaltenden Komponenten angegeben, und diese Zahl beeinflusst, wie viele Dimensionen im kleineren Feature-Raum enthalten sind. Alternativ können wir eine Zielvarianz zum Beibehalten festlegen, die die Anzahl der Komponenten basierend auf der Varianzmenge in den erfassten Daten festlegt, die wir hier auf 0,95 festlegen Die Komponentenanalyse (PCA) projiziert die Daten in einen niedrigdimensionalen Raum und versucht, so viele Unterschiede in den Daten wie möglich beizubehalten. Dies kann zwar bei bestimmten Vorgängen hilfreich sein, es kann jedoch auch dazu führen, dass die Daten schwieriger zu verstehen sind. PCA kann neue Achsen in den Daten identifizieren, bei denen es sich um lineare Fusionen der ursprünglichen Merkmale handelt.

Singular Value Decomposition (SVD)

SVD ist eine lineare Dimensionsreduktionstechnik, die Merkmale mit geringer Datenvarianz in einen niedrigdimensionalen Raum projiziert. Wir müssen die Anzahl der Komponenten festlegen, die nach der Dimensionsreduzierung beibehalten werden sollen. Hier reduzieren wir die Dimensionalität um 2/3.

from sklearn.decomposition import PCA
pca = PCA(n_compnotallow=0.95)
X_train_pca = pca.fit_transform(X_train)
X_test_pca = pca.transform(X_test)
X_train_pca

Training des Regressionsmodells

Jetzt beginnen wir mit dem Training und Testen des Modells mithilfe der oben genannten drei Datentypen (Originaldatensatz, PCA und SVD) und verwenden mehrere Modelle zum Vergleich.

from sklearn.decomposition import TruncatedSVD
svd = TruncatedSVD(n_compnotallow=int(X_train.shape[1]*0.33))
X_train_svd = svd.fit_transform(X_train)
X_test_svd = svd.transform(X_test)
X_train_svd

train_test_ML: Diese Funktion erledigt die sich wiederholenden Aufgaben im Zusammenhang mit dem Training und Testen des Modells. Die Leistung aller Modelle wurde durch Berechnung von rmse und r2_score bewertet. und gibt einen Datensatz mit allen Details und berechneten Werten zurück. Außerdem wird die Zeit protokolliert, die jedes Modell zum Trainieren und Testen seines jeweiligen Datensatzes benötigt hat.

import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.neighbors import KNeighborsRegressor
from sklearn.svm import SVR
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor
from sklearn.metrics import r2_score, mean_squared_error
import time

Originaldaten:

def train_test_ML(dataset, dataform, X_train, y_train, X_test, y_test):
temp_df = pd.DataFrame(columns=['Data Set', 'Data Form', 'Dimensions', 'Model', 'R2 Score', 'RMSE', 'Time Taken'])
for i in [LinearRegression, KNeighborsRegressor, SVR, DecisionTreeRegressor, RandomForestRegressor, GradientBoostingRegressor]:
start_time = time.time()
reg = i().fit(X_train, y_train)
y_pred = reg.predict(X_test)
r2 = np.round(r2_score(y_test, y_pred), 2)
rmse = np.round(np.sqrt(mean_squared_error(y_test, y_pred)), 2)
end_time = time.time()
time_taken = np.round((end_time - start_time), 2)
temp_df.loc[len(temp_df)] = [dataset, dataform, X_train.shape[1], str(i).split('.')[-1][:-2], r2, rmse, time_taken]
return temp_df

Es ist ersichtlich, dass der KNN-Regressor und der Random Forest bei der Eingabe von Originaldaten relativ gut funktionieren und die Trainingszeit des Random Forest am längsten ist.

PCA

original_df = train_test_ML('AirQualityUCI', 'Original', X_train, y_train, X_test, y_test)
original_df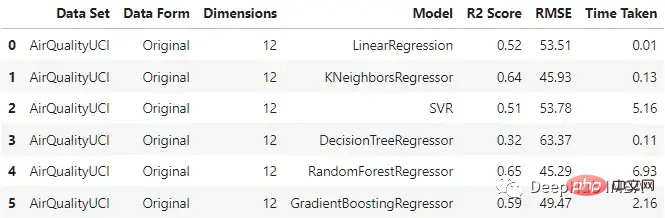

与原始数据集相比，不同模型的性能有不同程度的下降。梯度增强回归和支持向量回归在两种情况下保持了一致性。这里一个主要的差异也是预期的是模型训练所花费的时间。与其他模型不同的是，SVR在这两种情况下花费的时间差不多。

SVD

svd_df = train_test_ML('AirQualityUCI', 'SVD Reduced', X_train_svd, y_train, X_test_svd, y_test)
svd_df

与PCA相比，SVD以更大的比例降低了维度，随机森林和梯度增强回归器的表现相对优于其他模型。

回归模型分析

对于这个数据集，使用主成分分析时，数据维数从12维降至5维，使用奇异值分析时，数据降至3维。

• 就机器学习性能而言，数据集的原始形式相对更好。造成这种情况的一个潜在原因可能是，当我们使用这种技术降低维数时，在这个过程中会发生信息损失。
• 但是线性回归、支持向量回归和梯度增强回归在原始和PCA案例中的表现是一致的。
• 在我们通过SVD得到的数据上，所有模型的性能都下降了。
• 在降维情况下，由于特征变量的维数较低，模型所花费的时间减少了。

将类似的过程应用于其他六个数据集进行测试，得到以下结果:

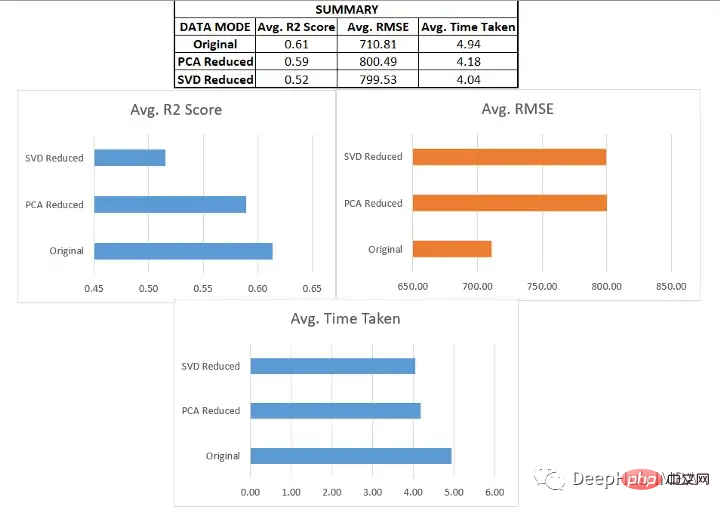
我们在各种数据集上使用了SVD和PCA，并对比了在原始高维特征空间上训练的回归模型与在约简特征空间上训练的模型的有效性

• 原始数据集始终优于由降维方法创建的低维数据。这说明在降维过程中可能丢失了一些信息。
• 当用于更大的数据集时，降维方法有助于显著减少数据集中的特征数量，从而提高机器学习模型的有效性。对于较小的数据集，改影响并不显著。
• 模型的性能在original和pca_reduced两种模式下保持一致。如果一个模型在原始数据集上表现得更好，那么它在PCA模式下也会表现得更好。同样，较差的模型也没有得到改进。
• 在SVD的情况下，模型的性能下降比较明显。这可能是n_components数量选择的问题，因为太小数量肯定会丢失数据。
• 决策树在SVD数据集时一直是非常差的，因为它本来就是一个弱学习器

训练分类模型

对于分类我们将使用另一种降维方法：LDA。机器学习和模式识别任务经常使用被称为线性判别分析(LDA)的降维方法。这种监督学习技术旨在最大化几个类或类别之间的距离，同时将数据投影到低维空间。由于它的作用是最大化类之间的差异，因此只能用于分类任务。

from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn.metrics import accuracy_score, f1_score, recall_score, precision_score

继续我们的训练方法

def train_test_ML2(dataset, dataform, X_train, y_train, X_test, y_test):
temp_df = pd.DataFrame(columns=['Data Set', 'Data Form', 'Dimensions', 'Model', 'Accuracy', 'F1 Score', 'Recall', 'Precision', 'Time Taken'])
for i in [LogisticRegression, KNeighborsClassifier, SVC, DecisionTreeClassifier, RandomForestClassifier, GradientBoostingClassifier]:
start_time = time.time()
reg = i().fit(X_train, y_train)
y_pred = reg.predict(X_test)
accuracy = np.round(accuracy_score(y_test, y_pred), 2)
f1 = np.round(f1_score(y_test, y_pred, average='weighted'), 2)
recall = np.round(recall_score(y_test, y_pred, average='weighted'), 2)
precision = np.round(precision_score(y_test, y_pred, average='weighted'), 2)
end_time = time.time()
time_taken = np.round((end_time - start_time), 2)
temp_df.loc[len(temp_df)] = [dataset, dataform, X_train.shape[1], str(i).split('.')[-1][:-2], accuracy, f1, recall, precision, time_taken]
return temp_df

开始训练

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

lda = LinearDiscriminantAnalysis()
X_train_lda = lda.fit_transform(X_train, y_train)
X_test_lda = lda.transform(X_test)

预处理、分割和数据集的缩放，都与回归部分相同。在对8个不同的数据集进行新联后我们得到了下面结果:

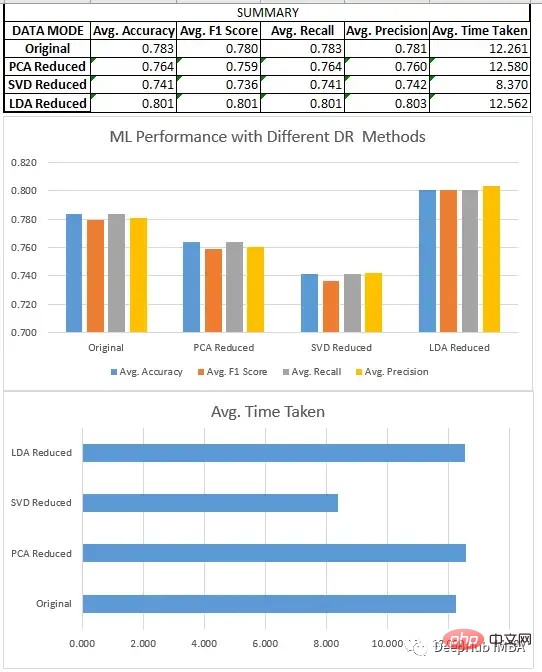
分类模型分析

我们比较了上面所有的三种方法SVD、LDA和PCA。

• LDA数据集通常优于原始形式的数据和由其他降维方法创建的低维数据，因为它旨在识别最有效区分类的特征的线性组合，而原始数据和其他无监督降维技术不关心数据集的标签。
• 降维技术在应用于更大的数据集时，可以极大地减少了数据集中的特征数量，这提高了机器学习模型的效率。在较小的数据集上，影响不是特别明显。除了LDA（它在这些情况下也很有效），因为它们在一些情况下，如二元分类，可以将数据集的维度减少到只有一个。
• 当我们在寻找一定的性能时，LDA可以是分类问题的一个非常好的起点。
• SVD与回归一样，模型的性能下降很明显。需要调整n_components的选择。

总结

我们比较了一些降维技术的性能，如奇异值分解(SVD)、主成分分析(PCA)和线性判别分析(LDA)。我们的研究结果表明，方法的选择取决于特定的数据集和手头的任务。

Bei Regressionsaufgaben stellen wir fest, dass PCA im Allgemeinen eine bessere Leistung erbringt als SVD. Bei der Klassifizierung übertrifft LDA SVD und PCA sowie den Originaldatensatz. Es ist wichtig, dass die lineare Diskriminanzanalyse (LDA) die Hauptkomponentenanalyse (PCA) bei Klassifizierungsaufgaben durchweg übertrifft, aber das bedeutet nicht, dass LDA generell eine bessere Technik ist. Dies liegt daran, dass es sich bei LDA um einen überwachten Lernalgorithmus handelt, der auf gekennzeichneten Daten basiert, um die diskriminierendsten Merkmale in den Daten zu lokalisieren, während es sich bei PCA um eine unbeaufsichtigte Technik handelt, die keine gekennzeichneten Daten erfordert und versucht, so viel Varianz wie möglich beizubehalten. Daher eignet sich PCA möglicherweise besser für unbeaufsichtigte Aufgaben oder Situationen, in denen die Interpretierbarkeit von entscheidender Bedeutung ist, während LDA möglicherweise besser für Aufgaben mit gekennzeichneten Daten geeignet ist.

Während Techniken zur Dimensionsreduktion dazu beitragen können, die Anzahl der Features in einem Datensatz zu reduzieren und die Effizienz von Modellen für maschinelles Lernen zu steigern, ist es wichtig, die möglichen Auswirkungen auf die Modellleistung und die Interpretierbarkeit der Ergebnisse zu berücksichtigen.

Der vollständige Code dieses Artikels:

https://github.com/salmankhi/DimensionalityReduction/blob/main/Notebook_25373.ipynb

Das obige ist der detaillierte Inhalt vonVergleich gängiger Technologien zur Dimensionsreduzierung: Machbarkeitsanalyse zur Reduzierung der Datendimensionen bei gleichzeitiger Wahrung der Informationsintegrität. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!