Quantitatives Modell des Parallelrechnens und seine Anwendung in Deep-Learning-Engines

Von den Kampfkünsten der Welt sind nur die schnellen unzerbrechlich. Die Frage, wie Deep-Learning-Modelle schneller trainiert werden können, steht seit jeher im Fokus der Branche. Branchenakteure entwickeln entweder spezielle Hardware oder entwickeln Software-Frameworks, die jeweils ihre einzigartigen Fähigkeiten unter Beweis stellen.

Natürlich sind diese Gesetze in Lehrbüchern und Literatur zur Computerarchitektur zu finden, wie zum Beispiel in diesem „Computerarchitektur: ein quantitativer Ansatz“, aber der Wert dieses Artikels liegt in seinem gezielten Ansatz. Wählen Sie die grundlegendsten Gesetze aus und kombinieren Sie sie mit einem Deep-Learning-Engine, um sie zu verstehen.

1 Annahmen zum Rechenumfang

Bevor wir das quantitative Modell des Parallelrechnens studieren, nehmen wir zunächst einige Einstellungen vor. Für eine bestimmte Trainingsaufgabe eines Deep-Learning-Modells kann unter der Annahme, dass die Gesamtberechnungsmenge V festgelegt ist, grob davon ausgegangen werden, dass das Deep-Learning-Modell das Training abschließt, solange die Berechnung der Größe von V abgeschlossen ist.

Diese GitHub-Seite (https://github.com/albanie/convnet-burden) listet den Berechnungsaufwand auf, den gängige CNN-Modelle zum Verarbeiten eines Bildes benötigen. Es ist zu beachten, dass auf dieser Seite der Berechnungsumfang aufgeführt ist In der Trainingsphase sind auch Berechnungen in der Rückwärtsphase erforderlich. Normalerweise ist die Anzahl der Berechnungen in der Rückwärtsphase größer als die Anzahl der Vorwärtsberechnungen. Dieses Papier (https://openreview.net/pdf?id=Bygq-H9eg) liefert ein intuitives Visualisierungsergebnis des Berechnungsumfangs der Verarbeitung eines Bildes in der Trainingsphase:

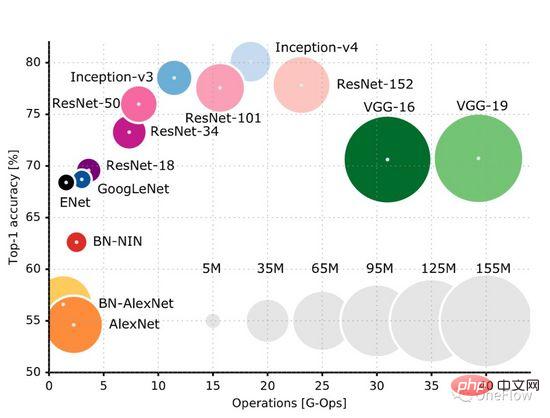
Nehmen Sie ResNet-50 als Beispiel. Die Trainingsphase erfordert 8G-Ops (ungefähr 8 Milliarden Berechnungen), um ein 224x224x3-Bild zu verarbeiten. Der gesamte ImageNet-Datensatz umfasst ungefähr 90 Mal (grobe Schätzung, Trainingsprozess). Insgesamt sind (8*10^9) *(1,2*10^6)* 90 = 0,864*10^18 Operationen erforderlich. Dann beträgt die Gesamtberechnungsmenge des ResNet-50-Trainingsprozesses ungefähr 1 Milliarde mal 1 Milliarde Operationen Wir können einfach davon ausgehen, dass die Modelloperation abgeschlossen ist, solange diese Berechnungen abgeschlossen sind. Das Ziel der Deep-Learning-Computing-Engine besteht darin, diese vorgegebene Berechnungsmenge in kürzester Zeit abzuschließen.

2 Annahmen zu Computergeräten

Dieser Artikel beschränkt sich auf das in der Abbildung unten gezeigte prozessorzentrierte Computergerät (Processor-Centric Computing), das in der Branche jedoch noch nicht untersucht wurde.

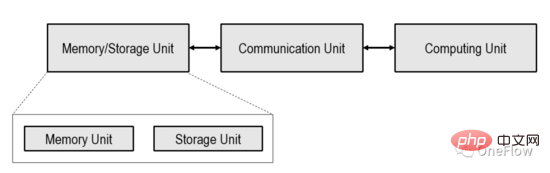
In dem in der Abbildung oben gezeigten Computergerät kann die Computereinheit ein Allzweckprozessor wie CPU, GPGPU oder ein Spezialchip wie TPU usw. sein. Wenn es sich bei der Recheneinheit um einen Allzweckchip handelt, werden Programme und Daten normalerweise in der Speichereinheit gespeichert, die heute auch der beliebteste Computer mit Von-Neumann-Struktur ist.

Wenn die Recheneinheit ein dedizierter Chip ist, werden normalerweise nur Daten in der Speichereinheit gespeichert. Die Kommunikationseinheit ist dafür verantwortlich, Daten von der Speichereinheit an die Recheneinheit zu übertragen und das Laden der Daten abzuschließen. Nachdem die Recheneinheit die Daten erhalten hat, ist sie für den Abschluss der Berechnung verantwortlich (die Daten werden dann von der Kommunikationseinheit übertragen). Die Berechnungsergebnisse werden in die Speichereinheit übertragen, um die Datenspeicherung abzuschließen.

Die Übertragungskapazität der Kommunikationseinheit wird normalerweise durch die Speicherzugriffsbandbreite Beta ausgedrückt, also die Anzahl der Bytes, die pro Sekunde übertragen werden können, die normalerweise mit der Anzahl der Kabel und der Frequenz des Signals zusammenhängt. Die Rechenleistung einer Recheneinheit wird in der Regel durch die Durchsatzrate pi dargestellt, die die Anzahl der Gleitkommaberechnungen (Flops) angibt, die pro Sekunde durchgeführt werden können. Dies hängt normalerweise mit der Anzahl der in die Recheneinheit integrierten logischen Rechengeräte zusammen Einheit und der Taktfrequenz.

Das Ziel der Deep-Learning-Engine besteht darin, die Datenverarbeitungsfähigkeiten des Computergeräts durch gemeinsames Software- und Hardware-Design zu maximieren, d. h. eine bestimmte Menge an Berechnungen in kürzester Zeit durchzuführen.

3 Roofline-Modell: Ein mathematisches Modell, das die tatsächliche Rechenleistung abbildet

Die tatsächliche Rechenleistung (Anzahl der pro Sekunde abgeschlossenen Vorgänge), die ein Computergerät bei der Ausführung einer Aufgabe erreichen kann, hängt nicht nur mit der Speicherzugriffsbandbreite Beta und dem zusammen theoretischer Spitzenwert pi der Recheneinheit Es hängt auch mit der arithmetischen Intensität (oder Betriebsintensität) der aktuellen Aufgabe selbst zusammen.

Die Rechenintensität einer Aufgabe ist definiert als die Anzahl der pro Byte Daten erforderlichen Gleitkommaberechnungen, also Flops pro Byte. Im Volksmund bedeutet eine Aufgabe mit geringer Rechenintensität, dass die Recheneinheit weniger Operationen an einem von der Kommunikationseinheit transportierten Byte durchführen muss. Um die Recheneinheit in diesem Fall beschäftigt zu halten, muss die Kommunikationseinheit häufig Daten transportieren Eine Aufgabe mit hoher Rechenintensität bedeutet, dass die Recheneinheit mehr Operationen an einem von der Kommunikationseinheit übertragenen Byte durchführen muss. Die Kommunikationseinheit muss nicht so häufig Daten übertragen, um die Recheneinheit zu beschäftigen.

Erstens darf die tatsächliche Rechenleistung den theoretischen Spitzen-Pi der Recheneinheit nicht überschreiten. Zweitens, wenn die Speicherzugriffsbandbreite Beta sehr klein ist, können in 1 Sekunde nur Beta-Bytes vom Speicher zur Recheneinheit übertragen werden. Stellen wir die Anzahl der Operationen dar, die für jedes Byte in der aktuellen Rechenaufgabe erforderlich sind, dann Beta * I stellt 1 Sekunde dar. Wenn Beta * I

Roofline-Modell ist ein mathematisches Modell, das auf der Grundlage der Beziehung zwischen der Speicherzugriffsbandbreite, der Spitzendurchsatzrate der Recheneinheit und der Rechenintensität der Aufgabe auf die tatsächliche Rechenleistung schließt. Es wurde 2008 von David Pattersons Team auf Communications of ACM veröffentlicht (https://en.wikipedia.org/wiki/Roofline_model) und ist ein einfaches und elegantes visuelles Modell:

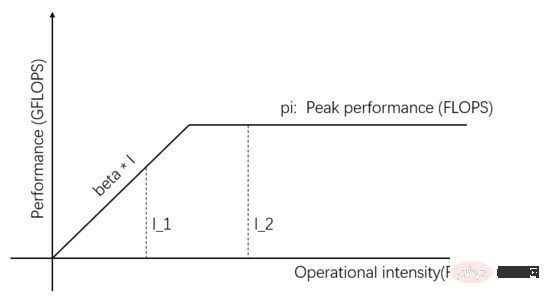
Abbildung 1: Dachlinienmodell

Das Unabhängige Variablen auf der horizontalen Achse von Abbildung 1 stellen die Rechenintensität verschiedener Aufgaben dar, d. h. die Anzahl der pro Byte erforderlichen Gleitkommaoperationen. Die abhängige Variable auf der vertikalen Achse stellt die tatsächlich erreichbare Rechenleistung dar, also die Anzahl der pro Sekunde durchgeführten Gleitkommaoperationen. Die obige Abbildung zeigt die tatsächliche Rechenleistung, die durch zwei Aufgaben mit der Rechenintensität I_1 und I_2 erreicht werden kann. Die Rechenintensität von I_1 ist kleiner als pi/beta, was als speicherzugriffsbegrenzte Aufgabe bezeichnet wird. Die tatsächliche Rechenleistung Beta * I_1 ist niedriger als der theoretische Peak pi.

Die Rechenintensität von I_2 ist höher als pi/beta, was als rechenbegrenzte Aufgabe bezeichnet wird. Die tatsächliche Rechenleistung erreicht den theoretischen Spitzenwert pi, und die Speicherzugriffsbandbreite nutzt nur pi/(I_2*beta). Die Steigung der Steigung in der Abbildung ist Beta. Der Schnittpunkt der Steigung und der theoretischen horizontalen Spitze pi wird als Gratpunkt bezeichnet. Die Abszisse des Gratpunkts ist gleich pi/beta pi/beta, die Kommunikationseinheit. Sie befindet sich in einem ausgeglichenen Zustand mit der Recheneinheit, und keines davon wird verschwendet.

Denken Sie daran, dass das Ziel der Deep-Learning-Engine darin besteht, „eine bestimmte Menge an Berechnungen in kürzester Zeit durchzuführen“, was darin besteht, die tatsächlich erreichbare Rechenleistung des Systems zu maximieren. Um dieses Ziel zu erreichen, stehen mehrere Strategien zur Verfügung.

I_2 in Abbildung 1 ist eine rechenbegrenzte Aufgabe. Die tatsächliche Rechenleistung kann verbessert werden, indem die Parallelität der Recheneinheit erhöht und dadurch der theoretische Spitzenwert erhöht wird, beispielsweise durch die Integration weiterer arithmetischer Logikeinheiten (ALU) in die Recheneinheit. Speziell für Deep-Learning-Szenarien bedeutet dies das Hinzufügen von GPUs, von einer GPU bis hin zu mehreren GPUs, die gleichzeitig arbeiten.

Wie in Abbildung 2 dargestellt, ist der theoretische Spitzenwert höher als Beta * I_2, wenn innerhalb der Recheneinheit mehr Parallelität hinzugefügt wird. Dann ist die tatsächliche Rechenleistung von I_2 höher und erfordert nur kürzere Zeit.

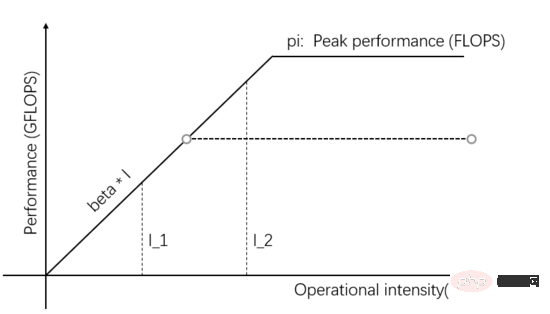
Abbildung 2: Erhöhen Sie den theoretischen Spitzenwert der Recheneinheit, um die tatsächliche Rechenleistung zu verbessern.

I_1 in Abbildung 1 ist eine speicherzugriffsbeschränkte Aufgabe. Sie können die tatsächliche Rechenleistung verbessern, indem Sie die Übertragungsbandbreite verbessern die Kommunikationseinheit. Verbessern Sie die Datenbereitstellungsmöglichkeiten. Wie in Abbildung 3 dargestellt, stellt die Steigung der Steigung die Übertragungsbandbreite der Kommunikationseinheit dar. Wenn die Steigung der Steigung zunimmt, ändert sich I_1 von einer speicherzugriffsbeschränkten Aufgabe zu einer berechnungsbeschränkten Aufgabe, und die tatsächliche Rechenleistung beträgt verbessert.

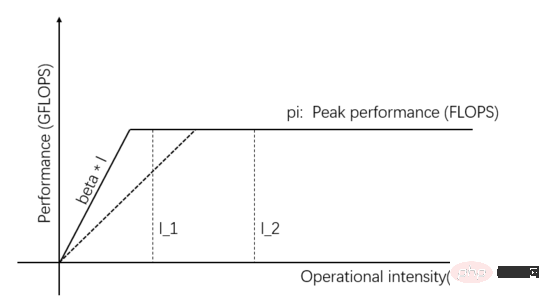
Abbildung 3: Verbesserung der Datenbereitstellungskapazität der Kommunikationseinheit zur Verbesserung der tatsächlichen Rechenleistung

Neben der Verbesserung der tatsächlichen Rechenleistung durch Verbesserung der Übertragungsbandbreite oder des theoretischen Spitzenwerts der Hardware kann diese auch verbessert werden durch Verbesserung der Rechenintensität der Aufgabe selbst. Tatsächliche Rechenleistung. Die gleiche Aufgabe kann auf viele verschiedene Arten implementiert werden, und auch die Rechenintensität verschiedener Implementierungen unterscheidet sich. Nachdem die Rechenintensität von I_1 auf mehr als pi/beta umgewandelt wurde, wird sie zu einer rechenbeschränkten Aufgabe, und die tatsächliche Rechenleistung erreicht pi und überschreitet das ursprüngliche Beta*I_1.

In tatsächlichen Deep-Learning-Engines werden alle die oben genannten drei Methoden (Erhöhung der Parallelität, Verbesserung der Übertragungsbandbreite und Verwendung von Algorithmen mit besserer Rechenintensität) verwendet.

4 Amdahls Gesetz: Wie berechnet man das Beschleunigungsverhältnis?

Das Beispiel in Abbildung 2 verbessert die tatsächliche Rechenleistung durch Erhöhung der Parallelität der Recheneinheit. Wie stark kann die Ausführungszeit der Aufgabe verkürzt werden? Hier geht es um das Beschleunigungsverhältnis, das heißt, der Wirkungsgrad wird um ein Vielfaches gesteigert.

Zur Vereinfachung der Diskussion gehen wir (1) davon aus, dass die aktuelle Aufgabe rechentechnisch begrenzt ist. Ich stelle die Rechenintensität dar, also I*beta>pi. Nachdem die Recheneinheit der Recheneinheit um das S-fache erhöht wurde, beträgt der theoretische Rechenspitzenwert s * pi. Nehmen Sie an, dass die Rechenintensität I der Aufgabe hoch genug ist, sodass sie nach dem Erhöhen des theoretischen Spitzenwerts um das S-fache unverändert bleibt rechnerisch begrenzt, das heißt I*beta > s*pi (2) Unter der Annahme, dass keine Pipeline verwendet wird, werden die Kommunikationseinheit und die Recheneinheit immer nacheinander ausgeführt (wir werden die Auswirkungen der Pipeline später speziell besprechen). Berechnen wir, wie oft sich die Effizienz der Aufgabenausführung verbessert hat.

In der Ausgangssituation, in der der theoretische Spitzenwert pi ist, überträgt die Kommunikationseinheit Betabytes an Daten in 1 Sekunde und die Recheneinheit benötigt (I*Beta)/pi Sekunden, um die Berechnung abzuschließen. Das heißt, wenn die Berechnung von I*beta innerhalb von 1+(I*beta)/pi Sekunden abgeschlossen ist, kann die Berechnung von (I*beta) / (1 + (I*beta)/pi) pro Einheit abgeschlossen werden Nehmen wir an, dass die Gesamtberechnungsmenge V beträgt, sodass insgesamt t1=V*(1+(I*beta)/pi)/(I*beta) Sekunden benötigt werden.

Nachdem die theoretische Berechnungsspitze durch Erhöhen der Parallelität um das S-fache erhöht wurde, benötigt die Kommunikationseinheit immer noch 1 Sekunde, um Betabytes an Daten zu übertragen, und die Recheneinheit benötigt (I*beta)/(s*pi) Sekunden, um den Vorgang abzuschließen Berechnung. Unter der Annahme, dass der Gesamtberechnungsaufwand V beträgt, dauert es t2=V*(1+(I*beta)/(s*pi))/(I*beta) Sekunden, um die Aufgabe abzuschließen.

Berechnen Sie t1/t2, um das Beschleunigungsverhältnis zu erhalten: 1/(pi/(pi+I*beta)+(I*beta)/(s*(pi+I*beta))). ist hässlich, liebe Leser. Sie können es selbst ableiten, es ist relativ einfach.

Wenn der theoretische Spitzenwert pi ist, dauert die Datenübertragung 1 Sekunde und die Berechnung (I*beta)/pi Sekunden. Dann beträgt das Verhältnis der Berechnungszeit (I*beta)/(pi + I*beta). Wir lassen p dieses Verhältnis darstellen, gleich (I*beta)/(pi + I*beta).

Wenn Sie p in das Beschleunigungsverhältnis von t1/t2 einsetzen, erhalten Sie das Beschleunigungsverhältnis als 1/(1-p+p/s). Dies ist das berühmte Amdahl-Gesetz (https://en.wikipedia.org/wiki). /Amdahl% 27s_law). Dabei stellt p den Anteil der ursprünglichen Aufgabe dar, der parallelisiert werden kann, s stellt das Vielfache der Parallelisierung dar und 1/(1-p+p/s) stellt die erzielte Beschleunigung dar.

Angenommen, die Kommunikationseinheit benötigt 1 Sekunde für die Datenübertragung und die Recheneinheit 9 Sekunden für die Berechnung, dann ist p=0,9. Nehmen wir an, wir verbessern die Parallelität der Recheneinheit und erhöhen ihren theoretischen Spitzenwert um das Dreifache, also s=3. Dann benötigt die Recheneinheit nur 3 Sekunden, um die Berechnung abzuschließen. Mithilfe des Amdahlschen Gesetzes können wir erkennen, dass das Beschleunigungsverhältnis das 2,5-fache beträgt und das Beschleunigungsverhältnis 2,5 kleiner ist als das Parallelitätsvielfache von 3 der Recheneinheit.

Wir haben den Reiz der Erhöhung der Parallelität der Recheneinheit gekostet. Können wir ein besseres Beschleunigungsverhältnis erzielen, indem wir die Parallelität weiter erhöhen? Dürfen. Wenn beispielsweise s = 9 ist, können wir ein 5-faches Beschleunigungsverhältnis erhalten und sehen, dass die Vorteile einer zunehmenden Parallelität immer kleiner werden.

Können wir das Beschleunigungsverhältnis erhöhen, indem wir s unendlich erhöhen? Ja, aber es wird immer weniger kosteneffektiv. Stellen Sie sich vor, wenn s gegen Unendlich geht (das heißt, wenn der theoretische Spitzenwert der Recheneinheit unendlich ist), tendiert p/s gegen 0, dann ist die maximale Beschleunigung Das Verhältnis beträgt 1/(1-p)=10.

Solange es im System einen nicht parallelisierbaren Teil (Kommunikationseinheit) gibt, darf das Beschleunigungsverhältnis 1/(1-p) nicht überschreiten.

Die tatsächliche Situation kann schlimmer sein als die Obergrenze des Beschleunigungsverhältnisses 1/(1-p), da in der obigen Analyse davon ausgegangen wird, dass die Rechenintensität I unendlich ist und bei Erhöhung der Parallelität der Recheneinheit die Übertragungsbandbreite von Die Kommunikationseinheit nimmt normalerweise ab. Dadurch wird p kleiner, sodass 1/(1-p) größer ist.

Diese Schlussfolgerung ist sehr pessimistisch. Selbst wenn der Kommunikationsaufwand (1-p) nur 0,01 beträgt, bedeutet dies, dass wir unabhängig von der Anzahl der Zehntausende paralleler Einheiten nur eine maximale Geschwindigkeitssteigerung von 100 erreichen können. Gibt es eine Möglichkeit, p so nah wie möglich an 1 zu bringen, d. h. 1-p nähert sich 0 und dadurch das Beschleunigungsverhältnis zu verbessern? Es gibt ein Wundermittel: das Fließband.

5 Pipelining: Allheilmittel

Bei der Ableitung des Amdahlschen Gesetzes gingen wir davon aus, dass die Kommunikationseinheit immer zuerst die Daten überträgt und dann die Recheneinheit berechnet abgeschlossen, die Kommunikationseinheit wird erneut auf die Daten übertragen und so weiter.

Können die Kommunikationseinheit und die Recheneinheit gleichzeitig arbeiten, Daten übertragen und gleichzeitig rechnen? Wenn die Recheneinheit nach der Berechnung jedes Datenelements sofort mit der Berechnung des nächsten Datenstapels beginnen kann, beträgt p nahezu 1. Unabhängig davon, wie oft der Parallelitätsgrad s erhöht wird, kann ein lineares Beschleunigungsverhältnis erhalten werden. Lassen Sie uns die Bedingungen untersuchen, unter denen eine lineare Beschleunigung erreicht werden kann.

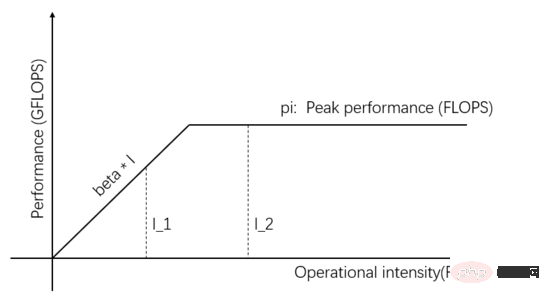
Abbildung 4: (Wie Abbildung 1) Roofline-Modell

I_1 in Abbildung 4 ist eine kommunikationsbeschränkte Aufgabe. Die Kommunikationseinheit kann Betabytes an Daten in 1 Sekunde transportieren, und die Recheneinheit muss diese verarbeiten Die Berechnungsmenge beträgt Beta*I_1 Operationen, die theoretische Berechnungsspitze beträgt Pi und es dauert insgesamt (Beta*I_1)/Pi Sekunden, um die Berechnung abzuschließen.

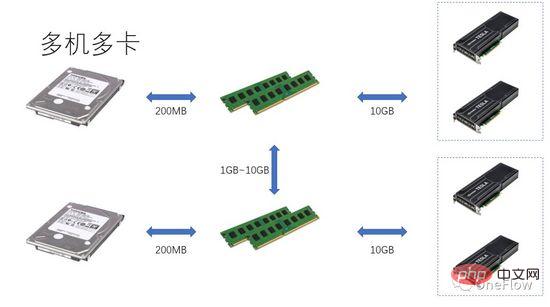
Für kommunikationsbeschränkte Aufgaben haben wir beta*I_1

I_2 in Abbildung 4 ist eine rechentechnisch begrenzte Aufgabe. Die Kommunikationseinheit kann Beta-Bytes an Daten in 1 Sekunde übertragen. Der Rechenaufwand, den die Recheneinheit benötigt, um diese Beta-Bytes zu verarbeiten, ist der theoretische Berechnungsspitzenwert ist pi. Es dauert insgesamt (beta*I_2)/pi Sekunden, um die Berechnung abzuschließen. Für rechenlimitierte Aufgaben gilt beta*I_2>pi, die Rechenzeit der Computing Unit ist also größer als 1 Sekunde.

Dies bedeutet auch, dass die Berechnung der Daten, die 1 Sekunde für die Übertragung benötigen, mehrere Sekunden dauert. Es bleibt genügend Zeit, um den nächsten Datenstapel innerhalb der Berechnungszeit zu übertragen, was bedeutet, dass die Berechnungszeit die Zeit verdecken kann Die Datenübertragungszeit beträgt maximal 1. Solange I unendlich ist, kann das Beschleunigungsverhältnis unendlich sein.

Die Technologie, die es der Kommunikationseinheit und der Recheneinheit ermöglicht, überlappend zu arbeiten, wird Pipelining genannt (Pipelining: https://en.wikipedia.org/wiki/Pipeline_(computing)). Es handelt sich um eine Technologie, die die Auslastung der Recheneinheit effektiv verbessert und das Beschleunigungsverhältnis verbessert.

6 Die Inspiration des quantitativen Modells des parallelen Rechnens für die Deep-Learning-Engine

Die verschiedenen oben diskutierten quantitativen Modelle sind auch auf die Entwicklung der Deep-Learning-Engine anwendbar. Beispielsweise kann sie für rechenbegrenzte Aufgaben beschleunigt werden Erhöhung des Parallelitätsgrads (Erhöhung der Grafikkarte); Auch wenn das gleiche Hardwaregerät verwendet wird, wirkt sich die Verwendung unterschiedlicher Parallelitätsmethoden (Datenparallelität, Modellparallelität oder Pipeline-Parallelität) auf die Rechenintensität aus Die verteilte Deep-Learning-Engine enthält einen großen Kommunikations-Overhead und Laufzeit-Overhead. Wie dieser Overhead reduziert oder maskiert werden kann, ist für den Beschleunigungseffekt von entscheidender Bedeutung.

Wenn Leser das auf GPU-Training basierende Deep-Learning-Modell aus der Perspektive eines prozessorzentrierten Computergeräts verstehen, können sie darüber nachdenken, wie sie eine Deep-Learning-Engine entwerfen können, um ein besseres Beschleunigungsverhältnis zu erzielen.

Bei einer einzelnen Maschine und einer einzelnen Karte müssen Sie nur die Datenübertragungs- und Berechnungspipeline abschließen, um eine 100-prozentige Auslastung der GPU zu erreichen. Die tatsächliche Rechenleistung hängt letztendlich von der Effizienz der zugrunde liegenden Matrixberechnung ab, also der Effizienz von cudnn. Theoretisch sollte es in einem Single-Card-Szenario keine Leistungslücke zwischen verschiedenen Deep-Learning-Frameworks geben.

Wenn Sie durch das Hinzufügen von GPUs innerhalb derselben Maschine eine Beschleunigung erzielen möchten, erhöht sich im Vergleich zum Einzelkartenszenario die Komplexität der Datenübertragung zwischen GPUs, und unterschiedliche Aufgabenteilungsmethoden können zu unterschiedlichen Rechenintensitäten führen Beispielsweise eignen sich Faltungsschichten für Datenparallelität und vollständig verbundene Schichten für Modellparallelität. Neben dem Kommunikationsaufwand wirkt sich auch der Laufzeitplanungsaufwand auf die Beschleunigung aus.

In Szenarien mit mehreren Maschinen und mehreren Karten wird die Komplexität der Datenübertragung zwischen GPUs weiter erhöht. Die Bandbreite der Datenübertragung zwischen Maschinen über das Netzwerk ist im Allgemeinen geringer als die Bandbreite der Datenübertragung über PCIe innerhalb der Maschine Dies bedeutet, dass der Grad der Parallelität erhöht, die Datenübertragungsbandbreite jedoch verringert wurde, was bedeutet, dass die Steigung im Roofline-Modell kleiner geworden ist. Szenarien wie CNN, die für Datenparallelität geeignet sind, bedeuten normalerweise hohe Rechenintensität I, und es gibt einige Modelle wie RNN/LSTM, bei denen die Rechenintensität I viel geringer ist, was auch bedeutet, dass der Kommunikationsaufwand in der Pipeline schwieriger zu vertuschen ist.

7 Zusammenfassung

Leser, die verteilte Deep-Learning-Engines verwendet haben, sollten eine persönliche Erfahrung mit dem Beschleunigungsverhältnis des Software-Frameworks haben. Grundsätzlich sind Faltungs-Neuronale Netze ein für Datenparallelität geeignetes Modell (mit relativ hoher Rechenintensität I). Durch Erhöhen verbessert Der Beschleunigungseffekt der GPU ist recht zufriedenstellend. Es gibt jedoch eine große Art von neuronalen Netzwerken, die Modellparallelität verwenden und eine höhere Rechenintensität aufweisen, und selbst wenn sie Modellparallelität verwenden, ist ihre Rechenintensität viel geringer Wie sich diese Anwendungen durch eine Erhöhung der GPU-Parallelität beschleunigen lassen, ist ein ungelöstes Problem in der Branche.

In früheren Deep-Learning-Bewertungen kam es sogar vor, dass die Verwendung mehrerer GPUs zum Trainieren von RNN langsamer war als eine einzelne GPU (https://rare-technologies.com/machine-learning-hardware-benchmarks/). Unabhängig davon, welche Technologie zur Lösung des Effizienzproblems der Deep-Learning-Engine eingesetzt wird, kommt es bei der Verbesserung des Beschleunigungsverhältnisses darauf an, den Laufzeitaufwand zu reduzieren, einen geeigneten Parallelmodus zur Erhöhung der Rechenintensität auszuwählen und zu maskieren Kommunikationsaufwand durch Pipelines im Rahmen der in diesem Artikel beschriebenen Grundgesetze.

Das obige ist der detaillierte Inhalt vonQuantitatives Modell des Parallelrechnens und seine Anwendung in Deep-Learning-Engines. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!