Erstellen Sie Ihre eigenen interaktiven Ereignisse – Bildschirmgestenerkennung

Dieser Artikel stammt von einem Mitglied des Byte Education-Adult and Innovation Front-end-Teams und wurde von ELab zur Veröffentlichung autorisiert.

TLDR

Dieser Artikel verwendet maschinelles Lernen, die Methode zur Bestimmung der Kosinusähnlichkeit und andere Methoden, um ein Schema zur Mausgestenerkennung zu entwerfen und zu überprüfen, und versucht, das Schema auf den dreidimensionalen Raum zu erweitern.

Hintergrund

Der Kerninhalt der Terminaltechnologie besteht darin, direkt auf Benutzerinteraktionen zu reagieren. Die Grundlogik besteht darin, dass es unter einer bestimmten Plattform einige vordefinierte Interaktionsereignisse gibt und die spezifischen Interaktionsaktionen des Benutzers die entsprechenden Interaktionsereignisse auslösen. Darauf basiert auch das gesamte User-Product-Interaction-Design. Um eine gute Benutzererfahrung zu erreichen, ist eine komfortable Interaktion erforderlich.

Im PC-Szenario ist die Maus (Trackpad) neben der Tastatur das wichtigste Eingabegerät, die Tasten und das Rad der Maus, daher sind die entsprechenden gemeinsamen Interaktionsereignisse Klicken, Scrollen und Ziehen. und diese Interaktionen erfordern ein Objekt (z. B. Klicken auf eine Schaltfläche, Scrollen eines Inhaltsbereichs oder des gesamten Ansichtsfensters, Ziehen eines Bilds), was nicht so praktisch ist wie Tastenkombinationen. In bestimmten Situationen sind Tastenkombinationen jedoch nicht so praktisch wie die Maus, sodass wir davon ausgehen, dass die Maus auch über Tastenkombinationen verfügt. Mausgesten sind eine relativ kleine, aber praktische und benutzerfreundliche Tastenkombination. Zu den gängigen Mausgesten gehören das Zeichnen gerader Linien, das Ankreuzen und das Zeichnen von Kreisen. In den frühen Tagen, als Hunderte von Browsern florierten, nutzten viele inländische Browser praktische Mausgestenbedienungen als Hauptverkaufsargument, um sich von der Konkurrenz abzuheben. Zu dieser Zeit erlangten Gestenbedienungen nach und nach breite Unterstützung und Anwendung und kultivierten den Markt stillschweigend. und Benutzergewohnheiten.

In mobilen Touchscreen-Szenarien liegen die Vorteile von Gestenoperationen auf der Hand. Gestenoperationen haben sich zum klassischen „Nach links wischen, um zurückzugehen“, „Nach rechts wischen, um vorwärts zu gehen“ und „Nach oben wischen, um zur Startseite zurückzukehren“ entwickelt. „Nach unten wischen, um Benachrichtigungen zu aktualisieren/aufzurufen/„Kontrollzentrum aktivieren“.

Mit dem jüngsten Aufstieg von VR/AR/MR wurden Gestenoperationen im dreidimensionalen Raum weiter gefördert und angewendet.

Daher nehmen wir die PC-Seite als Beispiel, um die Erkennung von Mausgesten zu realisieren, die Kernimplementierungslogik interaktiver Gesten zu klären und analog dazu zu versuchen, die Lösung auf weitere Terminalszenarien auszudehnen.

Ziel

• Kernlogikimplementierung: Aufnahme und Erkennung von Mausgesten realisieren. Für Mausgesten legen wir einige Voraussetzungen fest:

Schwenken und Zoomen werden nicht verformt, das heißt, die Gesamtposition und -größe des Gestenpfads ist nicht wichtig.

Es gibt eine gewisse Toleranz gegenüber wiederholten Gesten der Benutzer.

• Engineering-Kapselung: Konsolidieren Sie es zu einem benutzerdefinierten Ereignis, das über addEventListener überwacht werden kann, wodurch die Vielfalt der Interaktionen erweitert und der Entwicklungskomfort verbessert wird.
• Produktbasierte Erfahrung: Ermöglichen Sie Benutzern, ihre eigenen benutzerdefinierten Gesten hinzuzufügen.
• Lösungsdimensions-Upgrade: Erweitern Sie die aktuell erforschte Lösung auf den dreidimensionalen Raum.

Problemanalyse

Das Besondere an diesem Problem ist der Umgang mit Unsicherheit. Es besteht Unsicherheit in den vom Benutzer gezeichneten Mausgesten.

Für den Fall, dass ein Standardpfad voreingestellt ist, besteht das Problem darin, die Ähnlichkeit zwischen dem „voreingestellten deterministischen Pfad“ und dem „durch Benutzereingabe unsicheren Pfad“ zu erkennen.

Bei benutzerdefinierten Pfaden besteht das Problem darin, die Ähnlichkeit zwischen „dem vom Benutzer festgelegten Pfad der Unsicherheit“ und „dem vom Benutzer eingegebenen Pfad der Unsicherheit“ zu erkennen.

Wenn Sie dem traditionellen Programmiermodell folgen, müssen Sie eine strenge Programmlogik fordern, klare Regeln für bedingte Beurteilungen festlegen und diese Unsicherheit genau messen. Das heißt, es ist eine „magische Operation“ erforderlich. Durch Ersetzen der beiden Pfade können Sie feststellen, ob sie ähnlich sind.

Was die Geste selbst betrifft, können wir sie uns als gewöhnliches Rasterbild oder als Vektorgrafik vorstellen. Bei Rasterbildern können wir klassische Methoden des maschinellen Lernens verwenden, um die Klassifizierung des Bildes zu bestimmen, ohne den Inhalt des Bildes verstehen zu müssen. Für Vektorgrafiken müssen wir hierfür eine spezielle Datenstruktur definieren und uns mit der Darstellung der Ähnlichkeit von Grafiken befassen. Unsere nächste Implementierung wird von diesen beiden Ideen ausgehen.

Implementierungsplan

​Mit maschinellem Lernen​

Grundidee

Zunächst müssen Sie Ihre Denkweise ändern. Die Programmierung maschinellen Lernens unterscheidet sich grundlegend vom traditionellen Programmierdenken. Wie gerade erwähnt, erfordert die traditionelle Programmierung, dass Programmlogik wie bedingte Beurteilungen, Schleifen und andere Prozesse manuell genau spezifiziert und codiert werden müssen. Beim Programmieren für maschinelles Lernen geht es nicht mehr darum, detaillierte Logikregeln zu formulieren und zu schreiben, sondern es werden neuronale Netze aufgebaut, damit der Computer Funktionen erlernen kann.

Der Schlüssel zum maschinellen Lernen ist ein großer und zuverlässiger Datensatz. Um die Machbarkeit zu überprüfen, verwenden wir den ähnlichen handschriftlichen Zifferndatensatz mnist, um die reale Gestenszene zu ersetzen.

Also, unsere nächsten Schritte sind:

• Wählen Sie ein geeignetes Modell für maschinelles Lernen basierend auf den Merkmalen des Problems.
• Wählen Sie ein Framework für maschinelles Lernen basierend auf Benutzerfreundlichkeit.
• Trainieren Sie das Modell und holen Sie sich die Modelldatei.
• Stellen Sie das Modell bereit, führen Sie es aus und ziehen Sie Schlussfolgerungen.

Modellauswahl

Es gibt viele Algorithmen und Modelle für maschinelles Lernen, und sie müssen für verschiedene Bereiche ausgewählt werden. Tensorflow.js stellt offiziell eine Reihe vorab trainierter Modelle bereit [1], die direkt verwendet oder neu trainiert und verwendet werden können.

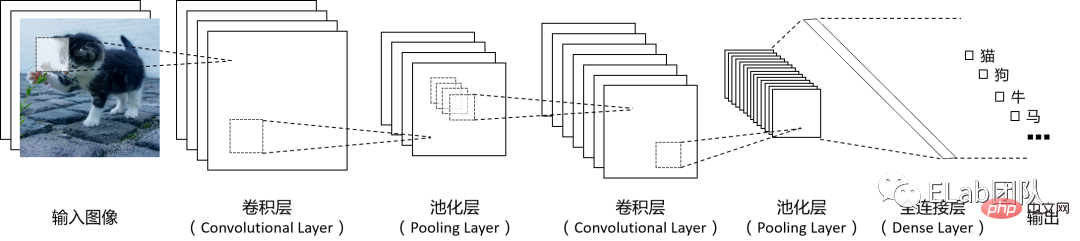
Convolutional Neural Networks CNN (Convolutional Neural Networks) ist ein sehr weit verbreitetes Modell für maschinelles Lernen, insbesondere bei der Verarbeitung von Bildern oder anderen Rasterfunktionen bei der Nutzung von Daten. Während der Informationsverarbeitung verwendet CNN die räumliche Struktur von Pixelzeilen und -spalten als Eingabe, extrahiert Merkmale über mehrere mathematische Berechnungsschichten, wandelt das Signal dann in einen Merkmalsvektor um und verbindet es nach der Merkmalsextraktion mit der Struktur eines herkömmlichen neuronalen Netzwerks , das Bild Der entsprechende Merkmalsvektor ist kleiner, wenn er dem herkömmlichen neuronalen Netzwerk bereitgestellt wird, und die Anzahl der zu trainierenden Parameter wird entsprechend reduziert. Das grundlegende Arbeitsprinzipdiagramm des Faltungs-Neuronalen Netzwerks lautet wie folgt (die Anzahl jeder Schicht im Diagramm kann nach Bedarf gestaltet werden):

Frame Auswahl

# 🎜🎜#Das Tensorflow.js-Framework ist aufgrund der folgenden Vorteile zu unserem bevorzugten Framework geworden:

Gute Portabilität: Tensorflow.js ist nicht das beliebteste und effizienteste Framework für maschinelles Lernen, aber aufgrund seiner Es basiert auf JS und verfügt über eine sofort einsatzbereite API, sodass es einfach auf verschiedenen Terminals ausgeführt und bereitgestellt werden kann, die JS unterstützen.

Geringe Latenz und hoher Datenschutz: Dank der Tatsache, dass es vollständig am Ende ausgeführt werden kann, ist es nicht erforderlich, Verifizierungsdaten an den Server zu senden und auf die Antwort des Servers zu warten, was die Vorteile bietet von geringer Latenz und hoher Sicherheit.

Geringe Lern-/Debugging-Kosten: Die Einstiegskosten für WEB-Entwickler sind gering, und der Browser kann den maschinellen Trainingsprozess gut visualisieren.

Die Umgebungseinrichtung von TFJS [2] ist sehr einfach und wird hier nicht erwähnt.

Modelltraining

Anhand dieses einfachen Beispiels können Sie die Idee der maschinellen Lernprogrammierung erleben und sich mit der API von Tensorflow.js vertraut machen. #🎜🎜 ## 🎜🎜 ## 🎜🎜#Dataset#🎜🎜 ## 🎜🎜#

 /** * @license* Copyright 2018 Google LLC. All Rights Reserved. * Licensed under the Apache License, Version 2.0 (the "License"); * you may not use this file except in compliance with the License. * You may obtain a copy of the License at * * http://www.apache.org/licenses/LICENSE-2.0 * * Unless required by applicable law or agreed to in writing, software * distributed under the License is distributed on an "AS IS" BASIS, * WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. * See the License for the specific language governing permissions and * limitations under the License. * ============================================================================= */ 
 const IMAGE_SIZE = 784;
 const NUM_CLASSES = 10;
 const NUM_DATASET_ELEMENTS = 65000;
 
 const NUM_TRAIN_ELEMENTS = 55000;
 const NUM_TEST_ELEMENTS = NUM_DATASET_ELEMENTS - NUM_TRAIN_ELEMENTS;
 
 const MNIST_IMAGES_SPRITE_PATH =
 'https://storage.googleapis.com/learnjs-data/model-builder/mnist_images.png';
 const MNIST_LABELS_PATH =
 'https://storage.googleapis.com/learnjs-data/model-builder/mnist_labels_uint8';
 
 /** * A class that fetches the sprited MNIST dataset and returns shuffled batches. * * NOTE: This will get much easier. For now, we do data fetching and * manipulation manually. */export class MnistData {
 constructor() {
 this.shuffledTrainIndex = 0;
 this.shuffledTestIndex = 0;
 }
 
 async load() {
 // Make a request for the MNIST sprited image.const img = new Image();
 const canvas = document.createElement('canvas');
 const ctx = canvas.getContext('2d');
 const imgRequest = new Promise((resolve, reject) => {
 img.crossOrigin = '';
 img.onload = () => {
 img.width = img.naturalWidth;
 img.height = img.naturalHeight;
 
 const datasetBytesBuffer =
 new ArrayBuffer(NUM_DATASET_ELEMENTS * IMAGE_SIZE * 4);
 
 const chunkSize = 5000;
 canvas.width = img.width;
 canvas.height = chunkSize;
 
 for (let i = 0; i < NUM_DATASET_ELEMENTS / chunkSize; i++) {
 const datasetBytesView = new Float32Array(
 datasetBytesBuffer, i * IMAGE_SIZE * chunkSize * 4,
 IMAGE_SIZE * chunkSize);
 ctx.drawImage(
 img, 0, i * chunkSize, img.width, chunkSize, 0, 0, img.width,
 chunkSize);
 
 const imageData = ctx.getImageData(0, 0, canvas.width, canvas.height);
 
 for (let j = 0; j < imageData.data.length / 4; j++) {
 // All channels hold an equal value since the image is grayscale, so// just read the red channel.datasetBytesView[j] = imageData.data[j * 4] / 255;
 }
 }
 this.datasetImages = new Float32Array(datasetBytesBuffer);
 
 resolve();
 };
 img.src = MNIST_IMAGES_SPRITE_PATH;
 });
 
 const labelsRequest = fetch(MNIST_LABELS_PATH);
 const [imgResponse, labelsResponse] =
 await Promise.all([imgRequest, labelsRequest]);
 
 this.datasetLabels = new Uint8Array(await labelsResponse.arrayBuffer());
 
 // Create shuffled indices into the train/test set for when we select a// random dataset element for training / validation.this.trainIndices = tf.util.createShuffledIndices(NUM_TRAIN_ELEMENTS);
 this.testIndices = tf.util.createShuffledIndices(NUM_TEST_ELEMENTS);
 
 // Slice the the images and labels into train and test sets.this.trainImages =
 this.datasetImages.slice(0, IMAGE_SIZE * NUM_TRAIN_ELEMENTS);
 this.testImages = this.datasetImages.slice(IMAGE_SIZE * NUM_TRAIN_ELEMENTS);
 this.trainLabels =
 this.datasetLabels.slice(0, NUM_CLASSES * NUM_TRAIN_ELEMENTS);
 this.testLabels =
 this.datasetLabels.slice(NUM_CLASSES * NUM_TRAIN_ELEMENTS);
 }
 
 nextTrainBatch(batchSize) {
 return this.nextBatch(
 batchSize, [this.trainImages, this.trainLabels], () => {
 this.shuffledTrainIndex =
 (this.shuffledTrainIndex + 1) % this.trainIndices.length;
 return this.trainIndices[this.shuffledTrainIndex];
 });
 }
 
 nextTestBatch(batchSize) {
 return this.nextBatch(batchSize, [this.testImages, this.testLabels], () => {
 this.shuffledTestIndex =
 (this.shuffledTestIndex + 1) % this.testIndices.length;
 return this.testIndices[this.shuffledTestIndex];
 });
 }
 
 nextBatch(batchSize, data, index) {
 const batchImagesArray = new Float32Array(batchSize * IMAGE_SIZE);
 const batchLabelsArray = new Uint8Array(batchSize * NUM_CLASSES);
 
 for (let i = 0; i < batchSize; i++) {
 const idx = index();
 
 const image =
 data[0].slice(idx * IMAGE_SIZE, idx * IMAGE_SIZE + IMAGE_SIZE);
 batchImagesArray.set(image, i * IMAGE_SIZE);
 
 const label =
 data[1].slice(idx * NUM_CLASSES, idx * NUM_CLASSES + NUM_CLASSES);
 batchLabelsArray.set(label, i * NUM_CLASSES);
 }
 
 const xs = tf.tensor2d(batchImagesArray, [batchSize, IMAGE_SIZE]);
 const labels = tf.tensor2d(batchLabelsArray, [batchSize, NUM_CLASSES]);
 
 return {xs, labels};
 }
 }

rreree

Modellbereitstellung und Auslauf

 // 我们直接使用mnist数据集这个经典的手写数字数据集，节约了收集手写数字的Erstellen Sie Ihre eigenen interaktiven Ereignisse – Bildschirmgestenerkennung集的时间
import {MnistData} from './data.js';

let cnnModel=null;

async function run() {
// 加载数据集 const data = new MnistData();
await data.load();
// 构造模型，设置模型参数 cnnModel = getModel();
// 训练模型 await train(cnnModel, data);
}

function getModel() {
const model = tf.sequential();

const IMAGE_WIDTH = 28;
const IMAGE_HEIGHT = 28;
const IMAGE_CHANNELS = 1;

// 在第一层，指定输入数据的形状，设置卷积参数 model.add(tf.layers.conv2d({
// 流入模型第一层的数据的形状。在本例中，我们的 MNIST 示例是 28x28 像素的黑白Erstellen Sie Ihre eigenen interaktiven Ereignisse – Bildschirmgestenerkennung。Erstellen Sie Ihre eigenen interaktiven Ereignisse – Bildschirmgestenerkennung数据的规范格式为 [row, column, depth] inputShape: [IMAGE_WIDTH, IMAGE_HEIGHT, IMAGE_CHANNELS],
// 要应用于输入数据的滑动卷积过滤器窗口的尺寸。在此示例中，我们将kernelSize设置成5，也就是指定 5x5 的卷积窗口。 kernelSize: 5,
// 尺寸为 kernelSize 的过滤器窗口数量 filters: 8,
// 滑动窗口的步长，即每次移动Erstellen Sie Ihre eigenen interaktiven Ereignisse – Bildschirmgestenerkennung时过滤器都会移动多少像素。我们指定步长为 1，表示过滤器将以 1 像素为步长在Erstellen Sie Ihre eigenen interaktiven Ereignisse – Bildschirmgestenerkennung上滑动。 strides: 1,
// 卷积完成后应用于数据的激活函数。在本例中，我们将应用修正线性单元 (ReLU) 函数，这是机器学习模型中非常常见的激活函数。 activation: 'relu',
// 通常使用 VarianceScaling作为随机初始化模型权重的方法 kernelInitializer: 'varianceScaling'
}));

// MaxPooling最大池化层使用区域最大值而不是平均值进行降采样 model.add(tf.layers.maxPooling2d({poolSize: [2, 2], strides: [2, 2]}));

// 重复一遍conv2d + maxPooling // 注意这次卷积的过滤器窗口数量更多 model.add(tf.layers.conv2d({
kernelSize: 5,
filters: 16,
strides: 1,
activation: 'relu',
kernelInitializer: 'varianceScaling'
}));
model.add(tf.layers.maxPooling2d({poolSize: [2, 2], strides: [2, 2]}));

// 现在我们将2维滤波器的输出展平为1维向量，作为最后一层的输入。这是将高维数据输入给最后的分类输出层时的常见做法。 // Erstellen Sie Ihre eigenen interaktiven Ereignisse – Bildschirmgestenerkennung是高维数据，而卷积运算往往会增大传入其中的数据的大小。在将数据传递到最终分类层之前，我们需要将数据展平为一个长数组。密集层（我们会用作最终层）只需要采用 tensor1d，因而此步骤在许多分类任务中很常见。 // 注意：展平层中没有权重。它只是将其输入展开为一个长数组。 model.add(tf.layers.flatten());

// 计算我们的最终概率分布，我们将使用密集层计算10个可能的类的概率分布，其中得分最高的类将是预测的数字。 const NUM_OUTPUT_CLASSES = 10;
model.add(tf.layers.dense({
units: NUM_OUTPUT_CLASSES,
kernelInitializer: 'varianceScaling',
activation: 'softmax'
}));

// 模型编译，选择优化器，损失函数categoricalCrossentropy，和精度指标accuracy（正确预测在所有预测中所占的百分比），然后编译并返回模型 const optimizer = tf.train.adam();
model.compile({
optimizer: optimizer,
loss: 'categoricalCrossentropy',
metrics: ['accuracy'],
});

return model;
}

// 我们的目标是训练一个模型，该模型会获取一张Erstellen Sie Ihre eigenen interaktiven Ereignisse – Bildschirmgestenerkennung，然后学习预测Erstellen Sie Ihre eigenen interaktiven Ereignisse – Bildschirmgestenerkennung可能所属的 10 个类中每个类的得分（数字 0-9）。 async function train(model, data) {
const metrics = ['loss', 'val_loss', 'acc', 'val_acc'];
const container = {
name: 'Model Training', tab: 'Model', styles: { height: '1000px' }
};
const fitCallbacks = tfvis.show.fitCallbacks(container, metrics);

const BATCH_SIZE = 512;
const TRAIN_DATA_SIZE = 5500;
const TEST_DATA_SIZE = 1000;

const [trainXs, trainYs] = tf.tidy(() => {
const d = data.nextTrainBatch(TRAIN_DATA_SIZE);
return [
d.xs.reshape([TRAIN_DATA_SIZE, 28, 28, 1]),
d.labels
];
});

const [testXs, testYs] = tf.tidy(() => {
const d = data.nextTestBatch(TEST_DATA_SIZE);
return [
d.xs.reshape([TEST_DATA_SIZE, 28, 28, 1]),
d.labels
];
});
// 设置特征和标签 return model.fit(trainXs, trainYs, {
batchSize: BATCH_SIZE,
validationData: [testXs, testYs],
epochs: 10, //训练轮次 shuffle: true,
callbacks: fitCallbacks
});
}

Programmevaluierung#🎜🎜 ## 🎜🎜#der Der Vorteil dieser Lösung besteht darin, dass der Vorhersageeffekt umso besser ist, je größer der am Training beteiligte Datensatz ist. Auch die Nachteile liegen auf der Hand. Erstens ist die Erstellung des Trainingsdatensatzes und des Verifizierungsdatensatzes ein enormer Arbeitsaufwand. Darüber hinaus ist das Training zwar während der Ausführung des Browsers möglich, aber dennoch zeitaufwändig. Zusammenfassend lässt sich sagen, dass diese Lösung mehrere vordefinierte Gesten erkennen kann, es jedoch schwierig ist, ein Modell zu trainieren, das die spezifischen Gesten des Benutzers anhand mehrerer Gesteneingaben des Benutzers erkennen kann. Weitere Fragen

Kann das OCR-Verfahren zur Handschrifterkennung zur Erkennung benutzerdefinierter Gesten genutzt werden?

Aufgrund der Unsicherheit der Benutzereingabe entsprechen die vom Benutzer eingegebenen Gesten nicht unbedingt einer bestimmten vordefinierten Kategorie. Kann die Bildklassifizierung die „andere“ Kategorie bestimmen?

Hängt das Format des Tensorflow-Modells mit der Framework-Sprache zusammen? Kann das von Python trainierte Modell beispielsweise weiterhin in tensorflow.js verwendet werden?

​Verwendung der geometrischen Analysemethode​

Grundidee

Was aus der Mausinteraktion erfasst wird, sind die Pfadinformationen, die wir erhalten kann extrahieren. Geben Sie spezifischere Informationen wie Standort, Form, Richtung usw. an. Daher können wir die Raum-Zeit-Trajektorie der Maus aufzeichnen und dann Regeln verwenden, um die Eigenschaften des Gestenpfads zusammenzufassen, sie zu einem Muster zu verfestigen, das die Geste mit hoher Wahrscheinlichkeit eindeutig identifizieren kann, und dann die Ähnlichkeit zwischen den Gesten zu vergleichen Gestenmuster und gewöhnliche Gesten. Beachten Sie, dass Sie beim Definieren der Pfaddatenstruktur berücksichtigen müssen, dass Größeneffekte und leichte Verformungen vermieden werden.

Extraktion und Aufzeichnung von Pfadmerkmalen

Zuerst muss der vom Benutzer gezeichnete Gestenpfad dargestellt werden. Wir klären ein Grundprinzip, dass Objekte mit derselben Form, aber unterschiedlichen Größen als dieselbe Geste betrachtet werden sollten. Der Gestenpfad muss durch eine Reihe von Einheitsvektoren dargestellt werden. In Stroke wird die Gestengrafik in 128 Vektoren unterteilt und jeder Vektor wird in einen Einheitsvektor umgewandelt. Selbst wenn die Größe und Länge der Gestenpfade unterschiedlich sind, sind die Daten, die sie darstellen, dieselben, solange sie strukturell gleich sind. Dadurch wird der Einfluss der Pfadgröße und einer leichten Verformung auf die Beurteilungsergebnisse eliminiert.

Darstellung der Pfadmerkmalsähnlichkeit

Dann wird die Ähnlichkeit des gemessenen Pfades in die Ähnlichkeit der gemessenen Vektordaten umgewandelt. Die Ähnlichkeit zwischen Pfaden wird durch den spezifischen Wert einer geometrischen Größe bestimmt. Daher haben wir die Kosinusähnlichkeit anhand der klassischen Methode zur Berechnung der Vektorähnlichkeit ermittelt.

向量的相似度通常使用余弦相似度来度量，即计算向量夹角的余弦值。将两组数据两两对应，分成128组向量，每组2个，计算每组向量的余弦值并累加。最终得到的结果应该会在 [-128, 128] 之间，数值越大也就表示相似度越高。我们只需设置一个阈值，超过这个阈值的就认为匹配成功。

为了计算两个向量夹角的余弦值，引入向量的点乘，根据向量点乘公式（推导过程[3]）：

这里|a|表示向量a的模（长度），θ表示两个向量之间的夹角。

两个互相垂直的向量的点积总是零。若向量a和b都是单位向量（长度为1），它们的点积就是它们的夹角的余弦。那么，给定两个向量，它们之间的夹角可以通过下列公式得到：

这个运算可以简单地理解为：在点积运算中，第一个向量投影到第二个向量上（这里，向量的顺序是不重要的，点积运算是可交换的），然后通过除以它们的标量长度来“标准化”。这样，这个分数一定是小于等于1的，可以简单地转化成一个角度值。

对于二维向量，我们用一个[number, number]元组来表示。

核心实现逻辑：

import { useEffect, useState, useRef, useMemo } from 'react'
import throttle from "lodash/throttle"

type Position = {x:number, y:number};
type Vector = [number, number];

// 预先定义特殊V字型的手势路径，便于调试。 const shapeVectors_v: Vector[] = [[5,16],[13,29],[4,9],[6,9],[8,8],[1,0],[1,0],[1,-2],[0,-3],[7,-11],[21,-34],[10,-19]];
const shapeVectors_l: Vector[] = [[0,15],[0,33],[0,19],[0,4],[0,3],[0,8],[2,6],[11,0],[28,0],[18,0],[5,0],[1,0]]
const shapeVectors_6: Vector[] = [[-41,18],[-40,33],[-30,39],[-24,62],[1,53],[40,27],[38,2],[30,-34],[7,-41],[-31,-21],[-38,-4],[-19,0]];
const shapeVectors: {[key:string]: Vector[]} = {
v: shapeVectors_v,
l: shapeVectors_l,
6: shapeVectors_6
}

function Gesture(){
const pointsRef = useRef<Position[]>([]);
const sparsedPointsRef = useRef<Position[]>([]);
const vectorsRef = useRef<Vector[]>([]);

const canvasContextRef = useRef<CanvasRenderingContext2D>()
const containerRef = useRef<HTMLDivElement>(null)

const [predictResults, setPredictResults] = useState<{label: string, similarity: number}[]>([])

// 按一定的时间间隔采集点 const handleMouseMoveThrottled = useMemo(()=>{return throttle(handleMouseMove, 16)}, [canvasContextRef.current])

useEffect(()=>{
const canvasEle = document.getElementById('canvas-ele') as HTMLCanvasElement;
const ctx = canvasEle.getContext('2d')!;
canvasContextRef.current=ctx;
handleClear();
}, [])

function handleMouseDown(){
containerRef?.current?.addEventListener('mousemove', handleMouseMoveThrottled);
}

function handleMouseUp(){
console.log('up')
containerRef?.current?.removeEventListener('mousemove', handleMouseMoveThrottled);
console.log('points', sparsedPointsRef.current)
console.log('vectors', JSON.stringify(vectorsRef.current))
pointsRef.current=[]
}

// 为了方便示意，我们把鼠标路径可视化出来。 function drawPoint(x:number,y:number){
// console.log(x, y) // canvasContext?.arc(x, y, 5, 0, Math.PI*2); (canvasContextRef.current!).fillStyle = 'red';
canvasContextRef.current?.fillRect(x, y, 10,10)
}

// 鼠标滑过时，记录下一串间隔的点。 function handleMouseMove(e: any){
const x:number = e.offsetX, y:number = e.offsetY;
drawPoint(x, y)
const newPoints = [...pointsRef.current, {x,y}];
pointsRef.current = newPoints;
const sparsedNewPoints = sparsePoints(newPoints);
sparsedPointsRef.current=sparsedNewPoints;
const vectors = points2Vectors(sparsedNewPoints)
vectorsRef.current = vectors;
console.log('points', x, y)
// const angles = vectors.map(vector2PolarAngle) // console.log('angles', angles[angles.length-1]) }

// 如果点太多，处理起来性能不佳，除了节流之外，我们始终将点抽稀到13个（我们假设每个手势的持续时间都不低于200ms，能保证在节流16ms的情况下，至少收集到13个原始点，这样抽稀才有意义） // 抽稀的策略是以固定的间隔平均抽，这样有个潜在问题：如果用户划手势时速度不够均匀，比如在同一个手势路径中某段时间划的速度比较快（点会比较密集），在某段时间的速度比较慢（点会比较稀疏），那由抽稀后的点构造出的路径向量就会比较失真，影响最终判断的准确性。 // 优化的方案是在空间上采用分区抽稀的策略，避免用户手速不均匀导致的问题，但分区逻辑比较复杂，我们暂且按下不做深入研究。 // todo: 抽稀后，相邻的点不能重复，否则会有0向量、对运算和判断造成干扰。 function sparsePoints(points: Position[]){
const sparsedLength = 13;
if(points.length<=sparsedLength){
return points;
}else{
let sparsedPoints = [];
let step = points.length/sparsedLength;
for(let i=0; i<sparsedLength; i++){
const curIndex = Math.round(step*i);
sparsedPoints.push(points[curIndex])
}
return sparsedPoints;
}
}

// 对于非闭合的路径，手势方向会影响判断逻辑，相同的路径可能是由相反的手势方向画出来的。比如L形的手势。 // 对于闭合的路径，手势的方向和起止位置都会影响判断逻辑，相同的路径可能是由相反的手势方向画出来的，也可能是由不同起始位置画出来的。比如圆形的手势。 // 为了消除相同路径不同画法的影响，我们做如下处理 
function normalizePoints(points:Position[]){
// if (是闭合路径) 将位置在最左上角的点作为数组的第一位，其余的依次排列，然后返回 // else 原样返回 return points;
}

// 相邻的两个点相连，生成一个向量。用这n个点的坐标生成n-1个向量，这n-1个向量组成一段路径，用来表示一个鼠标手势。 function points2Vectors(points: Position[]){
if(points.length<=1){
return []
}else{
return points.reduce((pre:Vector[], cur, curIdx)=>{
if(curIdx===0){return []}
const prePoint = points[curIdx-1];
const vec:Vector = [cur.x-prePoint.x, cur.y-prePoint.y];
return [...pre, vec];
}, [])
}
}

// 判断两条路径是否是相同，保证组成两条路径的向量数相同，然后计算两条路径对应向量的余弦相似度（取值在-1~1之间，越接近-1或者1，越相似）。最后再与定义的阈值比较，超过阈值就认为路径相同。 function judge(vec1:Vector[], vec2: Vector[], threshold?:number){
// 暂定阈值为0.5 const finalThreshold = threshold||0.5;
// 为消除路径方向的影响（一个向量与另一个反向相反的向量的余弦值是-1，应该认为它们形状相同），反转路径后再次判断 return cosineSimilarity(vec1, vec2)>=finalThreshold || cosineSimilarity(vec1, vec2.reverse())>=finalThreshold
}

// 两组向量的余弦相似度，保证组成两条路径的向量数相同，然后计算两条路径对应向量的余弦值，累加取均值.取值在-1~1之间，越接近-1或者1，越相似. function cosineSimilarity(vec1: Vector[], vec2: Vector[]){
if(vec1.length!==vec2.length){
console.warn('进行比较的两个路径长度（路径内的向量数）必须一致')
return 0;
}else{
let cosValueSum = 0;
vec1.forEach((v1, i)=>{
cosValueSum+=vectorsCos(v1, vec2[i])
})
// 取余弦值的绝对值，绝对值越接近1，相似度越高。 const cosValueRate = Math.abs(cosValueSum/vec1.length);
console.log('cosValueRate', cosValueRate)
return cosValueRate;
}
}

// 两个向量的余弦值 function vectorsCos(v1:Vector, v2:Vector){
// 特殊情况，0向量的余弦值我们认为是1 if(vectorLength(v1)*vectorLength(v2)===0){
return 1;
}
return vectorsDotProduct(v1, v2)/(vectorLength(v1)*vectorLength(v2));
}

// 向量的点乘 function vectorsDotProduct(v1:Vector, v2:Vector){
return v1[0]*v2[0]+v1[1]*v2[1];
}
// 向量的长度 function vectorLength(v:Vector){
return Math.sqrt(Math.pow(v[0], 2)+Math.pow(v[1], 2))
}

// 向量归一化，消除向量在长度上的差异，控制变量，方便训练机器学习模型(https://zhuanlan.zhihu.com/p/424518359) function normalizeVector(vec:Vector){
const length = Math.sqrt(Math.pow(vec[0],2)+Math.pow(vec[1], 2))
return [vec[0]/length, vec[1]/length]
}

function handlePredict(){
const results = Object.keys(shapeVectors).map(key=>({
label: key,
similarity: cosineSimilarity(shapeVectors[key], vectorsRef.current),
}))
setPredictResults(results);
console.log('results', results)
}

function handleClear(){
pointsRef.current=[];
sparsedPointsRef.current=[];
vectorsRef.current=[];
(canvasContextRef.current!).fillStyle = 'rgb(0,0,0)';
(canvasContextRef.current!).fillRect(0, 0, 500, 500);
setPredictResults([]);
}

// 工程化封装，为某个dom元素增加自定义手势事件 function addCustomEvent(ele: HTMLElement, eventName: string, eventLisener:(...args:any[])=>any){
let points = [], sparsedPoints=[],vecs:Vector[]=[];
const customEvent = new Event(eventName);

function handleMouseMove(e: any){
const x:number = e.offsetX, y:number = e.offsetY;
const newPoints = [...pointsRef.current, {x,y}];
points = newPoints;
const sparsedNewPoints = sparsePoints(newPoints);
sparsedPoints=sparsedNewPoints;
const newVectors = points2Vectors(sparsedNewPoints)
vecs = newVectors;
console.log('points', x, y)
}

const handleMouseMoveThrottled = throttle(handleMouseMove, 16)

function handleMouseDown(){
ele.addEventListener('mousemove', handleMouseMoveThrottled);
}

function handleMouseUp(){
console.log('up')
ele.removeEventListener('mousemove', handleMouseMoveThrottled);
console.log('points', sparsedPointsRef.current)
console.log('vectors', JSON.stringify(vectorsRef.current))
if(judge(vecs, shapeVectors['l'], 0.6)){
ele.dispatchEvent(customEvent)
}
points=[], sparsedPoints=[], vecs=[];
}

ele.addEventListener(eventName, eventLisener)
ele.addEventListener('mousedown', handleMouseDown);
ele.addEventListener('mouseup', handleMouseUp);

return function distroyEventListener(){
ele.removeEventListener(eventName, eventLisener)
}
}

return 
<canvas  width='500' height="500"></canvas>
<section>
<button notallow={handlePredict}>预测</button>
<button notallow={handleClear}>清空</button>
</section>
<ul>
{predictResults.map(e=>(
<li key={e.label}>
{`与 ${e.label}的相似度：${e.similarity}`}
</li>
))}
</ul>

}
export default Gesture

性能优化

点和向量的计算属于计算密集型任务，且其需要与主线程通信的数据量不大，考虑将其搬进webworker。此外，canvas的渲染性能也可以使用requestAnimationFrame和硬件加速来优化。属于常见的工程层面优化，此处略。

方案评价

余弦相似度的方法，优势在于计算量不大，可以在运行时由用户自定义手势，且所需保存的数据量不大，也适合网络传输。劣势在于难以衡量复杂多笔画、没有严格笔顺的图形的相似度。

​扩展到三维空间​

针对二维平面内的手势识别方案如何扩展到三维空间呢？比如在VR/MR场景内，手势路径会是一组三维向量，如果我们能将余弦相似度的适用范围扩展到三维向量，也就顺理成章地解决了这个问题。

基本思路就是分别分析两个三维向量在xoy平面上的投影之间的夹角以及在yoz平面上的投影之间的夹角的余弦相似度，将两者的乘积作为两个三维向量之间的余弦相似度。判断逻辑与二维向量的一致。

​综合方案​

综合考虑机器学习的方案和几何分析方案的优劣势，我们做如下设计。对于预设的手势，我们构造数据集、离线训练模型，然后将模型内置在产品内。对于自定义的手势，我们采用几何分析方案，让用户连续输入3次，先计算每次输入的路径的两两之间的相似度，且选出相似度的最小值n，如果最小值n大于某个阈值m，且每次输入的路径与其他已有路径的相似度均小于m时，我们就将距离其余两条路径的相似度之和最小的那条路径作为用户自定义的新路径，n作为其相似度判断的阈值。

参考资料

[1]预训练好的模型: https://github.com/tensorflow/tfjs-models

[2]环境搭建: https://github.com/tensorflow/tfjs#getting-started

[3]推导过程: https://blog.csdn.net/dcrmg/article/details/52416832

[4]复杂鼠标手势的识别是如何实现的? - 知乎: https://www.zhihu.com/question/20607813

[5]点积相似度、余弦相似度、欧几里得相似度: https://zhuanlan.zhihu.com/p/159244903

[6]机器学习并没有那么深奥，它还很有趣（1）-36氪: https://m.36kr.com/p/1721248956417

[7]计算向量间相似度的常用方法: https://cloud.tencent.com/developer/article/1668762

[8]C#手势库的核心逻辑实现: https://github.com/poerin/Stroke/blob/master/Stroke/Gesture.cs

[9]什么是张量 (tensor)? - 知乎: https://www.zhihu.com/question/20695804

[10]使用 CNN 识别手写数字: https://codelabs.developers.google.com/codelabs/tfjs-training-classfication?hl=zh-cn#0

[11]机器学习: https://zh.m.wikipedia.org/zh/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0

[12]文字识别方法整理（2015~2019）: https://zhuanlan.zhihu.com/p/65707543

Das obige ist der detaillierte Inhalt vonErstellen Sie Ihre eigenen interaktiven Ereignisse – Bildschirmgestenerkennung. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!