Schrittweise Visualisierung des Entscheidungsprozesses des Gradient-Boosting-Algorithmus

Der Gradient-Boosting-Algorithmus ist eine der am häufigsten verwendeten Ensemble-Techniken für maschinelles Lernen. Dieses Modell verwendet eine Folge schwacher Entscheidungsbäume, um einen starken Lernenden aufzubauen. Dies ist auch die theoretische Grundlage der Modelle XGBoost und LightGBM. Daher werden wir in diesem Artikel ein Gradient-Boosting-Modell von Grund auf erstellen und es visualisieren.

Einführung in den Gradient Boosting-Algorithmus

Der Gradient Boosting-Algorithmus (Gradient Boosting) ist ein Ensemble-Lernalgorithmus, der die Vorhersagegenauigkeit des Modells verbessert, indem er mehrere schwache Klassifikatoren erstellt und diese dann zu einem starken Klassifikator kombiniert.

Das Prinzip des Gradient-Boosting-Algorithmus kann in die folgenden Schritte unterteilt werden:

1. Initialisierung des Modells: Im Allgemeinen können wir ein einfaches Modell (z. B. einen Entscheidungsbaum) als anfänglichen Klassifikator verwenden.
2. Berechnen Sie den negativen Gradienten der Verlustfunktion: Berechnen Sie den negativen Gradienten der Verlustfunktion unter dem aktuellen Modell für jeden Abtastpunkt. Dies entspricht der Aufforderung an den neuen Klassifikator, den Fehler unter das aktuelle Modell anzupassen.
3. Trainieren Sie einen neuen Klassifikator: Verwenden Sie diese negativen Gradienten als Zielvariablen, um einen neuen schwachen Klassifikator zu trainieren. Dieser schwache Klassifikator kann ein beliebiger Klassifikator sein, z. B. ein Entscheidungsbaum, ein lineares Modell usw.
4. Modell aktualisieren: Fügen Sie dem Originalmodell neue Klassifikatoren hinzu und kombinieren Sie sie mithilfe des gewichteten Durchschnitts oder anderer Methoden.
5. Iteration wiederholen: Wiederholen Sie die obigen Schritte, bis die voreingestellte Anzahl von Iterationen erreicht ist oder die voreingestellte Genauigkeit erreicht ist.

Da der Gradient-Boosting-Algorithmus ein serieller Algorithmus ist, ist seine Trainingsgeschwindigkeit möglicherweise langsamer. Lassen Sie uns ihn anhand eines praktischen Beispiels vorstellen:

Angenommen, wir haben einen Funktionssatz Xi und einen Wert Yi und möchten y als beste Schätzung berechnen

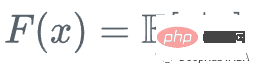
Wir beginnen mit dem Mittelwert von y

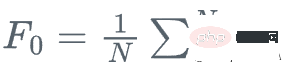
Bei jedem Schritt möchten wir, dass F_m(x) näher an y|x liegt.

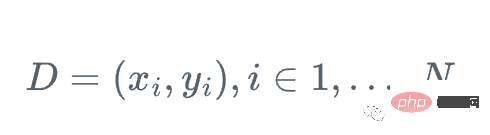
Bei jedem Schritt möchten wir, dass F_m(x) eine bessere Näherung für y bei gegebenem x ist.

Zuerst definieren wir eine Verlustfunktion

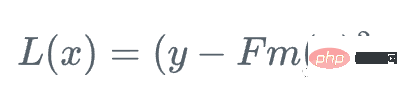
Dann gehen wir in die Richtung, in der die Verlustfunktion in Bezug auf die Fm des Lernenden am schnellsten abnimmt:

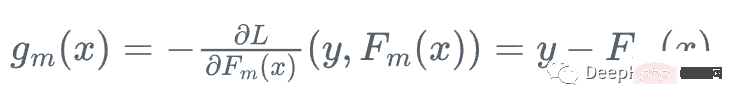
, weil wir y nicht berechnen können für jedes x , daher ist der genaue Wert dieses Gradienten nicht bekannt, aber für jedes x_i in den Trainingsdaten ist der Gradient genau gleich dem Rest von Schritt m: r_i!

Wir können also einen schwachen Regressionsbaum h_m verwenden Approximieren Sie die Gradientenfunktion g_m für das Residuum. Führen Sie das Training durch:

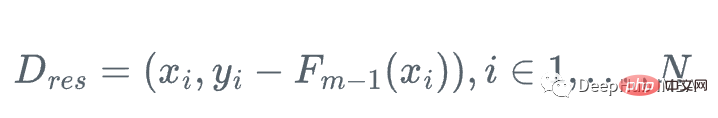
Dann aktualisieren wir den Lernenden

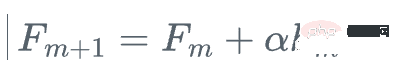
Dies ist eine Gradientenverstärkung, anstatt den wahren Gradienten g_m der Verlustfunktion relativ zu zu verwenden Der aktuelle Lernende aktualisiert den aktuellen Lernenden F_{m} und verwendet stattdessen den schwachen Regressionsbaum h_m, um ihn zu aktualisieren.

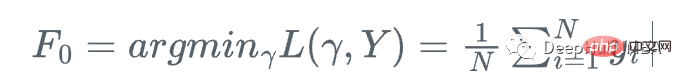
Das heißt, die folgenden Schritte wiederholen:

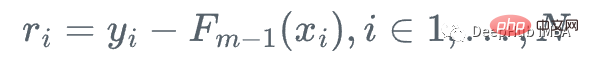2. Passen Sie den Regressionsbaum h_m an die Trainingsstichprobe und ihr Residuum an

3 Schrittgrößen-Alpha-Update-Modell

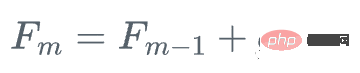sieht kompliziert aus, oder? Visualisieren wir den Prozess und es wird sehr klar werden

Visualisierung des Entscheidungsprozesses

Hier verwenden wir den Monddatensatz von sklearn, weil dies ein Klassische nichtlineare kategoriale Daten

import numpy as np
 import sklearn.datasets as ds
 import pandas as pd
 import matplotlib.pyplot as plt
 import matplotlib as mpl
 
 from sklearn import tree
 from itertools import product,islice
 import seaborn as snsmoonDS = ds.make_moons(200, noise = 0.15, random_state=16)
 moon = moonDS[0]
 color = -1*(moonDS[1]*2-1)
 
 df =pd.DataFrame(moon, columns = ['x','y'])
 df['z'] = color
 df['f0'] =df.y.mean()
 df['r0'] = df['z'] - df['f0']
 df.head(10)

Visualisieren wir die Daten:

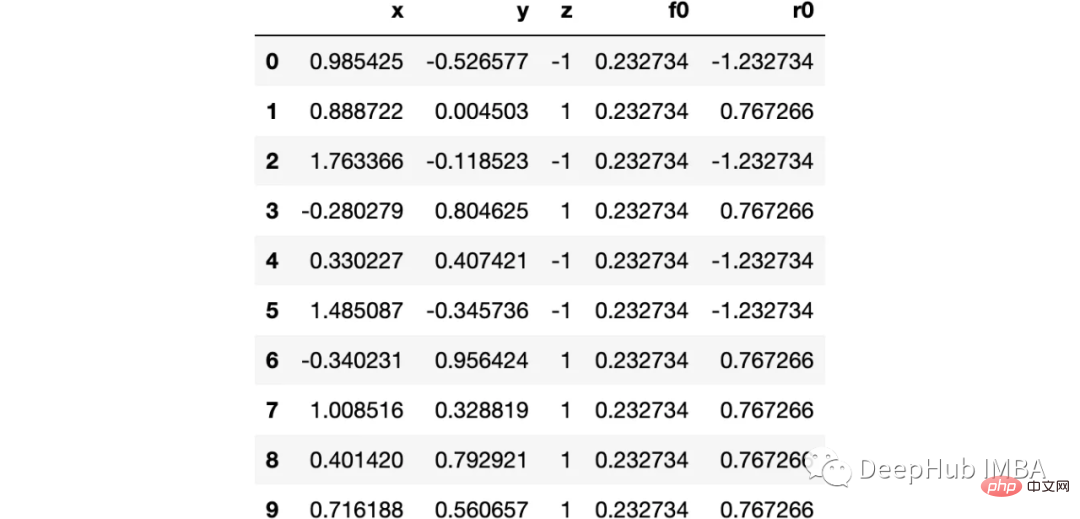
下图可以看到，该数据集是可以明显的区分出分类的边界的，但是因为他是非线性的，所以使用线性算法进行分类时会遇到很大的困难。

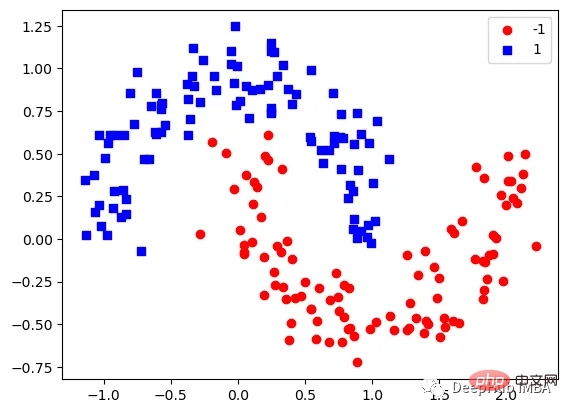
那么我们先编写一个简单的梯度增强模型:

def makeiteration(i:int):
"""Takes the dataframe ith f_i and r_i and approximated r_i from the features, then computes f_i+1 and r_i+1"""
clf = tree.DecisionTreeRegressor(max_depth=1)
clf.fit(X=df[['x','y']].values, y = df[f'r{i-1}'])
df[f'r{i-1}hat'] = clf.predict(df[['x','y']].values)
 
eta = 0.9
df[f'f{i}'] = df[f'f{i-1}'] + eta*df[f'r{i-1}hat']
df[f'r{i}'] = df['z'] - df[f'f{i}']
rmse = (df[f'r{i}']**2).sum()
clfs.append(clf)
rmses.append(rmse)

上面代码执行3个简单步骤:

将决策树与残差进行拟合:

clf.fit(X=df[['x','y']].values, y = df[f'r{i-1}'])
 df[f'r{i-1}hat'] = clf.predict(df[['x','y']].values)

然后，我们将这个近似的梯度与之前的学习器相加:

df[f'f{i}'] = df[f'f{i-1}'] + eta*df[f'r{i-1}hat']

最后重新计算残差:

df[f'r{i}'] = df['z'] - df[f'f{i}']

步骤就是这样简单，下面我们来一步一步执行这个过程。

第1次决策

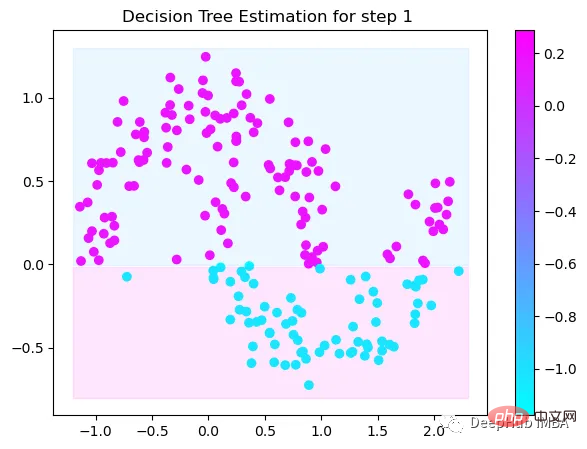
Tree Split for 0 and level 1.563690960407257

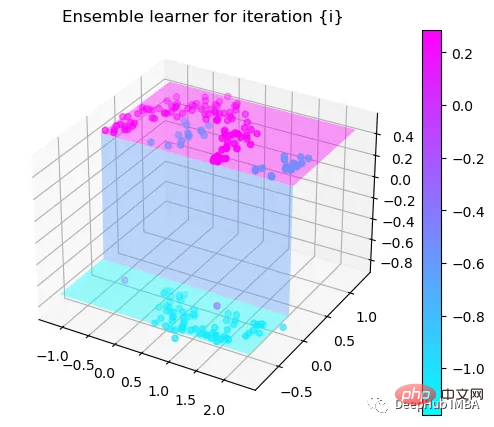
第2次决策

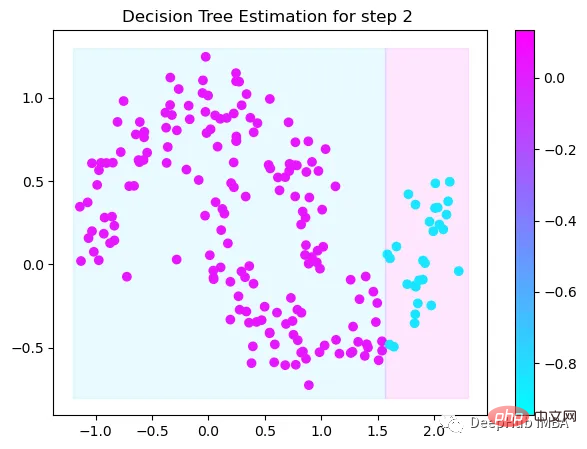
Tree Split for 1 and level 0.5143677890300751

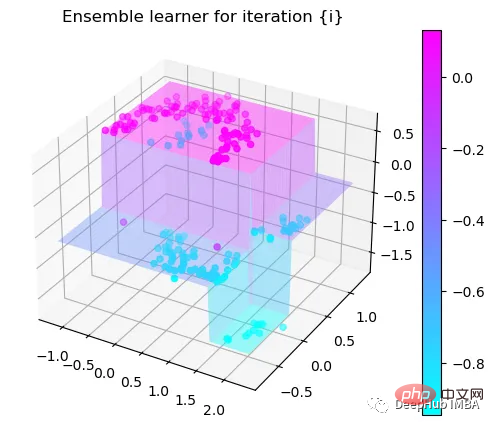
第3次决策

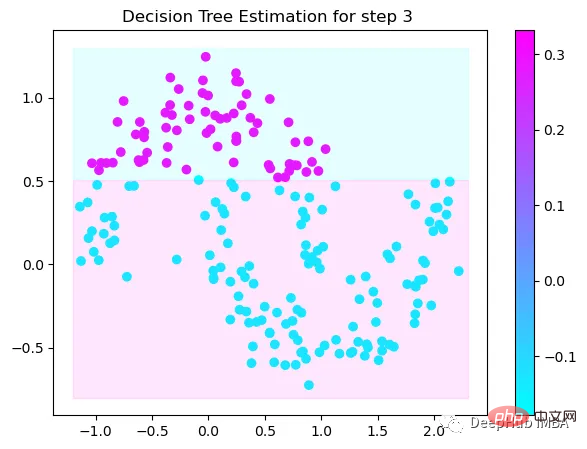
Tree Split for 0 and level -0.6523728966712952

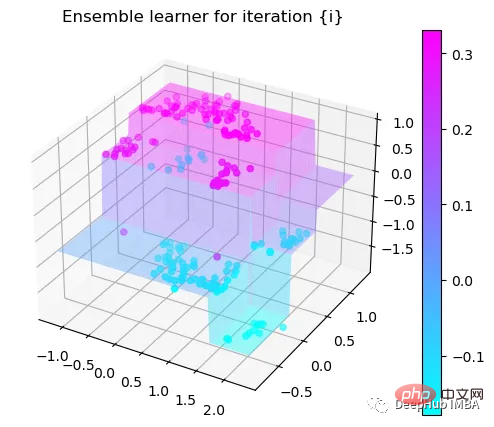
第4次决策

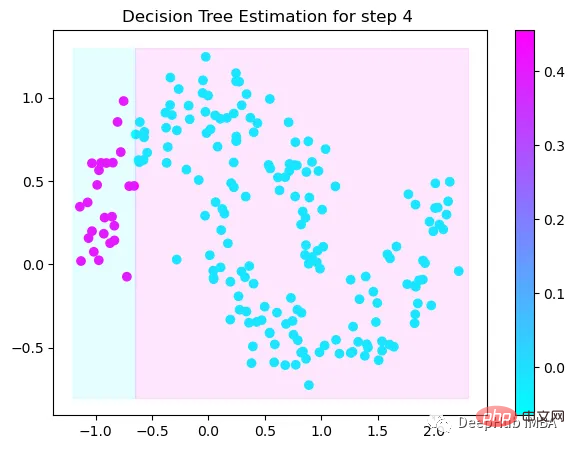
Tree Split for 0 and level 0.3370491564273834

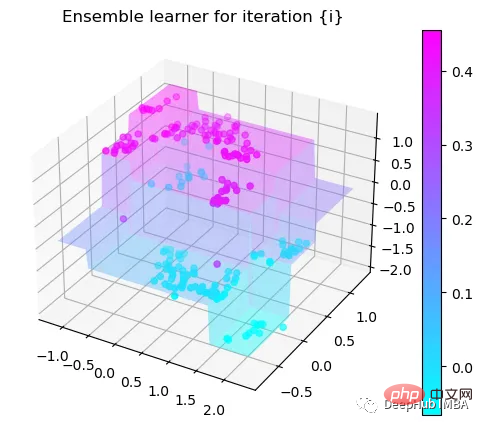
第5次决策

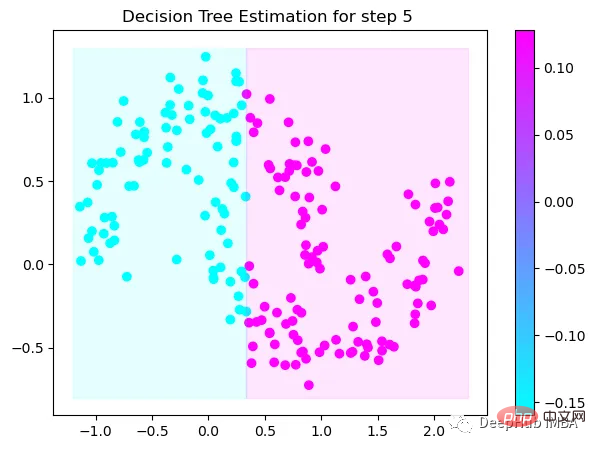
Tree Split for 0 and level 0.3370491564273834

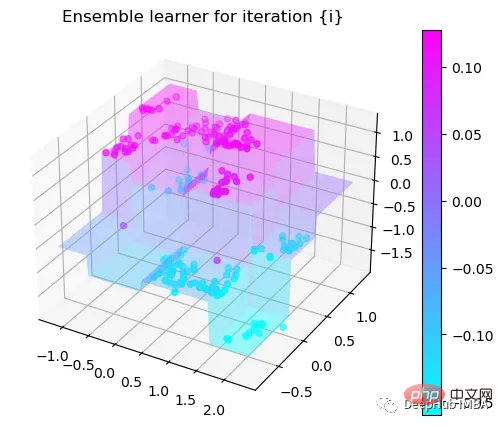
第6次决策

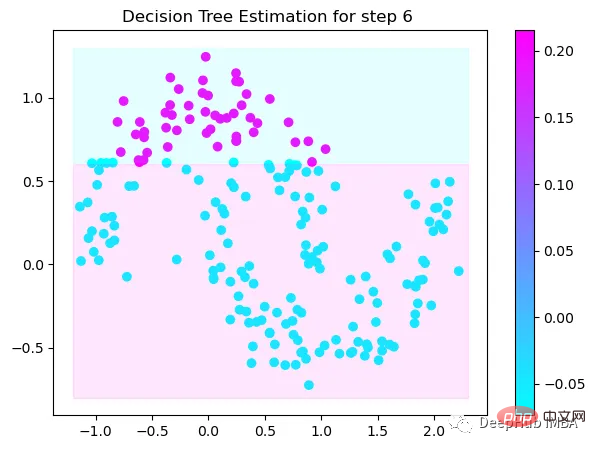
Tree Split for 1 and level 0.022058885544538498

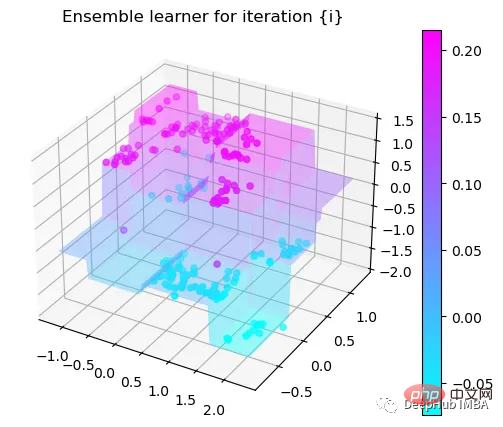
第7次决策

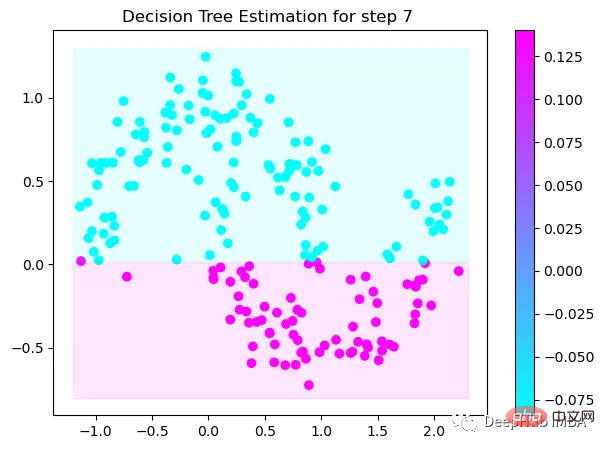
Tree Split for 0 and level -0.3030575215816498

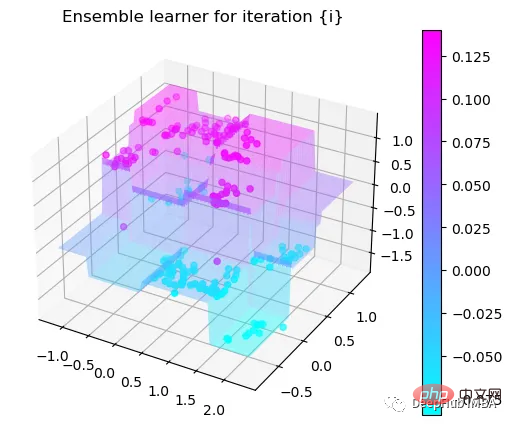
第8次决策

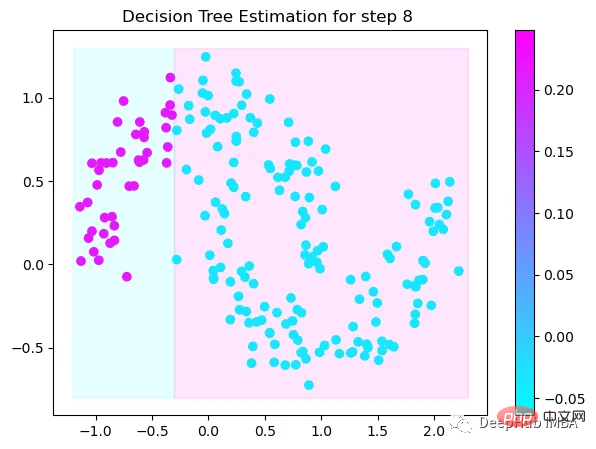
Tree Split for 0 and level 0.6119407713413239

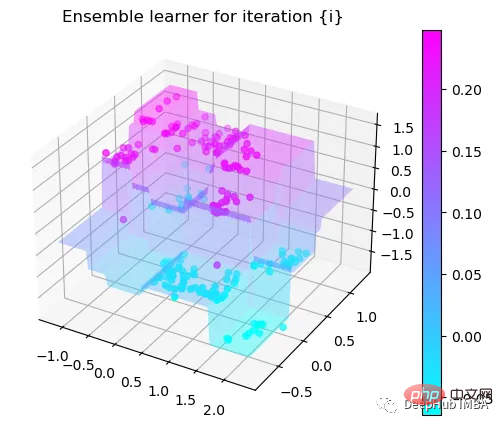
第9次决策

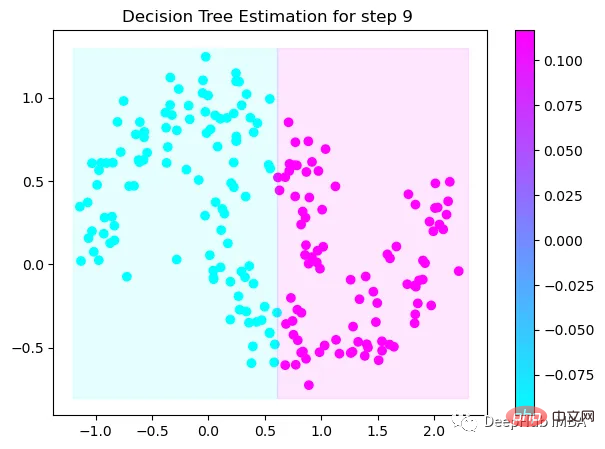
可以看到通过9次的计算，基本上已经把上面的分类进行了区分

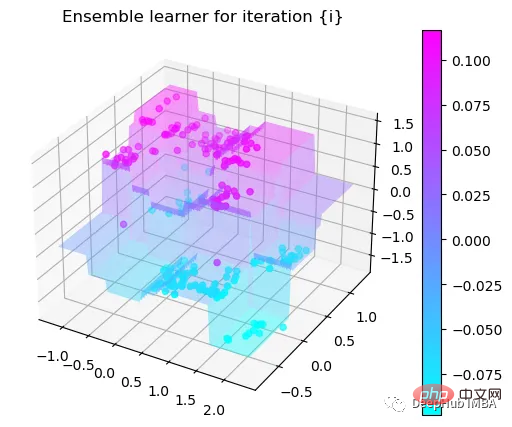
我们这里的学习器都是非常简单的决策树，只沿着一个特征分裂!但整体模型在每次决策后边的越来越复杂，并且整体误差逐渐减小。

plt.plot(rmses)

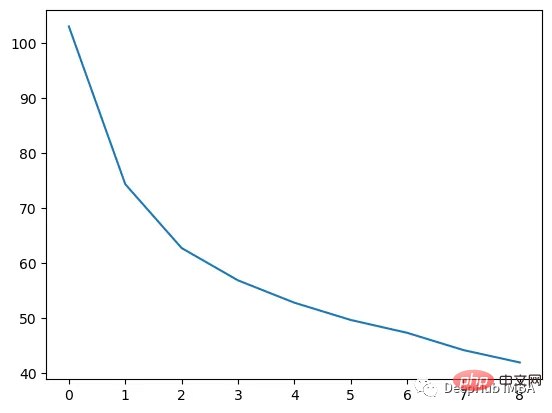
这也就是上图中我们看到的能够正确区分出了大部分的分类

如果你感兴趣可以使用下面代码自行实验：

​​https://www.php.cn/link/bfc89c3ee67d881255f8b097c4ed2d67​​

Das obige ist der detaillierte Inhalt vonSchrittweise Visualisierung des Entscheidungsprozesses des Gradient-Boosting-Algorithmus. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!