Die Shanghai Jiao Tong University und andere schlugen eine neue Methode der adaptiven lokalen Aggregation vor, die SOTA um 3,27 % übertraf

Dieser Artikel stellt einen in AAAI 2023 enthaltenen Artikel vor. Der Artikel wurde von Professor Hua Yang vom Shanghai Key Laboratory of Scalable Computing and Systems an der Shanghai Jiao Tong University, der Queen's University Belfast und dem Lehrer Wang Hao der Louisiana State University gemeinsam verfasst es zusammen.

• Papier-Link: https://arxiv.org/abs/2212.01197​
• Code-Link (einschließlich Anweisungen zur Verwendung des ALA-Moduls): https://github .com/ TsingZ0/FedALA​

Dieses Papier schlägt eine adaptive lokale Aggregationsmethode für föderiertes Lernen vor, die die Probleme beim föderierten Lernen bewältigt, indem sie die vom Kunden benötigten Informationen automatisch aus dem globalen Modell erfasst. Der Autor verglich 11 SOTA-Modelle und erzielte eine hervorragende Leistung von 3,27 % über der optimalen Methode. Der Autor wandte das adaptive lokale Aggregationsmodul auf andere föderierte Lernmethoden an und erzielte eine Verbesserung von bis zu 24,19 %.

1 Einführung

Federated Learning (FL) hilft Menschen dabei, den in Benutzerdaten enthaltenen Wert vollständig zu erkunden und gleichzeitig die Privatsphäre zu schützen, indem private Benutzerdaten lokal gespeichert werden, ohne sie zu verbreiten. Da die Daten zwischen Clients jedoch nicht sichtbar sind, ist die statistische Heterogenität der Daten (nicht unabhängige und identisch verteilte Daten (Nicht-IID) und Ungleichgewicht des Datenvolumens) zu einer der großen Herausforderungen von FL geworden. Die statistische Heterogenität der Daten macht es für herkömmliche föderierte Lernmethoden (wie FedAvg usw.) schwierig, durch FL-Prozesstraining ein einziges globales Modell zu erhalten, das für jeden Kunden geeignet ist.

In den letzten Jahren haben Methoden des personalisierten föderierten Lernens (pFL) aufgrund ihrer Fähigkeit, mit der statistischen Heterogenität von Daten umzugehen, zunehmend Beachtung gefunden. Im Gegensatz zur herkömmlichen FL, die ein qualitativ hochwertiges globales Modell anstrebt, zielt der pFL-Ansatz darauf ab, mit der kollaborativen Rechenleistung des föderierten Lernens ein personalisiertes Modell zu trainieren, das für jeden Kunden geeignet ist. Bestehende pFL-Forschung zu Aggregationsmodellen auf dem Server kann in die folgenden drei Kategorien unterteilt werden:

(1) Methoden zum Erlernen eines einzelnen globalen Modells und zur Feinabstimmung, einschließlich Per-FedAvg und FedRep

( 2) Methoden zum Erlernen zusätzlicher personalisierter Modelle, einschließlich pFedMe und Ditto;

(3) Methoden zum Erlernen lokaler Modelle durch personalisierte Aggregation (oder lokale Aggregation), einschließlich FedAMP, FedPHP, FedFomo, APPLE und PartialFed.

pFL-Methoden in den Kategorien (1) und (2) verwenden alle Informationen aus dem globalen Modell für die lokale Initialisierung (bezieht sich auf die Initialisierung des lokalen Modells vor dem lokalen Training bei jeder Iteration). Im globalen Modell sind jedoch nur Informationen für den Kunden von Vorteil, die die Qualität des lokalen Modells verbessern (vom Kunden benötigte Informationen, die die lokalen Trainingsziele erfüllen). Globale Modelle lassen sich schlecht verallgemeinern, da sie sowohl Informationen enthalten, die von einem einzelnen Kunden benötigt werden, als auch solche, die er nicht benötigt. Daher schlagen Forscher pFL-Methoden in Kategorie (3) vor, um die von jedem Kunden im globalen Modell benötigten Informationen durch personalisierte Aggregation zu erfassen. Die pFL-Methoden in Kategorie (3) existieren jedoch weiterhin (a) berücksichtigen nicht die lokalen Trainingsziele des Kunden (wie FedAMP und FedPHP), (b) haben hohe Rechen- und Kommunikationskosten (wie FedFomo und APPLE), (c ) Datenschutzprobleme wie Leakage (wie FedFomo und APPLE) und (d) Diskrepanz zwischen personalisierter Aggregation und lokalen Trainingszielen (wie PartialFed). Da diese Methoden außerdem umfangreiche Änderungen am FL-Prozess vornehmen, können die von ihnen verwendeten personalisierten Aggregationsmethoden in den meisten vorhandenen FL-Methoden nicht direkt verwendet werden.

Um die vom Kunden benötigten Informationen aus dem globalen Modell genau zu erfassen, ohne die Kommunikationskosten in jeder Iteration im Vergleich zu FedAvg zu erhöhen, schlägt der Autor eine adaptive lokale Aggregationsmethode für föderiertes Lernen (FedALA) vor. Wie in Abbildung 1 dargestellt, erfasst FedALA die erforderlichen Informationen im globalen Modell, indem es vor jedem lokalen Training das globale Modell mit dem lokalen Modell über das adaptive lokale Aggregationsmodul (ALA) aggregiert. Da FedALA im Vergleich zu FedAvg nur ALA verwendet, um den lokalen Modellinitialisierungsprozess in jeder Iteration zu ändern, ohne andere FL-Prozesse zu ändern, kann ALA direkt auf die meisten anderen vorhandenen FL-Methoden angewendet werden, um deren individuelle Leistung zu verbessern.

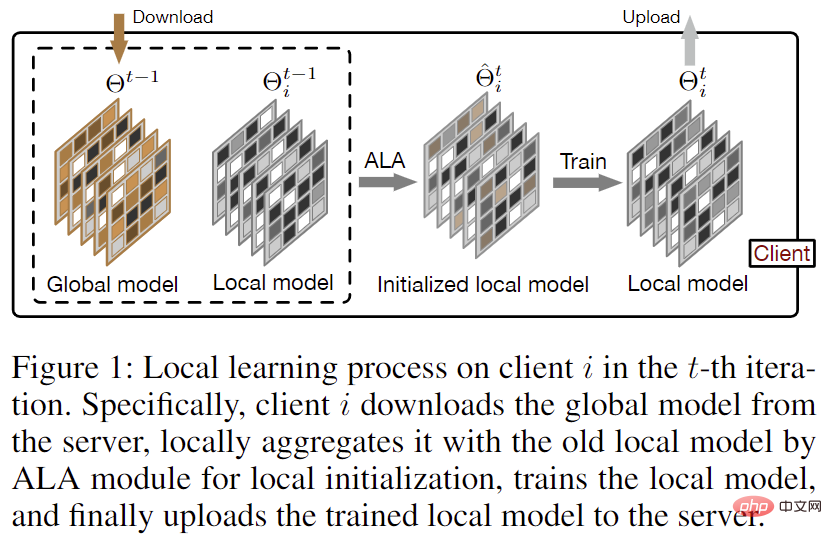
Abbildung 1: Lokaler Lernprozess auf dem Client in Iteration

2 Methode

2.1 Adaptive Local Aggregation (ALA) ​

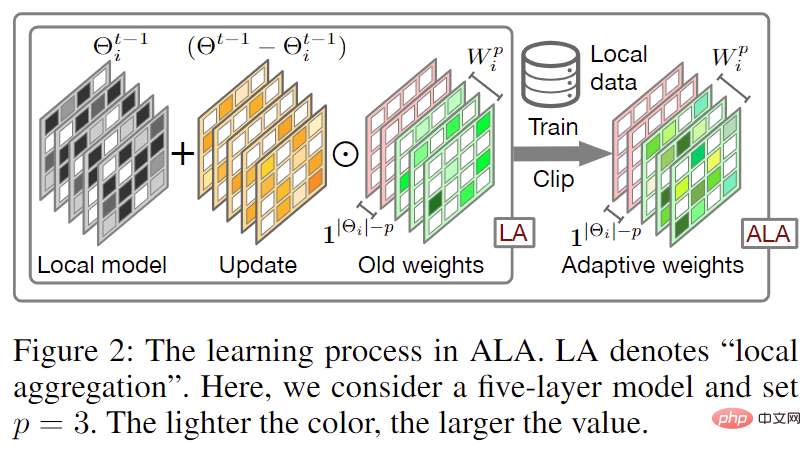
Abbildung 2: Adaptive Local. Aggregation (ALA) Prozess

Der Prozess der adaptiven lokalen Aggregation (ALA) ist in Abbildung 2 dargestellt. Im Vergleich zum traditionellen föderierten Lernen, bei dem das lokale Modell direkt mit dem heruntergeladenen globalen Modell überschrieben wird, um ein lokal initialisiertes Modell (d. h. ) zu erhalten, lernt FedALA lokale Modelle für jeden Parameter Aggregierte Gewichte für die adaptive lokale Aggregation.

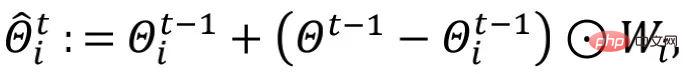
Unter anderem nennt der Autor 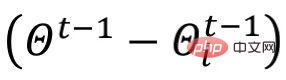„Update“. Darüber hinaus implementiert der Autor die Regularisierung durch die elementweise Gewichtsbeschneidungsmethode 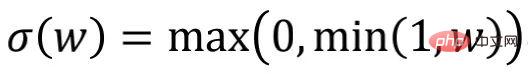und begrenzt die Werte in 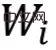auf [0,1].

Da das Netzwerk der unteren Schicht des tiefen neuronalen Netzwerks (DNN) tendenziell relativ mehr allgemeine Informationen lernt als die höhere Schicht, und die allgemeinen Informationen die Informationen sind, die von jedem lokalen Modell benötigt werden, also das Netzwerk der unteren Schicht im globalen Modell Die meisten Informationen stimmen mit den Informationen überein, die von Netzwerken auf niedrigerer Ebene im lokalen Modell benötigt werden. Um den Rechenaufwand zum Erlernen lokaler Aggregationsgewichte zu reduzieren, führt der Autor einen Hyperparameter p ein, um den Umfang von ALA zu steuern, sodass die Netzwerkparameter der unteren Schicht im globalen Modell das Netzwerk der unteren Schicht im lokalen Modell direkt abdecken nur in der höheren Ebene ALA aktivieren.

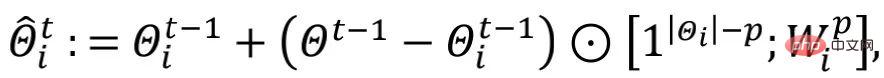
Unter diesen stellt die Anzahl der neuronalen Netzwerkschichten (oder die Anzahl der neuronalen Netzwerkblöcke) in dar, stimmt mit der Form des Low-Level-Netzwerks in überein und stimmt mit überein. Die verbleibenden p-Schicht-Hochebenennetzwerke haben die gleiche Form.

Der Autor initialisiert alle Werte in auf 1 und aktualisiert basierend auf dem alten während jeder Runde der lokalen Initialisierung. Um den Rechenaufwand weiter zu reduzieren, verwendet der Autor Zufallsstichproben s

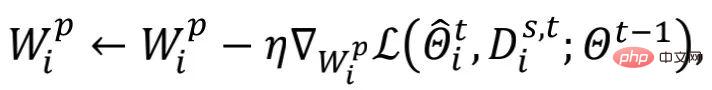
wobei die Lernrate der Aktualisierung ist. Während des Lernprozesses friert der Autor andere trainierbare Parameter außer ein.

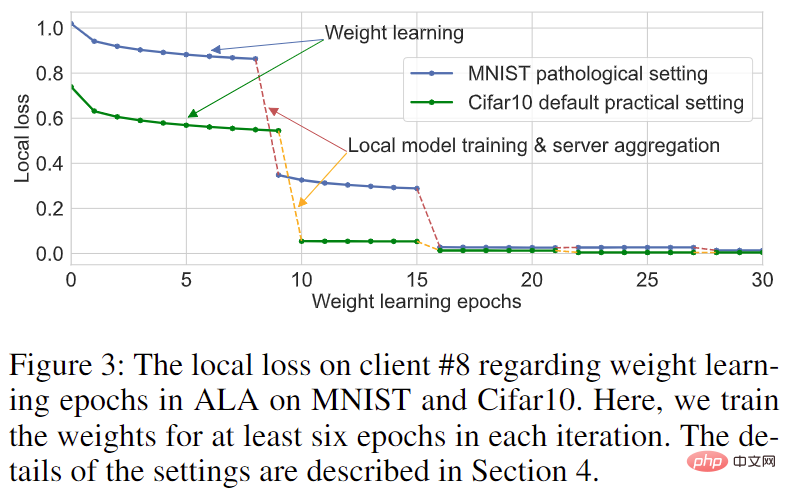
Abbildung 3: Lernkurve von Client 8 für MNIST- und Cifar10-Datensätze

Durch die Wahl eines kleineren p-Werts kann die FedALA-Leistung deutlich verbessert werden, ohne die Leistung von FedALA Reduce nahezu zu beeinträchtigen die für das Training in ALA erforderlichen Parameter. Darüber hinaus stellten die Autoren, wie in Abbildung 3 dargestellt, fest, dass, sobald es im ersten Training auf Konvergenz trainiert wurde, es keinen großen Einfluss auf die Qualität des lokalen Modells hat, selbst wenn es in nachfolgenden Iterationen trainiert wird. Das heißt, jeder Kunde kann das alte wiederverwenden, um die benötigten Informationen zu erfassen. Der Autor wendet die Methode der Feinabstimmung in nachfolgenden Iterationen an, um den Rechenaufwand zu reduzieren.

2.2 ALA-Analyse​

Ohne die Analyse zu beeinflussen, ignoriert der Autor der Einfachheit halber und geht von aus. Gemäß der obigen Formel können wir 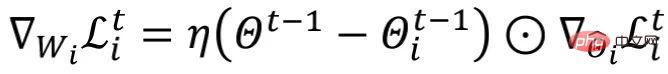erhalten, wobei 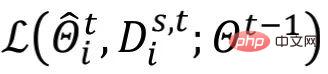darstellt. Autoren können sich die Aktualisierung von 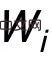in ALA als Aktualisierung von vorstellen.

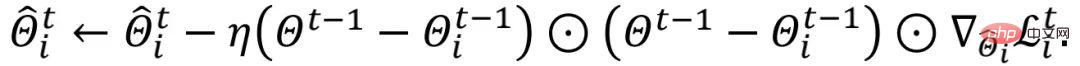
Der Verlaufsterm wird in jeder Runde Element für Element skaliert. Anders als bei der lokalen Modelltrainings- (oder Feinabstimmungs-)Methode kann der obige Aktualisierungsprozess von die gemeinsamen Informationen im globalen Modell wahrnehmen. Zwischen verschiedenen Iterationsrunden führt das sich dynamisch ändernde 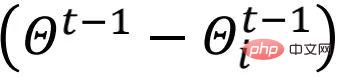dynamische Informationen in das ALA-Modul ein und erleichtert so die Anpassung von FedALA an komplexe Umgebungen.

3 Experiment

Der Autor verwendete ResNet-18, um die Auswirkungen der Hyperparameter s und p auf FedALA auf den Tiny-ImageNet-Datensatz in einer praktischen datenheterogenen Umgebung zu untersuchen, wie in Tabelle 1 gezeigt. Beispielsweise kann die Verwendung von mehr zufällig ausgewählten lokalen Trainingsdaten für das Lernen des ALA-Moduls zu einer besseren Leistung des personalisierten Modells führen, erhöht jedoch auch den Rechenaufwand. Bei Verwendung von ALA kann die Größe der s basierend auf der Rechenleistung jedes Clients angepasst werden. Wie aus der Tabelle hervorgeht, weist FedALA auch bei Verwendung extrem kleiner s (z. B. s=5) immer noch eine hervorragende Leistung auf. Für p haben unterschiedliche p-Werte fast keinen Einfluss auf die Leistung des personalisierten Modells, es gibt jedoch einen großen Unterschied im Rechenaufwand. Dieses Phänomen zeigt einerseits auch die Wirksamkeit von Methoden wie FedRep, das das Modell teilt und die neuronale Netzwerkschicht in der Nähe der Ausgabe behält, ohne sie auf den Client hochzuladen. Bei Verwendung von ALA können wir einen kleineren und geeigneten p-Wert verwenden, um den Rechenaufwand weiter zu reduzieren und gleichzeitig die Leistungsfähigkeit des personalisierten Modells sicherzustellen.

Tabelle 1: Forschung zu Hyperparametern und deren Auswirkungen auf FedALA

Der Autor verglich FedALA mit 11 in einer heterogenen Umgebung mit pathologischen Daten und einer heterogenen Umgebung mit praktischen Daten. Mehrere SOTA-Methoden wurden verglichen und im Detail analysiert. Wie in Tabelle 2 gezeigt, zeigen die Daten, dass FedALA diese 11 SOTA-Methoden in allen Fällen übertrifft, wobei „TINY“ die Verwendung eines 4-Schicht-CNN auf Tiny-ImageNet bedeutet. Beispielsweise übertrifft FedALA im TINY-Fall die optimale Basislinie um 3,27 %.

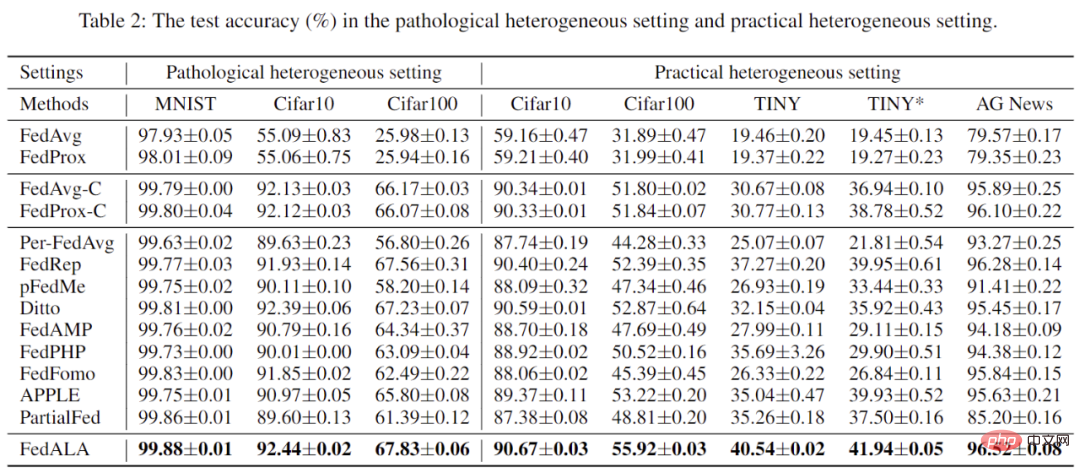
Tabelle 2: Experimentelle Ergebnisse unter heterogenen Umgebungen mit pathologischen und realen Daten

#🎜 🎜#

Darüber hinaus bewertete der Autor auch die Leistung von FedALA in verschiedenen heterogenen Umgebungen und der Gesamtzahl der Kunden. Wie in Tabelle 3 gezeigt, behält FedALA unter diesen Bedingungen immer noch eine hervorragende Leistung bei.

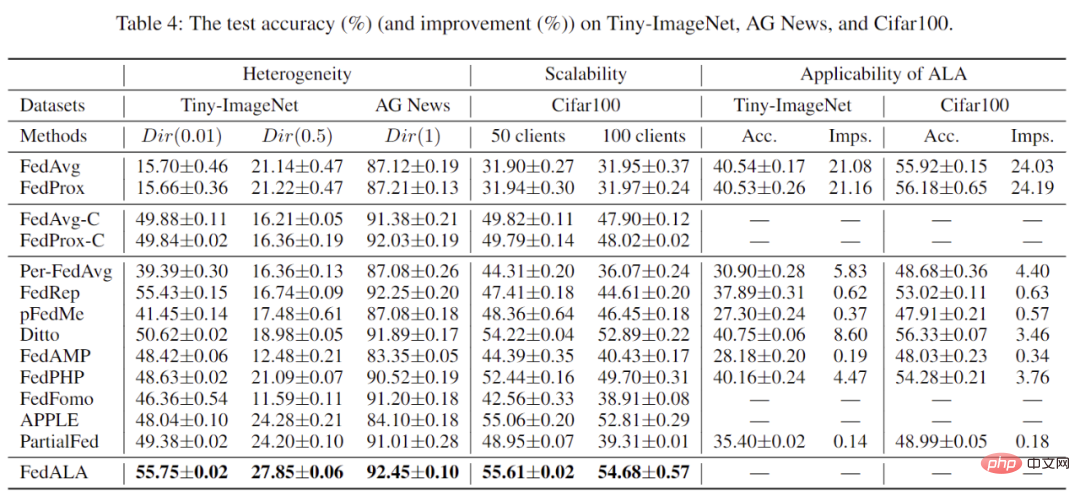
Tabelle 3: Weitere experimentelle Ergebnisse Nach dem Experiment Die Ergebnisse in Tabelle 3 zeigen, dass durch die Anwendung des ALA-Moduls auf andere Methoden eine Verbesserung von bis zu 24,19 % erzielt werden kann.

Schließlich visualisierte der Autor auch die Auswirkungen der Hinzufügung des ALA-Moduls auf das Modelltraining im ursprünglichen FL-Prozess auf MNIST, wie in Abbildung 4 dargestellt. Wenn ALA nicht aktiviert ist, stimmt der Modelltrainingsverlauf mit der Verwendung von FedAvg überein. Sobald ALA aktiviert ist, kann das Modell direkt auf das optimale Ziel hin optimiert werden, wobei die für sein Training erforderlichen Informationen im globalen Modell erfasst werden.

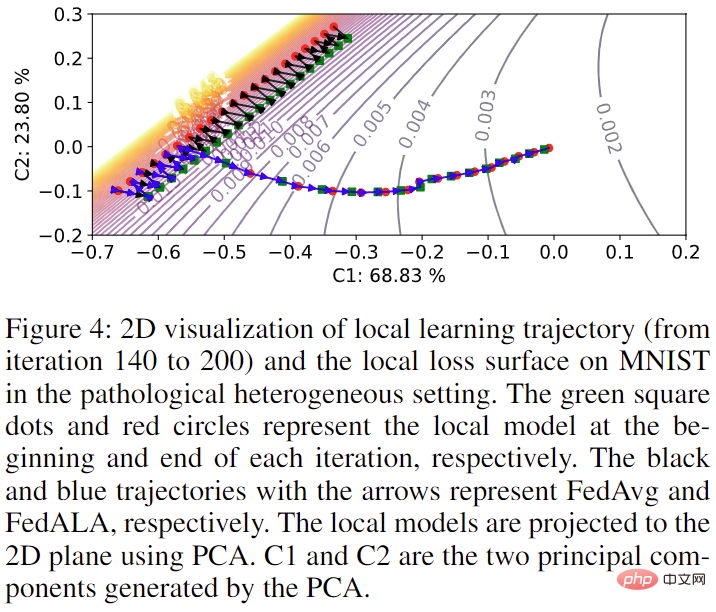Abbildung 4: Visualisierung der Modelltrainingsbahn bei Kunde Nr. 4

# 🎜🎜#

Das obige ist der detaillierte Inhalt vonDie Shanghai Jiao Tong University und andere schlugen eine neue Methode der adaptiven lokalen Aggregation vor, die SOTA um 3,27 % übertraf. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!