„Sparse Coding“ geht von der Theorie in die Praxis! Professor Ma Yis neue Arbeit in NeurIPS 2022: Sparse-Faltungsleistung und Robustheit übertreffen ResNet

Obwohl tiefe neuronale Netze eine starke empirische Leistung bei der Bildklassifizierung aufweisen, werden solche Modelle oft als „Black Boxes“ betrachtet und am meisten dafür kritisiert, dass sie „schwer zu erklären“ sind.

Im Gegensatz dazu sind sparse-Faltungsmodelle auch leistungsstarke Werkzeuge zur Analyse natürlicher Bilder, die davon ausgehen, dass ein Signal aus einer linearen Kombination mehrerer Elemente im Faltungswörterbuch bestehen kann. Um es auszudrücken, hat es gute theoretische Eigenschaften Interpretierbarkeit und biologische Plausibilität.

Aber in praktischen Anwendungen zeigt das Sparse-Faltungsmodell, obwohl es prinzipiell funktioniert, nicht die Leistungsvorteile, die es im Vergleich zu empirisch entworfenen tiefen Netzwerken verdient. Kürzlich hat die Forschungsgruppe von Professor Ma Yi auf der NeurIPS 2022 einen neuen Artikel veröffentlicht, in dem sie die Anwendung von Modellen mit geringer Faltung in der Bildklassifizierung untersucht und die empirische Leistung und Zuverlässigkeit von Modellen mit geringer Übereinstimmung bei der Interpretation erfolgreich gelöst hat.

Papierlink: https://arxiv.org/pdf/2210.12945.pdf​

Codelink: https://github.com/Delay-Xili/SDNet​

Die im Artikel vorgeschlagene differenzierbare Optimierungsschicht

verwendet

Convolutional Sparse Coding (CSC) , um die standardmäßige quasi-Faltungsschicht zu ersetzen. Die Ergebnisse zeigen, dass diese Modelle im Vergleich zu herkömmlichen neuronalen Netzen eine gleich starke empirische Leistung bei CIFAR-10-, CIFAR-100- und ImageNet-Datensätzen aufweisen.

Durch Ausnutzung der robusten Wiederherstellungseigenschaften der spärlichen Modellierung zeigen die Forscher außerdem, dass diese Modelle mit nur einem einfachen geeigneten Kompromiss zwischen spärlicher Regularisierung und Datenrekonstruktionstermen Eingabeverfälschungen überstehen können und kontroverse Störungen robuster sind .

Professor Ma Yi erhielt 1995 einen Doppel-Bachelor-Abschluss in Automatisierung und angewandter Mathematik von der Tsinghua-Universität, studierte anschließend an der University of California, Berkeley, USA, und erhielt 1997 einen Master-Abschluss in EECS Master-Abschluss in Mathematik und Ph.D. in EECS im Jahr 2000, Bachelor of Science.

Nach seinem Abschluss lehrte er an der University of Illinois in Urbana-Champaign und wurde der jüngste außerordentliche Professor in der Geschichte der Fakultät für Elektrotechnik und Informationstechnik.

Im Jahr 2009 war er als leitender Forscher in der Visual Computing Group von Microsoft Research Asia tätig. Im Jahr 2014 wechselte er hauptberuflich an die School of Information Science and Technology der ShanghaiTech University.

Tritt 2018 der University of California, Berkeley und dem Tsinghua-Berkeley Shenzhen Institute bei. Derzeit ist er Professor am Fachbereich Elektrotechnik und Informatik der University of California, Berkeley. Außerdem ist er IEEE Fellow, ACM Fellow und SIAM Fellow

Die Forschung von Professor Ma Yi umfasst 3D-Computervision, niedrigdimensionale Modelle für hochdimensionale Daten, Skalierbarkeitsoptimierung und maschinelles Lernen. Zu den jüngsten Forschungsthemen gehören groß angelegte geometrische 3D-Rekonstruktion und -Interaktion die Beziehung zwischen niedrigdimensionalen Modellen und tiefen Netzwerken.

Sparse Convolution

Obwohl tiefe Faltungsnetzwerke (ConvNets) zur Mainstream-Methode für die Bildklassifizierung geworden sind und ihre Leistung andere Modelle übertrifft, sind ihre internen Komponenten wie Faltung, nichtlineare Funktionen und Normalisierung usw. Die spezifische Bedeutung der Daten wurden noch nicht erklärt.

Während die Modellierung spärlicher Daten, unterstützt durch die Fähigkeit, interpretierbare Darstellungen und starke theoretische Garantien (z. B. den Umgang mit beschädigten Daten) zu lernen, in vielen Signal- und Bildverarbeitungsanwendungen weit verbreitet ist, ist ihre Leistung bei Daten wie ImageNet The Die Klassifizierungsleistung am Set ist immer noch schlechter als bei empirischen Tiefenmodellen.

Selbst spärliche Modelle mit starker Leistung weisen immer noch Mängel auf:

1) Die Netzwerkstruktur muss speziell entworfen werden, was die Anwendbarkeit des Modells einschränkt.

2) Die Berechnungsgeschwindigkeit des Trainings beträgt mehrere Größenordnungen Größe langsamer;

3) Es zeigt keine offensichtlichen Vorteile in der Interpretierbarkeit und Robustheit.

Die Forscher schlugen in diesem Artikel ein visuelles Erkennungsframework vor und demonstrierten, dass spärliche Modellierung durch ein einfaches Design mit Deep Learning kombiniert werden kann, vorausgesetzt, dass die Ebeneneingabe aus einigen Atomen in einem Wörterbuch bestehen kann, das von allen Datenpunkten gemeinsam genutzt wird (Atome) und erreicht so die gleiche Leistung wie Standard-ConvNets bei gleichzeitig besserer hierarchischer Interpretierbarkeit und Stabilität.

Diese Methode kapselt spärliche Modellierung in einer impliziten Schicht und verwendet sie als Ersatz für die Faltungsschicht in Standard-ConvNets.

Im Vergleich zur expliziten Funktion, die in der klassischen vollständig verbundenen oder Faltungsschicht verwendet wird, verwendet die verborgene Schicht eine implizite Funktion. Die verborgene Schicht in diesem Artikel wird basierend auf dem Optimierungsproblem der Eingabe- und Gewichtsparameter der Schicht definiert, und die Ausgabe der verborgenen Schicht ist die Lösung des Optimierungsproblems.

Bei einem mehrdimensionalen Eingangssignal kann die Funktion der Ebene so definiert werden, dass eine umgekehrte Zuordnung zu einer besseren spärlichen Ausgabe erfolgt. Die Anzahl der Ausgabekanäle kann sich von der Eingabe unterscheiden, sodass das obige Lasso optimal ist Typoptimierungsprobleme können spärlich gelöst werden.

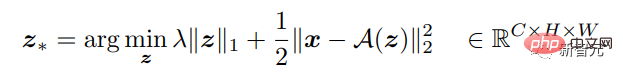
Diese verborgene Schicht implementiert das Convolutional Sparse Coding (CSC)-Modell, bei dem das Eingangssignal durch eine spärliche lineare Kombination von Atomen in einem Faltungswörterbuch angenähert wird. Dieses Faltungswörterbuch kann als Parameter der CSC-Schicht betrachtet werden, die durch Backpropagation trainiert wird.

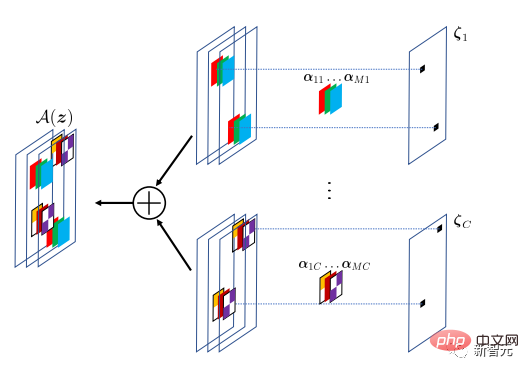
Das Ziel des CSC-Modells besteht darin, das Eingangssignal durch den A(z)-Operator zu rekonstruieren, wobei die Feature-Map z die Position und den Wert des Faltungsfilters in A angibt. Um Modellierungsunterschiede tolerieren zu können, muss die Rekonstruktion nicht exakt sein.

Basierend auf der ermittelten Eingabe-Ausgabe-Zuordnung der CSC-Schicht kann die Vorwärtsausbreitung durch Lösen der relevanten Optimierung durchgeführt werden, und die Rückausbreitung kann durchgeführt werden, indem der Gradient der optimalen Koeffizientenlösung relativ zum Eingabe-x und -Parameter ermittelt wird A .

Dann kann das gesamte Netzwerk mit CSC-Schicht aus den gekennzeichneten Daten durchgängig trainiert werden, indem der Kreuzentropieverlust minimiert wird.

Experimentelle Ergebnisse

Vergleich der Klassifizierungsleistung​

Die im Experiment verwendeten Datensätze sind CIFAR-10 und CIFAR-100, jeder Datensatz enthält 50.000 Bilder und 10.000 Testbilder, jedes Bild hat eine Größe von 32×32 und RGB-Kanäle.

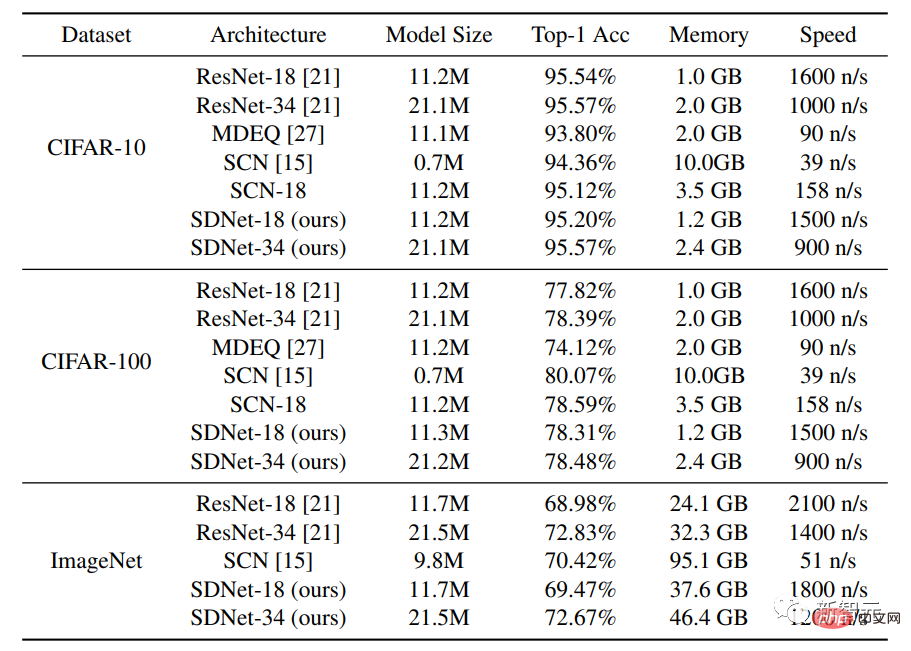
Neben dem Vergleich der Methode mit den Standard-Netzwerkarchitekturen ResNet-18 und ResNet-34 verglichen die Forscher auch das MDEQ-Modell mit Hidden-Layer-Architektur und SCN mit spärlicher Modellierungsarchitektur.

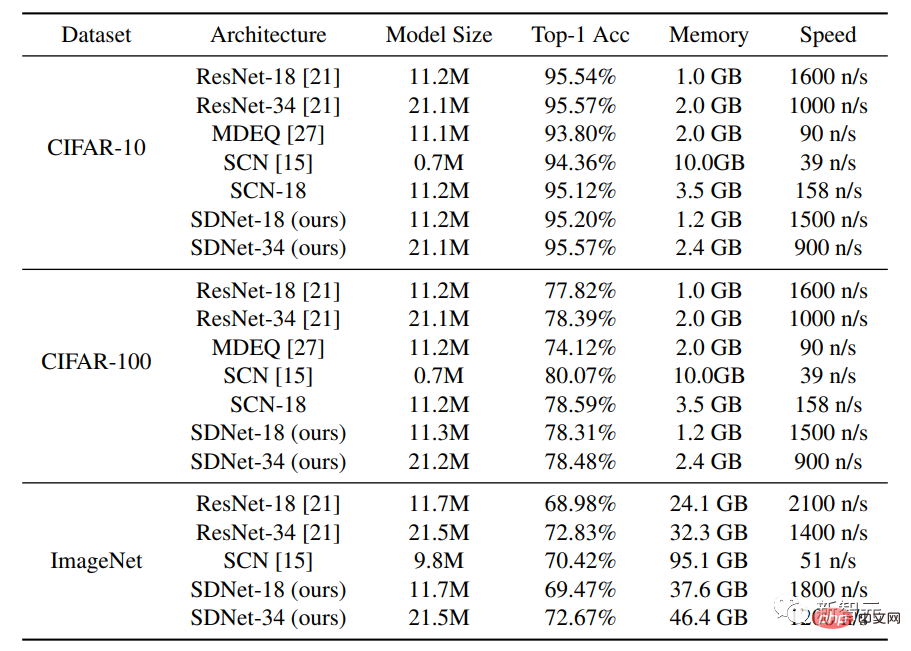
Die experimentellen Ergebnisse zeigen, dass bei einem ähnlichen Modellmaßstab die Top-1-Genauigkeit von SDNet-18/34 ähnlich oder höher als die von ResNet-18/34 ist und gleichzeitig eine ähnliche Inferenzgeschwindigkeit aufweist. Die Ergebnisse zeigen das Potenzial dieses Netzwerks als leistungsstarke Alternative zu bestehenden datengesteuerten Modellen, da SDNet-Modelle zusätzliche Vorteile beim Umgang mit beschädigten Bildern bieten.

Nach dem Vergleich des SDNet-18-Modells mit dem MDEQ-Modell mit ähnlicher Modellgröße kann festgestellt werden, dass SDNet-18 nicht nur genauer als MDEQ, sondern auch viel schneller (>7-mal) ist. Es ist zu beachten, dass MDEQ beschädigte Daten nicht wie SDNet verarbeiten kann.

Das SCN-Netzwerk, das ebenfalls Sparse-Modellierung verwendet, hat eine Top-1-Genauigkeit erreicht, aber ein wichtiger Nachteil von SCN ist, dass seine Trainingsgeschwindigkeit sehr langsam ist. Der Grund dafür könnte sein, dass SCN ein Patch-basiertes Sparse-Coding-Modell verwendet Für Bilder muss es im Vergleich zum Faltungssparse-Codierungsmodell bei jedem Vorwärtsdurchlauf spärlichere Codierungsprobleme lösen und kann nicht von paralleler Berechnung profitieren.

Robuste Inferenzbehandlung von Eingabestörungen

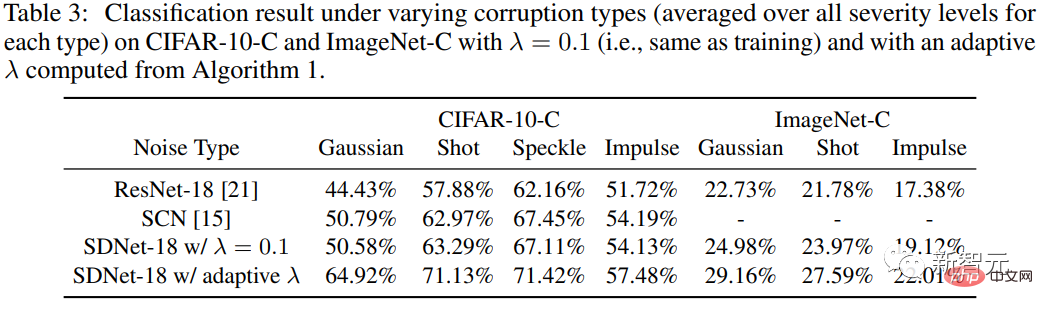
Um die Robustheit der Methode gegenüber Eingabestörungen zu testen, verwendeten die Forscher den CIFAR-10-C-Datensatz, in dem die Daten durch verschiedene Arten von synthetischem Rauschen beeinflusst wurden schwer beschädigt.

Da die CSC-Schicht im Modell die eingangsbezogene Differenz zwischen dem Eingangssignal und dem rekonstruierten Signal bestraft, sollte SDNet theoretisch besser für die Verarbeitung von additivem Rauschen geeignet sein.

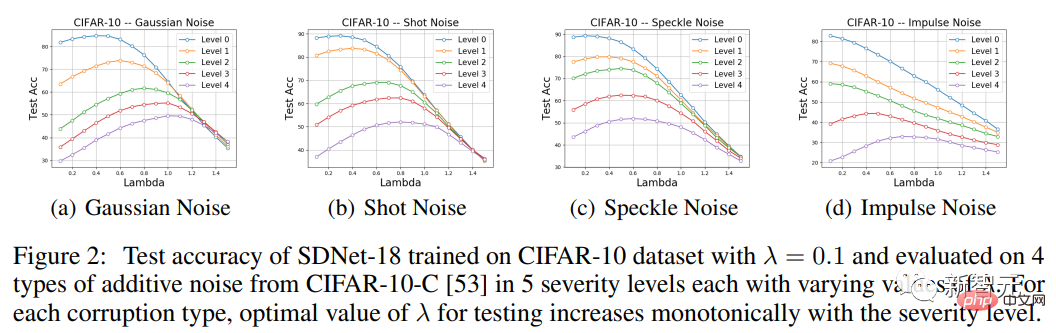
Der experimentelle Teil konzentriert sich also hauptsächlich auf die vier Arten von additivem Rauschen in CIFAR-10-C, nämlich Gaußsches Rauschen, Schrotrauschen, Speckle-Rauschen und Impulsrauschen, und bewertet dann die Genauigkeit von SDNet-18. und seine Leistung wird mit ResNet-18 verglichen.

Es ist ersichtlich, dass bei verschiedenen Arten von Geräuschen und unterschiedlichen Schweregraden (außer Impulsgeräuschen der Stufen 0, 1 und 2) die richtige Wahl eines λ-Werts, der sich von dem während des Trainings verwendeten unterscheidet, zur Verbesserung der Testleistung beitragen kann.

Insbesondere die Genauigkeitskurve als Funktion von λ weist eine unimodale Form auf, wobei die Leistung zunächst zunimmt und dann abnimmt. Darüber hinaus steigt bei jedem Datenbeschädigungstyp der λ-Wert, bei dem Leistungsspitzen erreicht werden, monoton mit der Schwere der Beschädigung, eine Beobachtung, die mit den Erwartungen übereinstimmt.

Umgang mit gegnerischen Störungen

Die Forscher verwendeten PGD, um gegnerische Störungen auf SDNet (λ=0,1) im CIFAR-10-Testdatensatz zu erzeugen. Das L∞-Paradigma der Störung beträgt 8/255 und Die Normalform der Störung L2 beträgt 0,5.

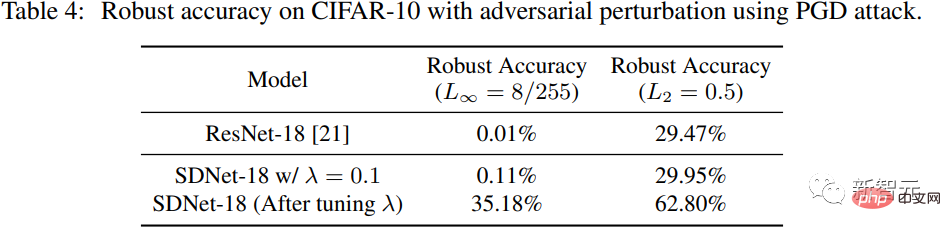
Im Vergleich zu ResNet-18 können wir sehen, dass die Leistung von SDNet bei λ = 0,1 nicht viel besser ist als die von ResNet, die Robustheitsgenauigkeit jedoch durch Anpassen des Parameters λ erheblich verbessert werden kann .

Das obige ist der detaillierte Inhalt von„Sparse Coding“ geht von der Theorie in die Praxis! Professor Ma Yis neue Arbeit in NeurIPS 2022: Sparse-Faltungsleistung und Robustheit übertreffen ResNet. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!