Eine auf einem neuronalen Netzwerk basierende Strategie zur Verbesserung von Quantensimulationen

Neueste Quantencomputer bieten eine vielversprechende Plattform für die Ermittlung des Grundzustands von Quantensystemen, eine grundlegende Aufgabe in der Physik, Chemie und Materialwissenschaft. Neuere Methoden sind jedoch durch Rauschen und begrenzte aktuelle Quantenhardwareressourcen begrenzt.

Forscher der University of Waterloo in Kanada haben die neuronale Fehlerminderung eingeführt, die neuronale Netze nutzt, um die Schätzungen des Grundzustands und der Grundzustandsobservablen zu verbessern, die mithilfe aktueller Quantensimulationen gewonnen wurden. Um die breite Anwendbarkeit der Methode zu demonstrieren, verwendeten die Forscher eine neuronale Fehlerminderung, um die Grundzustände der molekularen H2- und LiH-Hamiltonoperatoren zu finden, die mit einem Variationsquanteneigenlöser sowie dem Gitter-Schwinger-Modell erstellt wurden.

Experimentelle Ergebnisse zeigen, dass die Abschwächung neuronaler Fehler numerische und experimentelle Variations-Quantensignatur-Löserberechnungen verbessert, um Fehler mit geringer Energie, hohe Wiedergabetreue und Robustheit gegenüber komplexeren Observablen (z. B. Ordnungsparameter und Verschränkungsentropie) zu erzeugen, ohne dass zusätzliche Schätzungen erforderlich sind Quantenressourcen. Darüber hinaus ist die Abschwächung neuronaler Fehler unabhängig vom verwendeten Quantenzustandsvorbereitungsalgorithmus, der ihn implementierenden Quantenhardware und den spezifischen Rauschkanälen, die das Experiment beeinflussen, was zu seiner Vielseitigkeit als Quantensimulationswerkzeug beiträgt.

Die Forschung trägt den Titel „Neural Error Mitigation of Near-Term Quantum Simulations“ und wurde am 20. Juli 2022 in „Nature Machine Intelligence“ veröffentlicht.

Seit dem frühen 20. Jahrhundert entwickeln Wissenschaftler umfassende Theorien, die das Verhalten quantenmechanischer Systeme beschreiben. Allerdings übersteigen die zur Untersuchung dieser Systeme erforderlichen Rechenkosten häufig die Möglichkeiten aktueller wissenschaftlicher Rechenmethoden und Hardware. Daher bleibt die rechnerische Undurchführbarkeit ein Hindernis für die praktische Anwendung dieser Theorien auf wissenschaftliche und technische Probleme.

Die Simulation von Quantensystemen auf Quantencomputern (hier Quantensimulation genannt) ist vielversprechend bei der Überwindung dieser Hindernisse und war eine grundlegende treibende Kraft hinter dem Konzept und der Entwicklung von Quantencomputern. Insbesondere Quantensimulationen der Grund- und stationären Zustände von Quanten-Vielteilchensystemen, die über die Möglichkeiten klassischer Computer hinausgehen, dürften erhebliche Auswirkungen auf die Kernphysik, die Teilchenphysik, die Quantengravitation, die Physik der kondensierten Materie, die Quantenchemie und die Materialwissenschaften haben . Die Fähigkeiten aktueller und künftiger Quantencomputer werden weiterhin durch Einschränkungen wie die Anzahl der Qubits und die Auswirkungen von Rauschen begrenzt. Die Quantenfehlerkorrekturtechnologie kann durch Rauschen verursachte Fehler beseitigen und bietet so eine Möglichkeit für fehlertolerantes Quantencomputing. In der Praxis verursacht die Implementierung der Quantenfehlerkorrektur jedoch einen erheblichen Mehraufwand im Hinblick auf die Anzahl der erforderlichen Qubits und niedrige Fehlerraten, die beide über die Möglichkeiten aktueller und künftiger Geräte hinausgehen.

Bis fehlertolerante Quantensimulationen möglich sind, verringern moderne Variationsalgorithmen den Bedarf an Quantenhardware erheblich und nutzen die Fähigkeiten verrauschter Quantengeräte mittlerer Größe.

Ein prominentes Beispiel ist der Variational Quantum Eigensolver (VQE), ein hybrider klassischer Quantenalgorithmus, der sich iterativ dem Minimum eines Ziel-Hamiltonoperators durch Variationsoptimierung einer Reihe parametrisierter Energieeigenwerte von Quantenschaltungen nähert. Neben anderen Variationsalgorithmen hat sich dies zu einer führenden Strategie entwickelt, um mithilfe moderner Geräte Quantenvorteile zu erzielen und den Fortschritt in mehreren Bereichen der Wissenschaft und Technologie zu beschleunigen.

Die experimentelle Implementierung von Variationsquantenalgorithmen bleibt für viele wissenschaftliche Probleme eine Herausforderung, da verrauschte Quantengeräte mittlerer Größe durch verschiedene Rauschquellen und Defekte beeinträchtigt werden. Derzeit wurden mehrere Quantum Error Mitigation (QEM)-Methoden zur Minderung dieser Probleme vorgeschlagen und experimentell verifiziert, wodurch das Quantencomputing ohne die für die Quantenfehlerkorrektur erforderlichen Quantenressourcen verbessert wird.

Typischerweise verwenden diese Methoden spezifische Informationen über Rauschkanäle, die sich auf die Quantenberechnung, die Hardware-Implementierung oder den Quantenalgorithmus selbst auswirken, einschließlich impliziter Darstellungen von Rauschmodellen und deren Auswirkungen auf Schätzungen erforderlicher Observablen, die in spezifischem Wissen über den Zustandsunterraum erstellt werden welche Quantenzustände vorhanden sein sollten und die Charakterisierung und Minderung von Rauschquellen auf verschiedenen Komponenten des Quantencomputings, wie z. B. Single-Qubit- und Two-Qubit-Gate-Fehler sowie Zustandsvorbereitungs- und Messfehler.

Techniken des maschinellen Lernens wurden kürzlich als Werkzeuge zur Lösung komplexer Probleme in der Quanten-Vielteilchenphysik und der Quanteninformationsverarbeitung umfunktioniert und bieten einen alternativen Ansatz zur QEM. Hier stellen Forscher der University of Waterloo eine QEM-Strategie namens Neural Error Mitigation (NEM) vor, die neuronale Netze nutzt, um Fehler bei der ungefähren Vorbereitung des Quantengrundzustands des Hamilton-Operators zu mildern.

Der NEM-Algorithmus besteht aus zwei Schritten. Zunächst führten die Forscher eine Neural Quantum State (NQS)-Tomographie (NQST) durch, um den NQS-Ansatz zu trainieren, um ungefähre Grundzustände darzustellen, die von verrauschten Quantengeräten mithilfe experimentell zugänglicher Messungen erstellt wurden. Inspiriert von der traditionellen Quantenzustandstomographie (QST) ist NQST eine datengesteuerte QST-Methode des maschinellen Lernens, die eine begrenzte Anzahl von Messungen verwendet, um komplexe Quantenzustände effizient zu rekonstruieren.

Dann wird ein Variations-Monte-Carlo-Algorithmus (VMC) auf denselben NQS-Ansatz (auch bekannt als NEM-Ansatz) angewendet, um die Darstellung des unbekannten Grundzustands zu verbessern. Ganz im Sinne von VQE approximiert VMC den Grundzustand des Hamilton-Operators basierend auf dem klassischen Variationsansatz, im Beispiel NQS-Ansatz.

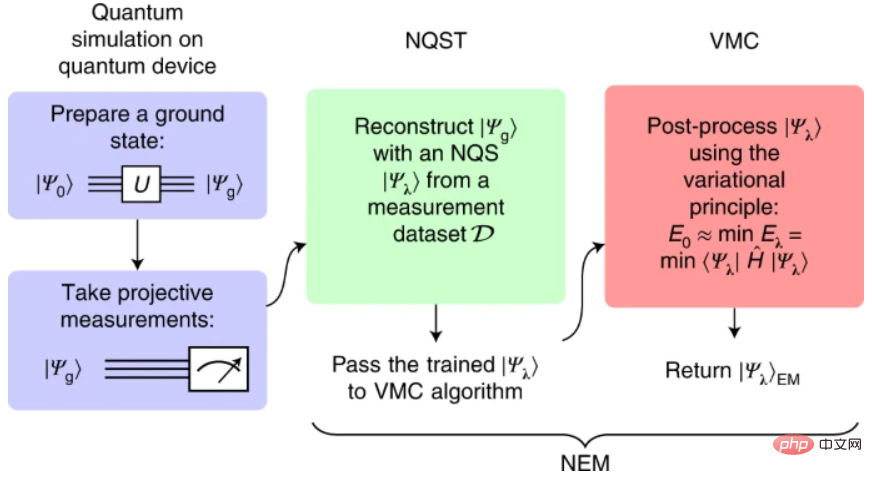
Abbildung: NEM-Programm. (Quelle: Paper)

Hier verwendeten die Forscher ein autoregressives generatives neuronales Netzwerk als NEM-Ansatz; genauer gesagt verwendeten sie die Transformer-Architektur und zeigten, dass das Modell als NQS gut funktionierte. Aufgrund ihrer Fähigkeit, zeitliche und räumliche Korrelationen über große Entfernungen zu simulieren, wurde diese Architektur in vielen hochmodernen Experimenten in den Bereichen natürliche Sprache und Bildverarbeitung eingesetzt und hat das Potenzial, Quantenkorrelationen über große Entfernungen zu simulieren .

NEM hat im Vergleich zu anderen Techniken zur Fehlerminderung mehrere Vorteile. Erstens ist der experimentelle Aufwand gering; es sind nur einfache experimentell durchführbare Messungen erforderlich, um die Eigenschaften der durch VQE vorbereiteten verrauschten Quantenzustände zu erlernen. Daher wird der Aufwand für die Fehlerminderung in NEM von Quantenressourcen (d. h. der Durchführung zusätzlicher Quantenexperimente und -messungen) auf klassische Rechenressourcen für maschinelles Lernen verlagert. Insbesondere stellten die Forscher fest, dass die Hauptkosten von NEM in der Durchführung von VMC vor der Konvergenz liegen. Ein weiterer Vorteil von NEM besteht darin, dass es unabhängig vom Quantensimulationsalgorithmus, dem Gerät, das ihn implementiert, und den spezifischen Rauschkanälen ist, die die Quantensimulation beeinflussen. Daher ist es auch mit anderen QEM-Techniken kombinierbar und kann zur Simulation quantenanaloger oder digitaler Quantenschaltkreise eingesetzt werden.

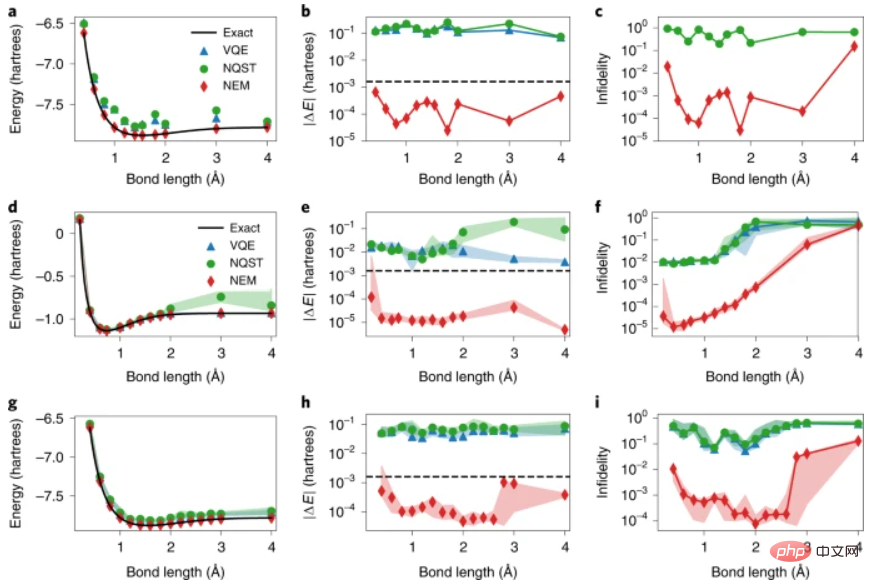Abbildung: experimentelle und numerische NEM-Ergebnisse des molekularen Hamiltonoperators. (Quelle: Paper)

NEM löst auch das Problem der geringen Messgenauigkeit, das bei der Schätzung von Quantenobservablen mit modernen Quantengeräten auftritt. Dies ist besonders wichtig bei Quantensimulationen, bei denen die genaue Schätzung von Quantenobservablen für praktische Anwendungen von entscheidender Bedeutung ist. NEM löst im Wesentlichen das Problem der geringen Messgenauigkeit bei jedem Schritt des Algorithmus. In einem ersten Schritt verbessert NQST die Varianz der beobachtbaren Schätzungen auf Kosten der Einführung einer kleinen Schätzungsverzerrung. Diese Verzerrung sowie die Restvarianz können durch das Training des NEM-Ansatzes mit VMC weiter reduziert werden, was dazu führt, dass die Energieschätzungen nach Erreichen des Grundzustands keine Varianz erwarten.

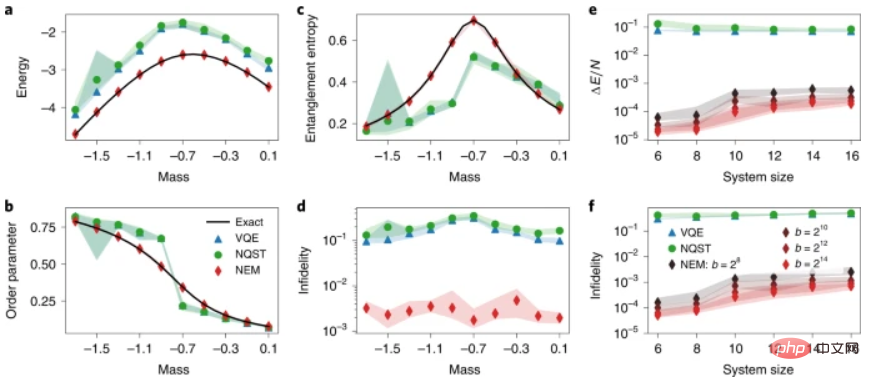Abbildung: Die Eigenschaften des NEM angewendet auf den Grundzustand des Gitter-Schwinger-Modells. (Quelle: Papier)

Durch die Kombination der Verwendung parametrischer Quantenschaltungen als VQE des Ansatzes und der Verwendung neuronaler Netze als NQST und VMC des Ansatzes kombiniert NEM zwei parametrische Quantenzustandsfamilien und drei Optimierungsprobleme bezüglich Ihre Verluste summierten sich. Die Forscher stellten Fragen zur Art der Beziehungen zwischen diesen Zustandsfamilien, ihren Verlusten und Quantenvorteilen. Die Untersuchung dieser Beziehungen bietet eine neue Möglichkeit, das Potenzial verrauschter Quantenalgorithmen mittlerer Größe bei der Suche nach Quantenvorteilen zu untersuchen. Dies könnte eine bessere Abgrenzung zwischen Simulationen klassisch beherrschbarer Quantensysteme und Simulationen, die Quantenressourcen erfordern, ermöglichen.

Link zum Papier: ​https://www.nature.com/articles/s42256-022-00509-0​

Ähnliche Berichte: ​https://techxplore.com/news/ 2022-08-neural-networkbased-strategy-near-term-quantum.html​

Das obige ist der detaillierte Inhalt vonEine auf einem neuronalen Netzwerk basierende Strategie zur Verbesserung von Quantensimulationen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!