18 Bilder zum intuitiven Verständnis neuronaler Netze, Mannigfaltigkeiten und Topologie

Eines der großen Bedenken bei neuronalen Netzen besteht bislang darin, dass es sich um Black Boxes handelt, die schwer zu erklären sind. In diesem Artikel wird hauptsächlich theoretisch verstanden, warum neuronale Netze bei der Mustererkennung und -klassifizierung so effektiv sind. Ihr Kern besteht darin, die ursprüngliche Eingabe durch Schichten affiner Transformation und nichtlinearer Transformation zu verzerren und zu verformen, bis sie leicht in verschiedene Kategorien unterschieden werden kann. Tatsächlich passt der Backpropagation-Algorithmus (BP) den Verzerrungseffekt kontinuierlich auf der Grundlage der Trainingsdaten an.

Seit etwa zehn Jahren haben tiefe neuronale Netze bahnbrechende Ergebnisse in Bereichen wie Computer Vision erzielt und großes Interesse und Aufmerksamkeit geweckt.

Einige Menschen sind jedoch immer noch besorgt darüber. Ein Grund dafür ist, dass ein neuronales Netzwerk eine Black Box ist: Wenn ein neuronales Netzwerk gut trainiert wird, können qualitativ hochwertige Ergebnisse erzielt werden, es ist jedoch schwierig zu verstehen, wie es funktioniert. Bei einer Fehlfunktion eines neuronalen Netzwerks kann es schwierig sein, das Problem genau zu lokalisieren.

Obwohl es schwierig ist, tiefe neuronale Netze als Ganzes zu verstehen, können Sie mit niedrigdimensionalen tiefen neuronalen Netzen beginnen, also Netzen mit nur wenigen Neuronen in jeder Schicht, die viel einfacher zu verstehen sind. Durch Visualisierungsmethoden können wir das Verhalten und Training niedrigdimensionaler tiefer neuronaler Netze verstehen. Mithilfe von Visualisierungsmethoden können wir das Verhalten neuronaler Netze intuitiver verstehen und den Zusammenhang zwischen neuronalen Netzen und Topologie beobachten.

Als nächstes werde ich über viele interessante Dinge sprechen, einschließlich der Untergrenze der Komplexität eines neuronalen Netzwerks, das einen bestimmten Datensatz klassifizieren kann.

1. Ein einfaches Beispiel

Lassen Sie uns mit einem sehr einfachen Datensatz beginnen. In der Abbildung unten bestehen zwei Kurven in der Ebene aus unzähligen Punkten. Das neuronale Netzwerk versucht zu unterscheiden, zu welcher Linie diese Punkte gehören.

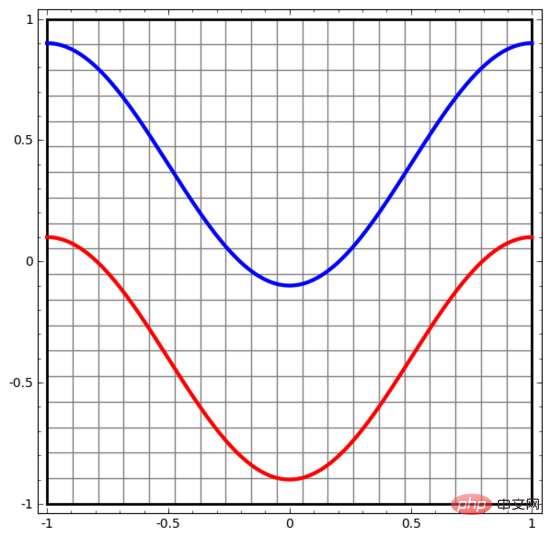
Der einfachste Weg, das Verhalten eines neuronalen Netzwerks (oder eines beliebigen Klassifizierungsalgorithmus) zu beobachten, besteht darin, zu sehen, wie es jeden Datenpunkt klassifiziert.

Wir beginnen mit dem einfachsten neuronalen Netzwerk, das nur eine Eingabeschicht und eine Ausgabeschicht hat. Ein solches neuronales Netzwerk trennt einfach zwei Arten von Datenpunkten durch eine gerade Linie.

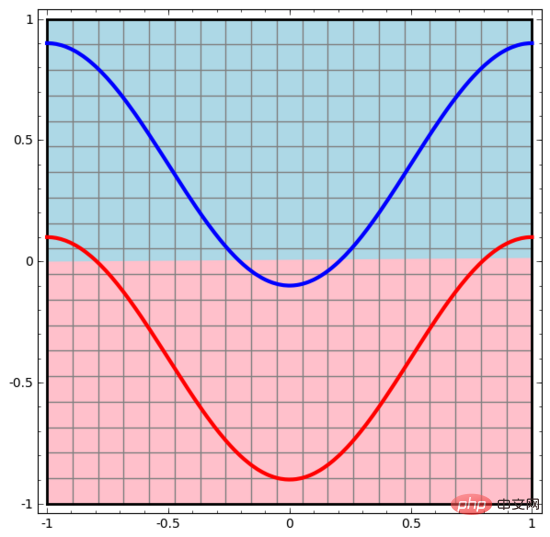
Ein solches neuronales Netzwerk ist zu einfach und grob. Moderne neuronale Netze verfügen oft über mehrere Schichten zwischen der Eingabe- und Ausgabeschicht, sogenannte versteckte Schichten. Selbst das einfachste moderne neuronale Netzwerk verfügt über mindestens eine verborgene Schicht.

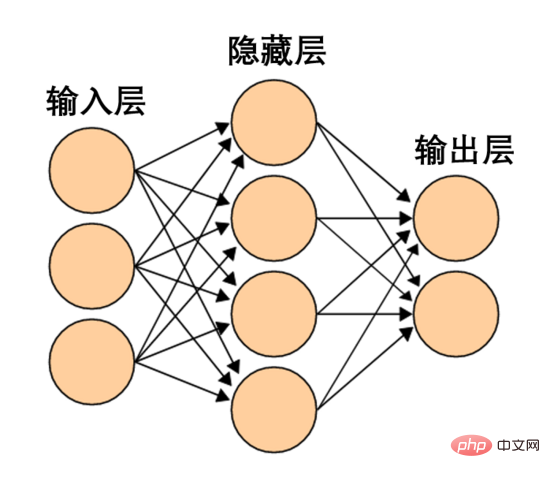
Ein einfaches neuronales Netzwerk, Bildquelle Wikipedia

Ähnlich beobachten wir, was das neuronale Netzwerk für jeden Datenpunkt tut. Wie man sehen kann, verwendet dieses neuronale Netzwerk eine Kurve anstelle einer geraden Linie, um Datenpunkte zu trennen. Offensichtlich sind Kurven komplexer als gerade Linien.

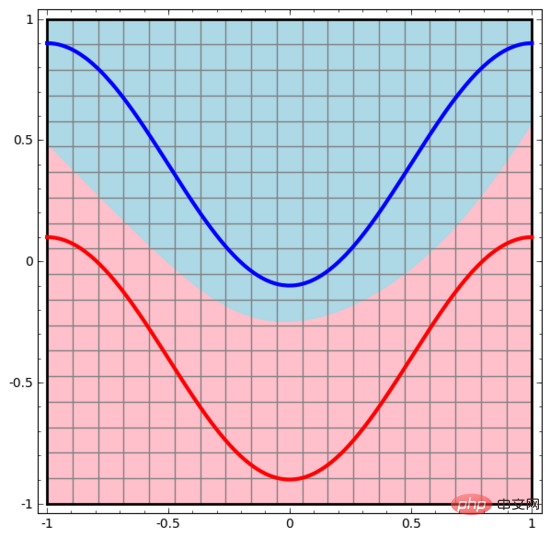
Jede Schicht des neuronalen Netzwerks verwendet eine neue Darstellung, um die Daten darzustellen. Wir können beobachten, wie die Daten in neue Darstellungen umgewandelt werden und wie das neuronale Netzwerk sie klassifiziert. In der letzten Darstellungsebene zeichnet das neuronale Netzwerk eine Linie zwischen den beiden Datentypen (oder eine Hyperebene, wenn es sich um höhere Dimensionen handelt).

In der vorherigen Visualisierung haben wir die Originaldarstellung der Daten gesehen. Man kann sich das so vorstellen, wie die Daten in der „Eingabeebene“ aussehen. Schauen wir uns nun an, wie die Daten nach der Transformation aussehen. Sie können sich vorstellen, wie die Daten in der „verborgenen Ebene“ aussehen.

Jede Dimension der Daten entspricht der Aktivierung eines Neurons in der neuronalen Netzwerkschicht.

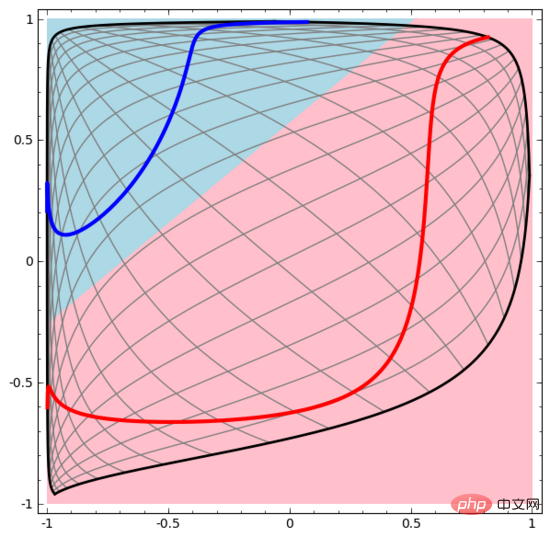
Die verborgene Ebene verwendet die obige Methode zur Darstellung der Daten, sodass die Daten durch eine gerade Linie (dh linear trennbar) getrennt werden können

2. Kontinuierliche Visualisierung von Ebenen

In der Methode in Im vorherigen Abschnitt stellt jede Schicht des neuronalen Netzwerks Daten in unterschiedlichen Darstellungen dar. Auf diese Weise sind die Darstellungen jeder Schicht diskret und nicht kontinuierlich.

Dies führt zu Verständnisschwierigkeiten. Wie kann man von einer Darstellung in eine andere konvertieren? Glücklicherweise ist dieser Aspekt aufgrund der Eigenschaften der neuronalen Netzwerkschicht sehr einfach zu verstehen.

In neuronalen Netzen gibt es verschiedene Schichten. Im Folgenden werden wir die Tanh-Schicht als konkretes Beispiel diskutieren. Eine Tanh-Schicht, einschließlich:

• Verwenden Sie die „Gewichts“-Matrix W für die lineare Transformation.
• Verwenden Sie den Vektor b für die Übersetzung.
• Verwenden Sie tanh, um Punkt für Punkt darzustellen.

Wir können es uns wie folgt als kontinuierliche Transformation vorstellen :

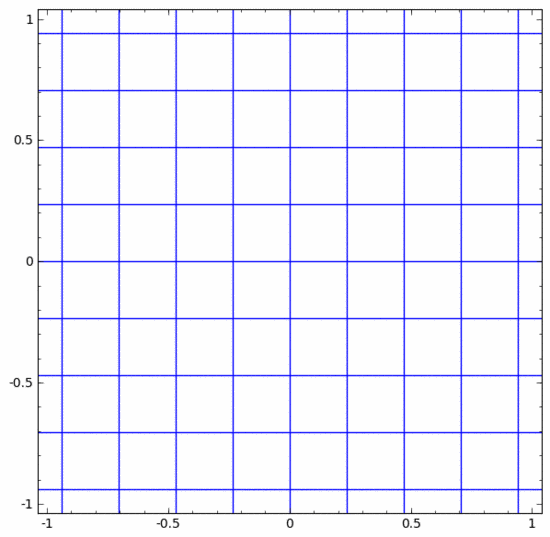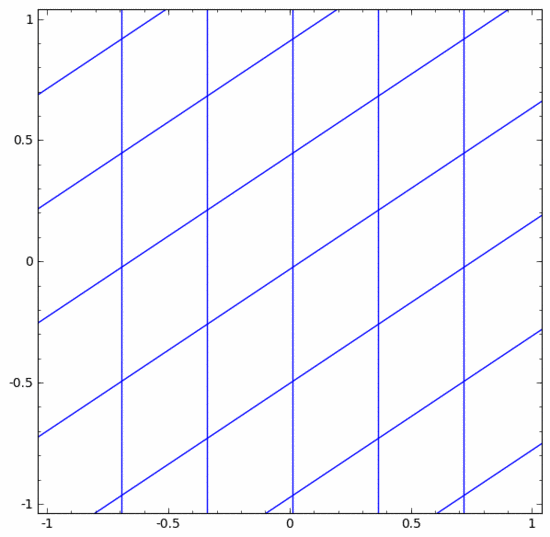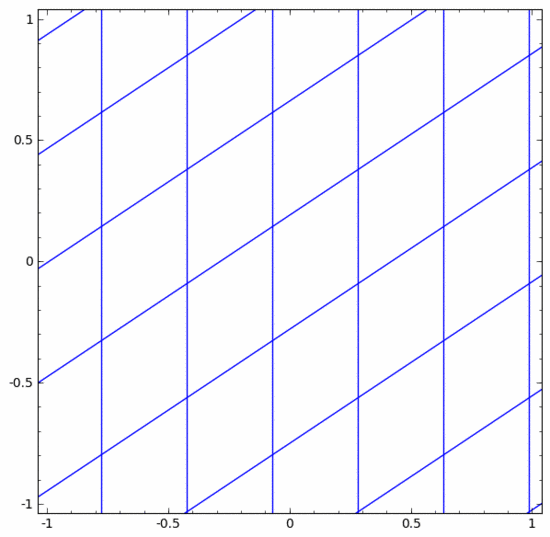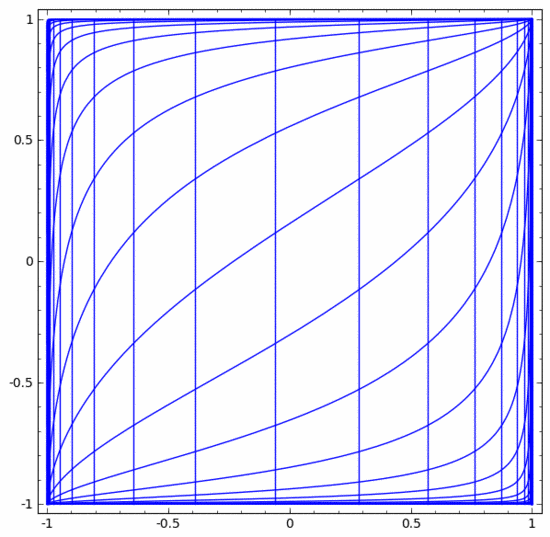
Andere Standardebenen sind weitgehend gleich und bestehen aus der punktuellen Anwendung affiner Transformationen und monotoner Aktivierungsfunktionen.

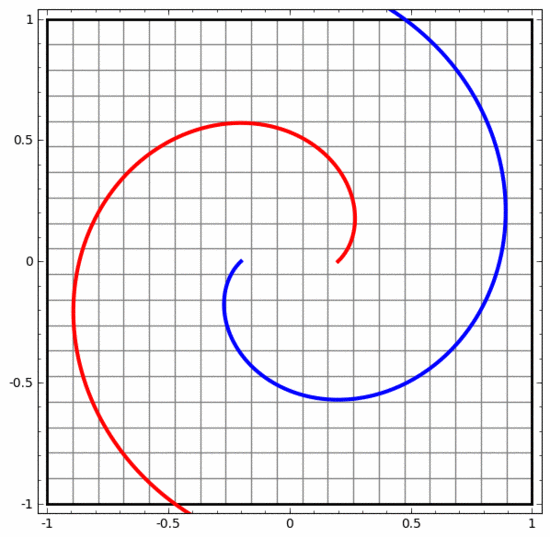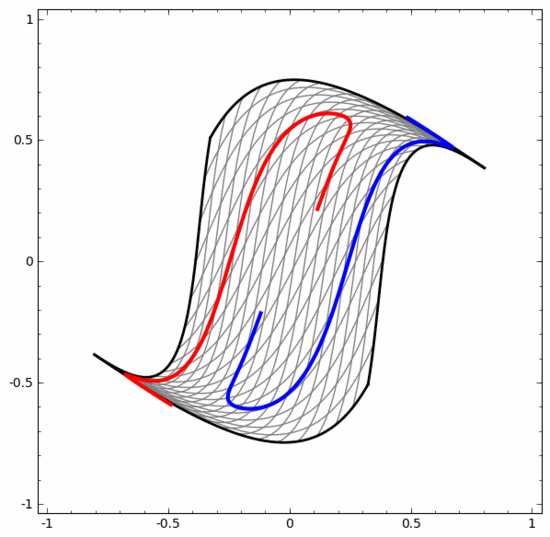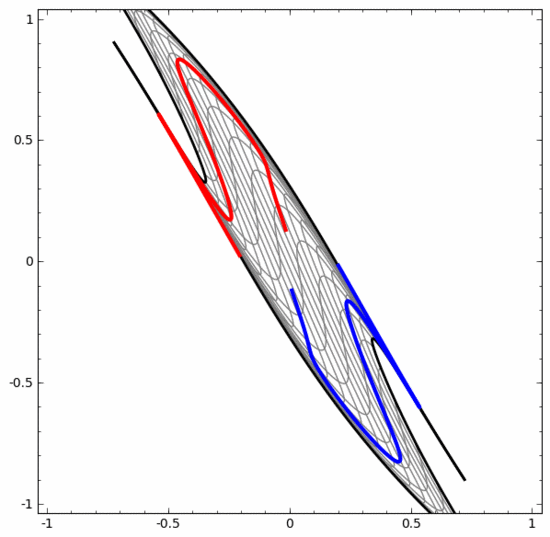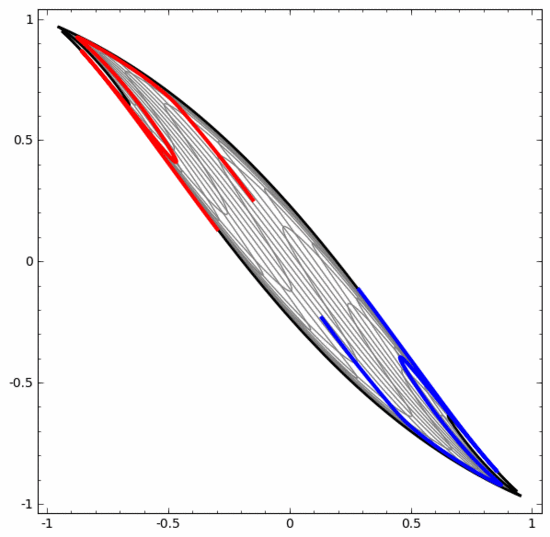
Mit dieser Methode können wir komplexere neuronale Netze verstehen. Das folgende neuronale Netzwerk verwendet beispielsweise vier verborgene Schichten, um zwei leicht ineinander verschlungene Spiralen zu klassifizieren. Es ist ersichtlich, dass zur Klassifizierung der Daten die Darstellung der Daten kontinuierlich transformiert wird. Die beiden Spiralen sind zunächst verschränkt, können aber schließlich durch eine gerade Linie getrennt werden (linear trennbar).

Obwohl das folgende neuronale Netzwerk auch mehrere verborgene Schichten verwendet, kann es andererseits nicht zwei Spiralen teilen, die tiefer miteinander verflochten sind.

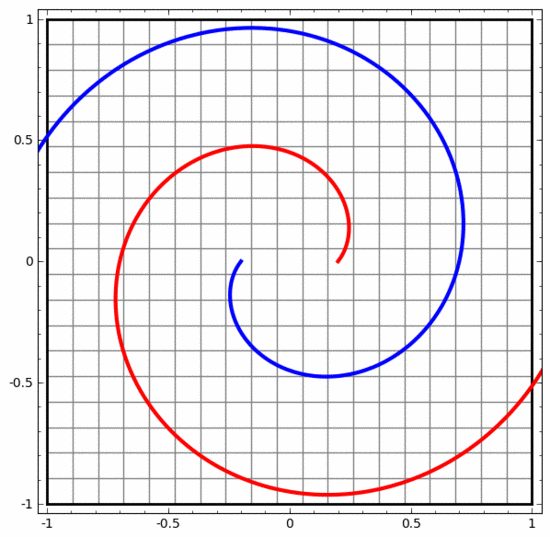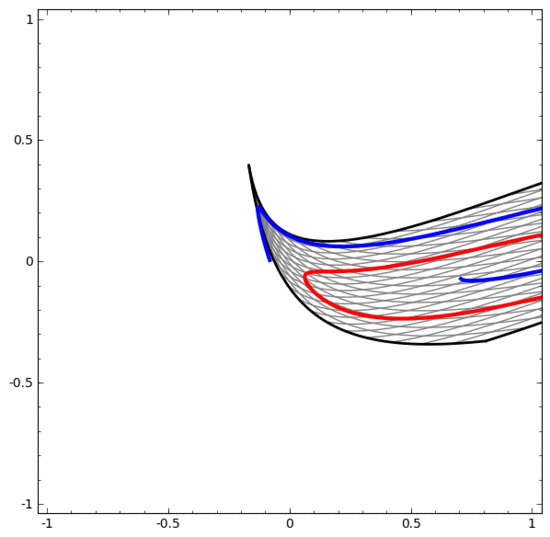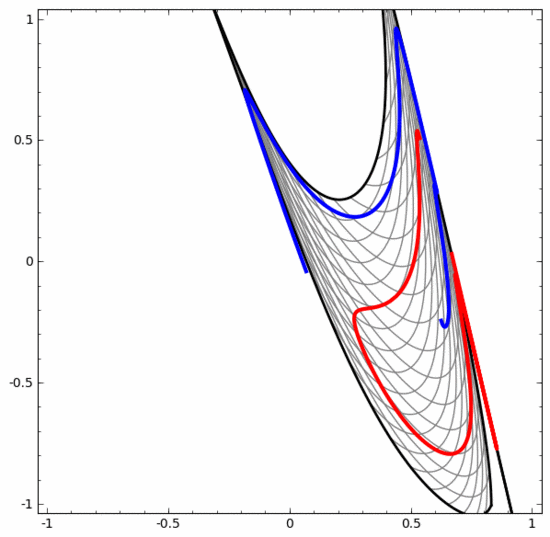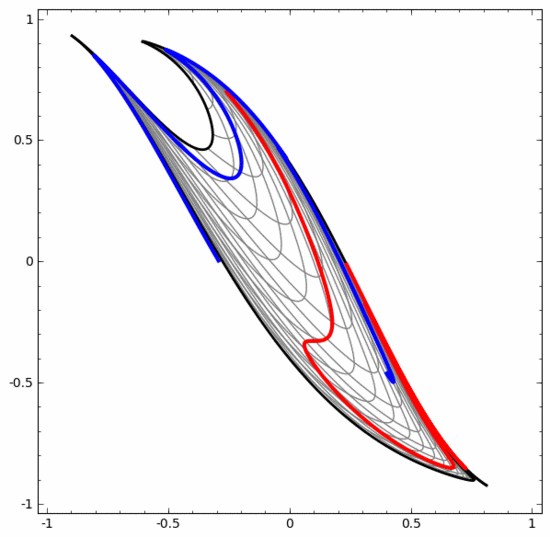
Es sollte klar darauf hingewiesen werden, dass die beiden oben genannten Spiralklassifizierungsaufgaben einige Herausforderungen mit sich bringen, da wir derzeit nur niedrigdimensionale neuronale Netze verwenden. Alles wäre viel einfacher, wenn wir ein breiteres neuronales Netzwerk verwenden würden.

(Andrej Karpathy hat eine gute Demo basierend auf ConvnetJS erstellt, die es Menschen ermöglicht, das neuronale Netzwerk durch diese Art von visuellem Training interaktiv zu erkunden.)

3. Topologie der Tanh-Schicht

Jede Schicht des neuronalen Netzwerks wird gedehnt und quetscht den Raum, aber es schneidet, spaltet oder faltet ihn nicht. Intuitiv zerstören neuronale Netze nicht die topologischen Eigenschaften der Daten. Wenn beispielsweise ein Datensatz kontinuierlich ist, ist auch seine transformierte Darstellung kontinuierlich (und umgekehrt).

Transformationen wie diese, die die topologischen Eigenschaften nicht beeinflussen, werden Homöomorphismen genannt. Formal sind sie Bijektionen bidirektionaler stetiger Funktionen.

Theorem: Wenn die Gewichtsmatrix W nicht singulär ist und eine Schicht des neuronalen Netzwerks N Eingänge und N Ausgänge hat, dann ist die Abbildung dieser Schicht homöomorph (für einen bestimmten Bereich und Wertebereich). Wort).

Beweis: Gehen wir Schritt für Schritt vor:

1. Nehmen Sie an, dass W eine Determinante ungleich Null hat. Dann handelt es sich um eine bilineare lineare Funktion mit einer linearen Umkehrung. Lineare Funktionen sind stetig. Dann ist die Transformation wie „Multiplikation mit W“ Homöomorphismus;

3 (auch Sigmoid und Softplus) ist eine kontinuierliche Funktion. (für einen bestimmten Bereich und Bereich) sind sie Bijektionen und ihre punktweise Anwendung ist Homöomorphismus.

Wenn es also eine Determinante ungleich Null von W gibt, ist diese neuronale Netzwerkschicht homöomorph.

Wenn wir solche Schichten zufällig miteinander kombinieren, gilt dieses Ergebnis immer noch.

4. Topologie und Klassifizierung

Sehen wir uns einen zweidimensionalen Datensatz an, der zwei Arten von Daten A und B enthält:

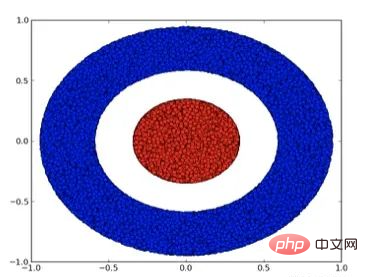A ist rot, B ist blau

Erklärung: Zum Verständnis Damit ein Datensatz klassifiziert werden kann, muss ein neuronales Netzwerk (unabhängig von der Tiefe) eine Schicht mit 3 oder mehr versteckten Einheiten haben.

Wie bereits erwähnt, entspricht die Verwendung von Sigmoideinheiten oder Softmax-Ebenen zur Klassifizierung dem Finden einer Hyperebene (in diesem Fall einer geraden Linie) in der Darstellung der letzten Ebene, um A und B zu trennen. Mit nur zwei versteckten Einheiten ist das neuronale Netz topologisch nicht in der Lage, die Daten auf diese Weise zu trennen und somit den obigen Datensatz nicht zu klassifizieren.

In der folgenden Visualisierung transformiert die verborgene Ebene die Darstellung der Daten, mit geraden Linien als Trennlinien. Es ist ersichtlich, dass sich die Trennlinie weiterhin dreht und bewegt, die beiden Datentypen A und B jedoch nie gut trennen können.

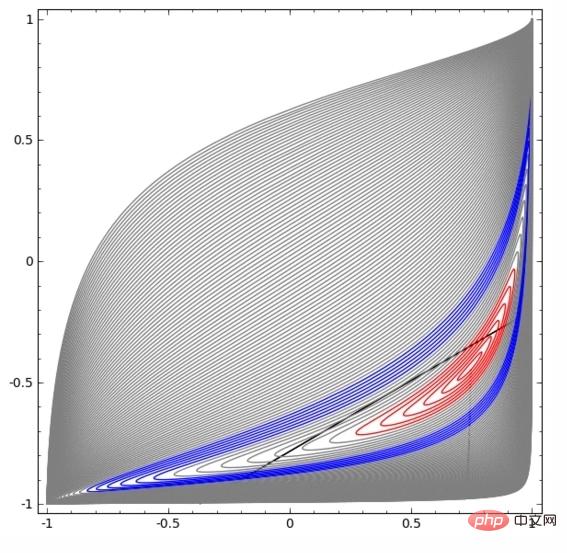Egal wie gut ein neuronales Netzwerk trainiert ist, es kann die Klassifizierungsaufgabe nicht gut lösen

Am Ende kann es nur knapp ein lokales Minimum erreichen und eine Klassifizierungsgenauigkeit von 80 % erreichen.

Das obige Beispiel hat nur eine ausgeblendete Ebene, und da es nur zwei ausgeblendete Einheiten gibt, kann die Klassifizierung ohnehin nicht durchgeführt werden.

Beweis: Wenn es nur zwei versteckte Einheiten gibt, ist entweder die Transformation dieser Schicht homöomorph oder die Gewichtsmatrix der Schicht hat die Determinante 0. Wenn es sich um einen Homöomorphismus handelt, ist A immer noch von B umgeben und A und B können nicht durch eine gerade Linie getrennt werden. Wenn es eine Determinante von 0 gibt, wird der Datensatz auf einer Achse reduziert. Da A von B umgeben ist, führt die Faltung von A auf einer beliebigen Achse dazu, dass einige der A-Datenpunkte mit B vermischt werden, wodurch es unmöglich wird, A von B zu unterscheiden.

Aber wenn wir eine dritte versteckte Einheit hinzufügen, ist das Problem gelöst. Zu diesem Zeitpunkt kann das neuronale Netzwerk die Daten in die folgende Darstellung umwandeln:

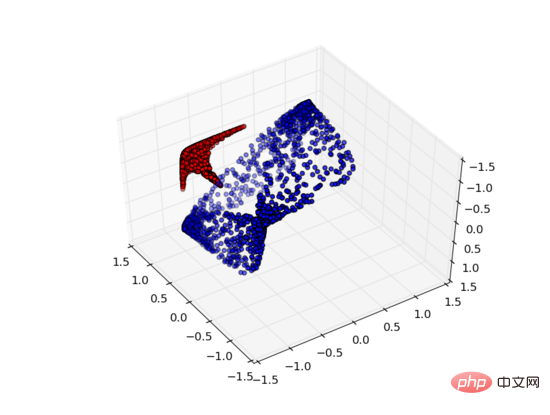
Zu diesem Zeitpunkt kann eine Hyperebene verwendet werden, um A und B zu trennen.

Um sein Prinzip besser zu erklären, hier ein einfacherer eindimensionaler Datensatz als Beispiel:

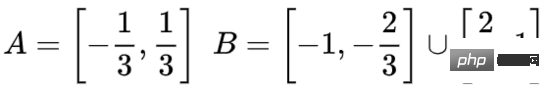
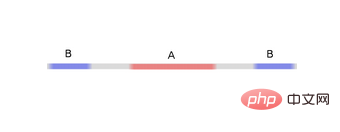
Um diesen Datensatz zu klassifizieren, müssen Sie eine verborgene Einheit verwenden, die aus zwei oder mehr verborgenen Einheiten besteht. Wenn Sie zwei versteckte Einheiten verwenden, können Sie eine schöne Kurve zur Darstellung der Daten verwenden, sodass Sie A und B durch eine gerade Linie trennen können:

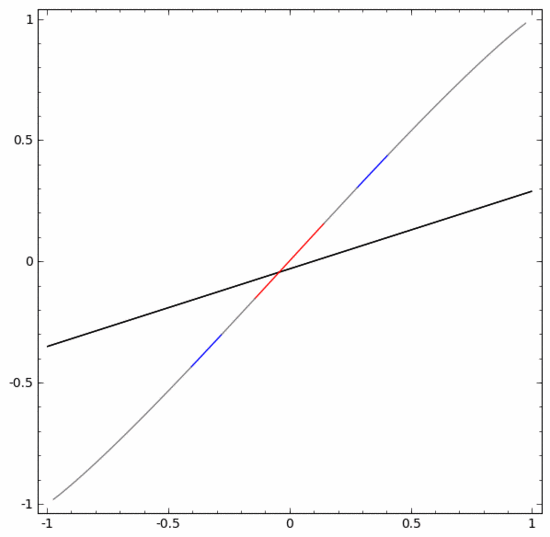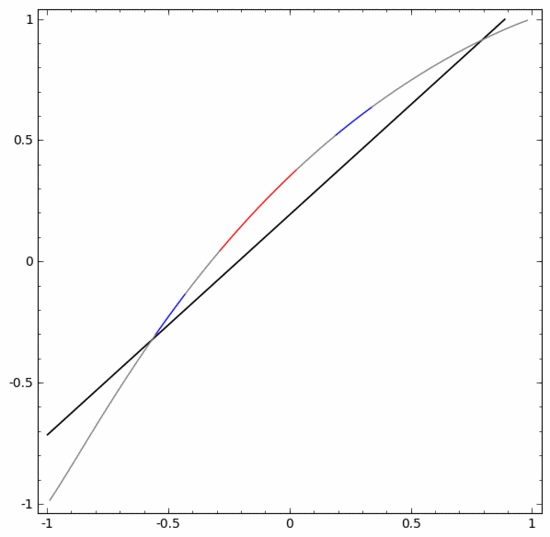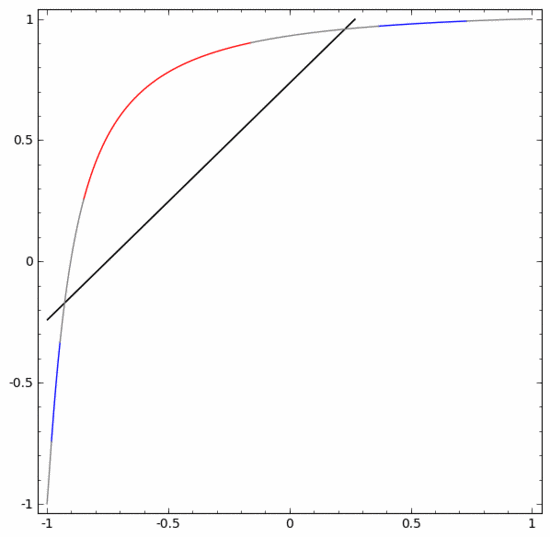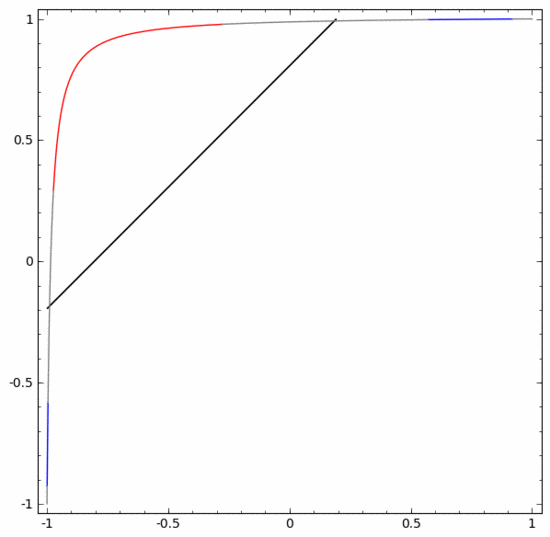
Wie wird das gemacht? Wenn , wird eine der versteckten Einheiten aktiviert; wenn 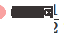, wird die andere versteckte Einheit aktiviert. Wenn die vorherige verborgene Einheit aktiviert ist und die nächste verborgene Einheit nicht aktiviert ist, kann festgestellt werden, dass es sich um einen Datenpunkt handelt, der zu A gehört.

5. Mannigfaltigkeitshypothese

Ist die Mannigfaltigkeitshypothese für die Verarbeitung realer Datensätze (z. B. Bilddaten) sinnvoll? Ich denke, es macht Sinn.

Die Mannigfaltigkeitshypothese bedeutet, dass natürliche Daten in ihrem Einbettungsraum eine niedrigdimensionale Mannigfaltigkeit bilden. Diese Hypothese hat theoretische und experimentelle Unterstützung. Wenn Sie an die Mannigfaltigkeitshypothese glauben, besteht die Aufgabe eines Klassifizierungsalgorithmus darin, eine Menge verschränkter Mannigfaltigkeiten zu trennen.

Im vorherigen Beispiel umgab eine Klasse die andere Klasse vollständig. In realen Daten ist es jedoch unwahrscheinlich, dass die Bildmannigfaltigkeit des Hundes vollständig von der Bildmannigfaltigkeit der Katze umgeben ist. Andere, vernünftigere topologische Situationen können jedoch immer noch Probleme verursachen, wie im nächsten Abschnitt erläutert wird.

6. Links und Homotopie

Jetzt werde ich über einen weiteren interessanten Datensatz sprechen: zwei verknüpfte Torus (Tori), A und B.

Ähnlich wie bei der Datensatzsituation, über die wir zuvor gesprochen haben, können Sie einen n-dimensionalen Datensatz nicht trennen, ohne die n+1-Dimension zu verwenden (die n+1-Dimension ist in diesem Beispiel die 4. Dimension).

Das Verbindungsproblem gehört zur Knotentheorie in der Topologie. Wenn wir eine Verbindung sehen, können wir manchmal nicht sofort erkennen, ob es sich um eine defekte Verbindung handelt (unlink bedeutet, dass sie, obwohl sie miteinander verwickelt sind, durch kontinuierliche Verformung getrennt werden können).

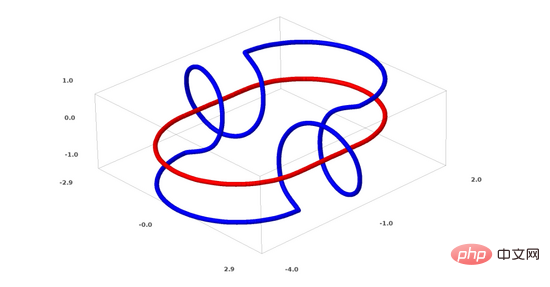
Ein einfacherer defekter Link

Wenn ein neuronales Netzwerk mit nur 3 versteckten Einheiten in der verborgenen Schicht einen Datensatz klassifizieren kann, dann ist dieser Datensatz ein defekter Link (das Problem ist: Theoretisch können alle defekten Links sein klassifiziert durch ein neuronales Netzwerk mit nur 3 versteckten Einheiten?

Aus Sicht der Knotentheorie ist die kontinuierliche Visualisierung von Datendarstellungen, die von neuronalen Netzen erzeugt werden, nicht nur eine schöne Animation, sondern auch ein Prozess, bei dem Verknüpfungen aufgelöst werden. In der Topologie nennen wir dies die Umgebungsisotopie zwischen der ursprünglichen Verbindung und der getrennten Verbindung.

Der umgebende Homomorphismus zwischen Mannigfaltigkeit A und Mannigfaltigkeit B ist eine stetige Funktion:

Jeder ist ein Homöomorphismus von X. ist die charakteristische Funktion, die A auf B abbildet. Das heißt, der ständige Übergang von der Zuordnung von A zu sich selbst zur Zuordnung von A zu B.

Satz: Wenn die folgenden drei Bedingungen gleichzeitig erfüllt sind: (1) W ist nicht singulär; (2) die Reihenfolge der Neuronen in der verborgenen Schicht kann manuell angeordnet werden; (3) die Anzahl der verborgenen Einheiten ist größer als 1, dann gibt es zwischen den Eingaben des neuronalen Netzwerks und dem neuronalen Netzwerk eine umlaufende Spur zwischen den von der Netzwerkschicht erzeugten Darstellungen.

Beweis: Wir gehen auch Schritt für Schritt vor:

1 Der schwierigste Teil ist die lineare Transformation. Um eine lineare Transformation zu erreichen, benötigen wir eine positive Determinante von W. Unsere Prämisse ist, dass die Determinante ungleich Null ist. Wenn die Determinante negativ ist, können wir sie durch den Austausch zweier verborgener Neuronen ins Positive umwandeln. Der Raum der positiven Determinantenmatrix ist pfadverbunden, es gibt also 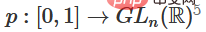, also 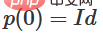, 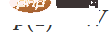. Mit der Funktion 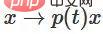können wir die Eigenfunktion kontinuierlich in die W-Transformation überführen, indem wir x mit der Matrix des kontinuierlichen Übergangs an jedem Punkt zum Zeitpunkt t multiplizieren.

2. Sie können über die Funktion 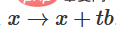von der charakteristischen Funktion zur b-Übersetzung übergehen.

3. Sie können über die Funktion 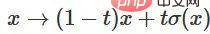von der charakteristischen Funktion zur Punkt-für-Punkt-Anwendung übergehen.

Ich vermute, dass jemand an der folgenden Frage interessiert sein könnte: Kann ein Programm entwickelt werden, das solche Umgebungsisotopien automatisch erkennen und auch automatisch die Äquivalenz einiger verschiedener Verbindungen oder die Trennbarkeit einiger Verbindungen beweisen kann? Ich möchte auch wissen, ob neuronale Netze in dieser Hinsicht die aktuelle SOTA-Technologie schlagen können.

Obwohl die Form der Verknüpfung, über die wir jetzt sprechen, wahrscheinlich nicht in realen Daten vorkommen wird, kann es in realen Daten zu höherdimensionalen Verallgemeinerungen kommen.

Links und Knoten sind beide eindimensionale Mannigfaltigkeiten, es werden jedoch 4 Dimensionen benötigt, um sie zu trennen. Ebenso ist zur Trennung einer n-dimensionalen Mannigfaltigkeit ein höherdimensionaler Raum erforderlich. Alle n-dimensionalen Mannigfaltigkeiten können in 2n+2 Dimensionen zerlegt werden.

7. Eine einfache Methode

Für neuronale Netze besteht die einfachste Methode darin, die ineinander verschlungenen Mannigfaltigkeiten direkt auseinanderzuziehen und diese verschlungenen Teile so dünn wie möglich zu machen. Obwohl dies nicht die grundlegende Lösung ist, die wir verfolgen, kann damit eine relativ hohe Klassifizierungsgenauigkeit und ein relativ ideales lokales Minimum erreicht werden.

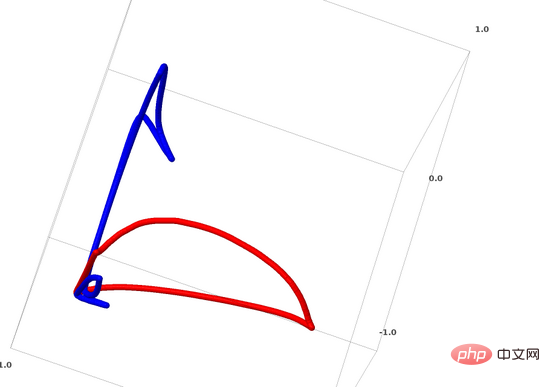
Dieser Ansatz führt zu sehr hohen Ableitungen in dem Bereich, den Sie dehnen möchten. Um damit umzugehen, müssen Sie eine Schrumpfungsstrafe verwenden, die die Ableitung der Datenpunktebene bestraft.

Lokale Minima sind für die Lösung topologischer Probleme nicht nützlich, aber topologische Probleme können gute Ideen für die Erforschung und Lösung der oben genannten Probleme liefern.

Wenn es uns andererseits nur darum geht, gute Klassifizierungsergebnisse zu erzielen, ist es dann ein Problem für uns, wenn ein kleiner Teil der Mannigfaltigkeit mit einer anderen Mannigfaltigkeit verwickelt ist? Wenn wir uns nur um die Klassifizierungsergebnisse kümmern, scheint dies kein Problem zu sein.

(Meine Intuition ist, dass solche Abkürzungen nicht gut sind und leicht in eine Sackgasse führen können. Insbesondere bei Optimierungsproblemen löst die Suche nach einem lokalen Minimum das Problem nicht wirklich, und wenn man ein lokales Minimum wählt, löst das schon Das Problem wird nicht wirklich gelöst. Die Lösung wird letztendlich keine gute Leistung erzielen)

8. Wählen Sie eine neuronale Netzwerkschicht, die für vielfältige Manipulationen besser geeignet ist?

Ich denke, dass Standardschichten neuronaler Netzwerke nicht für die Manipulation von Mannigfaltigkeiten geeignet sind, da sie affine Transformationen und punktweise Aktivierungsfunktionen verwenden.

Vielleicht können wir eine völlig andere neuronale Netzwerkschicht verwenden?

Eine Idee, die mir in den Sinn kommt, ist, das neuronale Netzwerk zunächst ein Vektorfeld lernen zu lassen, dessen Richtung die Richtung ist, in die wir die Mannigfaltigkeit verschieben möchten:

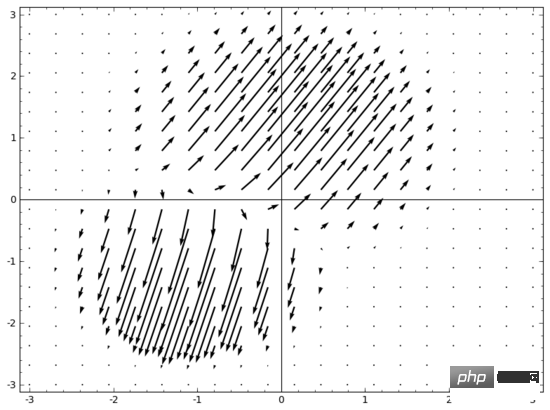
, und dann den Raum auf dieser Grundlage zu verformen:

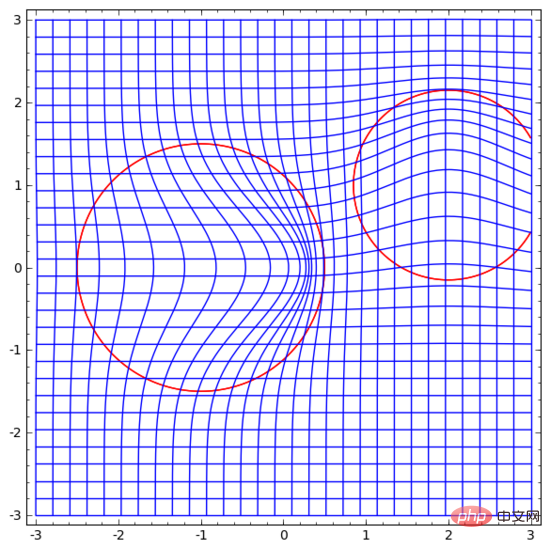
Wir können Vektorfelder an festen Punkten lernen (wählen Sie einfach einige feste Punkte aus dem Trainingssatz als Anker aus) und sie irgendwie interpolieren. Das obige Vektorfeld hat die Form:

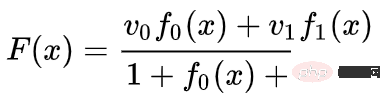
wobei und Vektoren und n-dimensionale Gaußsche Funktionen sind. Diese Idee ist von radialen Basisfunktionen inspiriert.

9. K-Nearest Neighbor Layer

Mein anderer Punkt ist, dass die lineare Trennbarkeit eine übermäßige und unangemessene Anforderung für neuronale Netze sein kann. Vielleicht wäre es besser, k-Nearest Neighbor (k-NN) zu verwenden. Der k-NN-Algorithmus ist jedoch stark auf die Darstellung von Daten angewiesen. Daher ist eine gute Datendarstellung erforderlich, damit der k-NN-Algorithmus gute Ergebnisse erzielt.

Im ersten Experiment habe ich einige MNIST-Neuronale Netze (zweischichtiges CNN, kein Dropout) mit einer Fehlerrate unter 1 % trainiert. Dann habe ich die letzte Softmax-Schicht verworfen und den k-NN-Algorithmus verwendet, und die Ergebnisse zeigten mehrfach, dass die Fehlerrate um 0,1–0,2 % reduziert wurde.

Allerdings habe ich das Gefühl, dass dieser Ansatz immer noch falsch ist. Das neuronale Netzwerk versucht immer noch, linear zu klassifizieren, aber da es den k-NN-Algorithmus verwendet, kann es einige der Fehler, die es macht, leicht korrigieren und dadurch die Fehlerrate reduzieren.

Aufgrund der (1/Distanz)-Gewichtung ist k-NN von der Datendarstellung, auf die es einwirkt, differenzierbar. Daher können wir das neuronale Netzwerk direkt für die k-NN-Klassifizierung trainieren. Dies kann man sich als „Nearest Neighbor“-Schicht vorstellen, die sich ähnlich wie eine Softmax-Schicht verhält.

Wir möchten nicht den gesamten Trainingssatz für jeden Mini-Batch zurückmelden, da dies zu rechenintensiv ist. Ich denke, ein guter Ansatz wäre, jedes Element im Mini-Batch basierend auf der Kategorie der anderen Elemente im Mini-Batch zu klassifizieren und jedem Element eine Gewichtung von (1/(Abstand vom Klassifizierungsziel)) zu geben.

Leider kann selbst bei komplexen Architekturen die Verwendung des k-NN-Algorithmus die Fehlerrate nur auf 4-5 % reduzieren, während bei einfachen Architekturen die Fehlerrate höher ist. Allerdings habe ich mir nicht viel Mühe mit den Hyperparametern gegeben.

Aber mir gefällt der k-NN-Algorithmus trotzdem, weil er besser für neuronale Netze geeignet ist. Wir möchten, dass Punkte auf derselben Mannigfaltigkeit näher beieinander liegen, anstatt darauf zu bestehen, Hyperebenen zu verwenden, um die Mannigfaltigkeiten zu trennen. Dies läuft darauf hinaus, eine einzelne Mannigfaltigkeit zu verkleinern und gleichzeitig den Raum zwischen Mannigfaltigkeiten verschiedener Kategorien zu vergrößern. Dies vereinfacht das Problem.

10. Zusammenfassung

Einige topologische Eigenschaften der Daten können dazu führen, dass diese Daten mithilfe niedrigdimensionaler neuronaler Netze nicht linear getrennt werden können (unabhängig von der Tiefe des neuronalen Netzes). Selbst dort, wo es technisch machbar ist, wie etwa bei Spiralen, ist die Trennung mit niedrigdimensionalen neuronalen Netzen nur sehr schwer zu erreichen.

Um Daten genau zu klassifizieren, erfordern neuronale Netze manchmal breitere Schichten. Darüber hinaus eignen sich herkömmliche neuronale Netzwerkschichten nicht zur Manipulation von Mannigfaltigkeiten. Selbst wenn die Gewichte manuell festgelegt werden, ist es schwierig, eine ideale Datentransformationsdarstellung zu erhalten. Neue Schichten neuronaler Netze können möglicherweise eine gute unterstützende Rolle spielen, insbesondere neue Schichten neuronaler Netze, die durch das Verständnis maschinellen Lernens aus einer vielfältigen Perspektive inspiriert sind.

Das obige ist der detaillierte Inhalt von18 Bilder zum intuitiven Verständnis neuronaler Netze, Mannigfaltigkeiten und Topologie. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!