Heim >Technologie-Peripheriegeräte >KI >Regressions-Meta-Lernen, Zielerkennung mit wenigen Stichproben basierend auf der Aggregation von Variationsmerkmalen, um neue SOTA zu erreichen
Regressions-Meta-Lernen, Zielerkennung mit wenigen Stichproben basierend auf der Aggregation von Variationsmerkmalen, um neue SOTA zu erreichen
- WBOYnach vorne
- 2023-04-12 18:46:03893Durchsuche
Im Gegensatz zu herkömmlichen Objekterkennungsproblemen geht die Wenig-Schuss-Objekterkennung (FSOD) davon aus, dass wir über viele Basisklassenbeispiele, aber nur eine kleine Anzahl neuartiger Klassenbeispiele verfügen. Ziel ist es, zu untersuchen, wie Wissen von Grundklassen auf neuartige Klassen übertragen werden kann, um so die Fähigkeit des Detektors zu verbessern, neuartige Klassen zu erkennen.
FSOD folgt in der Regel einem zweistufigen Trainingsparadigma . In der ersten Phase wird der Detektor mithilfe umfangreicher Basisklassenproben trainiert, um allgemeine Darstellungen zu erlernen, die für Objekterkennungsaufgaben wie Objektlokalisierung und -klassifizierung erforderlich sind. In der zweiten Stufe erfolgt die Feinabstimmung des Detektors unter Verwendung nur einer kleinen Anzahl (z. B. 1, 2, 3 ...) von Proben neuer Klassen. Aufgrund des Ungleichgewichts in der Anzahl der Basisklassen- und neuartigen Klassenstichproben ist das erlernte Modell jedoch normalerweise auf die Basisklasse ausgerichtet, was zu einer Verwechslung von neuartigen Klassenzielen mit ähnlichen Basisklassen führt. Da es für jede neuartige Klasse nur wenige Stichproben gibt, reagiert das Modell außerdem empfindlich auf die Varianz der neuartigen Klassen. Wenn Sie beispielsweise für mehrere Schulungen zufällig Stichproben aus neuartigen Klassen ziehen, fallen die Ergebnisse jedes Mal recht unterschiedlich aus. Daher ist es unbedingt erforderlich, die Robustheit des Modells bei kleinen Stichproben zu verbessern.
Kürzlich haben Tencent Youtu Lab und die Universität Wuhan ein Zielerkennungsmodell VFA mit wenigen Stichproben vorgeschlagen, das auf der Aggregation von Variationsmerkmalen basiert. Die Gesamtstruktur von VFA basiert auf einer verbesserten Version des Meta-Learning-Zielerkennungs-Frameworks Meta R-CNN++, und es werden zwei Methoden zur Merkmalsaggregation vorgeschlagen: Class-Agnostic Aggregation CAA (Class-Agnostic Aggregation) und Variationsmerkmalsaggregation VFA (Variationsmerkmalsaggregation).
Feature-Aggregation ist ein Schlüsseldesign in FSOD, das die Interaktion zwischen Abfrage- und Support-Beispielen definiert. Frühere Methoden wie Meta R-CNN verwenden normalerweise die klassenspezifische Aggregation (CSA), d. h. Features ähnlicher Abfrage- und Supportbeispiele für die Feature-Aggregation. Im Gegensatz dazu ermöglicht die in diesem Artikel vorgeschlagene CAA die Merkmalsaggregation zwischen Stichproben verschiedener Klassen. Da CAA das Modell dazu ermutigt, klassenunabhängige Darstellungen zu lernen, verringert es die Ausrichtung des Modells auf Basisklassen. Darüber hinaus können Interaktionen zwischen verschiedenen Klassen die Beziehungen zwischen Klassen besser modellieren und so die Klassenverwirrung verringern.Basierend auf CAA schlägt dieses Papier VFA vor, das Variationsencoder (VAEs) verwendet, um Support-Beispiele in Klassenverteilungen zu codieren, und neue Support-Funktionen aus der erlernten Verteilung für die Feature-Fusion zu testen. In einer verwandten Arbeit [1] heißt es, dass die Varianz innerhalb der Klasse (z. B. Variation im Aussehen) zwischen den Klassen ähnlich ist und durch gemeinsame Verteilungen modelliert werden kann. Daher können wir die Verteilung der Basisklassen verwenden, um die Verteilung neuer Klassen abzuschätzen und so die Robustheit der Merkmalsaggregation bei wenigen Stichproben zu verbessern.
VFA schneidet bei mehreren FSOD-Datensätzen besser ab als die derzeit besten Modelle. Verwandte Forschung wurde von AAAI 2023 als mündlich anerkannt.

Papieradresse: https://arxiv.org/abs/2301.13411VFA-Modelldetails
Stärkere Basismethode: Meta R-CNN++
Aktueller FSOD Die Arbeit kann hauptsächlich in zwei Kategorien unterteilt werden: Methoden, die auf Meta-Lernen basieren, und Methoden, die auf Feinabstimmung basieren. Einige frühe Arbeiten zeigten, dass Meta-Learning für FSOD effektiv ist, aber auf Feinabstimmung basierende Methoden haben in letzter Zeit zunehmende Aufmerksamkeit erhalten.In diesem Artikel wird zunächst eine auf Meta-Learning basierende Basismethode Meta R-CNN++ etabliert, die die Lücke zwischen den beiden Methoden verringert und bei einigen Indikatoren sogar die Methode übertrifft, die auf der Feinabstimmung basiert.
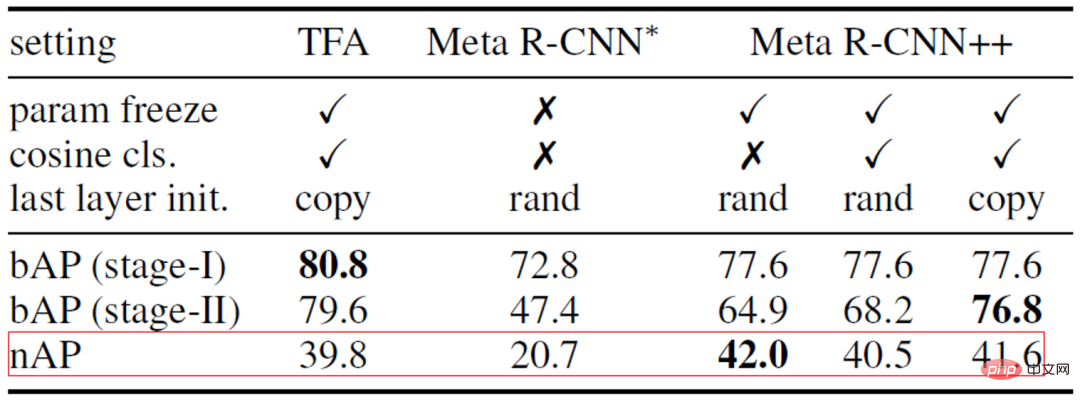
Wir haben zunächst einige Lücken in der Implementierung der beiden Methoden analysiert und dabei die Meta-Lernmethode Meta R-CNN [2] und die auf Feinabstimmung basierende Methode TFA [3] als Beispiele genommen, obwohl beide Methoden a folgen Beim zweistufigen Trainingsparadigma optimiert TFA das Modell mithilfe zusätzlicher Techniken während der Feinabstimmungsphase:Angesichts des Erfolgs von TFA haben wir Meta R-CNN++ entwickelt. Wie in Tabelle 1 unten gezeigt, können auch Meta-Lernmethoden gute Ergebnisse erzielen, sofern wir die Feinabstimmungsphase sorgfältig durchführen. Daher wählt dieser Artikel Meta R-CNN++ als Basismethode. Tabelle 1: Vergleich und Analyse von Meta R-CNN und TFA Kategorieunabhängige Feature-Aggregation. CAA Bild 1: Schematische Darstellung der kategorieunabhängigen Feature-Aggregation CAA
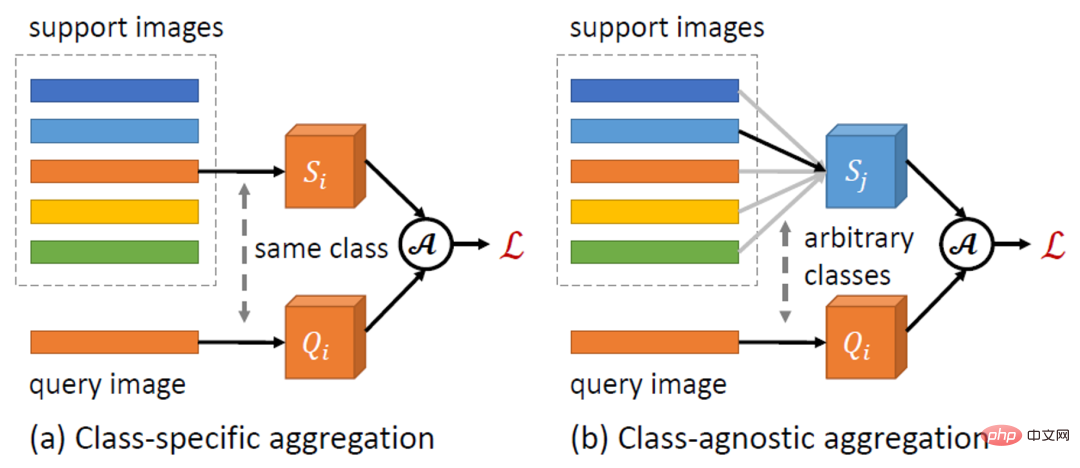
Dieser Artikel schlägt eine einfache und effektive kategorieunabhängige Feature-Aggregation-Methode CAA vor. Wie in Abbildung 1 oben dargestellt, ermöglicht CAA die Aggregation von Merkmalen zwischen verschiedenen Klassen und ermutigt so das Modell, klassenunabhängige Darstellungen zu lernen, wodurch die Verzerrung zwischen den Klassen und die Verwirrung zwischen den Klassen verringert werden. Konkret wählen wir für jedes RoI-Feature der Klasse und eine Reihe von Support-Features  ,
, 
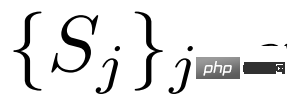 zufällig das Support-Feature einer Klasse
zufällig das Support-Feature einer Klasse  aus, das mit dem Abfragefeature aggregiert werden soll:
aus, das mit dem Abfragefeature aggregiert werden soll: 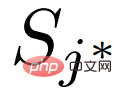
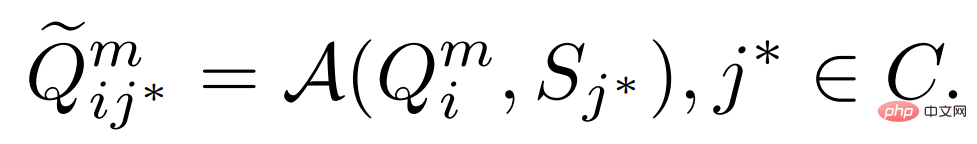 Dann geben wir die aggregierten Merkmale
Dann geben wir die aggregierten Merkmale
an das Erkennungs-Subnetzwerk 
weiter, um einen Klassifizierungswert  auszugeben
auszugeben
.
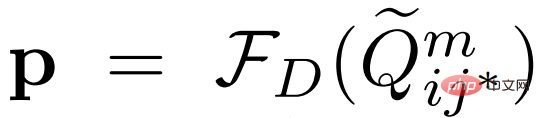
Frühere Arbeiten codierten Support-Beispiele normalerweise in einen einzelnen Feature-Vektor, um das Zentrum der Kategorie darzustellen. Wenn die Stichproben jedoch klein und die Varianz groß sind, ist es für uns schwierig, genaue Schätzungen des Klassenzentrums vorzunehmen. In diesem Artikel konvertieren wir zunächst die Support-Funktionen in Verteilungen über Klassen. Da die geschätzte Klassenverteilung nicht auf bestimmte Stichproben ausgerichtet ist, sind aus der Verteilung entnommene Merkmale relativ robust gegenüber der Varianz der Stichproben. Der Rahmen von VFA ist in Abbildung 2 oben dargestellt. a) Variationelles Feature-Lernen. VFA verwendet Variations-Autoencoder-VAEs [4], um die Verteilung von Kategorien zu lernen. Wie in Abbildung 2 dargestellt, verwenden wir für ein Support-Feature S zunächst den Encoder 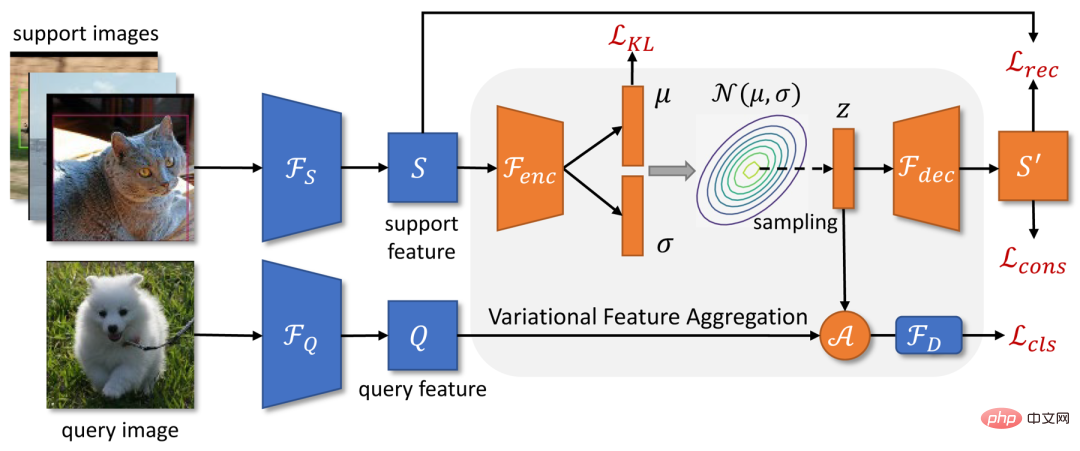
 , um die Parameter der Verteilung
, um die Parameter der Verteilung  und
und  zu schätzen, und nehmen dann Stichproben aus der Verteilung
zu schätzen, und nehmen dann Stichproben aus der Verteilung 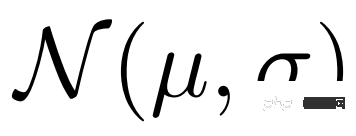 durch Variationsinferenz
durch Variationsinferenz  , und schließlich wird die rekonstruierte Support-Funktion
, und schließlich wird die rekonstruierte Support-Funktion  über den Decoder
über den Decoder  abgerufen. Bei der Optimierung von VAE wird in diesem Artikel neben dem üblichen KL-Verlust
abgerufen. Bei der Optimierung von VAE wird in diesem Artikel neben dem üblichen KL-Verlust und dem Rekonstruktionsverlust
und dem Rekonstruktionsverlust auch der Konsistenzverlust verwendet, damit die erlernte Verteilung die Kategorieinformationen beibehält:
auch der Konsistenzverlust verwendet, damit die erlernte Verteilung die Kategorieinformationen beibehält:
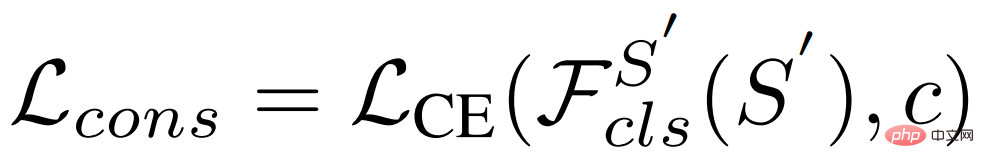
b) Variationelle Feature-Fusion. Da die Support-Funktion in eine Verteilung von Kategorien umgewandelt wird, können wir Features aus der Verteilung auswählen und sie mit der Abfragefunktion aggregieren. Insbesondere verwendet VFA auch kategorieunabhängige Aggregations-CAA, aggregiert jedoch Abfragefunktionen  und Variationsfunktionen
und Variationsfunktionen  zusammen. Bei einer Abfragefunktion der Klasse
zusammen. Bei einer Abfragefunktion der Klasse  und einer Supportfunktion der Klasse
und einer Supportfunktion der Klasse 
 schätzen wir zunächst deren Verteilung
schätzen wir zunächst deren Verteilung  und führen eine Stichprobenvariation durch Funktionen
und führen eine Stichprobenvariation durch Funktionen
und verschmelzen sie dann mit der folgenden Formel: 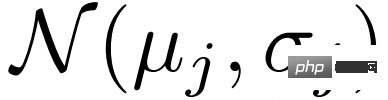 # 🎜🎜#
# 🎜🎜#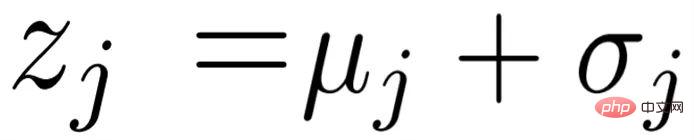 #🎜 🎜#
#🎜 🎜#
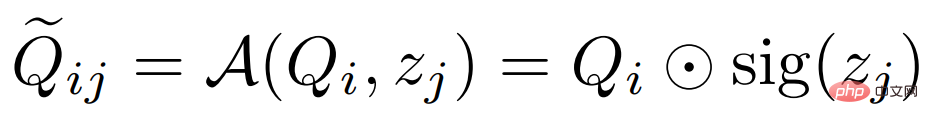 die Kanalmultiplikation darstellt und sig die Abkürzung für Sigmoidoperation ist. In der Trainingsphase wählen wir zufällig eine Support-Funktion
die Kanalmultiplikation darstellt und sig die Abkürzung für Sigmoidoperation ist. In der Trainingsphase wählen wir zufällig eine Support-Funktion
wie  # 🎜🎜# Unterstützungsfunktionen werden gemittelt
# 🎜🎜# Unterstützungsfunktionen werden gemittelt 
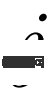 und die Verteilung wird geschätzt
und die Verteilung wird geschätzt
, wobei Typischerweise enthält das Erkennungs-Subnetzwerk  #🎜 🎜 #.
#🎜 🎜 #. 
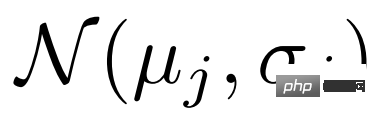 Klassifizierung – Entkopplung von Regressionsaufgaben
Klassifizierung – Entkopplung von Regressionsaufgaben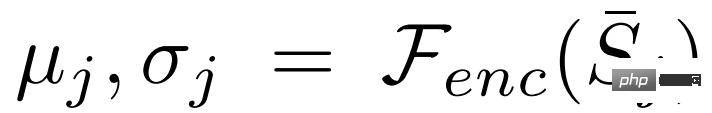
 einen gemeinsamen Feature-Extraktor
einen gemeinsamen Feature-Extraktor 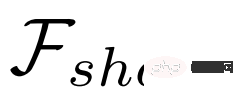 und Zwei unabhängige Netzwerke: Klassifizierungs-Subnetzwerk
und Zwei unabhängige Netzwerke: Klassifizierungs-Subnetzwerk  und Regressions-Subnetzwerk
und Regressions-Subnetzwerk  . In früheren Arbeiten wurden die aggregierten Merkmale zur Objektklassifizierung und Bounding-Box-Regression in das Erkennungssubnetzwerk eingegeben. Für Klassifizierungsaufgaben sind jedoch übersetzungsinvariante Merkmale erforderlich, während für die Regression übersetzungskovariante Merkmale erforderlich sind. Da das Support-Feature das Zentrum der Kategorie darstellt und übersetzungsinvariant ist, beeinträchtigen die aggregierten Features die Regressionsaufgabe.
. In früheren Arbeiten wurden die aggregierten Merkmale zur Objektklassifizierung und Bounding-Box-Regression in das Erkennungssubnetzwerk eingegeben. Für Klassifizierungsaufgaben sind jedoch übersetzungsinvariante Merkmale erforderlich, während für die Regression übersetzungskovariante Merkmale erforderlich sind. Da das Support-Feature das Zentrum der Kategorie darstellt und übersetzungsinvariant ist, beeinträchtigen die aggregierten Features die Regressionsaufgabe.
Dieser Artikel schlägt eine einfache Entkopplung von Klassifizierungs- und Regressionsaufgaben vor. Lassen Sie  und
und  die ursprünglichen und aggregierten Abfragefunktionen darstellen. Die vorherige Methode übernimmt # für beide Aufgaben.
die ursprünglichen und aggregierten Abfragefunktionen darstellen. Die vorherige Methode übernimmt # für beide Aufgaben.  , wobei der Klassifizierungswert
, wobei der Klassifizierungswert  und der vorhergesagte Begrenzungsrahmen
und der vorhergesagte Begrenzungsrahmen  wie folgt definiert sind:
wie folgt definiert sind:
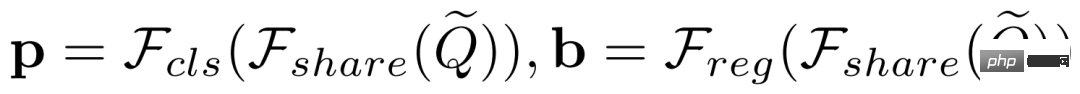
Um diese Aufgaben zu entkoppeln, übernehmen wir separate Feature-Extraktoren und verwenden die ursprünglichen Support-Features#🎜🎜 ##🎜 🎜#Bounding-Box-Regression durchführen: #Experimentelle Auswertung Der von uns verwendete Datensatz:
Der von uns verwendete Datensatz:
PASCAL VOC, MS COCO.
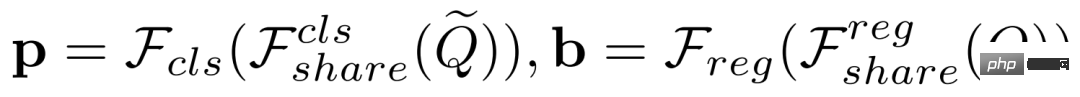
Novel-Klasse durchschnittliche Präzision nAP, Basisklasse durchschnittliche Präzision bAP
Ablationsexperiment a) Die Rolle verschiedener Module# 🎜 🎜#. Wie in Tabelle 3 unten gezeigt, können verschiedene VFA-Module zusammenarbeiten, um die Leistung des Modells zu verbessern. b) Visuelle Analyse verschiedener Feature-Aggregation-Methoden #🎜 🎜#. Wie in Abbildung 3 unten dargestellt, kann CAA die Verwirrung zwischen Basisklassen und neuartigen Klassen verringern und die Unterscheidung zwischen auf CAA basierenden Klassen weiter verbessern. Abbildung 5 Visualisierungsergebnisse#🎜 🎜# Fazit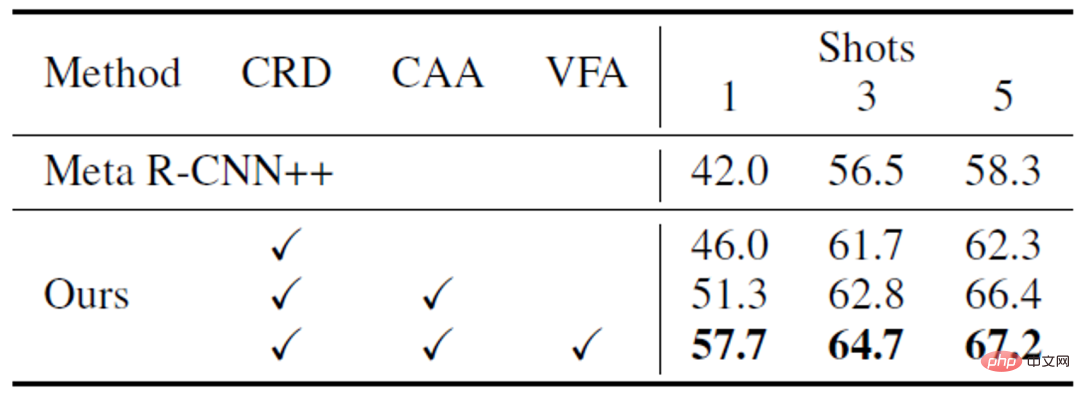
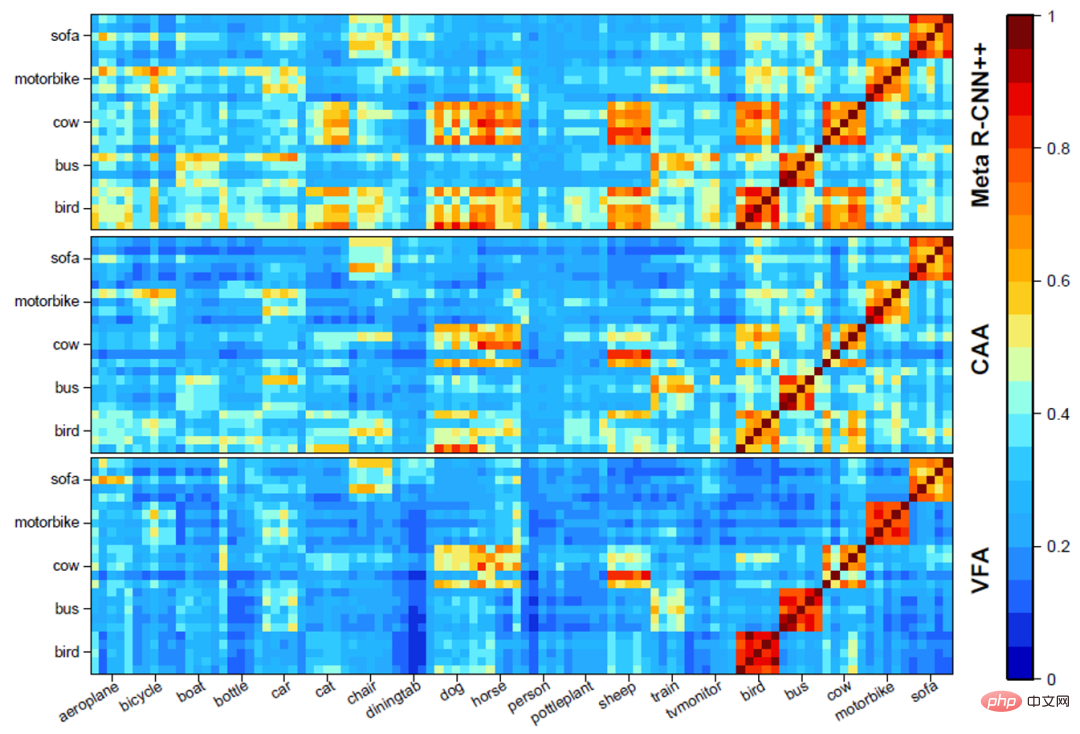
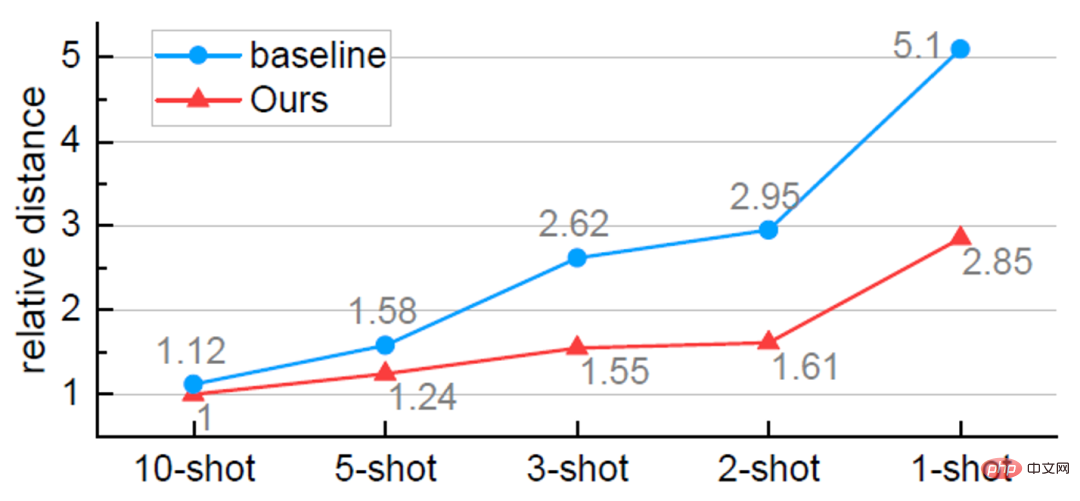 Dieses Papier kehrt zur Feature-Aggregation-Methode in FSOD basierend auf Meta-Learning zurück und schlägt Kategorien vor. Unabhängige Features Aggregate CAA und Variationsfeature Aggregation VFA. CAA kann Klassenverzerrungen und Verwirrung zwischen Basisklassen und neuartigen Klassen reduzieren; VFA wandelt Stichproben in Klassenverteilungen um, um eine robustere Merkmalsaggregation zu erreichen. Experimente mit den PASCAL VOC- und MS COCO-Datensätzen zeigen die Wirksamkeit der in diesem Artikel vorgeschlagenen Methode.
Dieses Papier kehrt zur Feature-Aggregation-Methode in FSOD basierend auf Meta-Learning zurück und schlägt Kategorien vor. Unabhängige Features Aggregate CAA und Variationsfeature Aggregation VFA. CAA kann Klassenverzerrungen und Verwirrung zwischen Basisklassen und neuartigen Klassen reduzieren; VFA wandelt Stichproben in Klassenverteilungen um, um eine robustere Merkmalsaggregation zu erreichen. Experimente mit den PASCAL VOC- und MS COCO-Datensätzen zeigen die Wirksamkeit der in diesem Artikel vorgeschlagenen Methode.
Das obige ist der detaillierte Inhalt vonRegressions-Meta-Lernen, Zielerkennung mit wenigen Stichproben basierend auf der Aggregation von Variationsmerkmalen, um neue SOTA zu erreichen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Technologietrends, die Sie im Jahr 2023 im Auge behalten sollten
- Wie künstliche Intelligenz Rechenzentrumsteams neue Alltagsaufgaben beschert
- Können künstliche Intelligenz oder Automatisierung das Problem der geringen Energieeffizienz in Gebäuden lösen?
- OpenAI-Mitbegründer im Interview mit Huang Renxun: Die Argumentationsfähigkeiten von GPT-4 haben noch nicht die Erwartungen erfüllt
- Dank der OpenAI-Technologie übertrifft Bing von Microsoft Google im Suchverkehr

