Heim >Technologie-Peripheriegeräte >KI >Flugbahnvorhersage und -planung für autonomes Fahren unter Zwangsverschmelzung
Flugbahnvorhersage und -planung für autonomes Fahren unter Zwangsverschmelzung
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2023-04-12 17:19:031317Durchsuche
Generell ist das Zusammenführen sowohl für autonomes als auch für bemanntes Fahren eine herausfordernde Aufgabe, insbesondere in Szenarien mit dichtem Verkehrsfluss, da zusammenführende Fahrzeuge normalerweise mit anderen Fahrzeugen interagieren müssen, um Platz für eine sichere Einbindung zu schaffen. In diesem Artikel wird das Steuerungsproblem autonomer Fahrzeuge in erzwungenen Zusammenführungsszenarien untersucht. Wir schlagen einen neuen spielbasierten Controller namens Leader-Follower Game Controller (LFGC) vor.
Dabei wird ein teilweise beträchtliches Leader-Follower-Spielmodell verwendet, um die Interaktion zwischen selbstfahrenden Fahrzeugen und anderen Fahrzeugen mit a priori unsicherem Fahrverhalten zu modellieren. LFGC schätzt online die Absichten anderer Fahrzeuge auf der Grundlage der beobachteten Flugbahnen, sagt deren zukünftige Flugbahnen voraus und verwendet modellprädiktive Steuerung (MPC), um die Flugbahn des eigenen Fahrzeugs zu planen, um die Sicherheitswahrscheinlichkeit sicherzustellen und gleichzeitig das Zusammenführungsziel zu erreichen. Um die Leistung von LFGC zu überprüfen, haben wir es mithilfe von Simulationen und NGSIM-Daten getestet, wobei LFGC eine Erfolgsquote bei der Integration von bis zu 97,5 % zeigte.
01 Einleitung
Die Realisierung hochautonomer Fahrzeuge steht noch vor vielen Herausforderungen [4 ] ist die Durchführung einer Zwangszusammenführung auf der Autobahn ein herausforderndes Szenario sowohl für bemanntes als auch für autonomes Fahren. Unter erzwungenem Einfädeln versteht man in der Regel das Szenario, in dem die aktuelle Fahrspur endet und ein erzwungenes Einfädeln erforderlich ist, beispielsweise das Einfädeln an einer Autobahnauffahrt. Bei starkem Verkehr interagieren und/oder kooperieren zusammenfahrende Fahrzeuge mit Fahrzeugen, die auf der Zielspur fahren.
Zu diesem Zeitpunkt kann das Fahrzeug auf der Zielspur das einfädelnde Fahrzeug ignorieren (d. h. weiterfahren) und das einfädelnde Fahrzeug kann nur dahinter einfädeln , Fahrzeuge auf der Zielspur können sich dafür entscheiden, dem Einfädler nachzugeben (d. h. das einfädelnde Fahrzeug vor sich einfädeln zu lassen). Um erfolgreich in dichte Verkehrsströme einzupassen, müssen autonome Fahrzeugsteuerungen die Absicht der Fahrzeuge auf der Zielspur, weiterzufahren oder auszuweichen, vernünftig vorhersagen, um angemessen reagieren zu können.
Gleichzeitig hängt die Absicht des anderen Autos nicht nur von den Verkehrsbedingungen (wie der relativen Position und Geschwindigkeit zwischen den beiden Autos) ab, sondern auch von den allgemeinen Eigenschaften des Fahrers, seiner Persönlichkeit, seiner Stimmung usw. Beispielsweise könnte ein aggressiver Fahrer dazu neigen, weiterzufahren, während ein vorsichtiger, konservativer Fahrer dazu neigen könnte, nachzugeben. Dies stellt die Planung und Steuerung autonomer Fahrzeuge vor erhebliche Herausforderungen. #? 🎜#
Derzeit verwenden viele Wissenschaftler das Partially Observable Markov Decision Process (POMDP)-Framework, um mit interaktiven Unsicherheiten umzugehen (z. B. aufgrund der unterschiedlichen Zusammenarbeit anderer Autos). Allerdings erfordert diese Methode einen hohen Rechenaufwand [11] und lässt sich nur schwer für die Interaktion mehrerer Fahrzeuge verwenden. 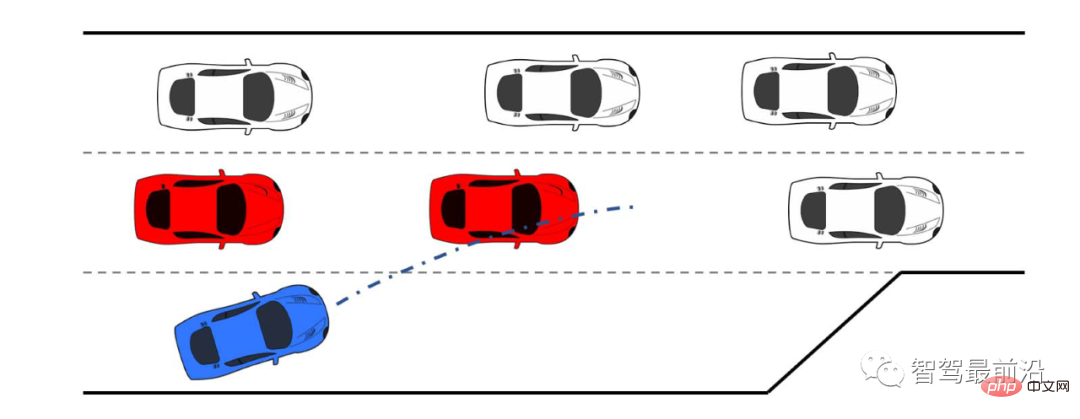
Die Reinforcement-Learning-Methode (RL) ist eine weitere beliebte Methode zum Festlegen von Kontrollstrategien für Spurwechsel- oder Einfädelungsszenarien [12][13]. RL-basierte Methoden sind in der Lage, komplexe Interaktionsszenarien mit mehreren Fahrzeugen im Straßenverkehr zu bewältigen, RL mangelt es jedoch an Interpretierbarkeit und klaren Sicherheitsgarantien. Um eine besser interpretierbare Steuerung zu erreichen, haben einige Forscher vorgeschlagen, dem Steuerungsalgorithmus explizit ein Vorhersagemodell der Fahrzeuginteraktion hinzuzufügen. Beispielsweise nutzt [22] das „Social Generative Adversarial Network (GAN)“, um die zukünftige Flugbahn anderer Autos als Reaktion auf das Verhalten des eigenen Autos vorherzusagen. SocialGAN berücksichtigt jedoch keine Änderungen im Stil und in der Absicht des Fahrers und erfordert umfangreiche Verkehrsdaten [23] für das Training. Einige Studien verwenden spieltheoretische Methoden, um Spurwechsel- oder -zusammenführungsszenarien zu modellieren [9], [25], Fahrzeuginteraktionen unter [26], [27], [28], [29] können unterschiedliche Fahrstile und/oder -absichten berücksichtigen, beispielsweise durch Spielmodellierung und Online-Schätzung des kognitiven Niveaus des Fahrers [26] oder [30], [31]. ].
In diesem Artikel wird ein neuer fortschrittlicher Steuerungsalgorithmus namens Leader-Follower Game Controller (LFGC) für die erzwungene Zusammenführungsplanung und -steuerung autonomer Fahrzeuge vorgeschlagen. Bei LFGC wird die explizite Spieltheorie verwendet, um die Interaktionsabsicht des Fahrers (Weiterfahren oder Nachgeben) und das daraus resultierende Fahrzeugverhalten zu modellieren.
Da das Modell über mehrere parallele Leader-Follower-Paare verfügt, wird es als Leader-Follower-Spiel bezeichnet [32]. Unter Berücksichtigung der Unsicherheit der Interaktion wird die a priori unsichere Leader-Follower-Beziehung zwischen zwei Fahrzeugen als latente Variable modelliert. LFGC schätzt die Leader-Follower-Beziehung online auf Basis der beobachteten Trajektorien und nutzt eine auf Model Predictive Control (MPC) basierende Strategie, um optimale Entscheidungen für das autonome Fahrzeug zu treffen.
Daher ist das vorgeschlagene LFGC so angepasst, dass es die vorhergesagte Leader-Follower-Beziehung bewertet, um probabilistische Sicherheit bei gleichzeitiger Verschmelzung zu gewährleisten.
Im Vergleich zu bestehenden Methoden sind die Beiträge und Innovationen von LFGC wie folgt:
1) Verwenden Sie das LFGC-Spielmodell, um Fahrzeugtrajektorien unter Berücksichtigung von Interaktionen mit anderen Fahrzeugen und Kooperationsabsichten vorherzusagen und interpretierbare Ergebnisse zu generieren Nach dem Zugriff auf das MPC-Steuerungsschema.
2) LFGC behandelt die interaktive Unsicherheit, die durch die unterschiedlichen Kooperationsabsichten anderer Fahrzeuge verursacht wird, indem es die Unsicherheit als latente Variable modelliert und eine Bayes'sche Inferenz-Online-Schätzung basierend auf der historischen Beobachtungstrajektoriensammlung durchführt.
3) LFGC legt Einschränkungen für Fahrzeugsicherheitsanforderungen fest (z. B. Kollisionsvermeidung) und führt eine Optimierung durch, während klare probabilistische Sicherheitsmerkmale erfüllt werden (d. h. innerhalb der vom Benutzer festgelegten Sicherheitswahrscheinlichkeitsgrenzen).
4) LFGC wurde unter einer kontinuierlichen Zustandsraumeinstellung entwickelt, was die Rechenkosten des diskreten Raums reduziert und komplexere Interaktionsszenarien mit mehreren Fahrzeugen bewältigen kann.
5) Die Machbarkeit von LFGC wird durch umfassende, auf Simulationen basierende Fallstudien verifiziert, einschließlich Fällen, in denen andere Fahrzeuge durch verschiedene Arten von Fahrermodellen gesteuert werden, sowie tatsächlicher Fälle im Fall des NGSIM US Highway 101-Datensatzes [34]. . Und in realen Fallsimulationen zeigt es eine Erfolgsquote von bis zu 97,5 %.
02 Beschreibung der Modell- und Steuerungsstrategie
In diesem Abschnitt wird eine MPC-basierte Strategie zur Planung der Eigenfahrzeugtrajektorie basierend auf dem Modell erstellt, das die Fahrzeug- und Verkehrsdynamik darstellt.
Fahrzeugdynamikmodell
Bei unserer Verwendung des kinematischen Fahrradmodells [35] lautet die kontinuierliche Zeitgleichung des Fahrradmodells wie folgt:
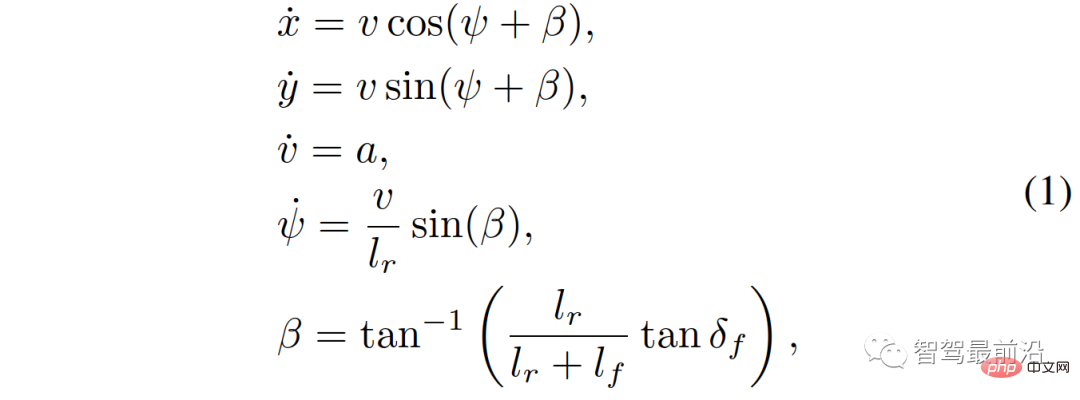
nur Vorderrad vorausgesetzt Lenkung  , es gibt keine Hinterradlenkung (d. h.
, es gibt keine Hinterradlenkung (d. h.  ); v ist die Geschwindigkeit des Fahrzeugs; ψ und β sind der Gierwinkel und Schräglaufwinkel von das Fahrzeug;
); v ist die Geschwindigkeit des Fahrzeugs; ψ und β sind der Gierwinkel und Schräglaufwinkel von das Fahrzeug;  und
und 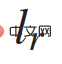 stellt den Abstand des Fahrzeugs vom Schwerpunkt zum Vorderrad und zur Hinterachse dar; a ist die Beschleunigung entlang der Geschwindigkeits-v-Richtung; Steuereingaben sind Beschleunigung und Vorderradlenkung,
stellt den Abstand des Fahrzeugs vom Schwerpunkt zum Vorderrad und zur Hinterachse dar; a ist die Beschleunigung entlang der Geschwindigkeits-v-Richtung; Steuereingaben sind Beschleunigung und Vorderradlenkung, 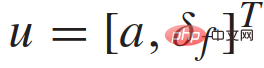 .
.
Dynamische Verkehrseinstellung
Die Szene umfasst 1 eigenes Fahrzeug und n andere Fahrzeuge. Der Verkehrszustand und seine Dynamik werden durch die Aggregation der Zustände und Dynamiken aller n+1 Fahrzeuge charakterisiert. Konkret wird zur Beschreibung der Verkehrsdynamik das folgende diskrete Zeitmodell verwendet:
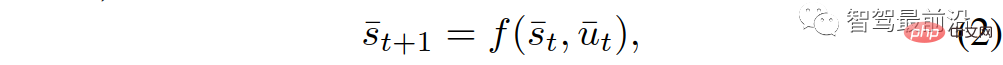
wo, 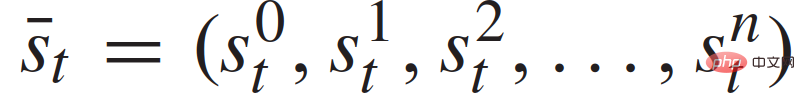
stellt den Verkehrsstatus von n + 1 Fahrzeugen zu diskreten Zeitpunkten dar und 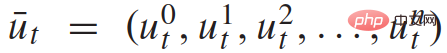 stellt den Satz von Steuereingaben aller n + 1 Fahrzeuge zum Zeitpunkt t dar. Der Zustand jedes Fahrzeugs
stellt den Satz von Steuereingaben aller n + 1 Fahrzeuge zum Zeitpunkt t dar. Der Zustand jedes Fahrzeugs 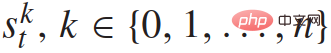 umfasst seine xy-Koordinaten, Geschwindigkeit und Gierwinkel; die Steuereingabe
umfasst seine xy-Koordinaten, Geschwindigkeit und Gierwinkel; die Steuereingabe 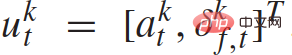
Belohnungsfunktion
Die Belohnungsfunktion
ist eine mathematische Darstellung der Fahrweise des Fahrers Ziel: Der Verkehrszustand setzt sich aus den Zuständen der beiden Fahrzeuge zusammen und die vom eigenen Fahrzeug erhaltene Belohnung hängt von den Zuständen und Steuereingaben der beiden interagierenden Fahrzeuge ab. Wir betrachten 
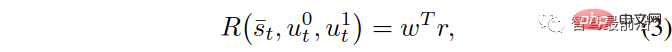 Unter ihnen
Unter ihnen 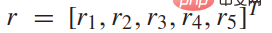 , ist ein Gewicht Vektor. Die Bonuselemente
, ist ein Gewicht Vektor. Die Bonuselemente  repräsentieren die folgenden allgemeinen Überlegungen beim Fahren: 1) Sicherheit
repräsentieren die folgenden allgemeinen Überlegungen beim Fahren: 1) Sicherheit  , d Spur; 3) Komfort
, d Spur; 3) Komfort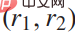 , das heißt, einen angemessenen Abstand zu anderen Autos einhalten. Eine detailliertere Definition von
, das heißt, einen angemessenen Abstand zu anderen Autos einhalten. Eine detailliertere Definition von 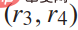 finden Sie in [33].
finden Sie in [33]. 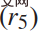

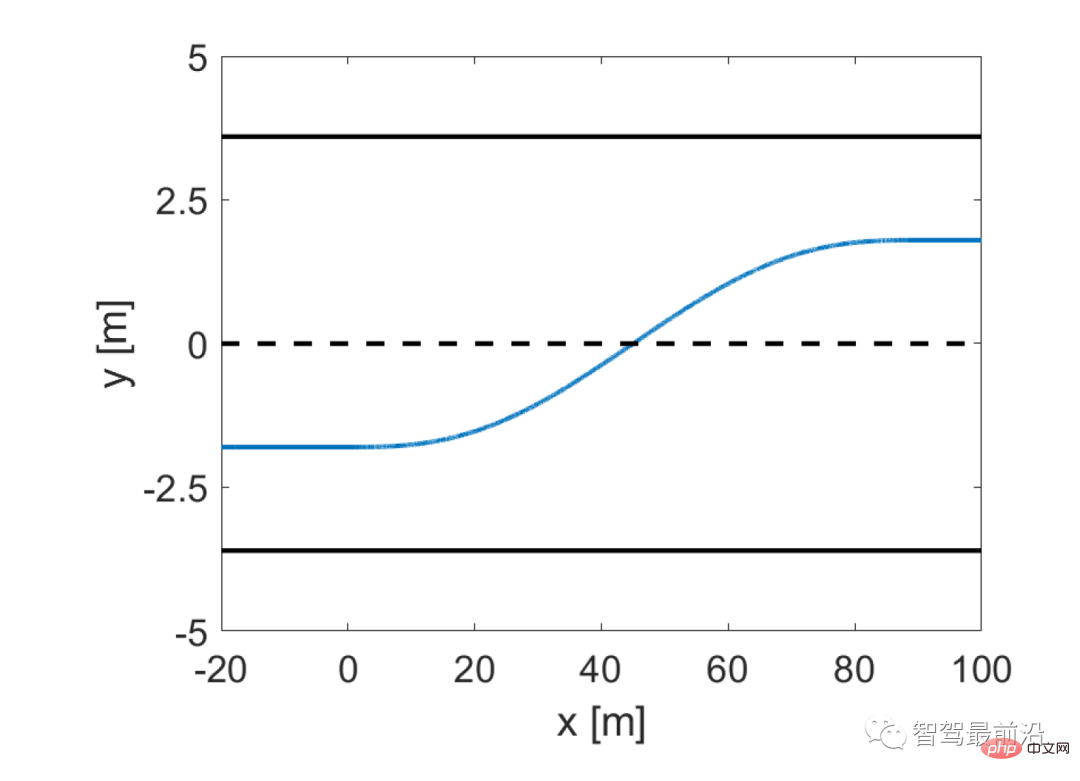 Abbildung 2 Spurwechselkurve mit fünf Freiheitsgraden
Abbildung 2 Spurwechselkurve mit fünf Freiheitsgraden
Trajektorien als Fahrzeugaktionen auswählen
Wir betrachten Muster von Fahrzeugbewegungstrajektorien auf 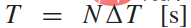 als Aktionsraum jedes Fahrzeugs. Konkret handelt es sich bei jeder Trajektorie um den zeitlichen Verlauf des Fahrzeugzustands
als Aktionsraum jedes Fahrzeugs. Konkret handelt es sich bei jeder Trajektorie um den zeitlichen Verlauf des Fahrzeugzustands 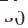
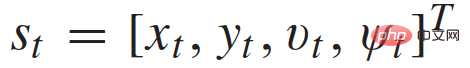 . Gemäß dem Fahrzeugdynamikmodell (1) kann der Zeitverlauf der Steuereingabe
. Gemäß dem Fahrzeugdynamikmodell (1) kann der Zeitverlauf der Steuereingabe
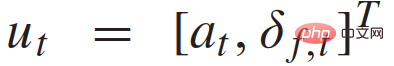 entsprechend jeder Trajektorie berechnet werden.
entsprechend jeder Trajektorie berechnet werden.
Bei interaktiven Fahrzeugen, die auf der Zielspur fahren, berücksichtigen wir nur deren Längsbewegung.
Unter der Annahme  und
und  vereinfacht sich das kinematische Modell (1) dieser Fahrzeuge zu:
vereinfacht sich das kinematische Modell (1) dieser Fahrzeuge zu: 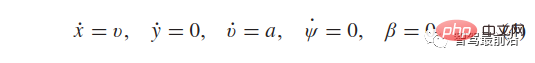
Zu diesem Zeitpunkt hängt die Flugbahn ausgehend von den gegebenen Anfangsbedingungen nur von der Beschleunigung a von [0, T] ab. Zu jedem Abtastzeitpunkt werden 81 Beschleunigungskurven berücksichtigt, d.
Diese 81 Trajektorien entsprechen den Geschwindigkeitsbeschränkungen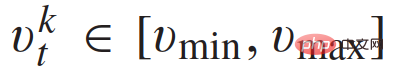 .
.
Bezeichnen Sie jede Trajektorie als 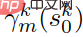 , m = 1,2,...81, und der Satz von Trajektorien wird als
, m = 1,2,...81, und der Satz von Trajektorien wird als 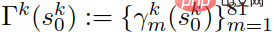
Die Trajektorienstrategie des zusammengeführten Fahrzeugs umfasst Spurhaltung und Spurwechsel: Die Erzeugung der Spurhaltetrajektorie ähnelt (4) und die Spurwechseltrajektorie wird durch ein Polynom fünfter Ordnung dargestellt [37]. Das heißt, die Lösung für die Spurwechsel-Trajektorienanforderung kann als folgendes Randwertproblem modelliert werden:
Finden Sie die Koeffizienten  und
und  , damit das Polynom 5. Ordnung
, damit das Polynom 5. Ordnung
die entsprechenden Anfangswertbedingungen und Endwertbedingungen erfüllt. Die Variable ζ in (5) stellt die kontinuierliche Zeit dar und ζ=0 für die aktuelle Probe.
Es wird außerdem davon ausgegangen, dass 1) das Fahrzeug zu jedem Beispielzeitpunkt innerhalb des Planungsbereichs mit dem Spurwechsel beginnen kann, 2) die für einen vollständigen Spurwechsel erforderliche Zeit konstant ist [37]. Dadurch kann das Fahrzeug das Spurwechselverhalten jederzeit während des Spurwechselvorgangs beenden, was den „Umdenken“ des Fahrers darstellt, wenn der zuvor geplante Spurwechsel nicht mehr durchführbar/sicher wird. Die Trajektorie nach Abbruch des Spurwechsels wird auf ähnliche Weise wie die Spurwechseltrajektorie generiert.
Abschließend werden die Trajektorien des Spurhaltens, des Spurwechsels und des Abbruchs des Spurwechsels gespleißt und zu 162 Trajektorien zusammengefasst, die als realisierbarer Bereich der Strategie verwendet werden.
Die Trajektorienmerkmale werden wie folgt extrahiert: 1) ob/wann ein Spurwechsel begonnen werden soll, 2) ob/wann ein unangemessener Spurwechsel beendet werden soll.
Abbildung 3 zeigt den Trajektorien-Sampling-Satz, wenn das Fahrzeug nicht mit dem Spurwechsel beginnt und wenn das Fahrzeug gerade dabei ist, die Spur zu wechseln. Bezeichnen Sie jede Trajektorie als,m = 1,2,...,162; die Trajektorienmenge ist,.
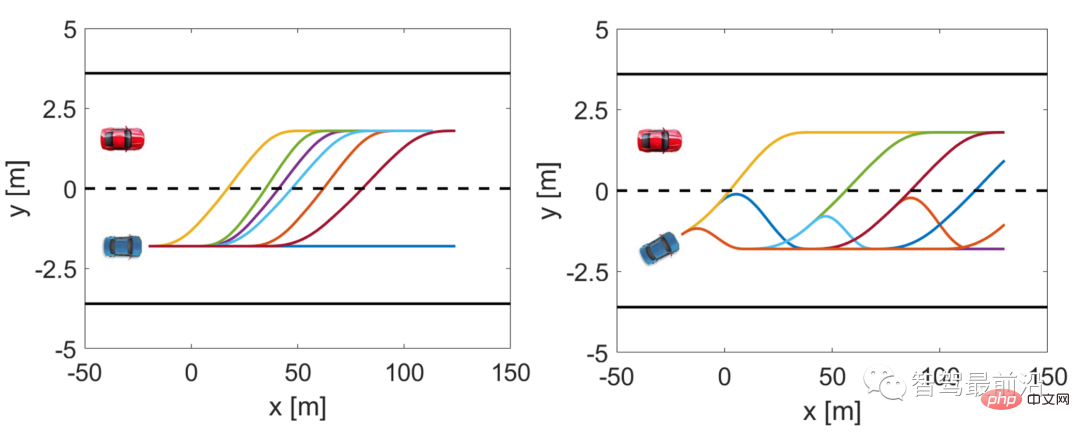
Abbildung 3 Trajektorienbeispiel des fusionierten Fahrzeugs
Zusammenfassend wird die mögliche Trajektorie als Entscheidungsausgabe definiert. Gleichzeitig kann auf Basis des Fahrdynamikmodells (1) der zeitliche Verlauf der diesen Trajektorien entsprechenden Steuereingaben berechnet werden. Die geplante Trajektorie kann tatsächlich an die zugrunde liegende Fahrzeugbewegungssteuerung übertragen werden.
Strategie zur modellprädiktiven Steuerung
Betrachten Sie die auf MPC basierende autonome autonome Fahrzeug-Trajektorienplanungsstrategie unter Berücksichtigung der Anwesenheit signalinteragierender Fahrzeuge: Zu jedem Abtastzeitpunkt t berechnet das autonome Fahrzeug ein Optimum Flugbahn, 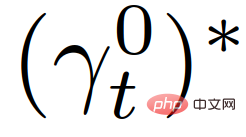 , basierend auf der Maximierung ihrer kumulativen Belohnung innerhalb des Planungsbereichs:
, basierend auf der Maximierung ihrer kumulativen Belohnung innerhalb des Planungsbereichs:
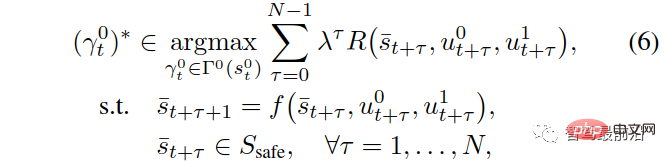
wobei 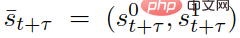 den vorhergesagten Verkehrsstatus zum diskreten Zeitpunkt t+τ darstellt, während
den vorhergesagten Verkehrsstatus zum diskreten Zeitpunkt t+τ darstellt, während 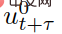 und
und 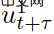
stellen die vorhergesagten Steuereingaben des eigenen Fahrzeugs bzw. des interaktiven Fahrzeugs bei t+τ dar. Der Parameter λ∈(0,1) ist der Gewinn- und Verlustkoeffizient zukünftiger Belohnungen, d. h. den aktuellen Belohnungen wird Priorität eingeräumt. In (6), 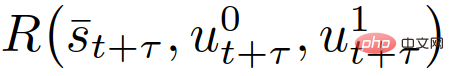
stellt die Belohnung des eigenen Fahrzeugs bei t+τ dar, wie in Abschnitt II-C beschrieben,  stellt eine Reihe von Sicherheitswerten für Verkehrszustände dar, die zur Umsetzung strenger Sicherheitsspezifikationen (z. B. Antikollision) verwendet werden , Straßenbegrenzungsbeschränkungen usw. ). Nachdem die optimale Trajektorie
stellt eine Reihe von Sicherheitswerten für Verkehrszustände dar, die zur Umsetzung strenger Sicherheitsspezifikationen (z. B. Antikollision) verwendet werden , Straßenbegrenzungsbeschränkungen usw. ). Nachdem die optimale Trajektorie 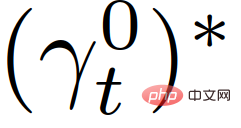 erhalten wurde, verwendet das Eigenfahrzeug die der Trajektorie entsprechende Steuereingabe
erhalten wurde, verwendet das Eigenfahrzeug die der Trajektorie entsprechende Steuereingabe 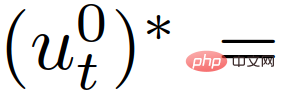
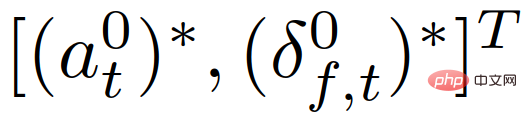 , aktualisiert seinen Zustand innerhalb einer Abtastperiode und wiederholt dann die oben genannten Schritte zum nächsten Abtastzeitpunkt t+1.
, aktualisiert seinen Zustand innerhalb einer Abtastperiode und wiederholt dann die oben genannten Schritte zum nächsten Abtastzeitpunkt t+1.
03 Spieltheoretisches Modell des kooperativen Verhaltens von Fahrzeugen und explizite Darstellung durch Nachahmungslernen
In diesem Abschnitt wird das in diesem Artikel verwendete Leader-Follower-Spielmodell vorgestellt. Um die Online-Berechnung des spieltheoretischen Modells zu vereinfachen, wird Nachahmungslernen verwendet, um ein explizites Modell basierend auf neuronalen Netzen zu erhalten, um die Flugbahn der Reaktion des interaktiven Fahrzeugs online vorherzusagen und in das Verhalten des eigenen Fahrzeugs im MPC-basierten Gesamtverhalten überzugehen Flugbahnplanungsstrategie.
Theoretisches Modell des Leader-Follower-Spiels
In diesem Artikel betrachten wir ein parametrisches theoretisches Modell, das auf paarweisen Leader-Follower-Interaktionen basiert, um die kooperative Absicht des Fahrers und die daraus resultierenden Konsequenzen darzustellen. Das resultierende Fahrzeugverhalten wird als Leader bezeichnet -Follower-Spielmodell. In diesem Modell ist das Fahrzeug (oder der Fahrer), das sich entscheidet, vor dem anderen Fahrzeug voranzufahren, der Anführer des Paares, während das Fahrzeug, das sich entscheidet, dem anderen Fahrzeug nachzugeben, der Nachfolger des Paares ist. Führungskräfte und Follower nutzen unterschiedliche Entscheidungsstrategien. Dieses Leader-Follower-Spieltheoriemodell wurde ursprünglich in [32] vorgeschlagen. Dieses spieltheoretische Modell wird hier kurz besprochen, um seine Anwendung im Szenario der erzwungenen Autobahnzusammenführung vorzustellen.
stellt die Flugbahnen des Anführers und des Gefolgsmanns als bzw. dar, wobei und die realisierbare Flugbahnmenge des Anführers und des Gefolgsmanns ist. Nehmen Sie an, dass beide Parteien im Spiel eine Entscheidung getroffen haben, ihre kumulativen Belohnungen zu maximieren, die jeweils wie folgt aufgezeichnet werden:
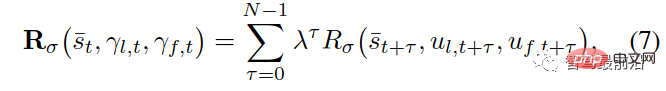
, wobei die Rolle im Spiel die Belohnungsfunktion des Anführers/ Follower und stellt den entsprechenden Steuereingang der Summe der beiden Trajektorien dar.
Konkret modellieren wir den interaktiven Entscheidungsprozess von Führungskräften und Followern wie folgt:
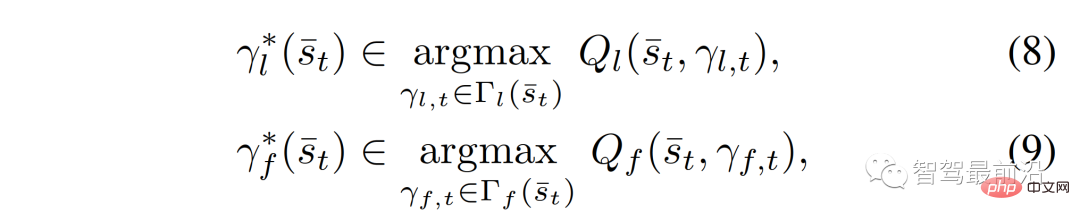
wobei 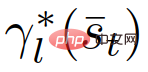 (anders als
(anders als 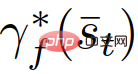 ) der Anführer ist (anders als Die optimale Flugbahn von der Follower) hängt vom aktuellen Verkehrsstatus ab,
) der Anführer ist (anders als Die optimale Flugbahn von der Follower) hängt vom aktuellen Verkehrsstatus ab,  und
und 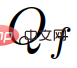 sind wie folgt definiert:
sind wie folgt definiert:
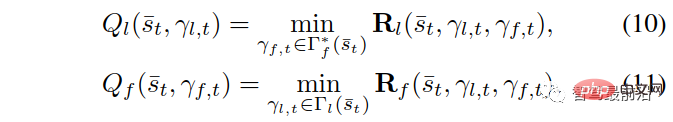
Welche
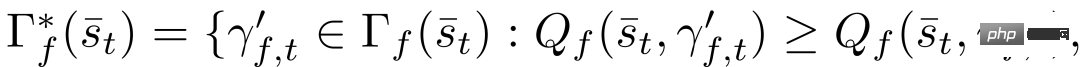
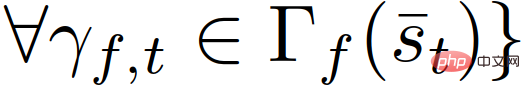 .
.
Das Entscheidungsmodell (8)-(11) bei der erzwungenen Zusammenführung kann wie folgt erklärt werden: Ein Follower stellt einen Fahrer dar, der nachgeben will. Aufgrund der Unsicherheit über die Handlungen anderer Fahrer entscheiden sich die Anhänger für eine Aktion, die ihre Worst-Case-Belohnung über (9) und (11) maximiert, vorausgesetzt, dass andere Fahrer frei handeln können. Ein Anführer stellt einen Fahrer dar, der die Absicht hat, weiterzufahren, vorausgesetzt, der andere Fahrer wird nachgeben. Daher verwendet der Anführer das Follower-Modell, um die Aktion eines anderen Fahrers vorherzusagen, und maximiert über (8) und (10) die eigene Belohnung des Anführers angesichts der vorhergesagten Aktion des Followers. Dieses Leader-Follower-Spielmodell ist teilweise vom Stackelberg-Spielmodell abgeleitet [38], lockert jedoch einige Annahmen, die nicht für Fahrerinteraktionen gelten. Für ein detaillierteres Verständnis des Leader-Follower-Spielmodells und seiner Wirksamkeit bei der Modellierung von Fahrerinteraktionen in Szenarien mit mehreren Fahrzeugen kann auf [32] verwiesen werden.
Bitte beachten Sie, dass dieses Modell nicht bedeutet, dass ein Führungsfahrzeug immer die Zusammenführung von Fahrzeugen hinter sich erzwingt oder dass ein Folgefahrzeug die Zusammenführung von Fahrzeugen immer vor sich erzwingt, wie in den beiden folgenden Beispielen das zusammenfahrende Fahrzeug darf vor dem Führungsfahrzeug einfädeln: 1) Das einfädelnde Fahrzeug befindet sich vor dem Führungsfahrzeug mit einem ausreichend großen Abstand, um ein sicheres Einfädeln zu ermöglichen. 2) Das zusammenfahrende Fahrzeug erreicht bald das Ende seiner Fahrspur. Da das Verlassen der Straße mit einer hohen Strafe verbunden ist (siehe Abschnitt 2-c), kann das eigene Fahrzeug wählen, solange das Auffahren des eigenen Fahrzeugs nicht zu einer Kollision führt (die Strafe für eine Kollision ist höher als für das Verlassen der Straße). vor dem entgegenkommenden Fahrzeug einzuordnen, um eine große Kollision zu vermeiden.
Das Obige zeigt, dass in unserem Entscheidungsmodell (8)-(11) die Rolle des Anführers und Gefolgsmanns nicht durch die räumliche Position des Fahrzeugs zugewiesen wird (der Anführer ist nicht unbedingt das vorausfahrende Fahrzeug). Darüber hinaus ermöglicht das Modell dem eigenen Fahrzeug, den Verkehrsfluss der Zielspur zu erzwingen: Wenn sich das eigene Auto der Zielspur nähert, wird es zunehmend das Zusammenführen vorziehen, um eine Strafe für das Verlassen der Straße zu vermeiden Das eigene Fahrzeug befindet sich mit allen interagierenden Fahrzeugen auf der Zielspur. Sie sind alle führend, oder sie ergreifen trotzdem die Einfädelungsmaßnahme, wenn die aktuelle Einfädellücke nicht groß genug ist und das Einfädeln nicht komfortabel genug ist. Die Modelle (8)–(11) zeigen, dass die Führungsidentität des interagierenden Fahrzeugs die nachfolgende Einfahrmotivation des zusammenfahrenden Fahrzeugs vorhersagen kann. Anschließend werden die zusammenfahrenden Fahrzeuge im Interesse ihrer eigenen Sicherheit und ihres Komforts ebenfalls langsamer und vergrößern den Abstand zwischen ihnen, um die Zusammenführung sicherzustellen.
Der Anführer, der die Spielstrategie explizit durch Nachahmungslernen vertritt
(8)-(11) Kann die Entscheidungsfindung und Flugbahn seines Autos basierend auf der Absicht des Fahrers und aktuellen Verkehrsstatusinformationen vorhersagen Das heißt, die optimale Aktionsstrategie des Anführers und die optimale Aktionsstrategie des Anhängers können durch (8)-(11) erhalten werden. Allerdings werden wiederholte Online-Berechnungen von (8)–(11) zeitaufwändig sein. Daher werden wir Nachahmungslernen zur Darstellung und expliziten Darstellung verwenden.
Siehe [39], wir verwenden die Darstellung des überwachten Lernens (insbesondere durch Nachahmungslernen).
Imitationslernen ist ein überwachtes Lernproblem, bei dem der Agent eine Strategie lernt, indem er das Verhalten von Experten beobachtet. Experten können menschliche oder künstliche Intelligenzagenten sein, und in unserer Arbeit wird durch (8)–(11) die Expertenstrategie erreicht.
Wir haben eine simulierte Strategie mithilfe des Algorithmus „Datensatzaggregation“ erhalten [40].
Unter diesen kann das allgemeine Lernziel des Datensatzaggregationsalgorithmus wie folgt beschrieben werden:
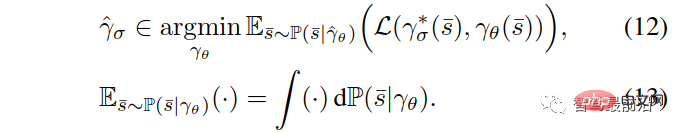
stellt die mit θ (Gewicht des neuronalen Netzwerks) parametrisierte Strategie dar, stellt die Verlustfunktion in Bezug auf Nachahmungslernen dar und „ Datensatzaggregation“ „Einzelheiten zum Algorithmus finden Sie unter [39] und [40].
Die Nachahmungslernstrategie des Lernens (8)–(11) kann die Entscheidungsfindung und den zukünftigen Entwicklungsverlauf seines Autos vorhersagen und gleichzeitig die kooperative Absicht des Fahrers verstehen. In einem bestimmten Verkehrsszenario kennen wir jedoch möglicherweise nicht im Voraus die Kooperationsabsichten anderer Fahrer, da die Absichten des Fahrers nicht nur von der Verkehrssituation (z. B. der relativen Position und Geschwindigkeit zwischen den beiden Fahrzeugen), sondern auch vom Fahrstil abhängen /Genre. Wir modellieren die Unsicherheit der Kooperationsabsichten anderer Fahrzeuge als latente Variablen, die zur Schätzung der Kooperationsabsichten anderer Fahrzeuge verwendet werden, und verwenden prädiktive Steuerungsmethoden, um optimale Trajektorien bei Planungs- und Steuerungsproblemen autonomer Fahrzeuge zu erhalten.
04 Entscheidungsfindung unter Unsicherheit der Kooperationsabsicht
Nachfolgend beschreiben wir den Highway Forced Merging-Entscheidungsfindungsalgorithmus unter Unsicherheit der Kooperationsabsicht, nämlich den Leader-Follower-Gamecontroller (LFGC). Während des erzwungenen Zusammenführungsprozesses erstellen wir eine Schätzung der Kooperationsabsichten anderer Fahrer, wie in diesem Abschnitt beschrieben, auf deren Grundlage wir (6) als paarweise interaktive Steuerungsstrategie für mehrere Fahrzeuge modellieren.
Abschätzung der kooperativen Absicht interagierender Fahrzeuge
Verwendung eines geführten Follower-Spiels, Verhaltensmodellierung basierend auf der kooperativen Absicht anderer Fahrzeugführer. Fahrzeuge, die nachgeben, werden im Spiel als Gefolgsleute modelliert, und Fahrzeuge, die weiterfahren (ohne nachzugeben), werden als Anführer modelliert. Das heißt, die kooperative Absicht des interaktiven Fahrzeugs kann durch Abschätzen seiner Rolle im Leader-Follower-Spiel abgeschätzt werden.
Um dies zu erreichen, berücksichtigen wir das Verkehrsdynamikmodell (2) und die optimalen Aktionen des Leaders oder Followers (8) und (9). Aus der Perspektive des Selbstfahrzeugs spielt das interaktive Fahrzeug ein Leader-Follower-Spiel, und das dynamische Verkehrsmodell kann als
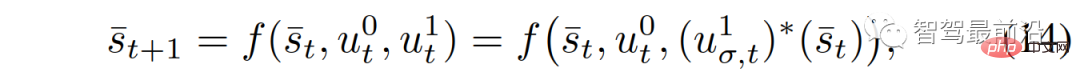
geschrieben werden, wobei 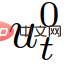 die Kontrolle des Selbst ist -Fahrzeug, und
die Kontrolle des Selbst ist -Fahrzeug, und 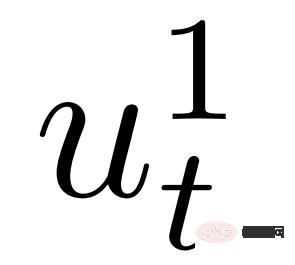 ist die Interaktion. Die Kontrolle über das Fahrzeug wird durch das Leader-Follower-Spiel erlangt,
ist die Interaktion. Die Kontrolle über das Fahrzeug wird durch das Leader-Follower-Spiel erlangt,  {Leader, Follower} stellt den Follower oder Anführer dar und
{Leader, Follower} stellt den Follower oder Anführer dar und 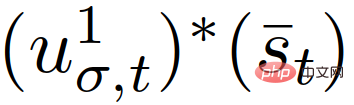 die erste Steuereingabe entspricht
die erste Steuereingabe entspricht 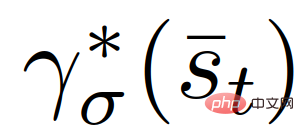 in (8) (9) die optimale Flugbahn. Jetzt ist die einzige Eingabe zu (14) die Steuerung des eigenen Autos
in (8) (9) die optimale Flugbahn. Jetzt ist die einzige Eingabe zu (14) die Steuerung des eigenen Autos  .
.
Angesichts der Tatsache, dass die Entscheidungsfindung anderer Autos in der Realität nicht unbedingt der aus (8) und (9) berechneten optimalen Strategie folgt, wird Gaußsches Rauschen hinzugefügt, vorausgesetzt, das System funktioniert gemäß (14). :
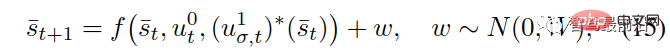
wo ist das additive Gaußsche Rauschen mit Mittelwert und Kovarianz von 0.
Nehmen Sie an, dass das Selbstauto eine vorherige Überzeugung über σ hat, ausgedrückt als {Anführer, Anhänger}. Dann basierend auf allen bisherigen Verkehrszuständen und allen vom eigenen Auto ergriffenen Maßnahmen
Das Selbstfahrzeug muss eine nachträgliche Überzeugung über die Führungs- oder Mitläuferrolle des interaktiven Fahrzeugs berechnen oder aufrechterhalten, 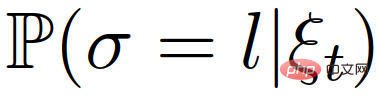 .
.
Unter Verwendung des in [41] vorgeschlagenen Hybridschätzalgorithmus kann der bedingte hintere Glaube an die Führungs- oder Followerrolle des interaktiven Fahrzeugs berechnet werden.
Konkret kann die Identifizierung der Führungs- oder Followerrolle des interaktiven Fahrzeugs wie folgt ausgedrückt werden:
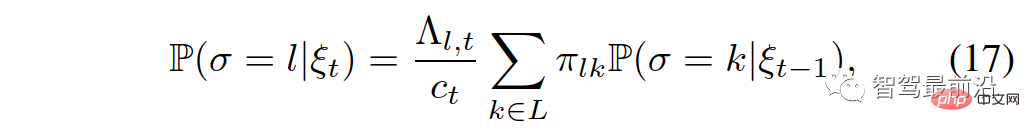
wobei  die bedingte Wahrscheinlichkeit ist;
die bedingte Wahrscheinlichkeit ist;  die Rolle des handelnden Fahrzeugs von
die Rolle des handelnden Fahrzeugs von 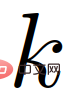 Die Übergangswahrscheinlichkeit von zu
Die Übergangswahrscheinlichkeit von zu 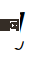 ;
; 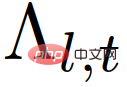 ist die Wahrscheinlichkeitsfunktion des Action-Car-Charakters
ist die Wahrscheinlichkeitsfunktion des Action-Car-Charakters 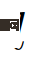 , die definiert ist als:
, die definiert ist als:
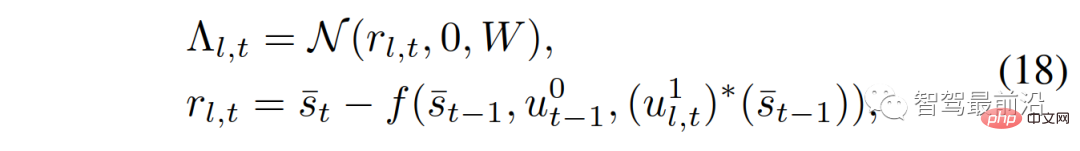
wobei, 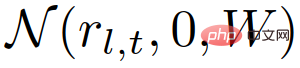 ist die Wahrscheinlichkeit der Normalverteilungsdichtefunktion, der Mittelwert ist 0 und die Kovarianz W wird bei
ist die Wahrscheinlichkeit der Normalverteilungsdichtefunktion, der Mittelwert ist 0 und die Kovarianz W wird bei  bewertet;
bewertet; 
ist eine Normalisierungskonstante.
Angenommen, dass die Rolle des interagierenden Fahrzeugs während der Zusammenführung unverändert bleibt, d kann mit der folgenden Gleichung aktualisiert werden: 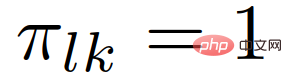

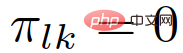
wobei 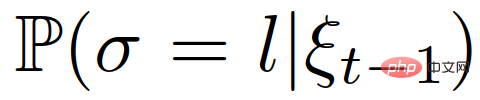 der vorherige Glaube an die Rolle des Anführers oder Anhängers des interaktiven Fahrzeugs ist.
der vorherige Glaube an die Rolle des Anführers oder Anhängers des interaktiven Fahrzeugs ist.
Steuerungsstrategie für die Interaktion mehrerer Fahrzeuge
#🎜🎜 #Bei starkem Verkehr können sich mehrere Fahrzeuge auf der Autobahn befinden, die das Einfädeln Ihres Fahrzeugs behindern, wie in Abbildung 1 dargestellt. Eine Lösung mit geringer Komplexität besteht darin, dass das eigene Fahrzeug nur Interaktionen mit dem ersten Fahrzeug berücksichtigt und dann mit der Interaktion mit dem zweiten Fahrzeug beginnt, nachdem sich das erste Fahrzeug entfernt hat. Dies kann jedoch zu einer Verzögerung bei der Einschätzung der Absichten des nachfolgenden Fahrzeugs führen, wodurch das eigene Fahrzeug die Möglichkeit zum Einfädeln verliert.
Eine andere Lösung besteht darin, mit mehreren Fahrzeugen gleichzeitig zu interagieren. Zu diesem Zeitpunkt muss ein Modell erstellt werden, um das Verhalten des interaktiven Fahrzeugs vorherzusagen. Obwohl das in Abschnitt 3 beschriebene Leader-Follower-Spiel für zwei Spieler durch die Berücksichtigung mehrstufiger Entscheidungshierarchien auf ein Leader-Follower-Spiel für mehrere Spieler erweitert werden kann, wird die Modellkomplexität mit zunehmender Spielerzahl exponentiell zunehmen. Bei mehr als drei Spielern ist es schwierig, das Stackelberg-Gleichgewicht zu erreichen [42]. Daher schlagen wir eine rechnerisch nachvollziehbare Methode vor, um das Framework durch die Berücksichtigung paarweiser Interaktionen auf Interaktionen mit mehreren Fahrzeugen zu erweitern.
Wenn es m interagierende Fahrzeuge gibt, berücksichtigen wir die paarweise Interaktion des eigenen Fahrzeugs und jedes interagierenden Fahrzeugs und konstruieren dann m, das das eigene Fahrzeug und den Verkehr enthält Der Zustand des k-ten anderen Fahrzeugzustands wird ausgedrückt als, und das dynamische Modell jedes einzelnen wird durch die folgende Formel angegeben:
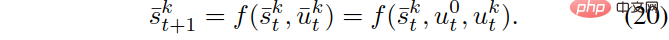 # 🎜 🎜#
# 🎜 🎜#
In ähnlicher Weise können wir
{Leader, Follower} verwenden, um den paarweisen Anführer des k-ten interagierenden Fahrzeugs darzustellen. Die Rolle eines Follower oder Follower, und 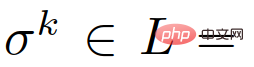 stellt die Menge aller vorherigen gepaarten Verkehrszustände und Aktionen des eigenen Fahrzeugs dar, also
stellt die Menge aller vorherigen gepaarten Verkehrszustände und Aktionen des eigenen Fahrzeugs dar, also 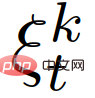 # 🎜 🎜#
# 🎜 🎜#
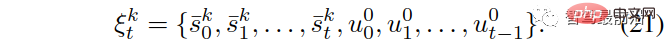
, 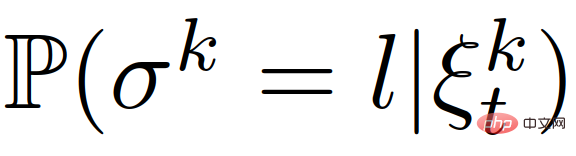
 {Führer, Anhänger}. Die MPC-basierte Kontrollstrategie in (6) kann wie folgt umformuliert werden:
{Führer, Anhänger}. Die MPC-basierte Kontrollstrategie in (6) kann wie folgt umformuliert werden:
#🎜🎜 # 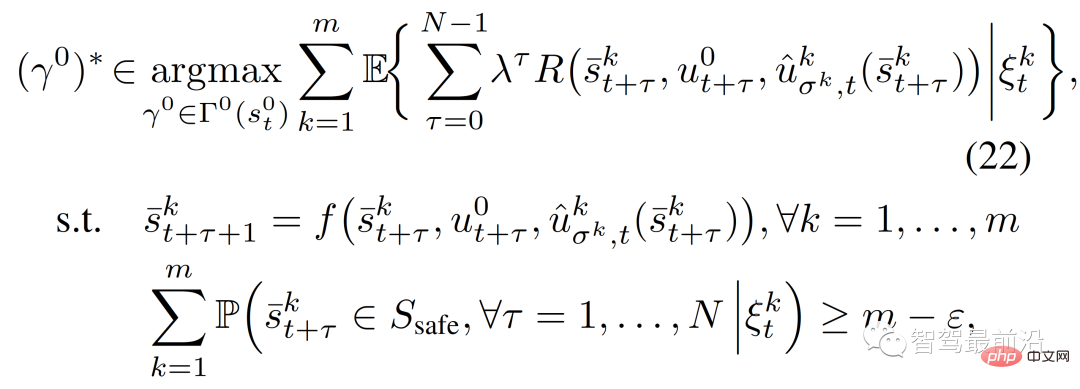
der erste Steuereingang, der der Flugbahn der Trainingsstrategie 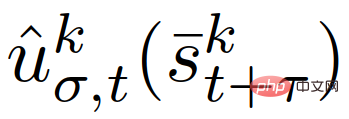 in entspricht (12) ε∈[0,1] stellt das (vom Benutzer angegebene) erforderliche Wahrscheinlichkeitsniveau für die Erfüllung von Einschränkungen dar.
in entspricht (12) ε∈[0,1] stellt das (vom Benutzer angegebene) erforderliche Wahrscheinlichkeitsniveau für die Erfüllung von Einschränkungen dar. 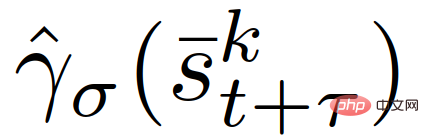 Der Erwartungswert in der Zielfunktion kann gemäß (23) gelöst werden;
Der Erwartungswert in der Zielfunktion kann gemäß (23) gelöst werden;
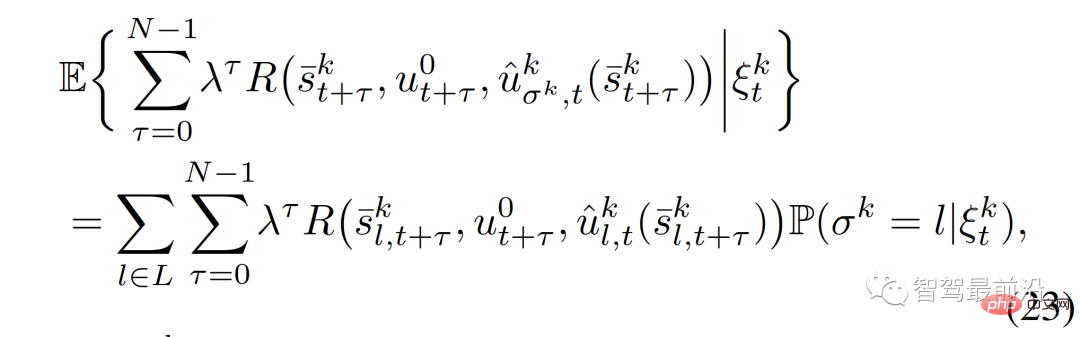
wobei 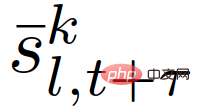 der vorhergesagte Verkehrszustand für ein gegebenes interagierendes Fahrzeug ist, dessen Rolle
der vorhergesagte Verkehrszustand für ein gegebenes interagierendes Fahrzeug ist, dessen Rolle 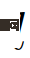 ist, und die letzte Einschränkung in (22) übergeben werden kann,
ist, und die letzte Einschränkung in (22) übergeben werden kann,
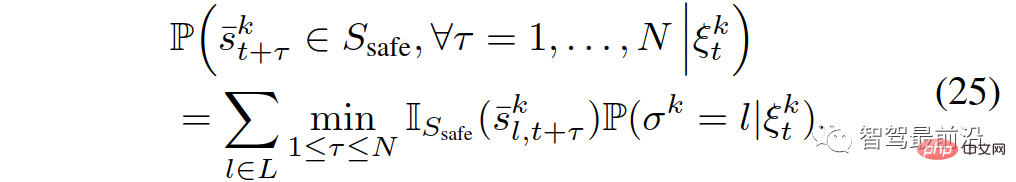
wobei 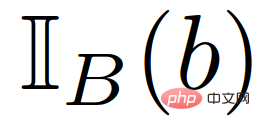 die Indikatorfunktion von b in Satz B ist. Beachten Sie, dass die letzte Einschränkung in (22) die folgende Bedingung erzwingt:
die Indikatorfunktion von b in Satz B ist. Beachten Sie, dass die letzte Einschränkung in (22) die folgende Bedingung erzwingt:
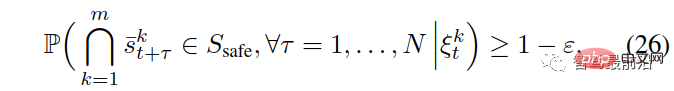
, was bedeutet, dass die Wahrscheinlichkeit, dass ein Paar von Interaktionen in einen unsicheren Zustand eintritt (z. B. Kollision und Verlassen der Straßenbegrenzung), kleiner als ε ist.
Um (26) abzuleiten, stellen wir zuerst das Ereignis 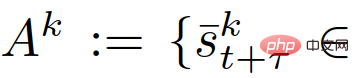
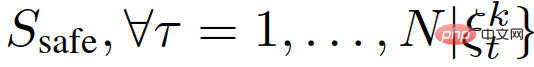 dar, dann
dar, dann
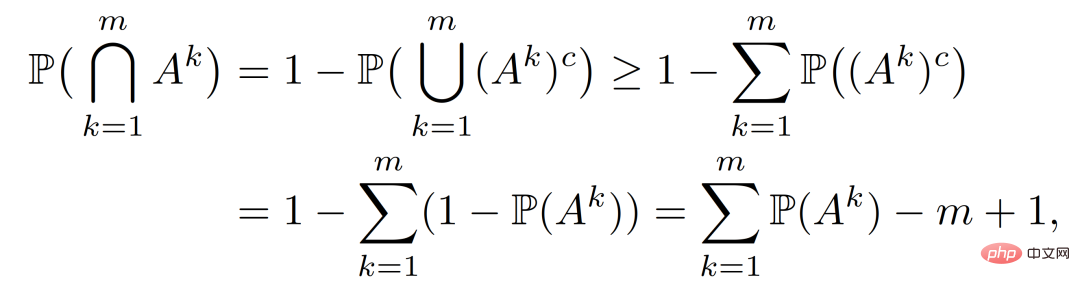
und wenden dann die letzte Einschränkung in (22) an, wir erhalten.
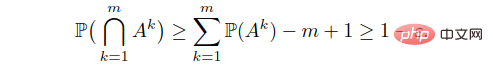
Der Hauptunterschied zwischen (6) und (22) ist:
1) Die Werte in (6) sind unbekannt, während sie in (22) auf der Grundlage der Trainingsstrategie des Nachahmungslernens erhalten werden
2) Ändern Sie die Maximierung der kumulativen Belohnung in (6) in die Maximierung der erwarteten kumulativen Belohnung in (22), um die probabilistischen Überzeugungen der Führungs-/Follower-Rolle des interaktiven Fahrzeugs zu erklären; Die erwartete kumulative Belohnung wird in die Summe der erwarteten Belohnungen aller paarweisen Interaktionen geändert, um das unsichere Verhalten mehrerer Fahrzeuge zu berücksichtigen (zur Vereinfachung der Berechnung).
4) Die harte Einschränkung wird zu einer Wahrscheinlichkeitsbeschränkung mit ε∈ [0, 1] ist ein Parameter.
Der Entscheidungsalgorithmus läuft wie folgt ab: Zum Abtastzeitpunkt t misst das Ego-Fahrzeug den aktuellen Status jedes Satzes interagierender Paare und fügt ihn zusammen mit den vorherigen Steuereingaben dem Beobachtungsvektor 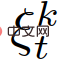 hinzu. Die Überzeugungen über die Führungs- oder Mitläuferrolle jedes Fahrzeugs werden gemäß (19) aktualisiert. Anschließend wird unter Verwendung der MPC-basierten Steuerstrategie (22) die optimale Flugbahn
hinzu. Die Überzeugungen über die Führungs- oder Mitläuferrolle jedes Fahrzeugs werden gemäß (19) aktualisiert. Anschließend wird unter Verwendung der MPC-basierten Steuerstrategie (22) die optimale Flugbahn 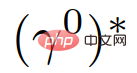 durch Durchsuchen aller in Abschnitt 2-D eingeführten Flugbahnen ermittelt, und das Ego-Fahrzeug aktualisiert seinen Zustand durch Anwenden der ersten Steuereingabe innerhalb eines Abtastzeitraums. Der gesamte Vorgang wird bei der nächsten Probenentnahme wiederholt.
durch Durchsuchen aller in Abschnitt 2-D eingeführten Flugbahnen ermittelt, und das Ego-Fahrzeug aktualisiert seinen Zustand durch Anwenden der ersten Steuereingabe innerhalb eines Abtastzeitraums. Der gesamte Vorgang wird bei der nächsten Probenentnahme wiederholt.
Es ist zu beachten, dass die Kontrollstrategie (22) aus folgenden Gründen „interaktionsbewusst“ ist:
1) Sie basiert auf dem Leader-Follower-Spieltheoriemodell (8)-(11) das verschiedene vorhersagt Die Flugbahn seines Autos unter interaktiver Absicht.
2) Diese Vorhersagen basieren alle auf einem geschlossenen Regelkreis. Insbesondere entsprechend der unterschiedlichen Trajektorienplanung des eigenen Fahrzeugs ist auch die Trajektorienvorhersage anderer Fahrzeuge mit bestimmten Absichten unterschiedlich. Diese Situation liegt daran, dass das vorhergesagte Verhalten anderer Fahrzeuge vom Verkehrszustand abhängt und der vorhergesagte Verkehrszustand von der geplanten Flugbahn des eigenen Fahrzeugs abhängt. 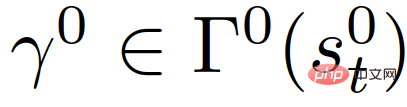
. Gleichzeitig wird die Absicht des anderen Autos anhand seines bisherigen Interaktionsverhaltens abgeschätzt. 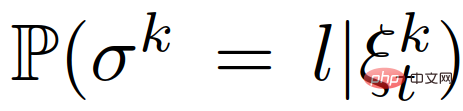
In diesem Abschnitt zeigen wir die Verifizierungsergebnisse des Leader-Follower-Gamecontrollers (LFGC), angewendet auf das Problem der erzwungenen Zusammenführung autonomer Fahrzeuge. Wir betrachten insbesondere drei Simulationsüberprüfungen, bei denen LFGC davon ausgeht, dass das interagierende Fahrzeug ein Leader-Follower-Spiel mit dem eigenen Fahrzeug spielt, und ihre Leader-/Follower-Rollen im Spiel abschätzt. Wir gehen außerdem davon aus, dass das eigene Fahrzeug, sobald es in eine Situation mit einem erzwungenen Spurwechsel eintritt, den Blinker verwendet, um sich auf die Fahrspur auszurichten, seine Absicht zum Einfädeln ankündigt und den Prozess des erzwungenen Einfädelns startet. Daher sind sich andere miteinander interagierende Fahrzeuge der Zusammenfahrabsicht des eigenen Fahrzeugs bewusst und reagieren entsprechend.
Wir validieren LFGC zunächst in einem Leader-Follower-Spiel mit interaktiven Fahrzeugen, die entweder von einem Leader oder einem Follower gesteuert werden. Anschließend haben wir LFGC mit interaktiven Fahrzeugen getestet, die von anderen Fahrertypen oder echten Verkehrsdaten gesteuert werden. Darüber hinaus haben wir den Fall getestet, bei dem ein interaktives Fahrzeug (IDM) von einem intelligenten Fahrermodell gesteuert wurde und das interaktive Fahrzeug den tatsächlichen Verkehrsdaten des US Highway 101 von der Next Generation Simulation Site folgte [34]. Unsere Simulationen wurden auf der MATLAB R2019a-Plattform auf einem PC mit Intel Xeon E3-1246 v3 @ 3,50 GHz CPU und 16 GB Speicher durchgeführt.
Interaktives Fahrzeug mit Leader-Follower-Modell
Zuerst verwenden wir Leader/Follower, um das interaktive Fahrzeug zu simulieren und zu steuern, um LFGC zu testen. Das von uns betrachtete Szenario ist in Abbildung 4 dargestellt. Das autonome Fahrzeug (blau) auf der Beschleunigungsspur muss vor dem Ende der Beschleunigungsspur auf die Autobahn einfahren, während sich derzeit viele andere Fahrzeuge (rot, rosa, grün) auf der Autobahn befinden Autobahn. Fahren auf der Autobahn. Wie in Abbildung 4 dargestellt, startet das eigene Fahrzeug den erzwungenen Einfädelvorgang, indem es in Richtung der Fahrbahnmarkierungen abweicht und den Blinker blinkt. In diesem Fall muss das autonome Fahrzeug mit anderen Fahrzeugen interagieren, um eine sichere Zusammenführung zu erreichen.
Abbildung 4 LFGC-Verifizierungsszenendiagramm des Anführers/Followers, der das interaktive Fahrzeug im erzwungenen Zusammenführungsszenario auf der Autobahn steuert
Nach dem Test kann das Selbstfahrzeug = die Absicht des interaktiven Fahrzeugs (das) korrekt identifizieren Das heißt, es kann die Interaktion (andere Autos sind Anführer/Follower) richtig aufteilen sind drei Anführer;
(b) Das andere Auto ist 1 Anführer (Fahrzeug 1) und 2 Anhänger (Fahrzeug 2 und 3); 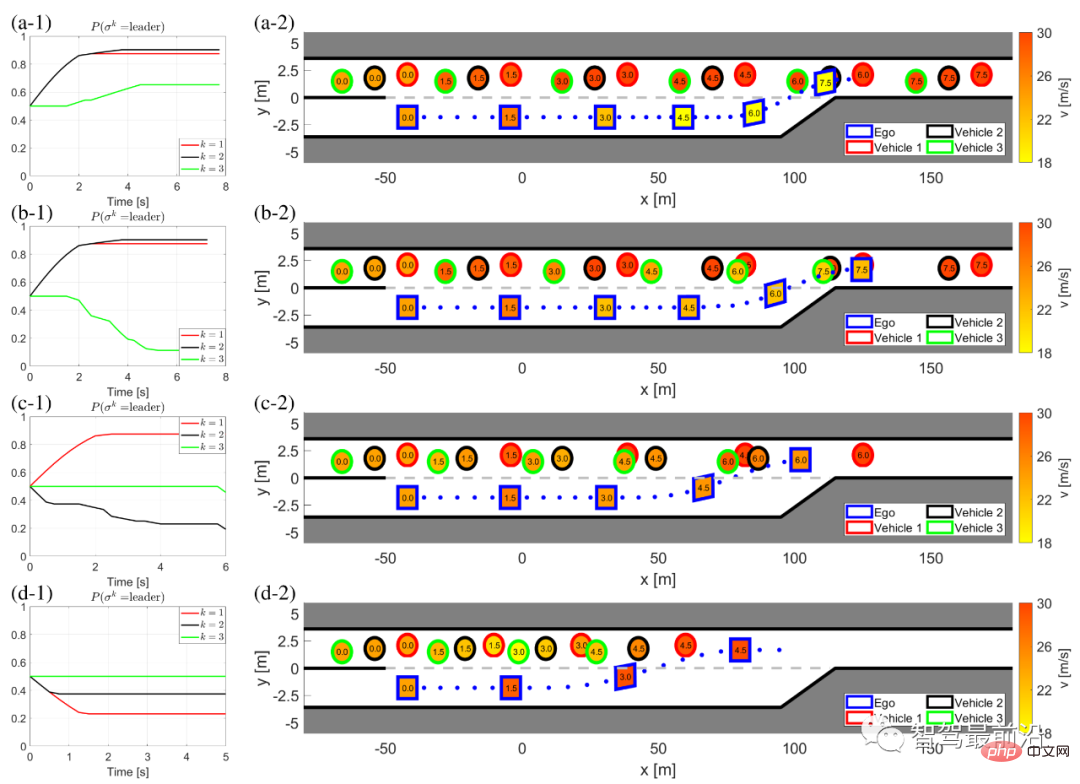
(c) Das andere Auto ist zwei Anführer (Fahrzeug 1 und 3) 2) und ein Follower (Fahrzeug 3); (d) Das andere Auto hat drei Follower.
Die linke Spalte (a-1) bis (d-1) zeigt den Glauben des Selbstautos an den Anführer seines Autos im Spiel. Die rechten Spalten (a-2) bis (d-2) zeigen die zeitlichen Verlaufsergebnisse des Verhaltens des eigenen Fahrzeugs und anderer Fahrzeuge während dieses erzwungenen Zusammenführungsprozesses. Insbesondere in der rechten Spalte unterscheidet die Farbe der Grenzlinie jedes Blocks verschiedene Fahrzeuge, die Zahl im Block stellt die Zeit in Sekunden dar, die Farbe jedes Blocks beschreibt die Fahrzeuggeschwindigkeit zu diesem Zeitpunkt und die blaue gepunktete Linie stellt dar die Flugbahn des eigenen Fahrzeugs. Beachten Sie, dass die Fahrzeuge 1-3 die gleiche Längsposition haben. Zur besseren Unterscheidung wurde der Abbildung ein gewisser Längsversatz hinzugefügt.
Für LFGC beträgt der Planungsbereich N = 4 und der Zufallsbeschränkungsparameter beträgt ε = 0,1. Beachten Sie, dass ein größeres N zu einer besseren Langzeitleistung, aber auch zu längeren Rechenzeiten führen kann, während ein kleineres N den unmittelbaren Nutzen hervorheben kann und daher in vielen Fällen nicht kombiniert werden kann. Für die in diesem Artikel betrachteten erzwungenen Autobahnzusammenführungen muss N im Allgemeinen so gewählt werden, dass es die Dauer des Spurwechsels überschreitet (d. h.
).
Abbildung 5(a) zeigt die Ergebnisse, wenn das Ego-Auto mit drei Anführern interagiert. Das eigene Fahrzeug ist in der Lage, die Absicht der interagierenden Fahrzeuge zu erfassen, das heißt, alle Fahrzeuge werden mit größerer Wahrscheinlichkeit zu Anführern im Spiel, wie in Abbildung 5(a-1) dargestellt. Nachdem das eigene Fahrzeug diese Informationen erhalten hat, beschließt es, nach t = 1 [s] langsamer zu werden und wartet auf die Zusammenführung, nachdem alle interagierenden Fahrzeuge vorbeigefahren sind.
Wenn das Self-Car mit einem Anführer (Fahrzeug 1) und zwei Followern (Fahrzeuge 2 und 3) interagiert, erkennt das Self-Car die Absicht des interagierenden Fahrzeugs korrekt, wie in Abbildung 5(b-1) dargestellt. . Dann, nach t = 1 [s], beginnt das eigene Fahrzeug abzubremsen und führt erfolgreich zwischen Fahrzeug 1 und Fahrzeug 2 zusammen, wie in Abbildung 5(b-2) dargestellt. Wie in Abbildung 5 dargestellt, ist (c) das Ergebnis der Interaktion zwischen dem eigenen Fahrzeug und zwei Anführern (Fahrzeuge 1 und 2) und einem Gefolgsmann (Fahrzeug 3).
In diesem Fall beobachtet das Ego-Fahrzeug, wie die Fahrzeuge 1 und 2 beschleunigen, ohne nachzugeben, sodass das Ego-Fahrzeug beschließt, langsamer zu werden und zwischen den Fahrzeugen 2 und 3 zusammenzuführen. Wir haben auch Tests durchgeführt, bei denen das Selbstauto mit drei Followern interagierte. Die Ergebnisse sind in Abbildung 5(d) dargestellt. Das Selbstauto beobachtete alle Fahrzeuge, die eine Absicht erzeugten, beschleunigte und fuhr vor allen interagierenden Fahrzeugen zusammen. Die durchschnittliche Rechenzeit zur Lösung von (22) beträgt 0,182 [s] in jedem Zeitschritt. 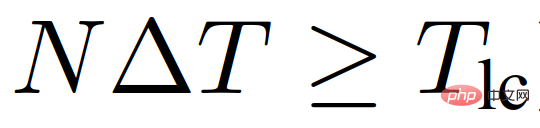
Das andere Auto verwendet das IDM-Modell
Interaktionstyp
Die in Abschnitt 5-A gezeigten Verifizierungsergebnisse gehen davon aus, dass andere Autos Entscheidungen auf der Grundlage des Leader-Follower-Spiels treffen. LFGC schätzt die Rolle anderer Fahrer im Spiel ein und trifft entsprechende Entscheidungen. Dies bedeutet, dass sich die Umgebung in Abschnitt 5-A wie von LFGC erwartet verhält. Allerdings kann das tatsächliche Verhalten anderer Fahrer von der Politik des Leader-Follower-Spiels abweichen. Daher untersuchen wir weiter, wie das Framework reagiert, wenn andere Fahrzeuge ein Intelligentes Fahrermodell (IDM) verwenden.
In diesem Abschnitt verwenden Sie IDM, um andere Autos zu steuern und mit Ihrem eigenen Auto zu interagieren. Das Ego-Fahrzeug wird immer noch vom LFGC gesteuert und versucht, die Absichten der interagierenden Fahrzeuge abzuschätzen, indem es ihre entsprechenden Führungs- oder Follower-Rollen abschätzt. IDM ist ein zeitkontinuierliches Fahrzeugverfolgungsmodell, definiert durch (27) bis (29) [43].
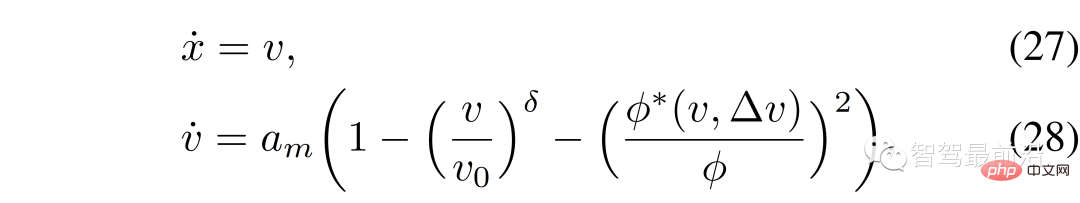
wobei 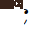 die Längsgeschwindigkeit ist;
die Längsgeschwindigkeit ist; 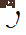 die erwartete Geschwindigkeit des Fahrzeugs ist folgende Distanz,
die erwartete Geschwindigkeit des Fahrzeugs ist folgende Distanz, 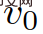 ist das Zielfahrzeug. Die Position von
ist das Zielfahrzeug. Die Position von 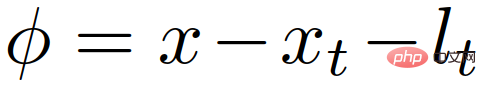
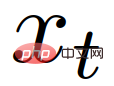 Daunter sind
Daunter sind  die Parameter des IDM-Modells. Die physikalische Interpretation dieser Parameter ist die maximale Beschleunigung
die Parameter des IDM-Modells. Die physikalische Interpretation dieser Parameter ist die maximale Beschleunigung 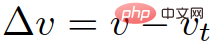 , der minimale Fahrzeugfolgeabstand
, der minimale Fahrzeugfolgeabstand 
, die gewünschte Zeit T und die angenehme Verzögerung b. Wir haben das in Abbildung 6 dargestellte Szenario als Validierungstest betrachtet. In Abbildung 6 fährt allen Fahrzeugen ein weiteres Fahrzeug (schwarzes Fahrzeug 4) voraus, das mit konstanter Geschwindigkeit fährt. Das Ego-Fahrzeug ist immer noch dasselbe wie die V-A-Sektion und wird vom LFGC gesteuert, was bedeutet, dass es aus der Sicht des Ego-Fahrzeugs ein Anführer-Folger-Spiel mit allen interagierenden Fahrzeugen spielt. Diese drei interagierenden Fahrzeuge (Fahrzeug 1 bis 3) werden von IDM gesteuert und folgen dem vorausfahrenden Fahrzeug (Fahrzeug 4) oder dem eigenen Fahrzeug mit einem bestimmten Zeitvorlauf t. Die Parameter des IDM-Modells sind in Tabelle 1 aufgeführt. Beachten Sie, dass das eigene Fahrzeug Fahrzeug 4 als Umgebungsfahrzeug behandelt und davon ausgeht, dass es mit konstanter Geschwindigkeit fährt. 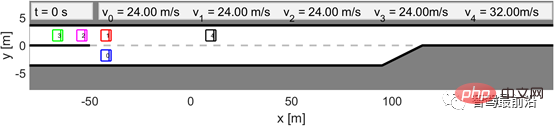
Abbildung 6: Wenn das andere Auto dem IDM folgt, verwendet das eigene Auto LFGC, um die erzwungene Zusammenführungsszene abzuschließen
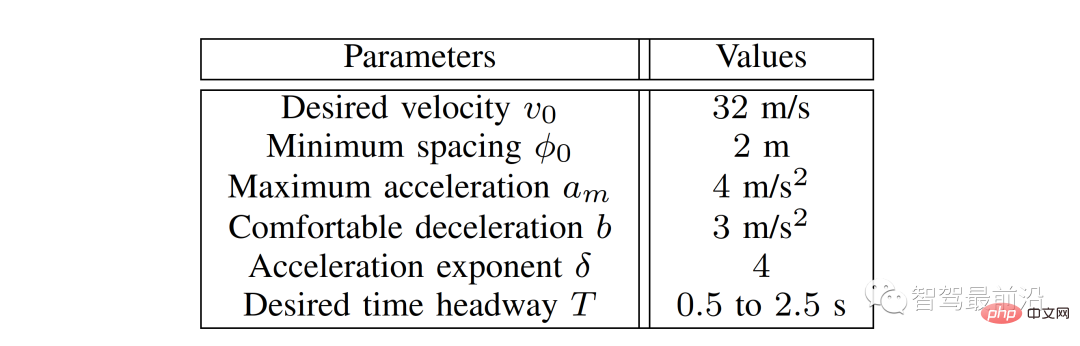
Tabelle 1 Parameter des intelligenten Fahrermodells.
Abbildung 7 zeigt die Ergebnisse, wenn das eigene Fahrzeug mit anderen von IDM gesteuerten Fahrzeugen mit unterschiedlichen Zielfahrzeugen und unterschiedlichen Wunschzeiten interagiert.
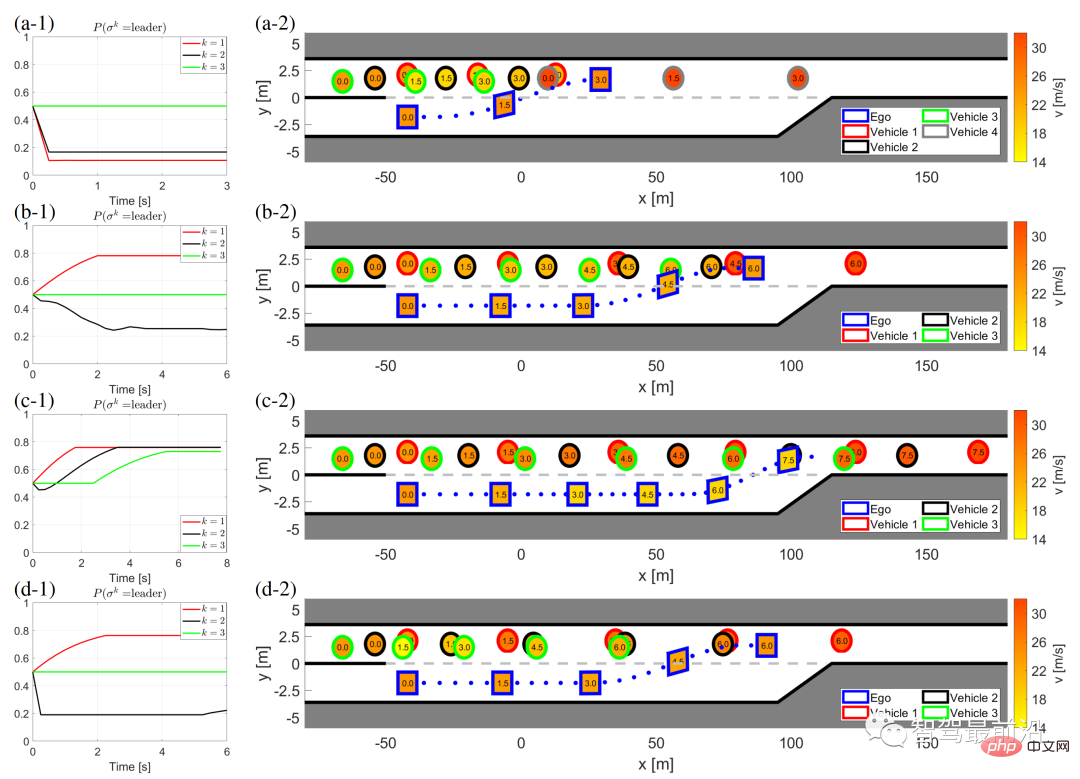
Abbildung 7: LFGC-Interaktionsergebnisse für andere Fahrzeuge mit unterschiedlichen Zielen und erwarteten Zeiten, gesteuert durch IDM
(a) Fahrzeug 1 generiert (dem eigenen Fahrzeug folgend) einen Zeitfortschritt T = 1 [s], Fahrzeug 2 und Fahrzeug 3 folgen T = 0,5 [s];
(b) Fahrzeug 2 erzeugt (dem eigenen Fahrzeug folgend) T=0,5[s], Fahrzeuge 1 und 3 folgen dem vorherigen Fahrzeug T = 0,5 [s];
(c) Alle Fahrzeuge folgen dem Vorderfahrzeug mit T = 0,5 [s] (d) Alle Fahrzeuge folgen dem Vorderfahrzeug mit T = 1,5 [s].
Die linke Spalte (a-1) bis (d-1) zeigt den Glauben des Selbstautos an den Anführer seines Autos im Spiel. Die rechten Spalten (a-2) bis (d-2) zeigen die zeitlichen Verlaufsergebnisse des Verhaltens von sich selbst und anderen Fahrzeugen während dieses erzwungenen Fusionsprozesses. Insbesondere in der rechten Spalte unterscheidet die Farbe der Grenzlinie jedes Blocks verschiedene Fahrzeuge, die Zahl im Block stellt die Zeit in Sekunden dar, die Farbe jedes Blocks beschreibt die Fahrzeuggeschwindigkeit zu diesem Zeitpunkt und die blaue gepunktete Linie stellt dar die Flugbahn des eigenen Fahrzeugs.
In Abbildung 7(a) beabsichtigt das erste interaktive Fahrzeug (Fahrzeug 1), seinem eigenen Fahrzeug nachzugeben, und entscheidet sich daher dafür, seinem eigenen Fahrzeug zu folgen, das in 1 Sekunde vorankommt, während die letzten beiden interaktiven Fahrzeuge dem eigenen Fahrzeug folgen -Fahrzeug, das in 0,5 Sekunden vorausfährt. Wie aus Abbildung 7 (a-1) ersichtlich ist, geht das Auto selbst davon aus, dass Fahrzeug 1 mit hoher Wahrscheinlichkeit ein Anhänger im Spiel wird, und entscheidet sich dafür, vor Fahrzeug 1 zusammenzufahren, wie in Abbildung 7 (a) dargestellt -2).
Abbildung 7(b) zeigt eine andere Situation, das heißt, das erste interaktive Fahrzeug (Fahrzeug 1) rückt um 0,5 vor, und das zweite interaktive Fahrzeug beabsichtigt, seinem eigenen Fahrzeug nachzugeben und rückt um 0,5 vor, um seinem eigenen Fahrzeug zu folgen. In diesem Fall hat Fahrzeug 1 aus Sicht des eigenen Fahrzeugs eine höhere Wahrscheinlichkeit, der Anführer im Spiel zu werden, und Fahrzeug 2 hat eine höhere Wahrscheinlichkeit, ein Mitläufer im Spiel zu werden Eigenfahrzeug Das Auto ist erfolgreich vor Fahrzeug 2 eingefahren.
Die beiden anderen Nicht-Nachgiebigkeitsfälle sind in Abbildung 7(c) und (d) dargestellt. Abbildung 7(c) zeigt die Ergebnisse für alle interagierenden Fahrzeuge, die dem vorausfahrenden Fahrzeug folgen. Aus Sicht des Selbstfahrzeugs ist es wahrscheinlicher, dass alle interagierenden Fahrzeuge zu Anführern im Spiel werden, sodass das Selbstfahrzeug erfolgreich zusammengeführt werden kann, nachdem alle Fahrzeuge vorbeigefahren sind.
In Abbildung 7(d) bewegen sich alle interagierenden Fahrzeuge mit einer Geschwindigkeit von 1,5 Sekunden vorwärts. In diesem Fall stellt das eigene Fahrzeug fest, dass sich Fahrzeug 2 konservativ verhält, und geht davon aus, dass Fahrzeug 2 eine höhere Wahrscheinlichkeit hat, ein Mitläufer im Spiel zu werden. Daher gelingt die Fusion des eigenen Fahrzeugs zwischen Fahrzeug 1 und Fahrzeug 2. Die durchschnittliche Rechenzeit zur Lösung von (22) beträgt 0,198 [s] in jedem Zeitschritt.
Andere Fahrzeuge folgen echten Verkehrsdaten
Wir haben LFGC in Leader-Follower-Spielen an anderen Fahrzeugen mit Leader/Follower-Antrieb und IDM-Modellen getestet. Wir wollten die Leistung des Controllers anhand realer Verkehrsdaten weiter testen. Konkret verwenden wir den Verkehrsdatensatz US Highway 101 von der Next Generation Simulation (NGSIM)-Website [34], der von der US Federal Highway Administration gesammelt wird und als eine der größten öffentlich zugänglichen Quellen für naturalistische Fahrdaten gilt. Der Datensatz des US Highway 101 wurde in der Literatur ausführlich untersucht [44], [45], [46].
Genauer gesagt betrachten wir einen Teil des US-101-Verkehrsdatensatzes, der 30 Minuten Fahrzeugverläufe auf dem US-101-Highway enthält. Der Zeitraum reicht von 7:50 bis 8:20 Uhr morgens und stellt den Stau vor und nach der morgendlichen Hauptverkehrszeit dar. Der Datensatz enthält Positions- und Geschwindigkeitstrajektorien sowie Fahrzeugabmessungen von etwa 6000 Fahrzeugen, wobei die Informationen alle 0,1 [s] aufgezeichnet werden. Eine Draufsicht auf den Abschnitt des US Highway 101, der für die Datenerfassung genutzt wird, ist in Abbildung 8 dargestellt. Das Untersuchungssegment umfasste die fünf Hauptspuren der Autobahn, eine Auffahrt zur Autobahn, eine Ausfahrt von der Autobahn und eine Nebenspur für die Ein- und Ausfahrt auf die Autobahn.
Wie in [47] erläutert, enthält der US101-Datensatz aufgrund der Videoanalyse und der numerischen Differenzierung eine erhebliche Menge an Rauschen. Um diesen Mangel zu beheben, verwenden wir den Savitsky-Gorey-Filter [48], um die Position des Fahrzeugs zu glätten und seine entsprechende Geschwindigkeit zu aktualisieren. Der Savitzky-Golay-Filter schneidet beim US101-Datensatz mit einer Zeitfensterlänge von 21 gut ab [45]. Eine ursprüngliche Fahrzeugtrajektorie und die entsprechende geglättete Fahrzeugtrajektorie sind in Abbildung 9 dargestellt.
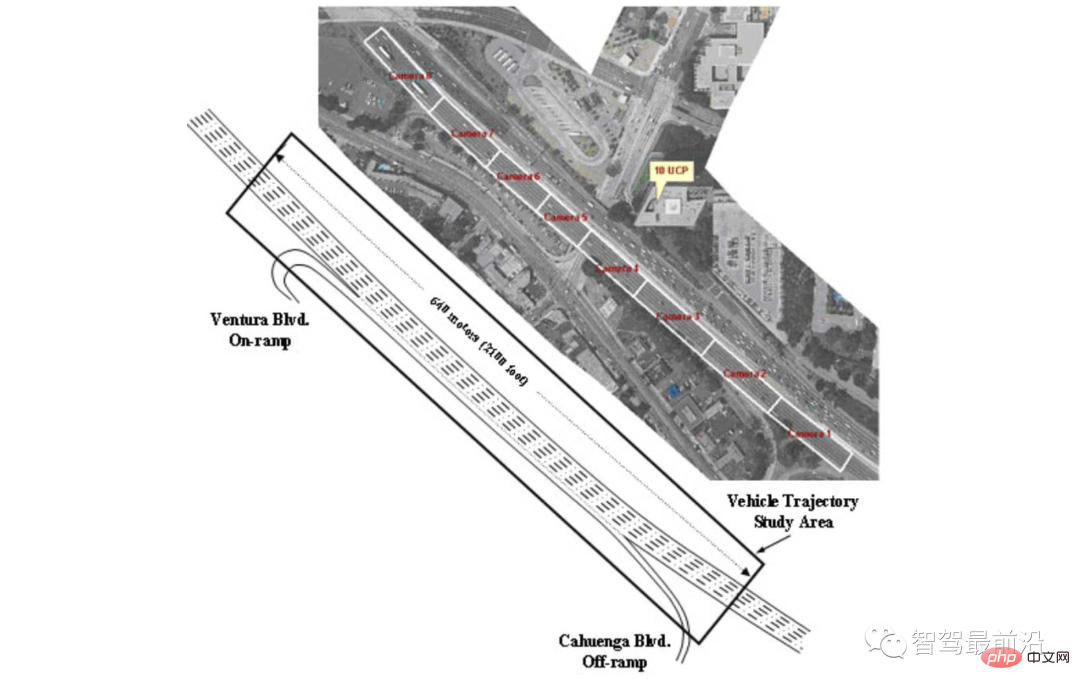
Abbildung 8 Draufsicht auf die Autobahn, die zur Erfassung der US 101-Verkehrsdaten verwendet wird [34]
Dieser Abschnitt umfasst fünf Hauptspuren der Autobahn und eine, die zur Autobahn führt . Auffahrt, eine Ausfahrt zum Verlassen der Autobahn und eine Hilfsspur zum Ein- und Ausfahren auf die Autobahn.
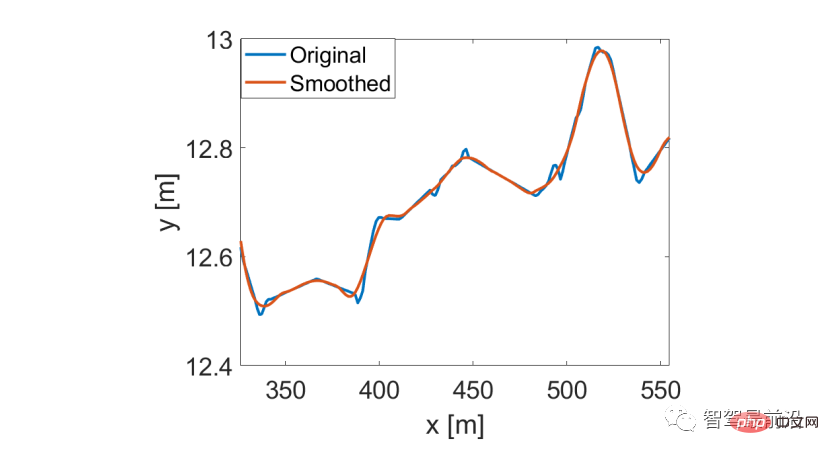
Abbildung 9 Glatte Fahrzeugtrajektorien aus dem US 101-Verkehrsdatensatz unter Verwendung des Savitsky-Gorey-Filters
Für den Validierungstest von LFGC konzentrieren wir uns auf die Auffahrts- und Hilfsspuren Identifizieren Sie alle zusammengeführten Fahrzeuge. Nachdem wir die zusammenfahrenden Fahrzeuge und die entsprechenden Szenarien identifiziert haben, identifizieren wir die interagierenden Fahrzeuge gemäß Abbildung 10. Konkret betrachten wir das erste Fahrzeug auf der Zielspur innerhalb von 2 Sekunden als erstes interagierendes Fahrzeug und die nachfolgenden Fahrzeuge als zweites und drittes Fahrzeug. Alle anderen in der Szene vorhandenen Fahrzeuge werden vom eigenen Fahrzeug als Umgebungsfahrzeuge behandelt und davon ausgegangen, dass sie mit konstanter Geschwindigkeit fahren. Ein identifiziertes Zusammenführungsszenario ist in Abbildung 11 dargestellt.

Abbildung 10 Auswahl interaktiver Fahrzeuge: Das Selbstauto (blaues Fahrzeug) verwendet das Fahrzeug im Auswahlfeld (rotes Feld) als interaktives Fahrzeug
Das vordere Ende des Das Auswahlfeld befindet sich vor dem Self-Car-2-Zeitverlauf. Das erste Fahrzeug auf der Zielspur im Auswahlfeld ist das erste interaktive Fahrzeug, die folgenden Fahrzeuge sind das zweite und dritte interaktive Fahrzeug. Alle anderen Fahrzeuge auf der Autobahn werden als Umgebungsfahrzeuge behandelt und es wird davon ausgegangen, dass sie eine konstante Geschwindigkeit beibehalten.
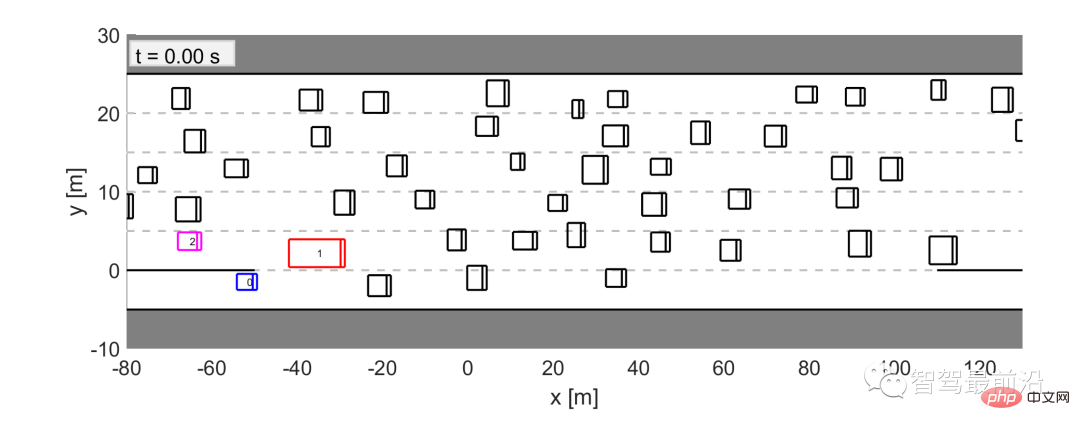
Abbildung 11 Ein zusammengeführtes Szenario, ermittelt aus dem US-101-Verkehrsdatensatz
In diesem Szenario ist Fahrzeug 0 (blaues Fahrzeug) das zusammengeführte Fahrzeug und wir lassen LFGC Fahrzeug 0 steuern. Gemäß unseren Kriterien zur Auswahl interaktiver Fahrzeuge werden Fahrzeug 1 (rotes Fahrzeug) und Fahrzeug 2 (rosa Fahrzeug) als interaktive Fahrzeuge ausgewählt, alle anderen Fahrzeuge (schwarze Fahrzeuge) gelten als Umweltfahrzeuge, vorausgesetzt, sie fahren mit einer festen Geschwindigkeit .
Für jedes zusammengeführte Szenario verwenden wir LFGC, um das Verhalten des eigenen Fahrzeugs und die daraus resultierende Flugbahn zu steuern, anstatt das eigene Fahrzeug Verkehrsdaten verfolgen zu lassen. Alle anderen Fahrzeuge, einschließlich interagierender Fahrzeuge und Umgebungsfahrzeuge, folgen den entsprechenden Trajektorien, wie sie im US 101-Verkehrsdatensatz erscheinen. Das LFGC muss dann die Absichten der interagierenden Fahrzeuge abschätzen und das eigene Fahrzeug so steuern, dass es entsprechend zusammenfährt. Beachten Sie, dass während der Datenerfassung interagierende und umgebende Fahrzeuge während des tatsächlichen Verkehrs mit zusammengeführten Fahrzeugen interagieren können. Da 1) der LFGC möglicherweise anders agiert als der menschliche Betrieb, reagiert das Verhalten des interaktiven Fahrzeugs oder Umgebungsfahrzeugs nicht auf das Verhalten des eigenen Fahrzeugs. Stattdessen ist ihr Verhalten durch den Verkehrsdatensatz vorgegeben, daher müssen konservative Maßnahmen ergriffen werden, um Kollisionen zu vermeiden. 2) Der Verkehr ist dicht und lässt keinen sicheren Spielraum für das Einfädeln eigener Fahrzeuge, ohne die Kollisionszonen anderer Fahrzeuge zu kreuzen.
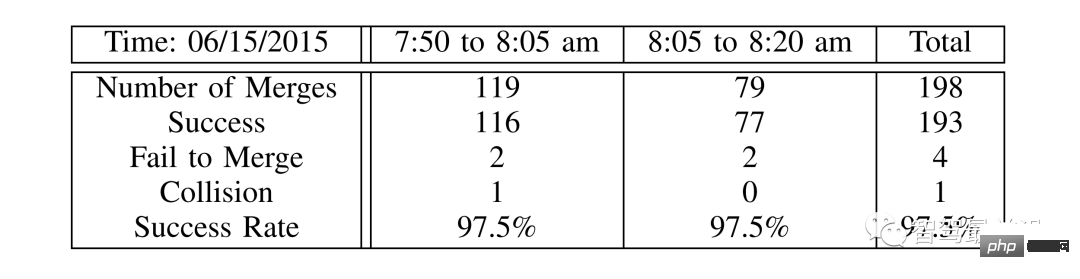
Tabelle 2: Überprüfung der LFGC-Statistiken anhand des US101-Verkehrsdatensatzes
„Erfolgreich“ bedeutet, dass das eigene Fahrzeug ohne Kollision erfolgreich in die Zielspur eingefahren ist. „Einfädeln fehlgeschlagen“ bedeutet, dass das eigene Fahrzeug am Ende der Nebenspur nicht einfädeln kann. Unter „Kollision“ versteht man eine Kollision zwischen dem eigenen Fahrzeug und einem anderen Fahrzeug. Abschließend machte der Autor einen Screenshot des Zusammenführungsprozesses zur Analyse.
In Abbildung 12 zeigen wir einen Screenshot einer erfolgreichen Zusammenführung. In diesen Abbildungen wird das blaue Fahrzeug von LFGC gesteuert, und das graue Kästchen stellt die tatsächliche Position des eigenen Fahrzeugs im Datensatz dar. Alle anderen Fahrzeuge (einschließlich roter interaktiver Fahrzeuge und schwarzer Umweltfahrzeuge) folgen ihren entsprechenden Trajektorien im Datensatz. Das vom LFGC gesteuerte Eigenfahrzeug trifft ähnliche Entscheidungen wie der menschliche Fahrer (graue Box): Sowohl der LFGC als auch der menschliche Fahrer versuchen zunächst, vor dem Lkw (Fahrzeug 1) zu beschleunigen und einzufädeln. Als ihm jedoch klar wurde, dass der Lkw eher weiter nachgeben würde, beschloss er, langsamer zu fahren und hinter dem Lkw einzufädeln. Abbildung 12: Beschreibung der erfolgreichen Zusammenführung bei der Überprüfung von LFGC im US Highway 101-Datensatz Die Daten Die Position des angezeigten Selbstfahrzeugs.
06 Fazit 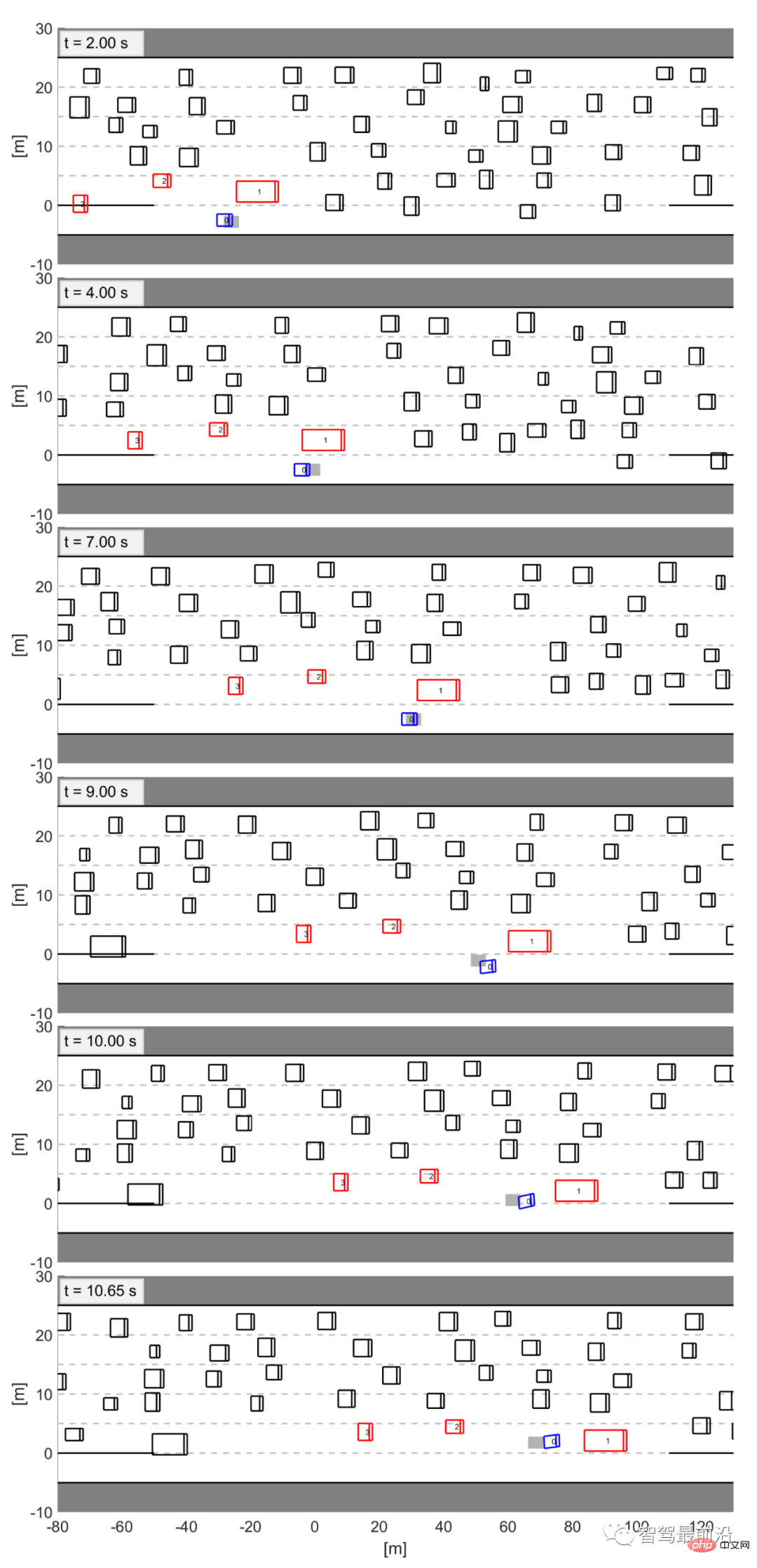
In diesem Dokument haben wir einen Leader-Follower Game Controller (LFGC) für die autonome Fahrzeugplanung und -steuerung in zusammengeführten Szenarien vorgeschlagen. LFGC nimmt die durch unterschiedliche Fahrerabsichten verursachte Interaktionsunsicherheit als latente Variable, schätzt andere Fahrerabsichten und wählt Maßnahmen aus, um das Zusammenführen von Eigenfahrzeugen zu fördern. Insbesondere ist LFGC in der Lage, eine explizite probabilistische Sicherheitseigenschaft zu implementieren, die Fahrzeugsicherheitsbeschränkungen unterliegt.
Durch die Berücksichtigung der paarweisen Interaktion zwischen dem eigenen Fahrzeug und dem interagierenden Fahrzeug ist LFGC in der Lage, Interaktionen mit mehreren Fahrzeugen auf berechenbare Weise abzuwickeln. Schließlich werden mehrere simulationsbasierte Verifizierungen durchgeführt, um die Wirksamkeit von LFGC zu demonstrieren, einschließlich Szenarien, in denen andere Autos dem Spitzenreiter oder Verfolger im Spiel folgen, eines intelligenten Fahrermodells (IDM) und tatsächlicher Daten des US Highway 101.
Dieser Artikel wurde übersetzt aus
„Interaktionsbewusste Trajektorienvorhersage und -planung für autonome Fahrzeuge in Zwangszusammenführungsszenarien“
Das obige ist der detaillierte Inhalt vonFlugbahnvorhersage und -planung für autonomes Fahren unter Zwangsverschmelzung. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Technologietrends, die Sie im Jahr 2023 im Auge behalten sollten
- Wie künstliche Intelligenz Rechenzentrumsteams neue Alltagsaufgaben beschert
- Können künstliche Intelligenz oder Automatisierung das Problem der geringen Energieeffizienz in Gebäuden lösen?
- OpenAI-Mitbegründer im Interview mit Huang Renxun: Die Argumentationsfähigkeiten von GPT-4 haben noch nicht die Erwartungen erfüllt
- Dank der OpenAI-Technologie übertrifft Bing von Microsoft Google im Suchverkehr

