Heim >Technologie-Peripheriegeräte >KI >MIT veröffentlicht erweiterte Version des „Advanced Mathematics'-Lösers: Genauigkeitsrate erreicht 81 % in 7 Kursen
MIT veröffentlicht erweiterte Version des „Advanced Mathematics'-Lösers: Genauigkeitsrate erreicht 81 % in 7 Kursen
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2023-04-12 16:04:101195Durchsuche
KI löst nicht nur Mathe-Textaufgaben in der Grundschule, sondern hat auch damit begonnen, die fortgeschrittene Mathematik zu erobern!
Kürzlich gaben MIT-Forscher bekannt, dass sie auf der Grundlage des OpenAI Codex-Vortrainingsmodells durch Lernen mit wenigen Schüssen erfolgreich eine Genauigkeitsrate von 81 % bei Mathematikproblemen im Grundstudium erreicht haben!

- Papier-Link: https://arxiv.org/abs/2112.15594
- Code-Link: https://github.com/idrori/mathq
Werfen wir einen Blick auf die Antworten auf ein paar kleine Fragen zuerst, wie „Berechnen Sie das Volumen, das durch Drehen des Graphen einer einzelnen variablen Funktion um eine Achse erzeugt wird“, „Berechnen Sie den Lorenz-Attraktor und die Lorenz-Projektion“, „Berechnen und stellen Sie die geometrische Form der Singularwertzerlegung (SVD)“ dar – Sie können sie nicht nur richtig beantworten , aber Sie können auch die entsprechende Erklärung geben!
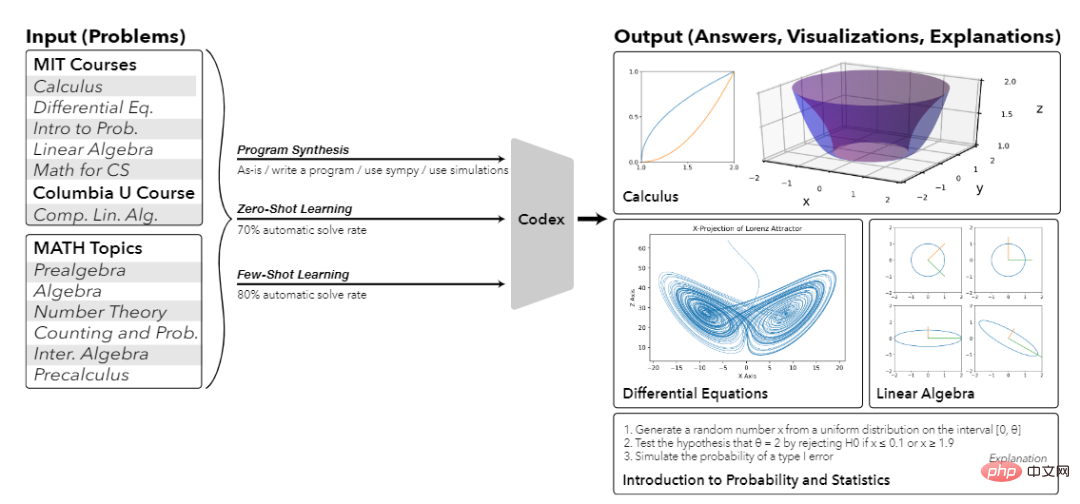
Wenn ich auf die Vergangenheit zurückblicke, kann ich sagen, dass die KI alle 81 Punkte auf einmal erreicht hat.
Was noch erstaunlicher ist, ist, dass diese Forschung nicht nur Probleme löst, die mit gewöhnlichen Modellen des maschinellen Lernens schwer zu lösen sind, sondern auch zeigt, dass diese Technologie in großem Umfang gefördert werden kann und Probleme in ihren Kursen und ähnlichen Kursen lösen kann.
Dies ist auch das erste Mal in der Geschichte, dass ein einzelnes Modell für maschinelles Lernen ein so großes mathematisches Problem lösen und außerdem erklären, zeichnen und sogar neue Fragen generieren kann!
Tatsächlich wurde diese Arbeit bereits zu Beginn des Jahres veröffentlicht. Nach einem halben Jahr der Überarbeitung hat sich der Umfang von 114 Seiten auf 181 Seiten erhöht. Die Anhänge sind von A bis nummeriert Z.

Es gibt vier Hauptautoreneinheiten des Artikels, nämlich MIT, Columbia University, Harvard University und University of Waterloo.
Der Erstautor, Iddo Drori, ist Dozent in der KI-Abteilung des Fachbereichs Elektrotechnik und Informatik am MIT und außerordentlicher Professor an der School of Engineering and Applied Sciences der Columbia University. Gewann den CCAI NeurIPS 2021 Best Paper Award.

Seine Hauptforschungsrichtungen sind maschinelles Lernen für die Bildung, bei dem es darum geht, Maschinen dazu zu bringen, Mathematik auf Hochschulniveau zu lösen, zu erklären und zu generieren, und MINT-Kurse für die Klimawissenschaften, bei denen es darum geht, extreme Klimaveränderungen vorherzusagen und zu überwachen auf Jahrtausende alten Klimadaten, Integration multidisziplinärer Arbeiten zur Vorhersage mehrjähriger Veränderungen in der Ozeanbiogeochemie im Atlantischen Ozean, Algorithmen für maschinelles Lernen usw.
Er ist außerdem Autor von „The Science of Deep Learning“, herausgegeben von Cambridge University Press.
Meilensteine der Hochschulbildung
Vor diesem Artikel glaubten die meisten Forscher, dass neuronale Netze keine Probleme mit hohen Zahlen bewältigen und nur einige einfache mathematische Probleme lösen könnten.
Auch wenn das Transformer-Modell bei verschiedenen NLP-Aufgaben die menschliche Leistung übertrifft, ist es dennoch nicht schlecht bei der Lösung mathematischer Probleme. Der Hauptgrund dafür ist, dass verschiedene große Modelle wie GPT-3 nur auf Textdaten vortrainiert sind.
Später entdeckten einige Forscher, dass das Sprachmodell durch schrittweise Analyse (Gedankenkette) immer noch zum Denken und Beantworten einiger einfacher mathematischer Fragen geführt werden kann, fortgeschrittene mathematische Probleme jedoch nicht so einfach zu lösen sind.

Wenn das Ziel ein Problem mit hoher Anzahl ist, müssen Sie zunächst eine Welle von Trainingsdaten sammeln.
Der Autor hat zufällig 25 Fragen aus jedem der sieben Kurse am MIT ausgewählt, darunter:
- 18.01 Einzelvariablenrechnung
- 18.02 Multivariablenrechnung
- 18.03 Differentialgleichungen
- 18.05 Einführung in Wahrscheinlichkeit und Statistik
- 18.06. Linear Algebra
- 6.042 Informatik Mathematik
- COMS3251 Computational Linear Algebra von der Columbia University
Für den MATH-Datensatz untersuchten die Forscher die Daten aus den sechs Themen des Datensatzes (Algebra, Zählen und Wahrscheinlichkeit, Mittelstufe Algebra, Zahlentheorie, Vor-) 15 zufällig ausgewählte Fragen aus Algebra und Pre-College).
Um zu überprüfen, ob die vom Modell generierten Ergebnisse nicht zu stark an die Trainingsdaten angepasst sind, wählten die Forscher den COMS3251-Kurs, der nicht im Internet veröffentlicht wurde, um die generierten Ergebnisse zu überprüfen.
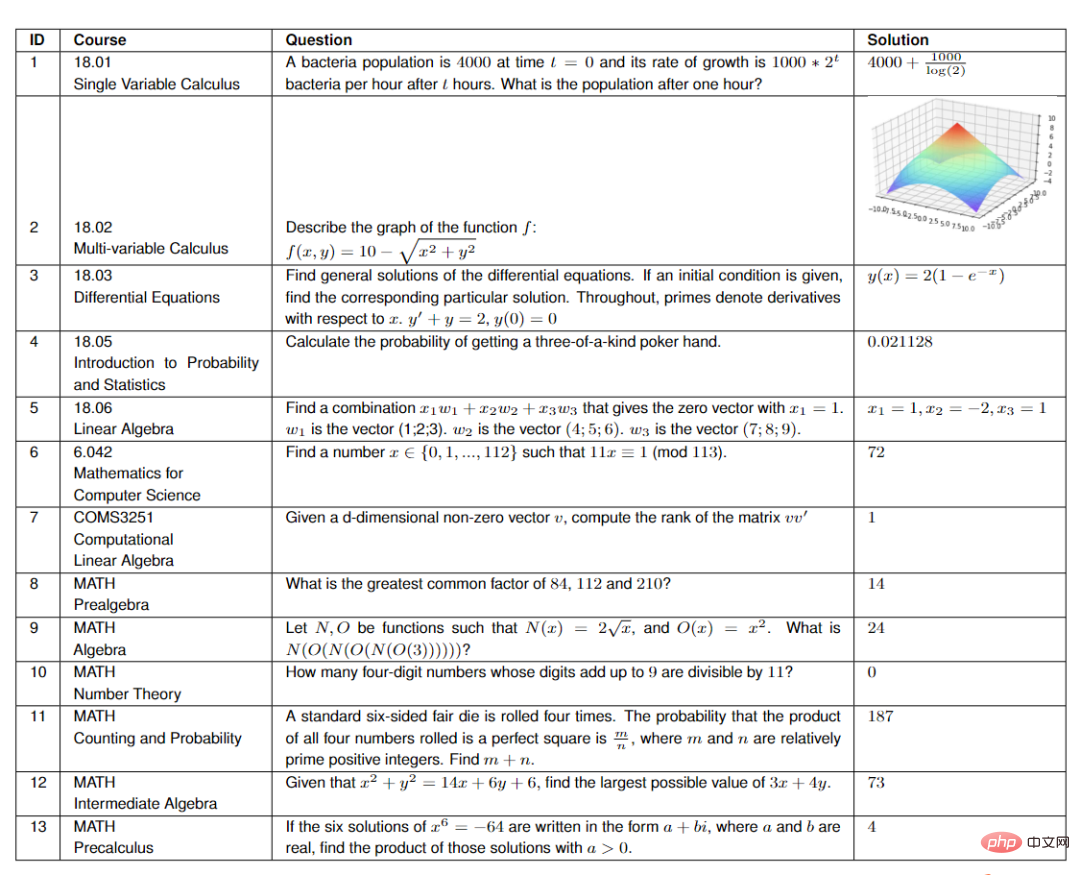
Workflow
Das Modell nimmt eine Kursfrage als Eingabe, führt dann eine automatische Erweiterung mit Kontext durch, führt zu einem synthetisierten Programm und gibt schließlich die Antwort und die generierte Erklärung aus.
Bei verschiedenen Fragen können die Ausgabeergebnisse unterschiedlich sein. Beispielsweise ist die Antwort auf 18.01 eine Gleichung, die Antwort auf 18.02 ein boolescher Wert, die Antworten auf 18.03 und 18.06 ein Diagramm oder ein Vektor und die Antwort auf 18.05 ist ein numerischer Wert.

Wenn Sie eine Frage erhalten, besteht der erste Schritt darin, das Modell den relevanten Kontext der Frage finden zu lassen. Die Forscher konzentrierten sich hauptsächlich auf das von Codex generierte Python-Programm. Daher fügten sie vor der Frage den Text „Programm schreiben“ hinzu und platzierten den Text in drei Anführungszeichen vor dem Python-Programm, um so zu tun, als wäre es ein Dokumentstring im Programm.
Nach dem Generieren des Programms ist eine Codex-Eingabeaufforderung erforderlich, um anzugeben, welche Bibliotheken importiert werden sollen. Der Autor hat sich dafür entschieden, die Zeichenfolge „use sympy“ vor der Frage als Kontext hinzuzufügen und anzugeben, dass das zur Lösung des Problems synthetisierte Programm dieses Paket verwenden soll.
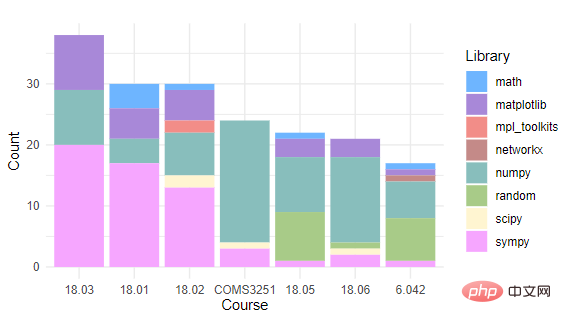
Anhand der Zählung der von jedem Kurs verwendeten Python-Programmierpakete können Sie sehen, dass alle Kurse NumPy und Sympy verwenden. Matplotlib wird nur in Kursen verwendet, bei denen Probleme geplottet werden müssen. Etwa die Hälfte der Kurse verwenden Mathematik, Zufallsprinzipien und SciPy. Während des tatsächlichen Betriebs gaben die Forscher nur SymPy- oder zeichnungsbezogene Pakete für den Import an, während andere importierte Pakete automatisch synthetisiert wurden.
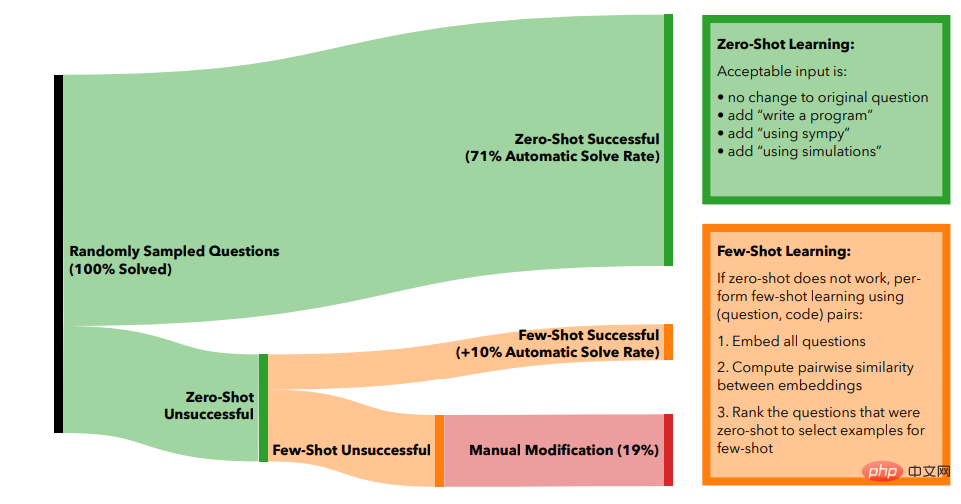
Mit Zero-Shot-Lernen können 71 % der Probleme automatisch gelöst werden, indem nur das ursprüngliche Problem automatisch verbessert wird.
Wenn ein Problem nicht gelöst werden kann, versuchen Forscher, solche Probleme mithilfe von Few-Shot-Learning zu lösen.
Verwenden Sie zunächst die Einbettungs-Engine text-similarity-babbag-001 von OpenAI, um die 2048-dimensionale Einbettung aller Probleme zu erhalten, und verwenden Sie dann Kosinusähnlichkeitsberechnungen für alle Vektoren, um die ungelösten Probleme zu finden, die den gelösten Problemen am ähnlichsten sind. Schließlich werden das ähnlichste Problem und der entsprechende Code als wenige Beispiele für das neue Problem verwendet.
Wenn der generierte Code nicht die richtige Antwort ausgibt, fügen Sie ein weiteres gelöstes Frage-Code-Paar hinzu und verwenden Sie dabei jedes Mal die nächste ähnlich gelöste Frage.
In der Praxis zeigt sich, dass die Verwendung von bis zu 5 Beispielen für das Wenig-Schuss-Lernen die beste Wirkung hat und die Gesamtzahl der Probleme, die automatisch gelöst werden können, von 71 % des Null-Schuss-Lernens auf 81 % des Wenigen-Lernens steigt -Schuss-Lernen.
Um die verbleibenden 19 % der Probleme zu lösen, müssen menschliche Redakteure eingreifen.
Die Forscher sammelten zunächst alle Fragen und stellten fest, dass die meisten dieser Fragen vage waren oder redundante Informationen enthielten, wie etwa Verweise auf Filmfiguren oder aktuelle Ereignisse usw. Die Fragen mussten sortiert werden, um den Kern der Fragen herauszufinden.
Bei der Fragensortierung geht es hauptsächlich darum, überflüssige Informationen zu entfernen, lange Satzstrukturen in kleinere Komponenten zu zerlegen und Eingabeaufforderungen in ein Programmierformat umzuwandeln.
Eine weitere Situation, die manuelles Eingreifen erfordert, besteht darin, dass die Antwort auf eine Frage mehrere Zeichnungsschritte zur Erläuterung erfordert, d. h. der Codex muss interaktiv aufgefordert werden, bis der gewünschte Visualisierungseffekt erreicht ist.
Zusätzlich zur Generierung von Antworten sollte das Modell auch in der Lage sein, die Gründe für die Antworten zu erklären. Die Forscher verwendeten das Eingabeaufforderungswort „Hier ist, was der obige Code tut: 1“, um das Modell bei der Generierung anzuleiten Schritt-für-Schritt-Erklärung der Ergebnisse.
Nachdem Sie die Fragen beantworten können, besteht der nächste Schritt darin, mithilfe von Codex neue Fragen für jeden Kurs zu generieren.
Die Forscher erstellten eine nummerierte Liste mit Fragen, die von den Schülern jeder Klasse verfasst wurden. Diese Liste wurde nach einer zufälligen Anzahl von Fragen abgeschnitten und die Ergebnisse wurden verwendet, um Codex zum Generieren der nächsten Frage zu veranlassen.
Dieser Vorgang wird wiederholt, bis für jeden Kurs genügend neue Fragen erstellt wurden.
Um die generierten Fragen zu bewerten, befragten die Forscher MIT-Studenten, die diese Kurse oder gleichwertige Kurse belegt hatten, um die Qualität und den Schwierigkeitsgrad der maschinell generierten Fragen mit den Originalkursen zu vergleichen.
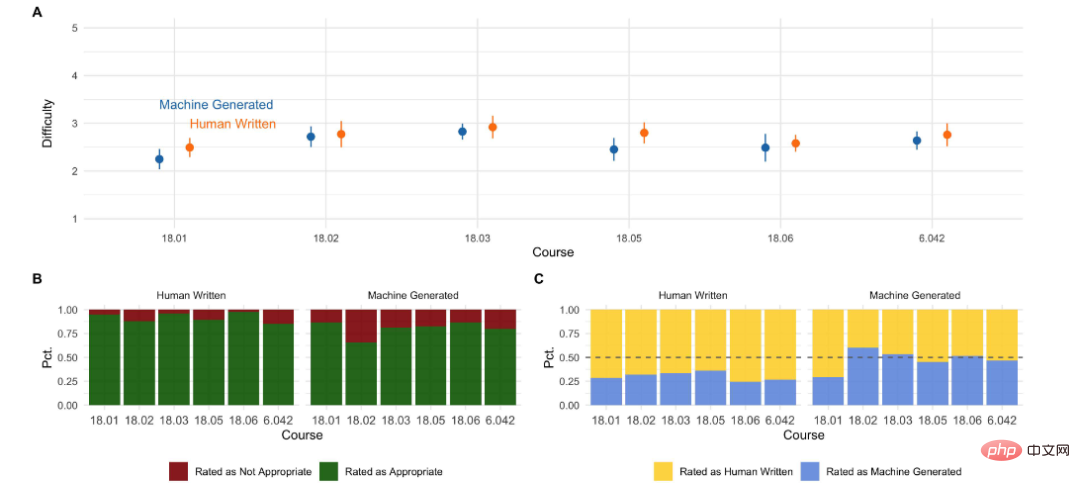
Aus den Ergebnissen der Studierendenbefragung können wir sehen:
- Die Qualität der maschinellen Bewertung ist bereits mit der von menschlichen Fragen vergleichbar.
- Von der Schwierigkeit her eignen sich menschliche Fragen besser als Kursfragen, während maschinell generierte Ergebnisse etwas schwieriger sind.
- Mehr als die Hälfte der Kurse Die Studierenden können sehen, dass die Fragen vom Modell generiert werden. Der 18.01-Kurs kommt dem Menschen am nächsten /
Das obige ist der detaillierte Inhalt vonMIT veröffentlicht erweiterte Version des „Advanced Mathematics'-Lösers: Genauigkeitsrate erreicht 81 % in 7 Kursen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Technologietrends, die Sie im Jahr 2023 im Auge behalten sollten
- Wie künstliche Intelligenz Rechenzentrumsteams neue Alltagsaufgaben beschert
- Können künstliche Intelligenz oder Automatisierung das Problem der geringen Energieeffizienz in Gebäuden lösen?
- OpenAI-Mitbegründer im Interview mit Huang Renxun: Die Argumentationsfähigkeiten von GPT-4 haben noch nicht die Erwartungen erfüllt
- Dank der OpenAI-Technologie übertrifft Bing von Microsoft Google im Suchverkehr

