Heim >Technologie-Peripheriegeräte >KI >rollen! Das Poisson-Strömungserzeugungsmodell des MIT übertrifft das Diffusionsmodell, wenn es um Qualität und Geschwindigkeit geht
rollen! Das Poisson-Strömungserzeugungsmodell des MIT übertrifft das Diffusionsmodell, wenn es um Qualität und Geschwindigkeit geht
- WBOYnach vorne
- 2023-04-12 10:19:051506Durchsuche
Einführung
Das Diffusionsmodell wurde ursprünglich aus der Thermodynamik in der Physik abgeleitet, erfreut sich jedoch in jüngster Zeit auch im Bereich der künstlichen Intelligenz großer Beliebtheit. Welche anderen physikalischen Theorien können die Entwicklung generativer Modellforschung fördern? Kürzlich ließen sich Forscher des MIT von der hochdimensionalen elektromagnetischen Theorie inspirieren und schlugen ein generatives Modell namens Poisson Flow vor. Theoretisch verfügt dieses Modell über intuitive Bilder und eine strenge Theorie; experimentell ist es in Bezug auf Generierungsqualität, Generierungsgeschwindigkeit und Robustheit oft besser als das Diffusionsmodell. Dieser Artikel wurde von NeurIPS 2022 angenommen.

- Papieradresse: https://arxiv.org/abs/2209.11178
- Codeadresse: https://github.com/Newbeeer/Poisson_flow
Inspiriert von der Elektrostatik s, Die Forscher schlugen ein neues generatives Modell namens Poisson-Flow-Modell (Poisson Flow Generative Models oder PFGM) vor. Intuitiv kann diese Forschung die N-dimensionalen Datenpunkte als eine Gruppe positiver Ladungen auf der z=0-Ebene betrachten, einer neuen Dimension im N+1-dimensionalen Raum. Sie erzeugen ein elektrisches Feld im hochdimensionalen Raum. Ausgehend von der z=0-Ebene und entlang der von ihnen erzeugten elektrischen Feldlinien nach außen konnte die Studie die Probe zu einer Halbkugel transportieren (wie in Abbildung 1 dargestellt). Die Richtung dieser elektrischen Feldlinien entspricht dem Gradienten der Lösung der Poisson-Gleichung im hochdimensionalen Raum. Die Forscher bewiesen, dass die elektrischen Feldlinien die Ladungsverteilung (d. h. die Datenverteilung) auf der z=0-Ebene in eine gleichmäßige Verteilung auf der Halbkugel umwandeln können, wenn der Radius der Halbkugel groß genug ist (Abbildung 2).
PFGM nutzt die Reversibilität elektrischer Feldlinien, um eine Datenverteilung auf der z=0-Ebene zu erzeugen: Zuerst nehmen die Forscher gleichmäßig Proben auf einer großen Halbkugel und lassen die Probe dann entlang der elektrischen Feldlinien von der Kugel aus wandern zur z=0-Ebene, wodurch Daten generiert werden. Da die Bewegung entlang elektrischer Feldlinien durch eine gewöhnliche Differentialgleichung (ODE) beschrieben werden kann, müssen Forscher bei der tatsächlichen Probenahme nur eine ODE lösen, die durch die Richtung der elektrischen Feldlinien bestimmt wird. Durch ein elektrisches Feld wandelt PFGM eine einfache Verteilung auf einer Kugel in eine komplexe Datenverteilung um. Aus dieser Perspektive kann PFGM als kontinuierlicher Normalisierungsfluss (Normalisierungsfluss) betrachtet werden.
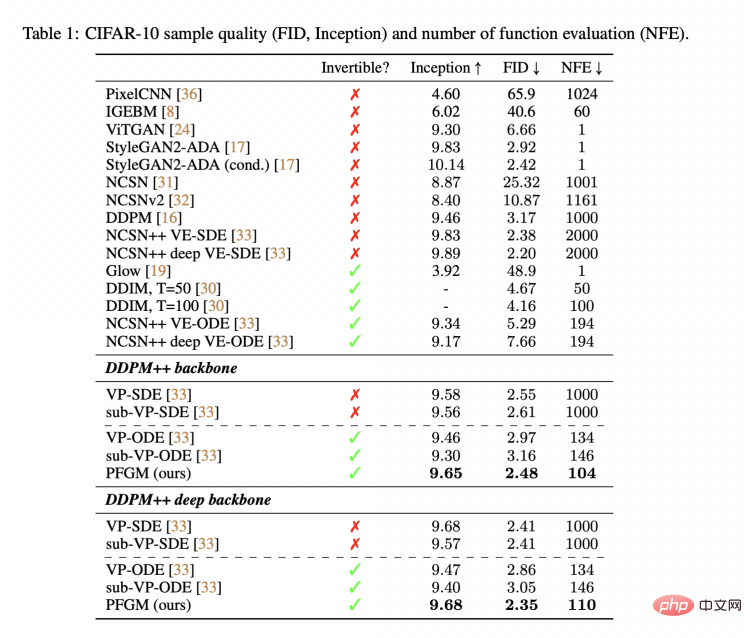
Im Bildgenerierungsexperiment ist PFGM derzeit das leistungsstärkste normalisierte Strömungsmodell auf dem Standarddatensatz CIFAR-10 und erreicht einen FID-Score (ein Maß für die Bildqualität) von 2,35. Die Forscher demonstrierten auch andere Einsatzmöglichkeiten von PFGM, etwa seine Fähigkeit, die Bildwahrscheinlichkeit zu berechnen, Bildbearbeitung durchzuführen und auf hochauflösende Bilddatensätze zu skalieren. Darüber hinaus fanden Forscher heraus, dass PFGM gegenüber den kürzlich populären Diffusionsmodellen drei Vorteile hat:
(1) Bei derselben Netzwerkstruktur ist die vom ODE von PFGM erzeugte Probenqualität viel besser als die ODE des Diffusionsmodells; 2) Während die Erzeugungsqualität der SDE (stochastische Differentialgleichung) des Diffusionsmodells nahezu gleich ist, hat die ODE von PFGM die 10-fache bis 20-fache Beschleunigung erreicht(3) Die Ausdrucksfähigkeit von PFGM ist strukturell höher robuster als Diffusionsmodelle.
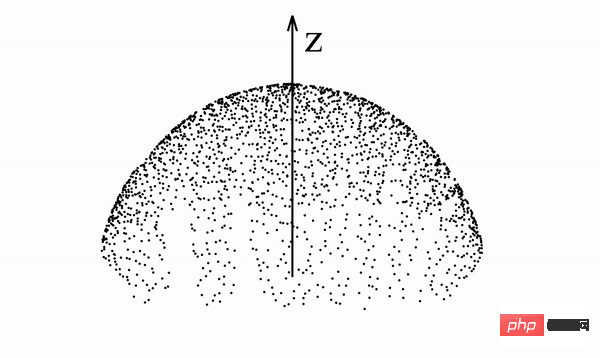
Abbildung 1: Der Probenpunkt bewegt sich entlang der elektrischen Feldlinie. Oben: Die Datenverteilung erfolgt in Form eines Herzens. Unten: Die Daten werden in Form einer PFGM-Vorwärts-ODE und einer Rückwärts-ODE mit PFGM verteilt Beachten Sie, dass der obige Prozess N-dimensionale Daten in den N+1-dimensionalen (zusätzlichen Z-Dimension) Raum einbettet. Um die Unterscheidung zu erleichtern, verwenden Forscher x und wobei Die Trajektorie des elektrischen Feldes Linie (siehe Abbildung 2) kann durch die folgende ODE-Beschreibung berechnet werden: Im folgenden Satz beweisen die Forscher, dass die obige ODE eine Bijektion der gleichmäßigen Verteilung auf der hochdimensionalen Hemisphäre und den Daten definiert Verteilung auf der z=0-Ebene. Diese Schlussfolgerung ist dieselbe wie die Intuition in den Abbildungen 1 und 2: Die Datenverteilung kann durch elektrische Feldlinien wiederhergestellt werden. Training von PFGM Anhand eines aus der Datenverteilung entnommenen Datensatzes Dieser elektrische Feldliniengradient ist das Lernziel. Diese Studie verwendet die perturb-Funktion, um Punkte im Raum auszuwählen, und die Quadratverlustfunktion ermöglicht es dem neuronalen Netzwerk PFGM-Probenahme Nach dem Erlernen der Normalisierung zum Erlernen des normalisierten elektrischen Feldliniengradienten im Raum kann die Datenverteilung über das folgende ODE abgetastet werden: Diese ODE bewirkt, dass sich die Probe allmählich von der großen Kugel entlang der elektrischen Feldlinien zur z=0-Ebene bewegt, indem z reduziert wird. Darüber hinaus schlägt diese Studie vor, die gleichmäßige Verteilung auf einer großen Kugel auf eine bestimmte Z-Ebene zu projizieren, um ODE-Simulationen zu erleichtern und die Probenentnahme durch Variablensubstitution weiter zu beschleunigen. Spezifische Schritte finden Sie in Abschnitt 3.3 des Artikels. In Tabelle 1 verwendet diese Studie den Standarddatensatz CIFAR-10, um verschiedene Modelle zu bewerten. In diesem Datensatz ist PFGM das leistungsstärkste reversible normalisierte Strömungsmodell und erreicht einen FID-Score von 2,35. PFGM bietet eine bessere Leistung als das Diffusionsmodell mit derselben Netzwerkstruktur (DDPM++/DDPM++ tief). Die Forscher stellten außerdem fest, dass die SDE-Generierungsqualität (stochastische Differentialgleichung) des Diffusionsmodells zwar ähnlich war, PFGM jedoch eine 10- bis 20-fache Beschleunigung erreichte, was ein besseres Gleichgewicht zwischen Generierungsqualität und -geschwindigkeit darstellt. Darüber hinaus stellten die Forscher fest, dass PFGM bei Netzwerkstrukturen mit schwächeren Ausdrucksfähigkeiten robuster ist als das Diffusionsmodell und bei höherdimensionalen Datensätzen unter denselben Bedingungen immer noch besser als das Diffusionsmodell. Weitere Informationen finden Sie im experimentellen Abschnitt des Artikels. In Abbildung 3 visualisiert die Studie den Prozess der PFGM-Bilderzeugung. Tabelle 1: Probenqualität (FID, Inception) und Probenschritte (NFE) auf CIFAR-10-Daten Schlussfolgerung Diese Studie schlägt ein generatives PFGM-Modell vor, das auf der Poisson-Gleichung basiert. Dieses Modell sagt normalisierte elektrische Feldliniengradienten in einem erweiterten Raum mit N+1 Dimensionen voraus und wird durch die entsprechenden ODEs der elektrischen Feldlinien abgetastet. In Experimenten ist das in dieser Studie untersuchte Modell derzeit das beste standardisierte Strömungsmodell und erzielte bessere Erzeugungseffekte und eine schnellere Abtastgeschwindigkeit als das Diffusionsmodell auf derselben Netzwerkstruktur. Der Sampling-Prozess von PFGM ist robuster gegenüber Rauschen und kann auch auf höherdimensionale Datensätze erweitert werden. Forscher gehen davon aus, dass PFGM auch in anderen Anwendungsbereichen gute Leistungen erbringen wird, etwa bei der Molekülgenerierung und der 3D-Datengenerierung. Methodenübersicht
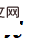 , um N-dimensionale Daten und N+1 Dimensionen darzustellen. Um die oben genannten hochdimensionalen elektrischen Feldlinien zu erhalten, muss die folgende Poisson-Gleichung gelöst werden:
, um N-dimensionale Daten und N+1 Dimensionen darzustellen. Um die oben genannten hochdimensionalen elektrischen Feldlinien zu erhalten, muss die folgende Poisson-Gleichung gelöst werden: 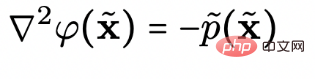
 die Datenverteilung ist, die Sie auf der z=0-Ebene erzeugen möchten;
die Datenverteilung ist, die Sie auf der z=0-Ebene erzeugen möchten;  ist auch die potenzielle Funktion. Dies ist das Ziel, das Forscher lösen wollen. Da nur die Richtung der elektrischen Feldlinie bekannt sein muss, leiteten die Forscher die analytische Form des Gradienten der elektrischen Feldlinie (den Gradienten der Potentialfunktion) ab:
ist auch die potenzielle Funktion. Dies ist das Ziel, das Forscher lösen wollen. Da nur die Richtung der elektrischen Feldlinie bekannt sein muss, leiteten die Forscher die analytische Form des Gradienten der elektrischen Feldlinie (den Gradienten der Potentialfunktion) ab: 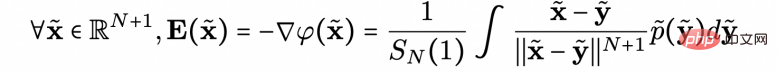


 verwenden die Forscher den dem Datensatz entsprechenden elektrischen Feldliniengradienten, um die entsprechende Datenverteilung anzunähern elektrischer Feldliniengradient:
verwenden die Forscher den dem Datensatz entsprechenden elektrischen Feldliniengradienten, um die entsprechende Datenverteilung anzunähern elektrischer Feldliniengradient: 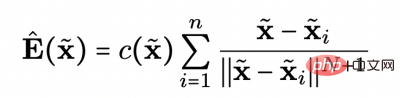
 , den normalisierten elektrischen Feldliniengradienten im Raum zu lernen
, den normalisierten elektrischen Feldliniengradienten im Raum zu lernen  . Der spezifische Algorithmus lautet wie folgt:
. Der spezifische Algorithmus lautet wie folgt: 
Experimentelle Ergebnisse


Das obige ist der detaillierte Inhalt vonrollen! Das Poisson-Strömungserzeugungsmodell des MIT übertrifft das Diffusionsmodell, wenn es um Qualität und Geschwindigkeit geht. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Technologietrends, die Sie im Jahr 2023 im Auge behalten sollten
- Wie künstliche Intelligenz Rechenzentrumsteams neue Alltagsaufgaben beschert
- Können künstliche Intelligenz oder Automatisierung das Problem der geringen Energieeffizienz in Gebäuden lösen?
- OpenAI-Mitbegründer im Interview mit Huang Renxun: Die Argumentationsfähigkeiten von GPT-4 haben noch nicht die Erwartungen erfüllt
- Dank der OpenAI-Technologie übertrifft Bing von Microsoft Google im Suchverkehr

