Stabile Diffusions-Probenahmegeschwindigkeit verdoppelt! Diffusionsmodell-Sampling-Algorithmus in nur 10 bis 25 Schritten

Apropos die einflussreichsten Entwicklungen im Bereich KI in diesem Jahr: Das explosive AI-Mapping ist definitiv eine davon. Designer müssen lediglich eine Textbeschreibung des Bildes eingeben und schon generiert die KI ein hochauflösendes Bild von extrem hoher Qualität. Das derzeit am weitesten verbreitete Modell ist das Open-Source-Modell Stable Diffusion von StabilityAI. Sobald das Modell Open-Source war, sorgte es für breite Diskussionen in der Community.

Das größte Problem bei der Verwendung des Diffusionsmodells ist jedoch seine extrem langsame Abtastgeschwindigkeit. Die Modellabtastung muss mit reinen Rauschbildern beginnen und Schritt für Schritt kontinuierlich entrauschen, um schließlich klare Bilder zu erhalten. Bei diesem Prozess muss das Modell mindestens 50 bis 100 Schritte nacheinander berechnen, um ein Bild mit höherer Qualität zu erhalten. Dies führt dazu, dass die zur Generierung eines Bildes erforderliche Zeit 50 bis 100 Mal so hoch ist wie bei anderen Modellen mit tiefer Generierung, was das Modell stark einschränkt . Bereitstellung und Implementierung.

Um das Sampling von Diffusionsmodellen zu beschleunigen, gehen viele Forscher von der Hardware-Optimierung aus. Beispielsweise verwendet Google die JAX-Sprache, um das Modell zu kompilieren und auszuführen es auf TPU und das OneFlow-Team [1 ] Mithilfe eines selbst entwickelten Compilers erreicht Stable Diffusion eine „Bildausgabe in einer Sekunde“. Diese Methoden basieren auf dem 50-stufigen Sampling-Algorithmus PNDM [2], dessen Sampling-Effekt stark abnimmt, wenn die Anzahl der Schritte reduziert wird.

Vor ein paar Tagen wurde dieser Rekord aktualisiert! Das offizielle Demo[3]-Update von Stable Diffusion zeigt, dass die Zeit zum Abtasten von 8 Bildern direkt von ursprünglich 8 Sekunden auf 4 Sekunden verkürzt wurde! Es ist doppelt so schnell!

Das OneFlow-Team basiert auf der selbst entwickelten Deep-Learning-Compiler-Technologie und reduziert den Sampling-Effekt nicht die bisherige „Bildausgabe in einer Sekunde“ zu „Bildausgabe in einer halben Sekunde“! Erhalten Sie ein hochauflösendes Bild in weniger als 0,5 Sekunden auf der GPU! Verwandte Arbeiten wurden in [1] veröffentlicht.

Tatsächlich kommt die treibende Kraft dieser Arbeiten vom DPM-Solver, der vom TSAIL-Team unter der Leitung von Professor Zhu Jun von der Tsinghua-Universität vorgeschlagen wurde, einem speziellen Modell für Diffusionsmodelle Entwickelter effizienter Löser: Dieser Algorithmus erfordert kein zusätzliches Training, eignet sich sowohl für zeitdiskrete als auch für zeitkontinuierliche Diffusionsmodelle, kann innerhalb von 20 bis 25 Schritten nahezu konvergieren und kann in nur 10 bis eine sehr hochwertige Stichprobe erhalten 15 Schritte. Bei stabiler Diffusion kann ein 25-stufiger DPM-Solver eine bessere Sampling-Qualität erzielen als ein 50-stufiger PNDM, sodass sich die Sampling-Geschwindigkeit direkt verdoppelt!

Projektlink:

• DPM-Solver: Ein schneller ODE-Löser für Diffusionsprobabilistik Modellabtastung in etwa 10 Schritten: https://arxiv.org/abs/2206.00927 (NeurIPS 2022 Oral)
• DPM-Solver++: Schneller Löser für die geführte Abtastung der Diffusion Wahrscheinlichkeitsmodelle: https://arxiv.org/abs/2211.01095
• Open-Source-Projektcode: https://github.com/LuChengTHU/dpm-solver#🎜 🎜 #
• Projekt-Online-Demo: https://huggingface.co/spaces/LuChengTHU/dpmsolver_sdm

Definition von Diffusion Modell Mit der Abtastmethode

wandelt das Diffusionsmodell das Bild schrittweise in Gaußsches Rauschen um, indem es einen Vorwärtsprozess definiert, der kontinuierlich Rauschen hinzufügt, und dann einen Rückwärtsprozess definiert, um das Gaußsche Rauschen schrittweise zu entrauschen Um ein klares Bild zu bekommen:

Während des Probenahmevorgangs kann die Diffusion verändert werden, je nachdem, ob zusätzliches Rauschen vorliegt Die hinzugefügten Modelle sind in zwei Kategorien unterteilt: Eine ist das Diffusions-Stochastische-Differentialgleichungsmodell (Diffusions-SDE) und die andere ist die Diffusions-Gewöhnliche-Differentialgleichung (Diffusions-ODE). Die Trainingszielfunktionen beider Modelle sind die gleichen, sie trainieren ein „Rauschenvorhersagenetzwerk“ durch Minimieren des mittleren quadratischen Fehlers mit Rauschen:

#🎜 🎜 #

Der auf Diffusion SDE basierende Abtastprozess kann als Diskretisierung der folgenden stochastischen Differentialgleichung angesehen werden:

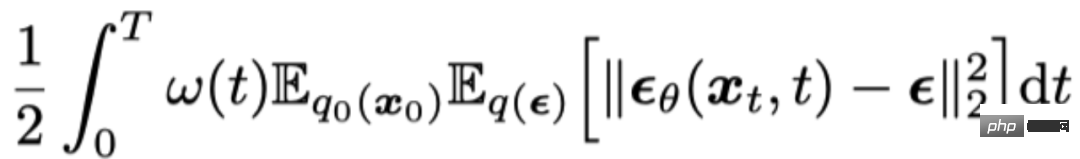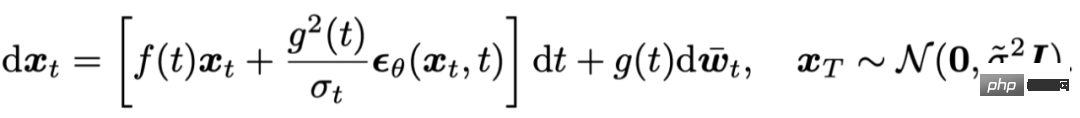#🎜🎜 # Und in [4] wird bewiesen, dass DDPM[5] eine Diskretisierung erster Ordnung der obigen SDE ist.

Der auf der Diffusions-ODE basierende Abtastprozess kann als Diskretisierung der folgenden gewöhnlichen Differentialgleichung angesehen werden:

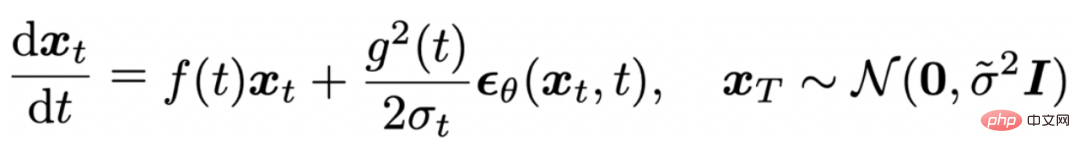
Und es wird in [6] bewiesen, dass DDIM[7] eine Diskretisierung erster Ordnung der obigen ODE ist.

Allerdings konvergieren diese Diskretisierungsmethoden erster Ordnung extrem langsam, und die Abtastung des Diffusionsmodells erfordert normalerweise 100 bis 1000 serielle Berechnungen, um ein qualitativ hochwertiges Bild zu erhalten. Um das Sampling von Diffusionsmodellen zu beschleunigen, verwenden Forscher normalerweise Löser höherer Ordnung für Diffusions-ODE, um den Prozess zu beschleunigen, wie beispielsweise die klassische Runge-Kutta-Methode (RK45). Dies liegt daran, dass ODE keine zusätzliche Zufälligkeit mit sich bringt . Die Diskretisierungsschrittgröße kann relativ größer sein. Nachdem die Lösung zum Zeitpunkt s gegeben ist, basiert die Runge-Kutta-Methode auf der Diskretisierung des folgenden Integrals: ODE und in weniger als 50 Schritten ist es schwierig, zu konvergieren.

DPM-Solver: Ein speziell für Diffusionsmodelle entwickelter Löser

DPM-Solver basiert auf der semilinearen Struktur der Diffusions-ODE. Durch genaue und analytische Berechnung der linearen Terme in der ODE können wir Folgendes erhalten:

Der verbleibende Integralterm ist ein komplexes Integral bezüglich der Zeit. Der Antragsteller von DPM-Solver hat jedoch herausgefunden, dass dieses Integral durch Ändern von log-SNR (logarithmisches Signal-Rausch-Verhältnis) erhalten werden kann, um eine sehr einfache Form zu erhalten:

Das verbleibende Integral ist eine Funktion von Rauschen Exponentiell gewichtetes Integral des Vorhersagemodells. Durch die Taylor-Erweiterung des Rauschvorhersagemodells können wir eine Schätzung des Integrals erhalten:

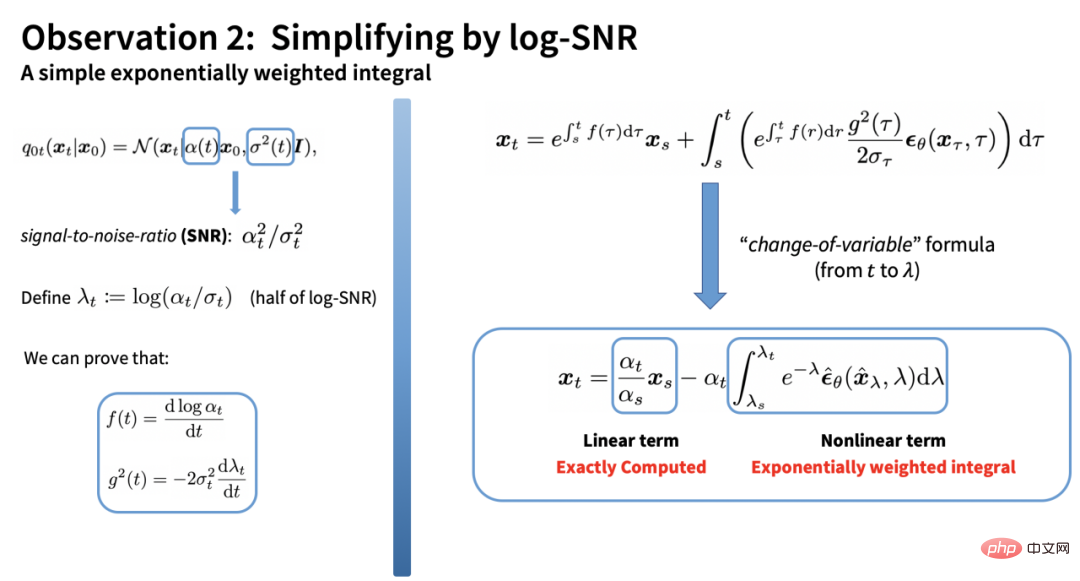
Diese Schätzung enthält zwei Elemente: eines ist der Gesamtableitungsteil (Vektor) und das andere ist der Koeffizient Teil (Skalar). Ein weiterer zentraler Beitrag von DPM-Solver besteht darin, dass der Koeffizient analytisch durch partielle Integration berechnet werden kann:

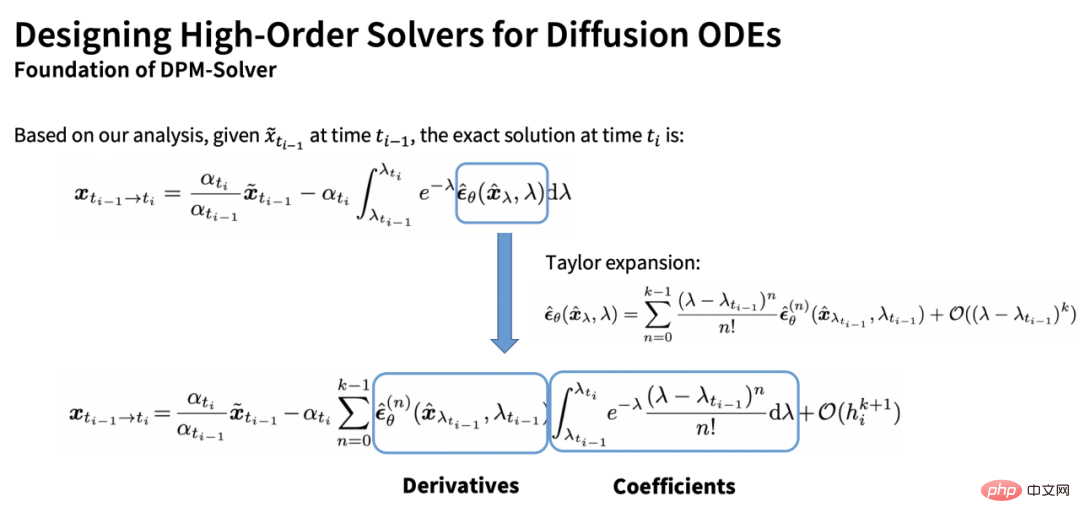
, während der verbleibende gesamte Ableitungsanteil durch numerische Methoden herkömmlicher ODE-Löser (ohne Ableitungsoperation) näherungsweise geschätzt werden kann. :

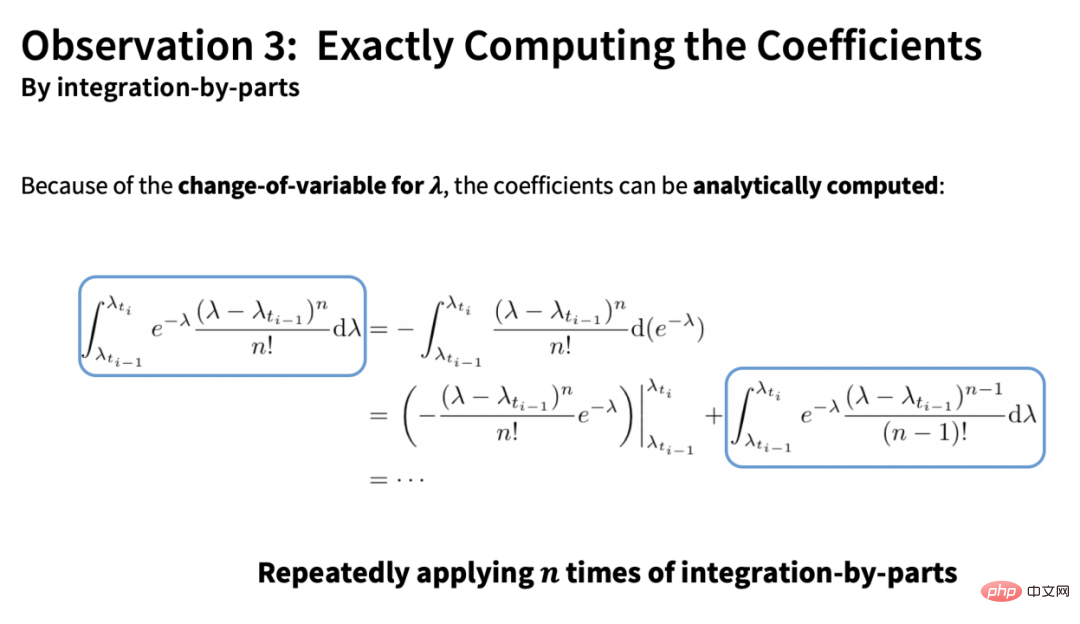
Basierend auf den oben genannten 4 Punkten berechnet DPM-Solver alle bekannten Elemente so genau wie möglich und nähert sich nur dem neuronalen Netzwerkteil an, wodurch der Diskretisierungsfehler minimiert wird:

Außerdem Basierend auf dieser Ableitung können wir feststellen, dass DDIM im Wesentlichen die Form erster Ordnung von DPM-Solver ist, was auch erklären kann, warum DDIM bei geringer Schrittzahl immer noch gute Beschleunigungseffekte erzielen kann:

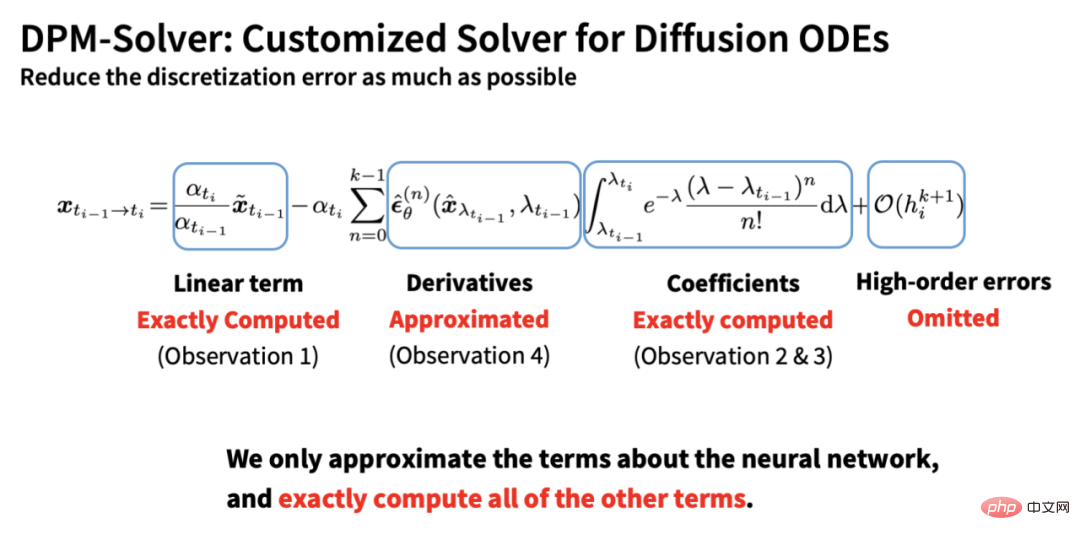
In Im Experiment erzielte DPM-Solver einen Beschleunigungseffekt, der weit über den anderer Sampling-Algorithmen hinausgeht, und er konvergierte nahezu in nur 15–20 Schritten:

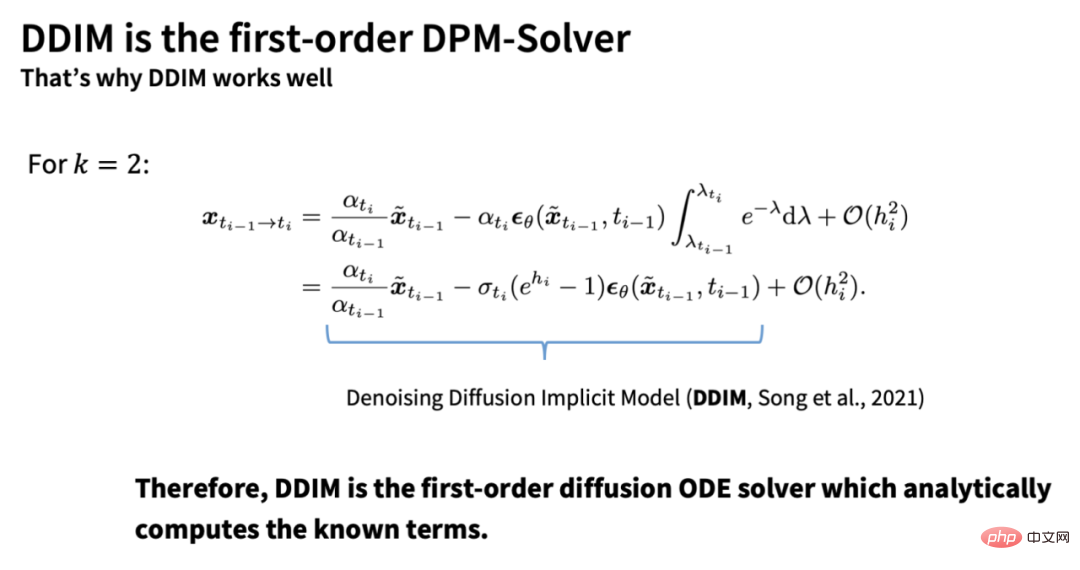
Und die quantitativen Ergebnisse in der Arbeit zeigen, dass der durch DPM-Solver eingeführte zusätzliche Berechnungsaufwand völlig vernachlässigbar ist, d. h. der Beschleunigungseffekt auf die Anzahl der Schritte ist direkt proportional zum Beschleunigungseffekt auf die Zeit - daher basierend auf 25 Mit dem erweiterten DPM-Solver wird die Abtastgeschwindigkeit des Stable-Diffusion-Modells direkt verdoppelt! Die folgende Abbildung zeigt beispielsweise die Auswirkung verschiedener Abtastalgorithmen auf die stabile Diffusion, wenn sich die Anzahl der Schritte ändert. Es ist ersichtlich, dass DPM-Solver in 10 bis 15 Schritten eine Abtastung mit sehr hoher Qualität erzielen kann: # 🎜🎜##🎜 🎜#

Verwendung von DPM-Solver

Die Verwendung von DPM-Solver ist sehr einfach, man kann darauf aufbauen den offiziellen Code des Autors, oder Sie können die Mainstream Diffusers-Bibliothek verwenden. Basierend auf dem offiziellen Code des Autors (https://github.com/LuChengTHU/dpm-solver) sind beispielsweise nur 3 Zeilen erforderlich:

# 🎜🎜#Der offizielle Code unterstützt 4 Diffusionsmodelle:

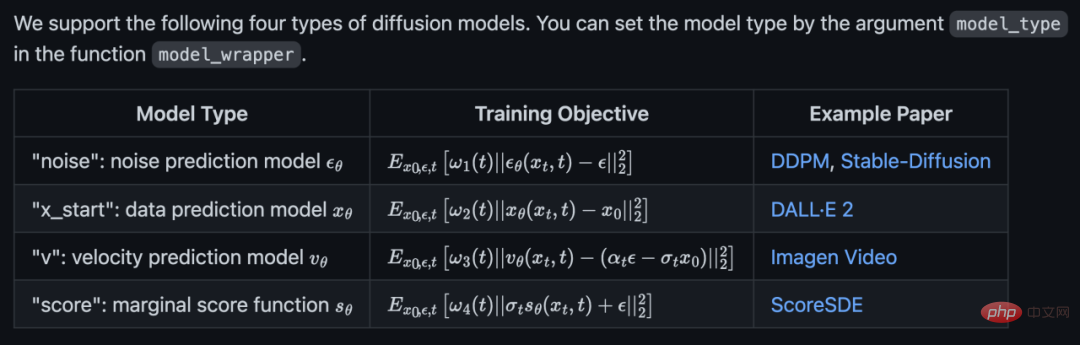und unterstützt sie gleichzeitig bedingungslose Probenahme, Klassifikatorführung und klassifikatorfreie Führung:

Der DPM-Solver basiert auf Auch die Diffusers-Bibliothek ist sehr einfach, man muss nur den Scheduler definieren:

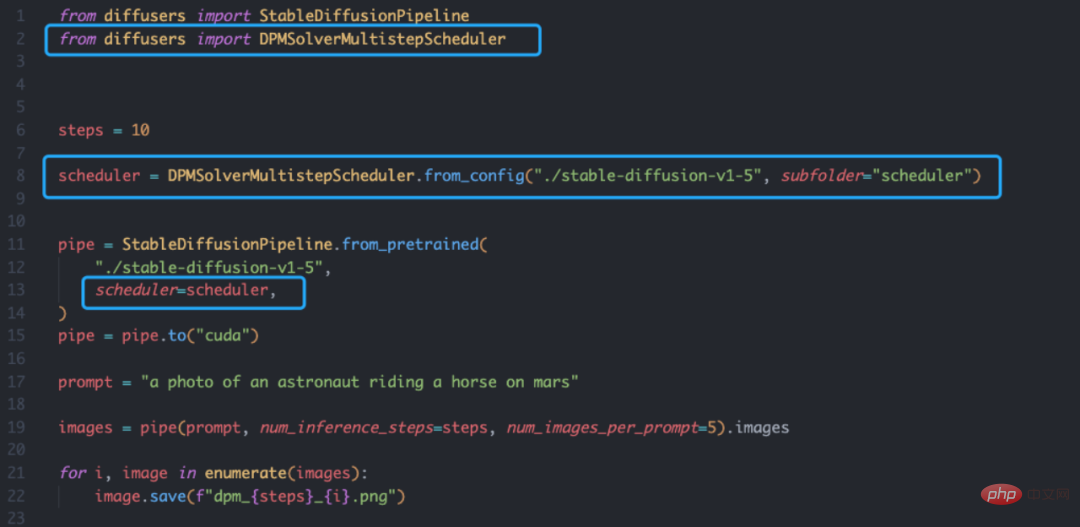Außerdem das Autorenteam Bietet auch eine Online-Demo: https://huggingface.co/spaces/LuChengTHU/dpmsolver_sdm

Das Bild unten ist ein Beispiel für 15 Schritte Die Bildqualität ist bereits sehr hoch:

#🎜🎜 #

Ich glaube, dass basierend auf DPM-Solver die Abtastgeschwindigkeit der Diffusion Modell wird kein Engpass mehr sein.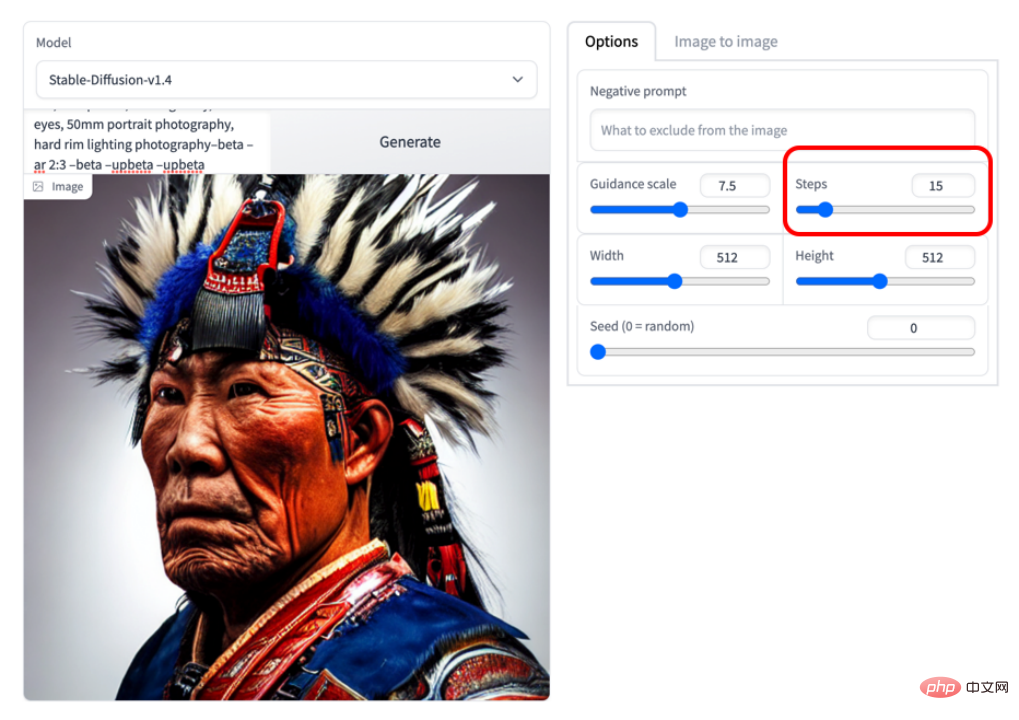

Über den Autor

DPM-Solver Der Erstautor des Artikels ist Dr. Lu Cheng vom TSAIL-Team der Tsinghua-Universität schreibt über das Diffusionsmodell auf Zhihu. Ich habe in der Diskussion, die derzeit über 2000 Likes hat, auch eine einführende Einführung in die Prinzipien des Diffusionsmodells geschrieben: https://www.zhihu.com/question/536012286/answer/2533146567#🎜 🎜#

#🎜 🎜#

Das TSAIL-Team der Tsinghua-Universität widmet sich seit langem der Theorie und Algorithmenforschung des Bayes'schen maschinellen Lernens Es wurden in Bayes'schen Modellen effiziente Algorithmen und probabilistische Programmierbibliotheken entwickelt. Ein weiterer Doktorand im Team, Bao Fan, schlug Analytic-DPM [8][9] vor, das eine einfache und überraschende analytische Form für den optimalen Mittelwert und die optimale Varianz des Diffusionsmodells lieferte, und gewann den ICLR 2022 Outstanding Paper Award. In Bezug auf die probabilistische Programmierung berichtete Machine Heart über die vom Team bereits 2017 veröffentlichte Deep Probabilistic Programming-Bibliothek „ZhuSuan“ (https://zhusuan.readthedocs.io/en/latest/) [10], was die früheste ist in der Welt. Eine der Programmierbibliotheken für tiefe Wahrscheinlichkeitsmodelle. Darüber hinaus ist es erwähnenswert, dass die beiden Hauptautoren des Diffusionswahrscheinlichkeitsmodells, Song Yang und Song Jiaming, beide als Studenten eine wissenschaftliche Forschungsausbildung unter der Leitung von Professor Zhu Jun erhielten und später an der Stanford University promovierten . Die Co-Autoren des Artikels, Zhou Yuhao, Chen Jianfei und Li Chongxuan, sind ebenfalls herausragende Doktoranden, die von der TSAIL-Gruppe ausgebildet wurden, und Chen Jianfei und Li Chongxuan lehren am Institut für Informatik in Tsinghua University bzw. der Hillhouse School of Artificial Intelligence der Renmin University.

Das obige ist der detaillierte Inhalt vonStabile Diffusions-Probenahmegeschwindigkeit verdoppelt! Diffusionsmodell-Sampling-Algorithmus in nur 10 bis 25 Schritten. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!