Unglaublich! Verwenden Sie Numpy, um ein Deep-Learning-Framework zu entwickeln und den Trainingsprozess für neuronale Netze zu untersuchen

Hallo zusammen.

Heute möchte ich ein sehr tolles Open-Source-Projekt mit Ihnen teilen. Ich habe mit Numpy ein Deep-Learning-Framework entwickelt. Die Syntax ist im Grunde die gleiche wie bei Pytorch.

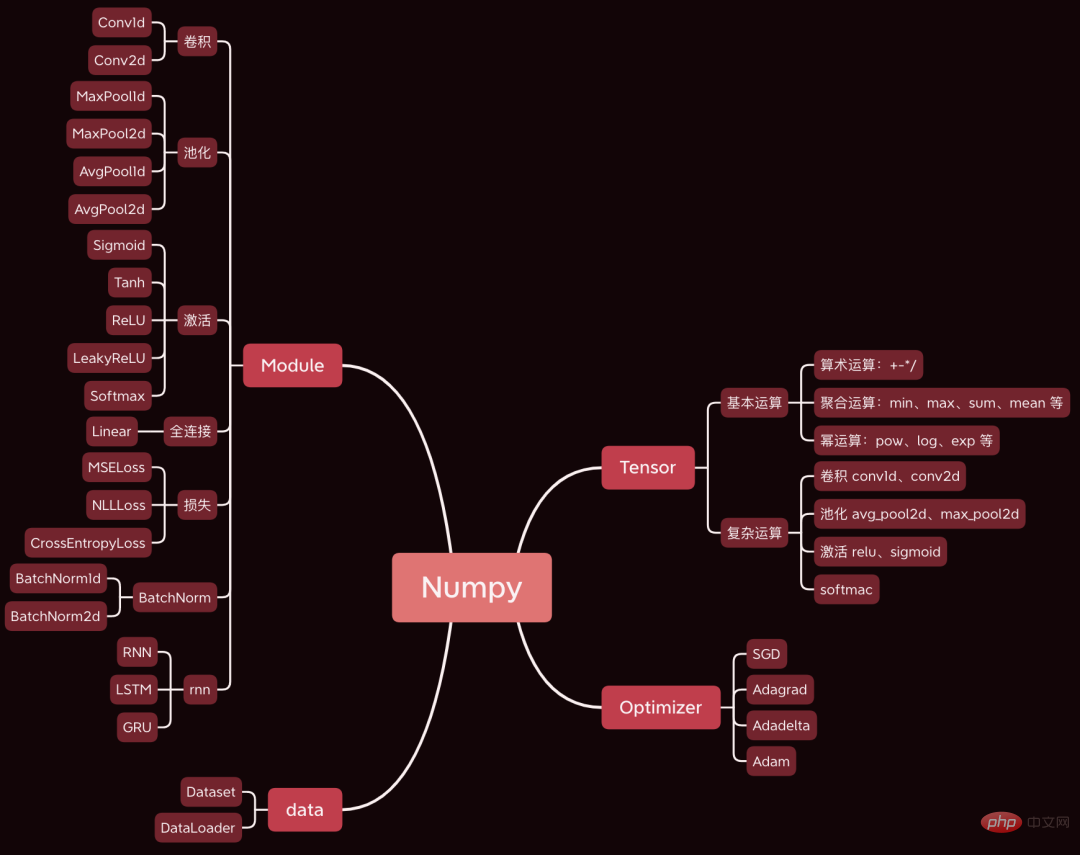
Heute nehmen wir ein einfaches Faltungs-Neuronales Netzwerk als Beispiel, um den Quellcode der Kernschritte des Trainingsprozesses des Neuronalen Netzwerks zu analysieren, wie z. B. Vorwärtsausbreitung, Rückausbreitung und Parameteroptimierung.

Die verwendeten Datensätze und Codes wurden gepackt. Am Ende des Artikels finden Sie Möglichkeiten, sie abzurufen.

1. Vorbereitung

Bereiten Sie zunächst die Daten und den Code vor.

1.1 Erstellen Sie das Netzwerk

Laden Sie zunächst den Quellcode des Frameworks herunter unter: https://github.com/duma-repo/PyDyNet

git clone https://github.com/duma-repo/PyDyNet.git

Erstellen Sie das LeNet-Faltungs-Neuronale Netzwerk und trainieren Sie das Drei-Klassifizierungs-Modell.

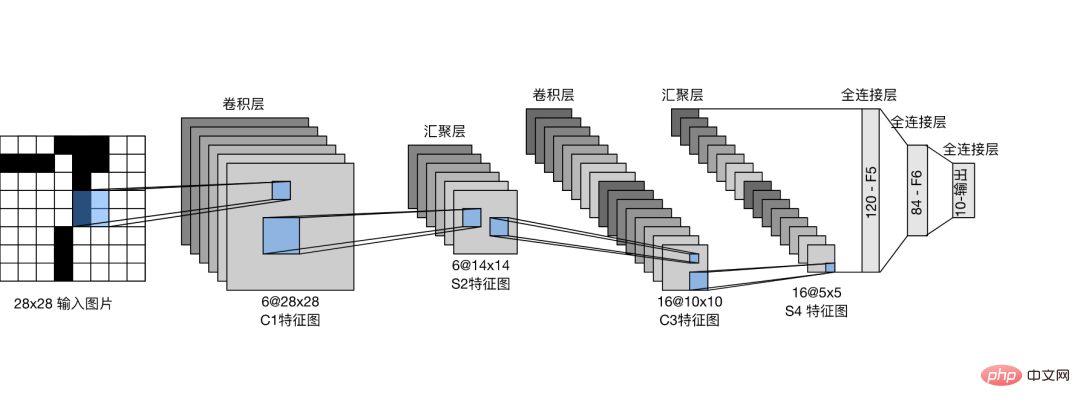
Erstellen Sie die Codedatei direkt im PyDyNet-Verzeichnis.

from pydynet import nn

class LeNet(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 6, kernel_size=5, padding=2)
self.conv2 = nn.Conv2d(6, 16, kernel_size=5)
self.avg_pool = nn.AvgPool2d(kernel_size=2, stride=2, padding=0)
self.sigmoid = nn.Sigmoid()
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 3)

def forward(self, x):
x = self.conv1(x)
x = self.sigmoid(x)
x = self.avg_pool(x)

x = self.conv2(x)
x = self.sigmoid(x)
x = self.avg_pool(x)

x = x.reshape(x.shape[0], -1)

x = self.fc1(x)
x = self.sigmoid(x)
x = self.fc2(x)
x = self.sigmoid(x)
x = self.fc3(x)

return x

Sie können sehen, dass die Definition des Netzwerks genau mit der Pytorch-Syntax übereinstimmt.

In dem von mir bereitgestellten Quellcode wird die Zusammenfassungsfunktion zum Drucken der Netzwerkstruktur bereitgestellt.

1.2 Daten vorbereiten

Die Trainingsdaten verwenden den Fanshion-MNIST-Datensatz, der 10 Bildkategorien, 6.000 Bilder in jeder Kategorie, enthält.

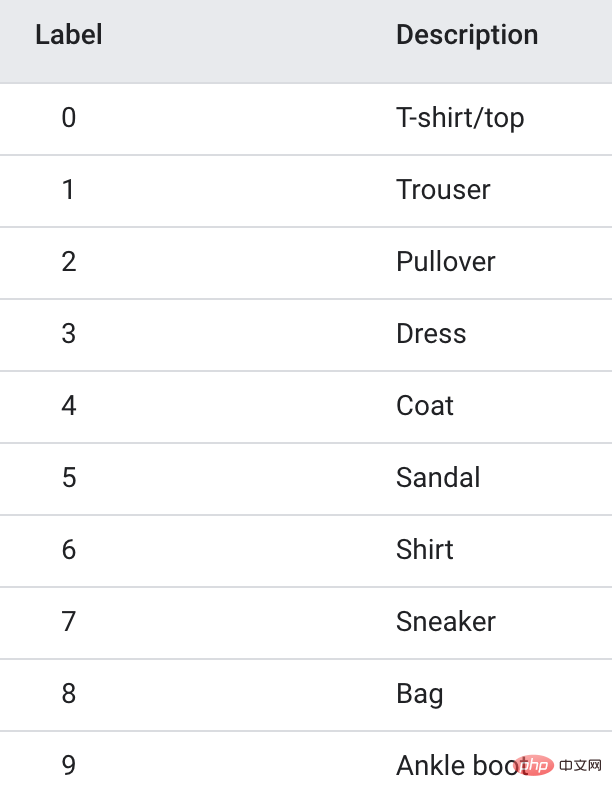
Um das Training zu beschleunigen, habe ich nur die ersten drei Kategorien, insgesamt 1,8 W-Trainingsbilder, extrahiert, um ein Modell mit drei Klassifizierungen zu erstellen.

1.3 Modelltraining

import pydynet
from pydynet import nn
from pydynet import optim

lr, num_epochs = 0.9, 10
optimizer = optim.SGD(net.parameters(),
lr=lr)
loss = nn.CrossEntropyLoss()

for epoch in range(num_epochs):
net.train()
for i, (X, y) in enumerate(train_iter):
optimizer.zero_grad()
y_hat = net(X)
l = loss(y_hat, y)
l.backward()
optimizer.step()

with pydynet.no_grad():
metric.add(l.numpy() * X.shape[0],
 accuracy(y_hat, y),
 X.shape[0])

Der Trainingscode ist auch der gleiche wie bei Pytorch.

Der wichtigste Schritt besteht darin, sich mit dem Quellcode des Modelltrainings zu befassen, um die Prinzipien des Modelltrainings zu erlernen.

2. train, no_grad und eval

net.train werden aufgerufen, bevor das Modell mit dem Training beginnt.

def train(self, mode: bool = True):
set_grad_enabled(mode)
self.set_module_state(mode)

Sie können sehen, dass grad​(Gradient) auf True​ gesetzt wird und der anschließend erstellte Tensor einen Gradienten haben kann. Nachdem Tensor den Gradienten gebracht hat, wird er in das Berechnungsdiagramm eingefügt und wartet auf die Ableitung, um den Gradienten zu berechnen.

Das Folgende mit no_grad(): Code

class no_grad:
def __enter__(self) -> None:
self.prev = is_grad_enable()
set_grad_enabled(False)

setzt grad​(Gradient) auf False​, sodass der später erstellte Tensor nicht in das Berechnungsdiagramm eingefügt wird und es natürlich nicht erforderlich ist, den Gradienten zu berechnen. was die Schlussfolgerung beschleunigen kann.

Wir sehen häufig die Verwendung von net.eval() in Pytorch und werfen auch einen Blick auf den Quellcode.

def eval(self):
return self.train(False)

Sie können sehen, dass train(False)​ direkt aufgerufen wird, um den Farbverlauf auszuschalten, und der Effekt ist ähnlich wie bei no_grad().

Also generell vor dem Training den Zug anrufen, um das Gefälle einzuschalten. Rufen Sie nach dem Training eval auf, um den Gradienten zu schließen und eine schnelle Schlussfolgerung zu ermöglichen.

3. Vorwärtsausbreitung

Neben der Berechnung der Kategoriewahrscheinlichkeit besteht das Wichtigste bei der Vorwärtsausbreitung darin, die Tensoren im Netzwerk in der Reihenfolge der Vorwärtsausbreitung zu organisieren Rückausbreitung. Der Gradient des Tensors.

Tensor in neuronalen Netzen wird nicht nur zum Speichern von Daten verwendet, sondern auch zum Berechnen und Speichern von Gradienten.

Nehmen Sie die Faltungsoperation der ersten Ebene als Beispiel, um zu sehen, wie ein Berechnungsdiagramm erstellt wird.

def conv2d(x: tensor.Tensor,
 kernel: tensor.Tensor,
 padding: int = 0,
 stride: int = 1):
'''二维卷积函数
'''
N, _, _, _ = x.shape
out_channels, _, kernel_size, _ = kernel.shape
pad_x = __pad2d(x, padding)
col = __im2col2d(pad_x, kernel_size, stride)
out_h, out_w = col.shape[-2:]
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N * out_h * out_w, -1)
col_filter = kernel.reshape(out_channels, -1).T
out = col @ col_filter
return out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)

x​ ist das Eingabebild und muss den Farbverlauf nicht aufzeichnen. Der Kernel ist das Gewicht des Faltungskerns und muss den Gradienten berechnen.

Der durch pad_x = __pad2d(x, padding)​ generierte neue Tensor hat also auch keinen Gradienten und muss daher nicht zum Berechnungsdiagramm hinzugefügt werden.

Der von kernel.reshape(out_channels, -1) erzeugte Tensor muss den Gradienten berechnen und auch zum Berechnungsdiagramm hinzugefügt werden.

Werfen wir einen Blick auf den Zusammenführungsprozess:

def reshape(self, *new_shape):
return reshape(self, new_shape)

class reshape(UnaryOperator):
'''
张量形状变换算子，在Tensor中进行重载

Parameters
----------
new_shape : tuple
变换后的形状，用法同NumPy
'''
def __init__(self, x: Tensor, new_shape: tuple) -> None:
self.new_shape = new_shape
super().__init__(x)

def forward(self, x: Tensor)
return x.data.reshape(self.new_shape)

def grad_fn(self, x: Tensor, grad: np.ndarray)
return grad.reshape(x.shape)

Die Reshape-Funktion gibt ein Reshape-Klassenobjekt zurück. Die Reshape-Klasse erbt die UnaryOperator-Klasse und in der Funktion __init__ wird die Initialisierungsfunktion der übergeordneten Klasse aufgerufen. Die

class UnaryOperator(Tensor):
def __init__(self, x: Tensor) -> None:
if not isinstance(x, Tensor):
x = Tensor(x)
self.device = x.device
super().__init__(
data=self.forward(x),
device=x.device,
# 这里 requires_grad 为 True
requires_grad=is_grad_enable() and x.requires_grad,
)

UnaryOperator-Klasse erbt die Tensor-Klasse, daher ist das Reshape-Objekt auch ein Tensor.

In der Funktion __init__​ von UnaryOperator wird die Initialisierungsfunktion von Tensor aufgerufen. Der übergebene Parameter „required_grad“ ist „True“, was bedeutet, dass der Gradient berechnet werden muss. Der Berechnungscode von

requires_grad​ ist is_grad_enable() und x.requires_grad is_grad_enable()​ wurde vom Zug auf True gesetzt, und x​ ist der Faltungskern, und sein require_grad​ ist ebenfalls True.

class Tensor:
def __init__(
self,
data: Any,
dtype=None,
device: Union[Device, int, str, None] = None,
requires_grad: bool = False,
) -> None:
if self.requires_grad:
# 不需要求梯度的节点不出现在动态计算图中
Graph.add_node(self)

Rufen Sie schließlich in der Initialisierungsmethode der Tensor-Klasse Graph.add_node(self) auf, um den aktuellen Tensor zum Berechnungsdiagramm hinzuzufügen.

In ähnlicher Weise werden die neuen Tensoren, die unten häufig zu sehen sind und den Tensor verwenden, der „requires_grad=True“ erfordert, in das Berechnungsdiagramm eingefügt.

Nach einer Faltungsoperation werden dem Berechnungsdiagramm 6 Knoten hinzugefügt.

4. Backpropagation

Nachdem eine Vorwärtspropagation abgeschlossen ist, beginnen Sie beim letzten Knoten im Berechnungsdiagramm und führen Sie die Backpropagation von hinten nach vorne durch.

l = loss(y_hat, y)
l.backward()

breitet sich Schicht für Schicht durch das Vorwärtsnetzwerk aus und erreicht schließlich den Verlusttensor l.

Ausgehend von l als Ausgangspunkt und Ausbreitung von vorne nach hinten kann der Gradient jedes Knotens im Berechnungsdiagramm berechnet werden.

Der Kerncode von Backward lautet wie folgt:

def backward(self, retain_graph: bool = False):

for node in Graph.node_list[y_id::-1]:
grad = node.grad
for last in [l for l in node.last if l.requires_grad]:
add_grad = node.grad_fn(last, grad)

last.grad += add_grad

Graph.node_list[y_id::-1] sortiert das Berechnungsdiagramm in umgekehrter Reihenfolge.

node​是前向传播时放入计算图​中的每个tensor。

node.last​ 是生成当前tensor的直接父节点。

调用node.grad_fn计算梯度，并反向传给它的父节点。

grad_fn​其实就是Tensor的求导公式，如：

class pow(BinaryOperator):
'''
幂运算算子，在Tensor类中进行重载

See also
--------
add : 加法算子
'''
def grad_fn(self, node: Tensor, grad: np.ndarray)
if node is self.last[0]:
return (self.data * self.last[1].data / node.data) * grad

return​后的代码其实就是幂函数求导公式。

假设y=x^2，x​的导数为2x。

5. 更新参数

反向传播计算梯度后，便可以调用优化器，更新模型参数。

l.backward()
optimizer.step()

本次训练我们用梯度下降SGD算法优化参数，更新过程如下：

def step(self):
for i in range(len(self.params)):
grad = self.params[i].grad + self.weight_decay * self.params[i].data
self.v[i] *= self.momentum
self.v[i] += self.lr * grad
self.params[i].data -= self.v[i]
if self.nesterov:
self.params[i].data -= self.lr * grad

self.params​是整个网络的权重，初始化SGD时传进去的。

step​函数最核心的两行代码，self.v[i] += self.lr * grad​ 和 self.params[i].data -= self.v[i]​，用当前参数 - 学习速率 * 梯度​更新当前参数。

这是机器学习的基础内容了，我们应该很熟悉了。

一次模型训练的完整过程大致就串完了，大家可以设置打印语句，或者通过DEBUG的方式跟踪每一行代码的执行过程，这样可以更了解模型的训练过程。

Das obige ist der detaillierte Inhalt vonUnglaublich! Verwenden Sie Numpy, um ein Deep-Learning-Framework zu entwickeln und den Trainingsprozess für neuronale Netze zu untersuchen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!