Heim >Technologie-Peripheriegeräte >KI >Zusammenfassung der wichtigsten technischen Ideen und Methoden der kausalen Schlussfolgerung
Zusammenfassung der wichtigsten technischen Ideen und Methoden der kausalen Schlussfolgerung
- WBOYnach vorne
- 2023-04-12 08:10:052433Durchsuche

Einleitung: Kausale Schlussfolgerung ist ein wichtiger Zweig der Datenwissenschaft. Sie spielt eine wichtige Rolle bei der Produktiteration, Algorithmen- und Anreizstrategiebewertung im Internet und in Industriekreisen. Sie wird mit Daten, Experimenten oder statistischen ökonometrischen Modellen kombiniert Die Berechnung des Nutzens neuer Veränderungen ist die Grundlage für die Entscheidungsfindung. Der Kausalschluss ist jedoch keine einfache Angelegenheit. Erstens verwechseln Menschen im täglichen Leben oft Korrelation und Kausalität. Korrelation bedeutet oft, dass zwei Variablen die Tendenz haben, gleichzeitig zuzunehmen oder zu sinken, aber Kausalität bedeutet, dass wir wissen wollen, was passiert, wenn wir eine Variable ändern, oder dass wir ein kontrafaktisches Ergebnis erwarten, wenn wir es in der Zeit getan haben Vergangenheit Wenn wir unterschiedliche Maßnahmen ergreifen, wird es in Zukunft Veränderungen geben? Die Schwierigkeit besteht jedoch darin, dass kontrafaktische Daten in der realen Welt oft nur schwer zu beobachten und zu sammeln sind.
Dieser Artikelbespricht die wichtigsten technischen Ideen und Methoden der beiden Schulen der Kausalinferenz – das Rubin-Kausalmodell (RCM; Rubin 1978) und das Kausaldiagramm (Pearl 1995) sowie die jüngsten Entwicklungen in Neue Methoden und Anwendungen. Da der akademische Hintergrund des Autors relativ mit der Ökonometrie verwandt ist, beziehen sich die zitierten Methoden und Arbeiten hauptsächlich auf die Wirtschaftsliteratur. Es kann zu einigen Auslassungen in der Tiefe und Breite der Theorie und Anwendung einiger Methoden kommen.
Potenzielles Ergebnismodell
Wir verwenden i, um jedes Forschungsobjekt oder jeden Benutzer darzustellen, der bestimmte strategische Interventionen erhalten kann: Ti=1stellt die Intervention dar (Versuchsgruppe), Ti=0 stellt keine Intervention dar ( Basisgruppe) und die entsprechenden Ergebnisse, die uns wichtig sind, sind Yi0 bzw. Yi1, aber nur eine Situation wird tatsächlich eintreten, nämlich Yi0 und Yi1 nur einer von ihnen kann beobachtet werden, der andere ist unbekannt. Das kausale Schlussfolgerungsergebnis, das wir hier erwarten, ist der durchschnittliche Behandlungseffekt ATE=E[Y1-Y0].
Wir können die Schwierigkeit der Schätzung des ATE durch bestimmte mathematische Ableitungen erklären. Da wir nur eines von Yi0 und Yi1 beobachten werden, können wir direkt die Gruppendifferenz E[Y zwischen der Versuchsgruppe und der Basisgruppe berechnen i1|Ti=1]-E [Yi0|. Dieser Unterschied kann weiter verbessert werden. Die Demontage entspricht E[Yi1 |Ti=1]-E[Yi0|Ti=1] +E [Yi0 |T i=1]-E[Yi0|Ti=0]. Darunter ist E[Yi1|Ti=1]-E[Yi0|Ti=1] die Versuchsgruppe Einzelperson Der durchschnittliche Behandlungseffekt (ATT) im Test, ATT und ATE sind oft nicht gleich, und die Differenz zwischen den beiden stellt die von uns berechnete externe Validität dar. Wenn die Stichprobe auf Benutzer einer bestimmten Altersgruppe beschränkt ist, sind die Ergebnisse möglicherweise nicht auf Benutzer aller Altersgruppen übertragbar, was darauf hindeutet, dass unsere Analyse möglicherweise keine externe Validität aufweist. Der zweite Teil in der obigen Formel ist E[Yi0|Ti=1]-E[Yi0|Ti = 0] stellt den Selektivitätsbias der Probe dar. Im wirklichen Leben ist die Auswahlverzerrung möglicherweise häufig nicht 0. Wenn beispielsweise die experimentelle Gruppe und die Benchmark-Gruppe nicht zufällig ausgewählt werden und es Unterschiede in bestimmten Merkmalsverteilungen gibt, kann eine Auswahlverzerrung auftreten. Daher stellt der von uns berechnete Unterschied zwischen den Gruppen tatsächlich den durchschnittlichen Behandlungseffekt dar, den wir nur dann erwarten, wenn der Auswahlfehler beseitigt ist, externe Validität aufweist und auf einer großen und ausreichenden Stichprobe basiert. Die Denkmethode des potenziellen Effektmodells besteht tatsächlich darin, solche Bedingungen durch bestimmte Einstellungen und Modelle zu erreichen. Hinter seinen Ideen stehen auch relativ strenge mathematische Annahmen. Im Folgenden betrachten wir die wichtigsten Ideen sowie die technologische Entwicklung und Anwendungen der letzten Jahre nach verschiedenen Methoden. Aus Platzgründen wird die Breakpoint-Regressionsmethode hier nicht im Detail vorgestellt. 1. A/B-Tests
Die häufigste Methode des potenziellen Wirkungsmodells ist das randomisierte Experiment oder A/B-Testen, das wir in der Branche häufig verwenden. Wir haben die Versuchsgruppe und die Basisgruppe durch bestimmte Zufallsstichproben zusammengestellt, um die Unterschiede zwischen den Gruppen zu beobachten. Es sollte jedoch darauf hingewiesen werden, dass selbst wenn die Zufälligkeit erfüllt ist, die Wirksamkeit der kausalen Schlussfolgerung hier immer noch eine wichtige Annahme erfüllen muss – die Stable Unit Treatment Value Assumption (SUTVA). Die potenziellen Ergebnisse jedes Einzelnen sind nur für ihn selbst relevant und haben nichts damit zu tun, ob andere Personen durch die experimentelle Strategie interveniert werden. Gleichzeitig weist die einzelne strategische Intervention, um die es uns geht, keine unterschiedlichen Formen oder Intensitäten auf unterschiedliche mögliche Ergebnisse. Es gibt viele Szenarien, in denen SUTVA-Annahmen im wirklichen Leben verletzt werden, was auch die Entwicklung verschiedener neuer A/B-Testtechniken inspiriert hat, wie z. B. Budget- oder strategische Kontrolle bei Überfüllungsproblemen oder Verbesserungen im Umleitungsdesign. Hier geben wir einige Beispiele zum Thema Ablenkung:Bei LinkedIn verwenden Experimentatoren experimentelle Netzwerk-Sampling-Methoden, um die Herausforderungen zu bewältigen, die soziale Netzwerke für traditionelle individuelle Zufallsexperimente darstellen. Zunächst werden Benutzer in verschiedene Cluster eingeteilt, und jeder Cluster wird als Einzelperson verwendet, um experimentelle Indikatoren zufällig aufzuteilen und zu messen. Der geschätzte Behandlungseffekt wird durch Schätzung der Netzwerkeffektexposition des Benutzers korrigiert (Gui et al. 2015).
Auf Plattformen wie Airbnb kommt es häufig zu einer gegenseitigen Beeinflussung zwischen Käufern und Verkäufern, die auch traditionelle experimentelle Methoden beeinträchtigen kann. Forscher konstruieren experimentelle Bewertungsindikatoren durch bilaterales experimentelles Design und dynamische Bestandsmodelle (Johari et al. 2022). Es sollte darauf hingewiesen werden, dass bilaterale Experimente ein relativ neues Feld sind und ihr experimentelles Design den Experimentatoren helfen kann, die Spillover-Effekte traditioneller einseitiger Experimente zu entdecken. Es ist jedoch schwierig, statistische Schlussfolgerungen und Korrekturen zu experimentellen Ergebnissen zu ziehen, und dies ist möglicherweise auch nicht der Fall eine absolute Antwort. Es sollte mehr in Kombination mit Geschäftsszenarien diskutiert werden.
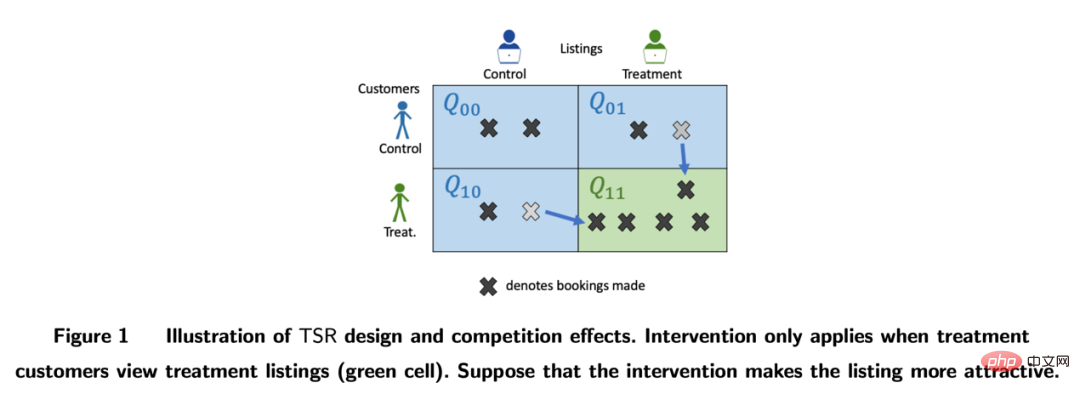
Bilder aus der Arbeit Johari et al. (2022)
2, Instrumentelle Variablenmethode
Instrumentelle Variablen sind eine Methode zum Lösen die Endogenität linearer Regressionsprobleme . Als nächstes stellen wir das Endogenitätsproblem vor und wie man Endogenität durch instrumentelle Variablen löst. Das Hauptproblem bei der Endogenität besteht darin, dass wir uns um die Auswirkung von X auf Y kümmern, es aber eine nicht gemessene Variable U gibt, die sowohl X als auch Y beeinflusst. Dann ist X endogen und U ist die oben erwähnte Störvariable. Wenn wir eine Variable Z finden können, die mit X zusammenhängt, und Z nicht mit U zusammenhängt. Dann können wir Z als Instrumentvariable verwenden, um den kausalen Effekt von X auf Y abzuschätzen. Die spezifische Berechnungsmethode ist im Allgemeinen die zweistufige Methode der kleinsten Quadrate. Wenn die Methode der instrumentellen Variablen tatsächlich verwendet wird, sollte darauf geachtet werden, das Problem „schwacher instrumenteller Variablen“ zu vermeiden, dh die Korrelation zwischen der instrumentellen Variablen Z und der interessierenden Variablen X ist sehr gering, was zu einer Verzerrung führen kann geschätzter kausaler Effekt Sie können sich auf statistische Testmethoden verlassen, um zu bestätigen, ob ein solches Problem vorliegt.
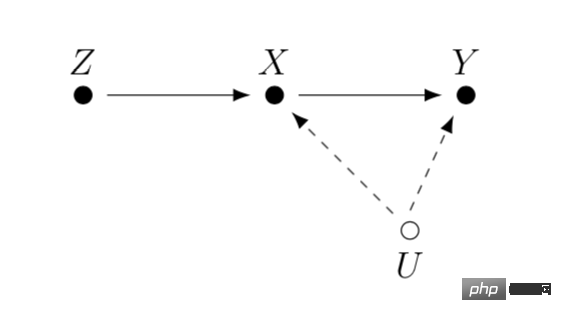
Eine Weiterentwicklung der instrumentellen Variablenmethode besteht darin, sie mit einem Deep-Learning-Modell zu kombinieren, wie beispielsweise der von Hartford et al. vorgeschlagenen Deep IV-Methode. Diese Forschung wandelt die traditionelle zweistufige Methode der kleinsten Quadrate instrumenteller Variablen in eine flexiblere Vorhersageaufgabe zweier tiefer neuronaler Netze um und lockert die starken Annahmen über den Datengenerierungsprozess (DGP) in der traditionellen Methode.
In tatsächlichen Anwendungen können wir basierend auf den Szenarien, die aus einer großen Anzahl von A/B-Tests im Internet gesammelt wurden, den kausalen Zusammenhang zwischen Indikatoren durch experimentelles Meta-Lernen und instrumentelle Variablenmethoden lernen. Beispielsweise verwendeten Peysakhovich & Eckles (2018) Facebook-Daten, nutzten die Informationen der Versuchsgruppe als instrumentelle Variable und kombinierten die L0-Regularisierung auf der Grundlage der zweistufigen Methode der kleinsten Quadrate, wodurch das Bias-Problem traditioneller instrumenteller Variablen gelöst werden kann Methode an begrenzten Proben und kann auch das Problem relativ niedriger absoluter Werte von Effekten („schwache Instrumentenvariablen“) überwinden, die in einer großen Anzahl von Experimenten in realen Situationen beobachtet werden.
Neben dem Erlernen der Einflussbeziehung zwischen Indikatoren kann die Idee instrumenteller Variablen auch zur Lösung des Bias-Problems in Empfehlungssystemen genutzt werden. In Empfehlungssystemen basiert das Modelltraining häufig auf den historischen Ansichten und dem Feedbackverhalten der Benutzer, aber diese historischen Daten werden häufig durch Störfaktoren wie den Anzeigeort und den Belichtungsmodus beeinflusst. Forscher der Kuaishou und Renmin University Si et al. Das IV4Rec-Framework nutzt die Idee instrumenteller Variablen und verwendet Suchabfragen als instrumentelle Variablen, um kausale und nicht kausale Beziehungen in das Empfehlungssystem einzubetten. In Kombination mit Deep Learning kann es sowohl für Kuaishou-Daten als auch für andere verwendet werden Der öffentliche Datensatz MIND. Überprüfen Sie den Effekt der Verbesserung des Empfehlungsmodells.
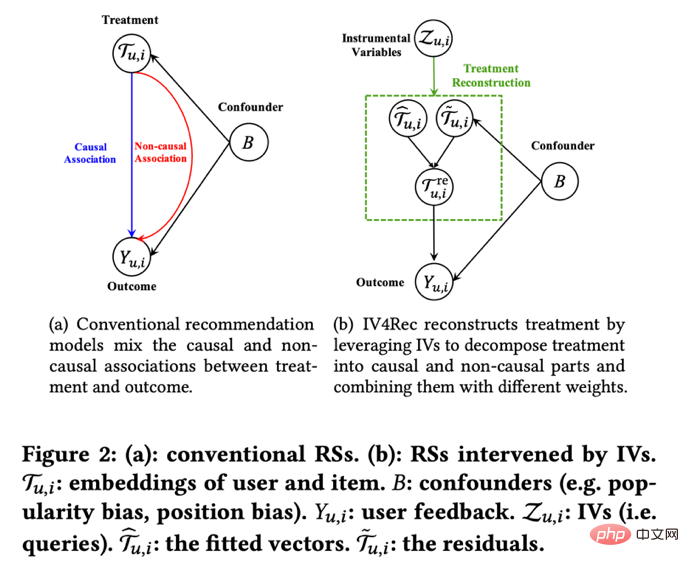
Bilder aus der Arbeit Si et al. (2022)
3. Matching-Methode
Matching ist eine kausale Analysemethode, die von Unternehmen häufig verwendet wird, hauptsächlich um das Problem zu lösen, wenn die Versuchsgruppe und die Kontrollgruppe aus irgendeinem Grund nicht vergleichbar sind (Störfaktor), indem jeder Benutzer abgeglichen wird in der Experimentalgruppe mit dem Benutzer in der Kontrollgruppe, der ihm in bestimmten Merkmalen am ähnlichsten ist (CEM-Coarse-Grained-Matching) oder die größte Wahrscheinlichkeit hat, eine Intervention zu erhalten (Propensity-Score) (PSM-Propensity-Score-Matching), um eine Vergleichbarkeit wiederherzustellen Versuchsgruppe und Kontrollgruppe. Matching ist die Methode, die dem Zufallsexperiment AB/RCT (randomisierte kontrollierte Studie) am ähnlichsten ist. Die Operationsmethode ist relativ ähnlich und die Ergebnisse sind sehr intuitiv. Darüber hinaus ist Matching eine nichtparametrische Methode zur Schätzung von Behandlungseffekten und unterliegt nicht den allgemeinen Annahmen des linearen parametrischen Modells. Durch Anpassen der Stichproben kann auch die Doppeldifferenzmethode verwendet werden, die häufig zur Lösung des Problems der geringen Penetrationsrate neuer Funktionen verwendet wird. In den letzten Jahren wurde die Entwicklung von Matching-Methoden hauptsächlich mit Modellen für maschinelles Lernen kombiniert, um den Neigungs-Score-Matching genauer zu machen. Gleichzeitig wurden die Ideen hier auch auf einige andere kausale Methoden und Modellkorrekturen für maschinelles Lernen angewendet wird später besprochen.
4. Serielle Methoden und Entwicklung von Paneldaten
In den letzten Jahren sind viele neue Methoden rund um die kausale Schlussfolgerung von Paneldaten entstanden. Sehen wir uns zunächst die traditionellen Paneldatenmethoden an.
Die am häufigsten verwendete Methode ist die Doppeldifferenzmethode. Die einfachste Differenz-in-Differenz besteht darin, die Differenz zwischen Gruppen zu kontrollieren und die Form eines Regressionsmodells zu verwenden, um yit=α0+α1Treati+α2 zu beschreiben Postt+α 3Treati*Postt. Hier stellt Treati=1 dar, ob die Person einer Intervention unterliegt, und Postt=1 stellt den Beobachtungszeitraum nach der Intervention dar. Aus der folgenden Tabelle können wir entnehmen, dass α2+α3 der Differenzwert der Versuchsgruppe vor und nach dem Versuchsdatum ist, α2 der Differenzwert der Kontrollgruppe vor und nach dem Differenzwert des Experimentdatums. Aufgrund der Differenz zwischen diesen beiden Elementen ist α3 die Schätzung des kausalen Effekts, der auch der Koeffizient des Interaktionsterms im obigen Modell ist und das Ergebnis zweier Differenzen ist.
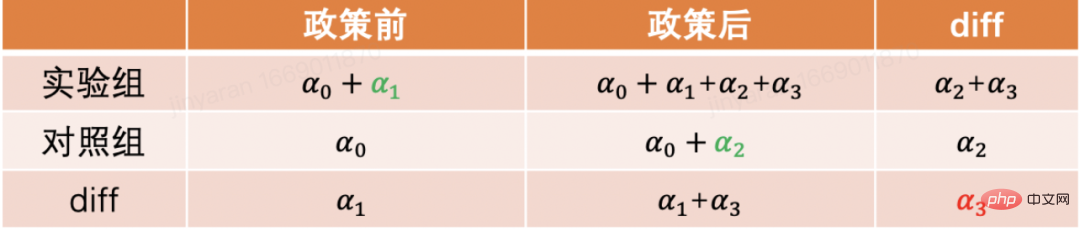
Die Differenz-in-Differenz-Methode basiert auf strengeren Annahmen. „Paralleltrend“ ist die wichtigste Prämisse, d. h. die Mittelwerte der Ergebnisindikatoren der experimentellen Gruppe und der Benchmark-Gruppe sind im Laufe der Zeit stabil Die Intervention selbst ist für die Experimentalgruppe und die Benchmark-Gruppe gleich. Wir können Zeittrenddiagramme verwenden, um parallele Hypothesen zu testen, und einige statistische Inferenzpakete bieten auch entsprechende Funktionen. Wenn der parallele Test fehlschlägt, können weitere Tests durchgeführt werden, indem der Regression Kontrollvariablen oder Zeittrendterme hinzugefügt werden. In einigen Fällen kann das Problem auch mithilfe der Dreifachdifferenzenmethode gelöst werden. Darüber hinaus gibt es in der Praxis viele Möglichkeiten, die Doppeldifferenzmethode umzusetzen. Zusätzlich zur oben genannten Methode ist das „Zwei-Wege-Fixed-Effects-Modell“ mit der Einstellung Yit=τTreatit+Xitβ+αi+ξt+ε it , Aber es beruht auch auf starken Annahmen: Es gibt keine Störfaktoren, die sich im Laufe der Zeit ändern, und vergangene Ergebnisse haben keinen Einfluss auf den aktuellen Behandlungsstatus. Außerdem muss der Behandlungseffekt der Richtlinie unverändert bleiben. Angesichts der Einschränkungen der dahinter stehenden Theorie und Methoden sowie der erweiterten neuen Methoden wie Matching und Reweighting wird empfohlen, in Kombination mit den Kursen von Professor Xu Yiqing von der Stanford University zu studieren:
https://yiqingxu.org/teaching /
Nachfolgend listen wir einige der am häufigsten verwendeten neuen Methoden auf:
Die synthetische Kontrollmethode ist eine Reihe von Methoden, die von der Paneldaten-Kausalinferenzmethode abgeleitet sind, und es entstehen ständig neue Forschungsergebnisse zu Schätzungen oder statistischen Inferenztests. Wenn die Intervention in einer Gruppe oder Region umgesetzt wird, hat die Versuchsgruppe zu einem Zeitpunkt nur einen Beobachtungswert und der Zeitraum der Daten ist lang, wie z. B. wenn eine Stadt lokale Werbeaktivitäten durchführt, normalerweise der Unterschied in- Die Differenzmethode ist derzeit nicht geeignet. Das Prinzip besteht darin, einige Kontrollstädte auszuwählen und sie in eine „virtuelle Kontrollgruppe“ einzuteilen, die der Versuchsgruppe vor der Intervention sehr ähnlich ist. Für eine detaillierte theoretische Einführung und Optimierung in den letzten Jahren wenden Sie sich bitte an Professor Aberto Abadie vom Massachusetts Institute of Technology und seine Mitarbeiter (Abadie, Diamond und Hainmueller 2010) und sein kurzer Kurs am NBER zum weiteren Studium:
https://www.nber.org/lecture/2021-summer-institute- Methoden-Vorlesung-Alberto-Abadie-Synthetische-Kontrollen-Methoden-und-Praxis
Die Methode der doppelten Differenz und die Methode der synthetischen Kontrolle können tatsächlich innerhalb eines analytischen Rahmensystems vereinheitlicht werden. Forschungen von Arkhangelsky et al. (2021) haben darauf hingewiesen, dass Differenz-in-Differenzen ein Zwei-Wege-Regressionsproblem mit festen Effekten ohne individuelle oder zeitliche Gewichtung lösen, während die synthetische Kontrollmethode das Gewicht ω auf Einzelpersonen anwendet, bevor die politische Intervention erfolgt, um sie anzupassen Für Einzelpersonen kombiniert dieses Papier zwei Methoden, um einen neuen Schätzer vorzuschlagen: die synthetische Doppeldifferenz (SDID), die sowohl das individuelle Gewicht ω als auch das Zeitgewicht λ umfasst und so die Robustheit des Gesamtschätzers verbessert. Das Gewicht der Zeit λ kann hier als der Datenzeitraum verstanden werden, der dem Zeitraum nach dem Eingriff ähnlicher ist und ein höheres Gewicht erhält.
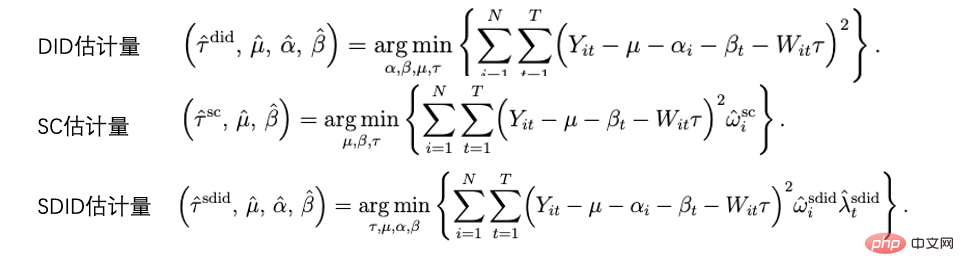
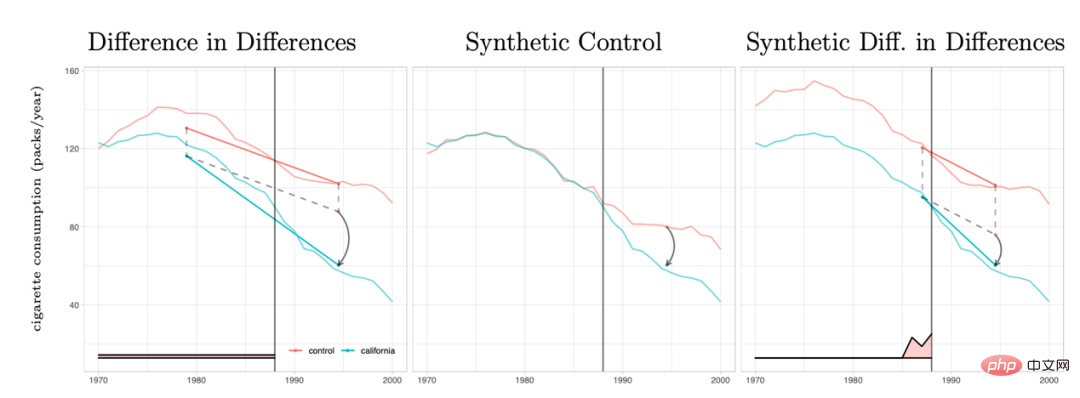
Vergleich mehrerer Methoden: Das Bild stammt aus der Arbeit Arkhangelsky et al. (2021)
Paneldaten können auch mit der Matrixvervollständigungsmethode für kausale Schlussfolgerungen kombiniert werden , was auch eine neue Entwicklung in diesem Bereich in den letzten Jahren darstellt. Der Matrixvervollständigungsalgorithmus löst das Problem fehlender kontrafaktischer Daten, mit dem kausale Schlussfolgerungen konfrontiert sind, indem er ein konvexes Optimierungsproblem löst. Diese Methode eignet sich für Situationen, in denen Einzelpersonen inkonsistenten Richtlinieninterventionszeiten unterliegen. Beispielsweise erfordert eine Iteration eines Produkts, dass Benutzer die Produktversion aktualisieren, um wirksam zu werden, die Benutzeraktualisierungszeiten sind jedoch inkonsistent. Für eine detaillierte Methodentheorie verweisen wir auf verwandte Veröffentlichungen wie Athey et al. Methoden zur Matrixvervollständigung, synthetischen Kontrolle und Regressionsvorhersage unter zufälliger Intervention können auch im Rahmen von Optimierungsproblemen vereinheitlicht werden, und wir können auch mehrere Methoden im Ensemble kombinieren, um robustere Schätzergebnisse zu erhalten (Athey et.al 2019).

Schematische Darstellung der Matrixvervollständigung: Das Bild stammt aus dem Kurs von Guidon Imbens an der AEA, wobei W den Behandlungsstatus darstellt https://www.aeaweb.org/conference/cont-ed/2018- Webcasts
Oben haben wir in diesem Abschnitt die wichtigsten Methoden und den Fortschritt der kausalen Schlussfolgerung aus Paneldaten vorgestellt. In diesem Bereich gibt es sehr unterschiedliche Methoden und sehr schnelle Fortschritte, aber es erfordert, dass Benutzer vollständig darüber nachdenken Gründe für die Annahmen und Einschränkungen können verwendet werden, um verschiedene Richtlinien in der Praxis genauer zu bewerten. Aus Platzgründen geben wir hier nur eine sehr kurze Einführung.
5. Eine Überprüfung der Methoden für heterogene kausale Effekte
Die Kombination maschineller Lernmethoden zur Untersuchung heterogener kausaler Effekte ist tatsächlich ein Trend in der Entwicklung kausaler Schlussfolgerungen in den letzten Jahren. Lassen Sie uns zunächst den heterogenen Kausaleffekt vorstellen: Der heterogene Behandlungseffekt (HTE) bezieht sich auf das Phänomen, dass Experimente aufgrund unterschiedlicher individueller Eigenschaften von Proben unterschiedliche Auswirkungen auf Einzelpersonen haben. In Kombination mit mathematischen Formeln ausgedrückt hat HTE viele Formen:
Der kausale Effekt ITE (individueller Behandlungseffekt) jedes Einzelnen: τi=Yi1-Yi0, nur einer von Yi1 und Yi0 kann beobachtet werden, der andere und τ i muss durch eine bestimmte Modellmethode geschätzt werden.
Der durchschnittliche kausale Effekt der Gruppe auf bestimmte Merkmale. Hier verwenden wir Effekt: τ(x)=E[Y1-Y0|X=x].
HTEs Analysemethode hat derzeit ein breites Spektrum an Anwendungsszenarien. Durch HTE können wir die Merkmale der Gruppen kennen, die am meisten auf eine bestimmte strategische Intervention reagieren. Es kann uns auch helfen, den Mechanismus einer A/B-Teststrategie zu untersuchen, die die erwartete Wirkung hat oder auch keine Wirkung hat auf verschiedene Personalisierungen unter den Strategien angewendet. Heterogene kausale Inferenzmethoden finden in der Industrie und im Internet viele Anwendungsmöglichkeiten. Microsoft nutzt diese Methode beispielsweise zur Messung des langfristigen ROI verschiedener Projekte gefunden Siehe KDD-Schulungskurs 2021 (https://causal-machine-learning.github.io/kdd2021-tutorial/).
Die gebräuchlichste Methode für heterogene kausale Effekte ist tatsächlich die in der experimentellen Analyse häufig verwendete mehrdimensionale Analyse. Die Verwendung der mehrdimensionalen Analyse erfordert jedoch sorgfältige Beachtung des Problems mehrerer Tests. Gleichzeitig sind bei ausreichender Dimensionierung die Anforderungen an die experimentelle Probengröße relativ hoch und die Analyseeffizienz relativ gering. Die maschinelle Lernmethode bietet einige Mining-Methoden, die die Effizienz verbessern. Ihr Vorteil besteht darin, dass sie die Verteilung heterogener Kausaleffekte adaptiv erlernen kann und keine strengen funktionalen Formannahmen erfordert. Sie ist besser als herkömmliche ökonometrische Methoden Methoden haben größere Freiheitsgrade, aber die technische Herausforderung besteht darin, statistische Schlussfolgerungen zu ziehen. In den letzten Jahren wurden mit der Vertiefung der Kombination von maschinellem Lernen und Ökonometrie viele Methodensätze in diesem Bereich innoviert und angewendet. Hier konzentrieren wir uns auf die folgenden Arten von Methoden. Bedingte Unabhängigkeitsannahme), das heißt, nur wenn verschiedene Störvariablen ausreichend kontrolliert werden, können wir relativ genaue Schätzungen der kausalen Effekte erhalten.
Kausaler Wald: Basierend auf dem Zufallswald handelt es sich um eine nichtparametrische Methode, die direkt eine Anpassungsschätzung durchführt. Die Hauptschätzlogik eines Kausalbaums besteht darin, die Verlustfunktion des Gesamtbaums durch Definition der Kausalwirkung auf jedem Blatt zu definieren. Der Kausalbaum zielt darauf ab, die Summe der Verluste aller Blätter gemäß einer bestimmten Art der Aufteilung von X zu maximieren. Zusätzlich zu den unterschiedlichen Schätzzielen von Baumalgorithmen beim maschinellen Lernen besteht ein weiterer Unterschied darin, dass Trainingssatzproben im Allgemeinen in Trainingssätze und Schätzsätze unterteilt werden. Der Trainingssatz wird für die Blattpartitionierung verwendet, und der Schätzsatz wird verwendet Verwendet Berechnen Sie den durchschnittlichen Behandlungseffekt für jeden Blattknoten nach dem Blättern. Der Vorteil des Kausalbaums besteht darin, dass die Ergebnisse sehr prägnant und leicht verständlich sind. Sie können durch Bucketing direkt erkennen, welche Personengruppen deutliche Unterschiede in den experimentellen Effekten aufweisen . In der Praxis wird jedoch empfohlen, kausale Zufallswälder zu verwenden (siehe Athey und Imbens 2016, Wager und Athey 2018). statistische Inferenzeigenschaften. Zur Erweiterung dieser Methode verweisen wir auf Forschungsarbeiten wie Athey, Tibshirani und Wager (2019) und Friedberg et al. (2020). Diese neuen Methoden können Probleme weiter bewältigen, wenn Störvariablen vorliegen, und die Ergebnisse reibungsloser schätzen .
Meta-Lernende: unterscheidet sich von Modellen, die Kausalbäume verwenden, um kausale Effekte direkt abzuschätzen. Es handelt sich um eine Art indirektes Schätzmodell: Es modelliert direkt die Ergebnisvariable Y. Daher kann Meta Learner den geschätzten HTE nicht direkt für statistische Schlussfolgerungen verwenden. In praktischen Anwendungen verwenden einige Forscher Bootstrap-Methoden, um dieses Problem zu lösen. Es gibt drei Arten von Meta-Learner-Schätzalgorithmen: T-Learner, S-Learner und X-Learner. Der grundlegende Unterschied zwischen den drei Methoden ist:
Die einfachste ist S-Learner. Es verwendet die dazwischenliegende Variable als charakteristische Variable für die einmalige Modellierung, die für Situationen geeignet ist, in denen Behandlungs- und Ergebnisvariablen stark korrelieren, da das Modell sonst die durch Änderungen der dazwischenliegenden Variablen verursachte Änderung des Ergebnisses nicht identifizieren kann;Die etwas kompliziertere Variante ist T-Learner. Es identifiziert kausale Effekte, indem es zwei Modelle dazu zwingt, Yi1 der Versuchsgruppe bzw. Yi0 der Kontrollgruppe zu lernen. Es eignet sich zur Verwendung, wenn die variablen Beobachtungswerte der Versuchsgruppe und der Kontrollgruppe größer sind und eher durchschnittlich, sonst wird das Modell stärker reguliert.
Daten. Gute Schätzung (siehe Künzel et al. 2019 für weitere Details).
Auf DML und DRL basierendes Schätzungsframework: Wir führen diese beiden Frameworks in Verbindung mit dem Econml-Tool von Microsoft ein:
https://www.microsoft.com/en-us /research /project/econml/
DML (Double Machine Learning) ist ein Framework, das Variablen flexibel verwirrt und die Beziehung zwischen Variablen und Ergebnisvariablen verarbeitet, wenn hochdimensionale Störvariablen vorhanden sind Bei der Schätzung des kausalen Effekts ist es hauptsächlich in zwei Schritte unterteilt: Der erste Schritt besteht darin, zwei (nicht unbedingt dieselben) Modelle für maschinelles Lernen zu verwenden, um die beiden bedingten Erwartungen E (Y | X, W) und E (T | X, W) zu schätzen. und dann den Rest nehmen. Hier sind sowohl X als auch W Störvariablen, aber nur X ist die relevante Variable in CATE. Der zweite Schritt besteht darin, ATE oder CATE basierend auf dem Residuum zu schätzen. Bei der Schätzung von CATE wird das Residuum von T-E(T|X,W) zur Schätzung mit einer Funktion θ(X) über X multipliziert. Informationen zur Schätzung der ATE finden Sie bei Chernozhukov et al. Econml bietet im zweiten Schritt viele Modelle zur Auswahl: LinearDML (unter Verwendung des OLS-Modells), DML (unter Verwendung eines benutzerdefinierten Modells), CausalForestDML (unter Verwendung eines kausalen Zufallswalds) ... Bei der Verwendung des DML-Frameworks müssen Sie darauf achten, ob die Mittelwerte der Restterme der beiden Modelle signifikant von 0 abweichen oder signifikant korrelieren. Wenn dies der Fall ist, bedeutet dies, dass die Störvariablen möglicherweise nicht ausreichend kontrolliert werden.
DRL-Framework basiert auf der Doubly Robust-Methode, die ebenfalls in zwei Schritte unterteilt ist. Der erste Schritt verwendet X, W, T, um Y vorherzusagen, und definiert den vorhergesagten Wert als gt (X,W); Der zweite Schritt verwendet ein Klassifizierungsmodell, um T vorherzusagen Es ist zu beachten, dass T hier eine diskrete Variable ist und gt(X,W) auf eine Art regressionsbasiertes Modell beschränkt. Nach dem zweistufigen Ergebnis wird eine angepasste Ergebnisvariable berechnet:
Dann befindet sich das angepasste Y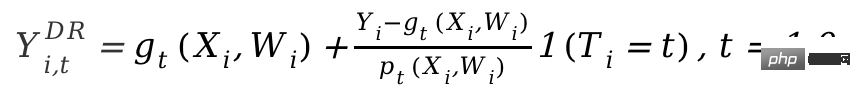
i,tDR in der Versuchsgruppe und der Kontrolle Gruppieren Sie die Differenz Yi1DR-Yi0DR und geben Sie X zurück, um CATE zu erhalten. Der Grund, warum DRL als doppelt robust bezeichnet wird, liegt darin, dass in der obigen Formel, solange eines von gt(X,W) und pt(X,W) korrekt ist, Der kausale Effekt wird geschätzt. Es ist unvoreingenommen. Wenn jedoch beide Modellschätzungen falsch sind, kann der resultierende Fehler sehr groß sein. Ähnlich wie bei DML besteht der Unterschied zwischen den verschiedenen DRL-Lernern in Econml darin, welche Art von Modell verwendet wird, um Y mit anzupassen.
Die größte Anwendungsherausforderung heterogener Kausalinferenzmethoden, die auf Modellen des maschinellen Lernens basieren, besteht tatsächlich darin, ein geeignetes Modell des maschinellen Lernens auszuwählen und Parameter anzupassen, um relativ robuste Schätzergebnisse zu erhalten. Basierend auf Anwendungserfahrungen und aktuellen Forschungsergebnissen gibt es folgende Vorsichtsmaßnahmen:
- Stellen Sie sicher, dass die Trainingsstichprobe groß genug ist.
-
Wenn Sie das Econml-Tool verwenden, wird empfohlen, die Score*-Funktion zur Auswahl des Modells zu verwenden (je kleiner der Score, desto besser das Modell), aber nicht jedes Modell verfügt über diese Funktion: zum Beispiel DML hat es, X-Learner oder Causal Forest jedoch nicht. Wenn Sie Causalml von Uber verwenden, können Sie das Cumulative Gain-Diagramm verwenden, um die Leistung verschiedener Meta-Lerner zu vergleichen.
https://github.com/uber/causalml.
- Einige Methoden können statistische Tests für HTE durchführen, andere jedoch nicht. In Econml sind die Methoden, die zur Durchführung statistischer Tests zu HTE verwendet werden können, auf die Methode beschränkt, das Last-Step-Modell in DML/DRL auf ein lineares Modell oder einen Kausalwald festzulegen, während dies auf die Merkmalsvariable X und die experimentelle Variable T zutrifft in vielen Geschäftsszenarien nichtlinear miteinander verbunden. Die erzwungene Wahl eines linearen Modells kann zu einer Verzerrung der HTE-Schätzung führen (z. B. hat die Volatilität von HTE nichts mit X zu tun und ist nur Rauschen). Wenn Personen mit signifikantem HTE für eine spätere Analyse gescreent werden sollen, ist eine mehrfache Testkorrektur für individuelle Effekttests erforderlich.
- Zusätzlich zum Grad der Modellanpassung ist ein Standard erforderlich, um die Qualität der HTE-Schätzung zu messen: Sie können beispielsweise feststellen, ob die Änderung des HTE groß genug ist, um sensible Gruppen von nicht sensiblen Gruppen zu unterscheiden Siehe die von Chernozhukov et al. (2018) vorgeschlagene Methode. Statistische Schlussfolgerungen basierend auf HTE-Merkmalen sind ebenfalls sehr einfach anzuwenden.
Die oben vorgestellten Methoden konzentrieren sich im Wesentlichen auf den statischen heterogenen Kausaleffekt unter einer dazwischenliegenden Variablen. In praktischen Anwendungen werden die Probleme jedoch komplexer sein. Beispielsweise sind mehrere intervenierende Variablen beteiligt: Die Subventionsanreize, die das Produkt den Benutzern bietet, können sowohl Anmeldeanreize als auch Belohnungen für andere Aufgaben umfassen. Die Ausgewogenheit der Verteilung verschiedener Arten von Anreizen kann als heterogene Kausalwirkungskonstruktion definiert werden mehrerer intervenierender Variablen. Ein weiteres Beispiel sind dynamische kausale Effekte, bei denen sich Störvariablen mit Intervention zu unterschiedlichen Zeitpunkten ändern (siehe Lewis und Syrgkanis 2020). Nehmen wir als Beispiel Anreizaufgaben. Diese Aufgaben können dazu führen, dass Benutzer auf neue Anker achten, wodurch sich ihre Präferenzen für die Anzeige von Inhalten ändern, und sie wirken sich auch auf die Wirkung nachfolgender Anreize aus. Diese komplexen Szenarien haben den weiteren Ausbau verschiedener Methoden inspiriert, und wir freuen uns auch auf die künftige Entwicklung etablierterer und systematischerer Forschungen und Anwendungen.
Strukturelles Kausalmodell
Im vorherigen Abschnitt haben wir die Hauptideen und die methodische Entwicklung latenter Ergebnismodelle vorgestellt. Diese Art von Schulmethode verfügt über eine relativ vollständige statistische Theorie und kann relativ genaue Schätzergebnisse erzielen. Es gibt jedoch bestimmte Einschränkungen, die nur zur Schätzung des Einflusses eines Korrelationsgrads zwischen Variablen verwendet werden können (d. h. es sind nur eine abhängige Variable und einige unabhängige Variablen zulässig, und Verbindungen indirekter Effekte können nicht geschätzt werden). Die Beziehung zwischen vielen Variablen. Verbindungen und komplexe Zusammenhänge erfordern den Einsatz einer anderen Schule struktureller Kausalmodellmethoden.
Das strukturelle Kausalmodell verwendet einen gerichteten azyklischen Graphen (DAG), um den Kausalzusammenhang und die bedingte Verteilung zwischen Variablen zu beschreiben. Jeder Knoten des Diagramms ist eine Variable, und der kausale Zusammenhang wird durch die Kanten dargestellt, die diese Knoten verbinden. Zum Beispiel X11 nennen wir auch X 1 ein untergeordneter Knoten und Für eine DAG, die aus einer Reihe von Zufallsvariablen X=(X1, P(X)=∏pj=1P( ist X Der unmittelbare übergeordnete Knoten von j. Wenn wir den Kausalzusammenhang ausdrücken, führen wir das Konzept des do-Operators ein, unter der Annahme, dass der aktuelle Wert ,...xp), use do(Xj=x ' j) repräsentiert den Eingriff für die Variable P(X1 =x1, p =xp|do(Xj=x 'j)) , die erwartete Änderung jeder anderen Variablen unter der alten und neuen Verteilung ist Die kausale Wirkung von auf sie, wie z j=xj)). Judea Pearl, der Begründer des Outcome-Causal-Modells, wies in seiner Forschung darauf hin, dass es bei der Verwendung von Kausaldiagrammen zur Identifizierung kausaler Zusammenhänge nicht unbedingt notwendig ist, alle Variablen zu beobachten, wenn das „Hintertürkriterium“ und das „Fronttürkriterium“ erfüllt sind. Bezüglich spezifischer theoretischer Details verweisen wir auf Pearl (2009). Es sollte hinzugefügt werden, dass das strukturelle Kausalmodell und das potenzielle Ergebnismodell tatsächlich miteinander verbunden sind. In praktischen Anwendungen verfügen wir möglicherweise nicht direkt über die Informationen, um einen Kausalgraphen zu definieren. Daher ist das Erlernen der Kausalgraphenstruktur zwischen Variablen zu einem wichtigen Thema geworden. Bei der Lösung dieser Art von Problem müssen wir zunächst die erforderlichen Annahmen klären:
Kausal-Markov-Kausal-Markov-Annahme: Diese Annahme bedeutet, dass die bedingte Verteilung eines Knotens nur auf seinem direkten übergeordneten Knoten basiert.
Annahme der kausalen Suffizienz: Diese Annahme entspricht dem Fehlen unbeobachteter Störvariablen.
Kausale Treue Annahme: Diese Annahme bedeutet, dass basierend auf einer bedingten Wahrscheinlichkeitsverteilung einige Knoten unabhängig voneinander sind (so dass der Graph geschnitten werden kann).
Die Algorithmen sind grob in zwei Kategorien unterteilt:
Eine ausführliche Einführung finden Sie in Glymour, Zhang und Sprites (2019) und im Artikel „Statistical Methods of Causal Inference“ in „Science China“. : Mathematik“ Ausgabe 12, 2018 》:
https://cosx.org/2022/10/causality-statistical-method/.
Einschränkungsbasierte Algorithmen: Lernen Sie alle Kausalgraphen, die die Treue- und Kausal-Markov-Annahmen erfüllen, basierend auf dem Unabhängigkeitstest der bedingten Verteilung, d. h. testen Sie, ob die bedingte Verteilung zwischen zwei Knoten unabhängig ist. Zum Beispiel PC-Algorithmus (Spirtes und Glymour 1991) und IC-Algorithmus (Verma und Pearl 1990).
Score-basierte Algorithmen: Finden Sie die Diagrammstruktur, die am besten zu den Daten passt, indem Sie einen bestimmten definierten Score optimieren. Strukturgleichungen und Score-Funktionen müssen definiert werden. Zum Beispiel der CGNN-Algorithmus (Goudet et al. 2017) und der NOTEARS-Algorithmus (Zheng et al. 2018). Hier konzentrieren wir uns auf den NOTEARS-Algorithmus. Der herkömmliche Algorithmus basiert auf allen Knoten und möglichen Beziehungen zwischen Knoten, sucht in allen möglichen Diagrammen und wählt die optimale Lösung gemäß einem bestimmten Standard aus. Dies ist ein typisches NP-schweres Problem und erfordert extrem viel Zeit und Strom Die Ressourcen sind grundsätzlich nicht in der Lage, den Rechenbedarf zu decken. Der NOTEARS-Algorithmus wandelt das diskrete Suchproblem in ein kontinuierliches Suchproblem um. Dieser Algorithmus verbessert die Rechengeschwindigkeit erheblich und macht ihn für normale Datenanalysten nutzbar. Allerdings weist diese Methode auch gewisse Einschränkungen auf. Beispielsweise wird davon ausgegangen, dass das Rauschen aller Variablen gaußverteilt sein muss. In den letzten Jahren haben immer mehr Methoden versucht, die Annahmen zu verbessern solche Methoden.
Mit der Entwicklung des Bereichs des verstärkenden Lernens haben wir auch festgestellt, dass kausale Schlussfolgerung und verstärkendes Lernen miteinander kombiniert werden können, um die Entwicklung des anderen zu fördern. Kausale Schlussfolgerungen können dazu beitragen, dass Algorithmen für verstärktes Lernen effizienter Wertfunktionen oder optimale Strategien erlernen, indem sie auf den Kausalzusammenhang zwischen Zuständen oder zwischen Zuständen und Aktionen beim verstärkten Lernen schließen. Leser, die sich für diesen Aspekt interessieren, können sich an Professor Elias Bareinboim von Columbia University Courses wenden. https://www.php.cn/link/ad16fe8f92f051afbf656271afd7872d). Andererseits kann Reinforcement Learning auch in den Lernalgorithmus von Kausalgraphen integriert werden, wie Zhu, Ng und Chen (2019) im Noah's Ark Laboratory von Huawei.
Was die Zukunftsaussichten der Kausalinferenz betrifft, sollten wir ein neues Forschungsparadigma im Zusammenhang mit Graphenlernen, Kausalinferenz und maschinellem Lernen erwähnen, das in den letzten Jahren vom Team von Professor Cui Peng vorgeschlagen wurde der Tsinghua-Universität (Cui und Athey 2022). Die Anwendung von Modellen wie maschinellem Lernen und künstlicher Intelligenz beruht auf einer wichtigen Annahme – der Annahme von unabhängig und identisch verteilt. Das heißt, der Trainingssatz und der Testsatz müssen aus derselben Verteilung stammen, tatsächlich gibt es jedoch verschiedene OOD-Probleme (Out Of Distribution, außerhalb der Verteilung). Derzeit kann die Leistung des Modells nicht garantiert werden Dies ist auch ein Problem, mit dem verschiedene Modelle in der Geschichte konfrontiert waren. Kausalschluss kann helfen, solche Probleme zu überwinden. Wenn garantiert werden kann, dass eine Struktur in verschiedenen Umgebungen den gleichen Vorhersageeffekt hat, um das OOD-Problem zu überwinden, muss diese Struktur eine kausale Struktur sein, und die Leistung einer kausalen Struktur in verschiedenen Umgebungen ist relativ stabil. Untersuchungen des Teams von Cui Peng (He et al. 2022, Shen et al. 2021) ergaben, dass mithilfe der Idee des verwirrenden Variablen-Matching-Balances alle Variablen durch Neugewichtung der Stichprobe unabhängig gemacht werden können, wodurch ein korrelationsbasiertes Modell entsteht auf Ursache und Wirkung basierendes Modell. Das sogenannte stabile Lernen besteht darin, einen Trainingssatz aus einer Verteilung und einen Testsatz aus mehreren verschiedenen unbekannten Verteilungen zu verwenden. Das Optimierungsziel besteht darin, die Varianz der Genauigkeit zu minimieren. Ich glaube, dass dies ein sehr wichtiges Zukunftsfeld ist und interessierte Leser weiterhin auf relevante Forschungsfortschritte achten können.
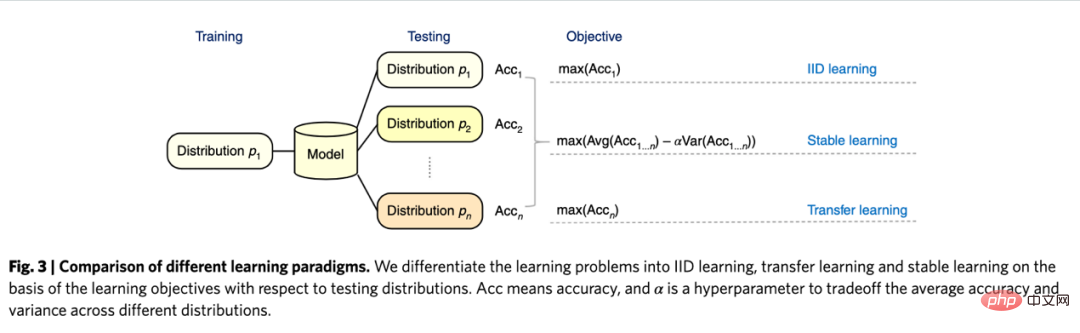
Vergleich von unabhängigem und identisch verteiltem Lernen, Transferlernen und stabilem Lernen: Bilder aus der Arbeit Cui und Athey 2022
In praktischen Anwendungen, Empfehlungssystemen, Computer Vision, automatischem Fahren , Natürlich Es gibt keinen Mangel an Kausalinferenz und Kausalgraphenlernen in Bereichen im Zusammenhang mit maschinellem Lernen und künstlicher Intelligenz, wie z. B. der Sprachverarbeitung, was die Entwicklung dieser Bereiche in den letzten Jahren vorangetrieben hat. Hier listen wir auch einige Beispiele für detailliertere Anwendungen auf Informationen zu Benchmark-Simulatoren und Datensätzen finden Sie in der Zusammenfassung von Forschern der UCL und der Universität Oxford (Kaddour et al. 2022). Im Bereich der Empfehlungssysteme weisen Empfehlungssysteme, wie wir sie bei der Anwendung instrumenteller Variablenmethoden eingeführt haben, zwangsläufig Verzerrungen auf. Die Identifizierung der kausalen Diagrammbeziehung zwischen Benutzern und Elementen kann dem Empfehlungssystem helfen, Verzerrungen zu korrigieren. Beispielsweise verwendeten Wang et al. (2021) und Zhang et al. (2021) kausale Diagramme, um die durch Clickbait bzw. Popularität verursachte Verzerrung zu beseitigen. Im Bereich des autonomen Fahrens haben Forscher von Microsoft CausalCity (McDuff et al. 2022) auf den Markt gebracht, eine Plattform für simulierte Fahrumgebungen, die kausale Schlussfolgerungen in die Vorhersage der Fahrzeugtrajektorie integriert. Im Bereich der Verarbeitung natürlicher Sprache haben Forscher herausgefunden, dass kausale Schlussfolgerungen dazu beitragen können, dass NLP-Methoden robuster und verständlicher werden (Zeng et al. 2020), einschließlich der Prüfung von Verzerrungen in Sprachmodellen und Korpora (Vig et al. 2020)... I glauben, dass die kausale Folgerung auch in Zukunft weiter florieren und in diesen und anderen Bereichen eine wichtige Rolle spielen wird.




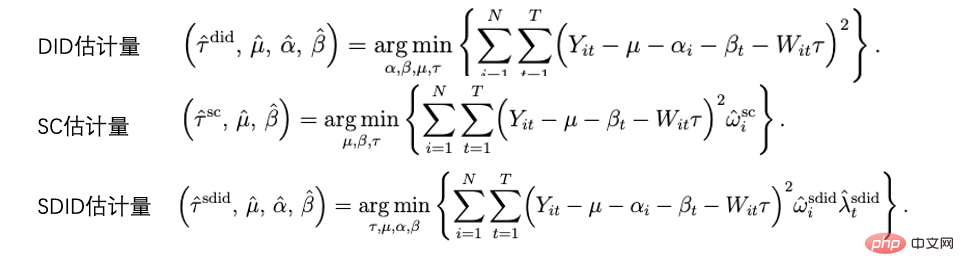


Die etwas kompliziertere Variante ist T-Learner. Es identifiziert kausale Effekte, indem es zwei Modelle dazu zwingt, Yi1 der Versuchsgruppe bzw. Yi0 der Kontrollgruppe zu lernen. Es eignet sich zur Verwendung, wenn die variablen Beobachtungswerte der Versuchsgruppe und der Kontrollgruppe größer sind und eher durchschnittlich, sonst wird das Modell stärker reguliert.
Daten. Gute Schätzung (siehe Künzel et al. 2019 für weitere Details).
Auf DML und DRL basierendes Schätzungsframework: Wir führen diese beiden Frameworks in Verbindung mit dem Econml-Tool von Microsoft ein:
https://www.microsoft.com/en-us /research /project/econml/
DML (Double Machine Learning) ist ein Framework, das Variablen flexibel verwirrt und die Beziehung zwischen Variablen und Ergebnisvariablen verarbeitet, wenn hochdimensionale Störvariablen vorhanden sind Bei der Schätzung des kausalen Effekts ist es hauptsächlich in zwei Schritte unterteilt: Der erste Schritt besteht darin, zwei (nicht unbedingt dieselben) Modelle für maschinelles Lernen zu verwenden, um die beiden bedingten Erwartungen E (Y | X, W) und E (T | X, W) zu schätzen. und dann den Rest nehmen. Hier sind sowohl X als auch W Störvariablen, aber nur X ist die relevante Variable in CATE. Der zweite Schritt besteht darin, ATE oder CATE basierend auf dem Residuum zu schätzen. Bei der Schätzung von CATE wird das Residuum von T-E(T|X,W) zur Schätzung mit einer Funktion θ(X) über X multipliziert. Informationen zur Schätzung der ATE finden Sie bei Chernozhukov et al. Econml bietet im zweiten Schritt viele Modelle zur Auswahl: LinearDML (unter Verwendung des OLS-Modells), DML (unter Verwendung eines benutzerdefinierten Modells), CausalForestDML (unter Verwendung eines kausalen Zufallswalds) ... Bei der Verwendung des DML-Frameworks müssen Sie darauf achten, ob die Mittelwerte der Restterme der beiden Modelle signifikant von 0 abweichen oder signifikant korrelieren. Wenn dies der Fall ist, bedeutet dies, dass die Störvariablen möglicherweise nicht ausreichend kontrolliert werden.
DRL-Framework basiert auf der Doubly Robust-Methode, die ebenfalls in zwei Schritte unterteilt ist. Der erste Schritt verwendet X, W, T, um Y vorherzusagen, und definiert den vorhergesagten Wert als gt (X,W); Der zweite Schritt verwendet ein Klassifizierungsmodell, um T vorherzusagen Es ist zu beachten, dass T hier eine diskrete Variable ist und gt(X,W) auf eine Art regressionsbasiertes Modell beschränkt. Nach dem zweistufigen Ergebnis wird eine angepasste Ergebnisvariable berechnet:
Dann befindet sich das angepasste Y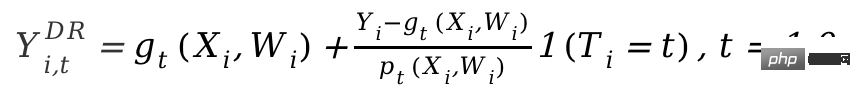
i,tDR in der Versuchsgruppe und der Kontrolle Gruppieren Sie die Differenz Yi1DR-Yi0DR und geben Sie X zurück, um CATE zu erhalten. Der Grund, warum DRL als doppelt robust bezeichnet wird, liegt darin, dass in der obigen Formel, solange eines von gt(X,W) und pt(X,W) korrekt ist, Der kausale Effekt wird geschätzt. Es ist unvoreingenommen. Wenn jedoch beide Modellschätzungen falsch sind, kann der resultierende Fehler sehr groß sein. Ähnlich wie bei DML besteht der Unterschied zwischen den verschiedenen DRL-Lernern in Econml darin, welche Art von Modell verwendet wird, um Y mit anzupassen.
Die größte Anwendungsherausforderung heterogener Kausalinferenzmethoden, die auf Modellen des maschinellen Lernens basieren, besteht tatsächlich darin, ein geeignetes Modell des maschinellen Lernens auszuwählen und Parameter anzupassen, um relativ robuste Schätzergebnisse zu erhalten. Basierend auf Anwendungserfahrungen und aktuellen Forschungsergebnissen gibt es folgende Vorsichtsmaßnahmen:
- Stellen Sie sicher, dass die Trainingsstichprobe groß genug ist.
-
Wenn Sie das Econml-Tool verwenden, wird empfohlen, die Score*-Funktion zur Auswahl des Modells zu verwenden (je kleiner der Score, desto besser das Modell), aber nicht jedes Modell verfügt über diese Funktion: zum Beispiel DML hat es, X-Learner oder Causal Forest jedoch nicht. Wenn Sie Causalml von Uber verwenden, können Sie das Cumulative Gain-Diagramm verwenden, um die Leistung verschiedener Meta-Lerner zu vergleichen.
https://github.com/uber/causalml. - Einige Methoden können statistische Tests für HTE durchführen, andere jedoch nicht. In Econml sind die Methoden, die zur Durchführung statistischer Tests zu HTE verwendet werden können, auf die Methode beschränkt, das Last-Step-Modell in DML/DRL auf ein lineares Modell oder einen Kausalwald festzulegen, während dies auf die Merkmalsvariable X und die experimentelle Variable T zutrifft in vielen Geschäftsszenarien nichtlinear miteinander verbunden. Die erzwungene Wahl eines linearen Modells kann zu einer Verzerrung der HTE-Schätzung führen (z. B. hat die Volatilität von HTE nichts mit X zu tun und ist nur Rauschen). Wenn Personen mit signifikantem HTE für eine spätere Analyse gescreent werden sollen, ist eine mehrfache Testkorrektur für individuelle Effekttests erforderlich.
- Zusätzlich zum Grad der Modellanpassung ist ein Standard erforderlich, um die Qualität der HTE-Schätzung zu messen: Sie können beispielsweise feststellen, ob die Änderung des HTE groß genug ist, um sensible Gruppen von nicht sensiblen Gruppen zu unterscheiden Siehe die von Chernozhukov et al. (2018) vorgeschlagene Methode. Statistische Schlussfolgerungen basierend auf HTE-Merkmalen sind ebenfalls sehr einfach anzuwenden.
Die oben vorgestellten Methoden konzentrieren sich im Wesentlichen auf den statischen heterogenen Kausaleffekt unter einer dazwischenliegenden Variablen. In praktischen Anwendungen werden die Probleme jedoch komplexer sein. Beispielsweise sind mehrere intervenierende Variablen beteiligt: Die Subventionsanreize, die das Produkt den Benutzern bietet, können sowohl Anmeldeanreize als auch Belohnungen für andere Aufgaben umfassen. Die Ausgewogenheit der Verteilung verschiedener Arten von Anreizen kann als heterogene Kausalwirkungskonstruktion definiert werden mehrerer intervenierender Variablen. Ein weiteres Beispiel sind dynamische kausale Effekte, bei denen sich Störvariablen mit Intervention zu unterschiedlichen Zeitpunkten ändern (siehe Lewis und Syrgkanis 2020). Nehmen wir als Beispiel Anreizaufgaben. Diese Aufgaben können dazu führen, dass Benutzer auf neue Anker achten, wodurch sich ihre Präferenzen für die Anzeige von Inhalten ändern, und sie wirken sich auch auf die Wirkung nachfolgender Anreize aus. Diese komplexen Szenarien haben den weiteren Ausbau verschiedener Methoden inspiriert, und wir freuen uns auch auf die künftige Entwicklung etablierterer und systematischerer Forschungen und Anwendungen.
Strukturelles Kausalmodell
Im vorherigen Abschnitt haben wir die Hauptideen und die methodische Entwicklung latenter Ergebnismodelle vorgestellt. Diese Art von Schulmethode verfügt über eine relativ vollständige statistische Theorie und kann relativ genaue Schätzergebnisse erzielen. Es gibt jedoch bestimmte Einschränkungen, die nur zur Schätzung des Einflusses eines Korrelationsgrads zwischen Variablen verwendet werden können (d. h. es sind nur eine abhängige Variable und einige unabhängige Variablen zulässig, und Verbindungen indirekter Effekte können nicht geschätzt werden). Die Beziehung zwischen vielen Variablen. Verbindungen und komplexe Zusammenhänge erfordern den Einsatz einer anderen Schule struktureller Kausalmodellmethoden.
Das strukturelle Kausalmodell verwendet einen gerichteten azyklischen Graphen (DAG), um den Kausalzusammenhang und die bedingte Verteilung zwischen Variablen zu beschreiben. Jeder Knoten des Diagramms ist eine Variable, und der kausale Zusammenhang wird durch die Kanten dargestellt, die diese Knoten verbinden. Zum Beispiel X11 nennen wir auch X 1 ein untergeordneter Knoten und Für eine DAG, die aus einer Reihe von Zufallsvariablen X=(X1, P(X)=∏pj=1P( ist X Der unmittelbare übergeordnete Knoten von j. Wenn wir den Kausalzusammenhang ausdrücken, führen wir das Konzept des do-Operators ein, unter der Annahme, dass der aktuelle Wert ,...xp), use do(Xj=x ' j) repräsentiert den Eingriff für die Variable P(X1 =x1, p =xp|do(Xj=x 'j)) , die erwartete Änderung jeder anderen Variablen unter der alten und neuen Verteilung ist Die kausale Wirkung von auf sie, wie z j=xj)). Judea Pearl, der Begründer des Outcome-Causal-Modells, wies in seiner Forschung darauf hin, dass es bei der Verwendung von Kausaldiagrammen zur Identifizierung kausaler Zusammenhänge nicht unbedingt notwendig ist, alle Variablen zu beobachten, wenn das „Hintertürkriterium“ und das „Fronttürkriterium“ erfüllt sind. Bezüglich spezifischer theoretischer Details verweisen wir auf Pearl (2009). Es sollte hinzugefügt werden, dass das strukturelle Kausalmodell und das potenzielle Ergebnismodell tatsächlich miteinander verbunden sind. In praktischen Anwendungen verfügen wir möglicherweise nicht direkt über die Informationen, um einen Kausalgraphen zu definieren. Daher ist das Erlernen der Kausalgraphenstruktur zwischen Variablen zu einem wichtigen Thema geworden. Bei der Lösung dieser Art von Problem müssen wir zunächst die erforderlichen Annahmen klären: Kausal-Markov-Kausal-Markov-Annahme: Diese Annahme bedeutet, dass die bedingte Verteilung eines Knotens nur auf seinem direkten übergeordneten Knoten basiert. Annahme der kausalen Suffizienz: Diese Annahme entspricht dem Fehlen unbeobachteter Störvariablen. Kausale Treue Annahme: Diese Annahme bedeutet, dass basierend auf einer bedingten Wahrscheinlichkeitsverteilung einige Knoten unabhängig voneinander sind (so dass der Graph geschnitten werden kann). Die Algorithmen sind grob in zwei Kategorien unterteilt: Eine ausführliche Einführung finden Sie in Glymour, Zhang und Sprites (2019) und im Artikel „Statistical Methods of Causal Inference“ in „Science China“. : Mathematik“ Ausgabe 12, 2018 》: https://cosx.org/2022/10/causality-statistical-method/. Einschränkungsbasierte Algorithmen: Lernen Sie alle Kausalgraphen, die die Treue- und Kausal-Markov-Annahmen erfüllen, basierend auf dem Unabhängigkeitstest der bedingten Verteilung, d. h. testen Sie, ob die bedingte Verteilung zwischen zwei Knoten unabhängig ist. Zum Beispiel PC-Algorithmus (Spirtes und Glymour 1991) und IC-Algorithmus (Verma und Pearl 1990). Score-basierte Algorithmen: Finden Sie die Diagrammstruktur, die am besten zu den Daten passt, indem Sie einen bestimmten definierten Score optimieren. Strukturgleichungen und Score-Funktionen müssen definiert werden. Zum Beispiel der CGNN-Algorithmus (Goudet et al. 2017) und der NOTEARS-Algorithmus (Zheng et al. 2018). Hier konzentrieren wir uns auf den NOTEARS-Algorithmus. Der herkömmliche Algorithmus basiert auf allen Knoten und möglichen Beziehungen zwischen Knoten, sucht in allen möglichen Diagrammen und wählt die optimale Lösung gemäß einem bestimmten Standard aus. Dies ist ein typisches NP-schweres Problem und erfordert extrem viel Zeit und Strom Die Ressourcen sind grundsätzlich nicht in der Lage, den Rechenbedarf zu decken. Der NOTEARS-Algorithmus wandelt das diskrete Suchproblem in ein kontinuierliches Suchproblem um. Dieser Algorithmus verbessert die Rechengeschwindigkeit erheblich und macht ihn für normale Datenanalysten nutzbar. Allerdings weist diese Methode auch gewisse Einschränkungen auf. Beispielsweise wird davon ausgegangen, dass das Rauschen aller Variablen gaußverteilt sein muss. In den letzten Jahren haben immer mehr Methoden versucht, die Annahmen zu verbessern solche Methoden. Mit der Entwicklung des Bereichs des verstärkenden Lernens haben wir auch festgestellt, dass kausale Schlussfolgerung und verstärkendes Lernen miteinander kombiniert werden können, um die Entwicklung des anderen zu fördern. Kausale Schlussfolgerungen können dazu beitragen, dass Algorithmen für verstärktes Lernen effizienter Wertfunktionen oder optimale Strategien erlernen, indem sie auf den Kausalzusammenhang zwischen Zuständen oder zwischen Zuständen und Aktionen beim verstärkten Lernen schließen. Leser, die sich für diesen Aspekt interessieren, können sich an Professor Elias Bareinboim von Columbia University Courses wenden. https://www.php.cn/link/ad16fe8f92f051afbf656271afd7872d). Andererseits kann Reinforcement Learning auch in den Lernalgorithmus von Kausalgraphen integriert werden, wie Zhu, Ng und Chen (2019) im Noah's Ark Laboratory von Huawei. Was die Zukunftsaussichten der Kausalinferenz betrifft, sollten wir ein neues Forschungsparadigma im Zusammenhang mit Graphenlernen, Kausalinferenz und maschinellem Lernen erwähnen, das in den letzten Jahren vom Team von Professor Cui Peng vorgeschlagen wurde der Tsinghua-Universität (Cui und Athey 2022). Die Anwendung von Modellen wie maschinellem Lernen und künstlicher Intelligenz beruht auf einer wichtigen Annahme – der Annahme von unabhängig und identisch verteilt. Das heißt, der Trainingssatz und der Testsatz müssen aus derselben Verteilung stammen, tatsächlich gibt es jedoch verschiedene OOD-Probleme (Out Of Distribution, außerhalb der Verteilung). Derzeit kann die Leistung des Modells nicht garantiert werden Dies ist auch ein Problem, mit dem verschiedene Modelle in der Geschichte konfrontiert waren. Kausalschluss kann helfen, solche Probleme zu überwinden. Wenn garantiert werden kann, dass eine Struktur in verschiedenen Umgebungen den gleichen Vorhersageeffekt hat, um das OOD-Problem zu überwinden, muss diese Struktur eine kausale Struktur sein, und die Leistung einer kausalen Struktur in verschiedenen Umgebungen ist relativ stabil. Untersuchungen des Teams von Cui Peng (He et al. 2022, Shen et al. 2021) ergaben, dass mithilfe der Idee des verwirrenden Variablen-Matching-Balances alle Variablen durch Neugewichtung der Stichprobe unabhängig gemacht werden können, wodurch ein korrelationsbasiertes Modell entsteht auf Ursache und Wirkung basierendes Modell. Das sogenannte stabile Lernen besteht darin, einen Trainingssatz aus einer Verteilung und einen Testsatz aus mehreren verschiedenen unbekannten Verteilungen zu verwenden. Das Optimierungsziel besteht darin, die Varianz der Genauigkeit zu minimieren. Ich glaube, dass dies ein sehr wichtiges Zukunftsfeld ist und interessierte Leser weiterhin auf relevante Forschungsfortschritte achten können. Vergleich von unabhängigem und identisch verteiltem Lernen, Transferlernen und stabilem Lernen: Bilder aus der Arbeit Cui und Athey 2022 In praktischen Anwendungen, Empfehlungssystemen, Computer Vision, automatischem Fahren , Natürlich Es gibt keinen Mangel an Kausalinferenz und Kausalgraphenlernen in Bereichen im Zusammenhang mit maschinellem Lernen und künstlicher Intelligenz, wie z. B. der Sprachverarbeitung, was die Entwicklung dieser Bereiche in den letzten Jahren vorangetrieben hat. Hier listen wir auch einige Beispiele für detailliertere Anwendungen auf Informationen zu Benchmark-Simulatoren und Datensätzen finden Sie in der Zusammenfassung von Forschern der UCL und der Universität Oxford (Kaddour et al. 2022). Im Bereich der Empfehlungssysteme weisen Empfehlungssysteme, wie wir sie bei der Anwendung instrumenteller Variablenmethoden eingeführt haben, zwangsläufig Verzerrungen auf. Die Identifizierung der kausalen Diagrammbeziehung zwischen Benutzern und Elementen kann dem Empfehlungssystem helfen, Verzerrungen zu korrigieren. Beispielsweise verwendeten Wang et al. (2021) und Zhang et al. (2021) kausale Diagramme, um die durch Clickbait bzw. Popularität verursachte Verzerrung zu beseitigen. Im Bereich des autonomen Fahrens haben Forscher von Microsoft CausalCity (McDuff et al. 2022) auf den Markt gebracht, eine Plattform für simulierte Fahrumgebungen, die kausale Schlussfolgerungen in die Vorhersage der Fahrzeugtrajektorie integriert. Im Bereich der Verarbeitung natürlicher Sprache haben Forscher herausgefunden, dass kausale Schlussfolgerungen dazu beitragen können, dass NLP-Methoden robuster und verständlicher werden (Zeng et al. 2020), einschließlich der Prüfung von Verzerrungen in Sprachmodellen und Korpora (Vig et al. 2020)... I glauben, dass die kausale Folgerung auch in Zukunft weiter florieren und in diesen und anderen Bereichen eine wichtige Rolle spielen wird. 
Das obige ist der detaillierte Inhalt vonZusammenfassung der wichtigsten technischen Ideen und Methoden der kausalen Schlussfolgerung. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Technologietrends, die Sie im Jahr 2023 im Auge behalten sollten
- Wie künstliche Intelligenz Rechenzentrumsteams neue Alltagsaufgaben beschert
- Können künstliche Intelligenz oder Automatisierung das Problem der geringen Energieeffizienz in Gebäuden lösen?
- OpenAI-Mitbegründer im Interview mit Huang Renxun: Die Argumentationsfähigkeiten von GPT-4 haben noch nicht die Erwartungen erfüllt
- Dank der OpenAI-Technologie übertrifft Bing von Microsoft Google im Suchverkehr

