Heim >Technologie-Peripheriegeräte >KI >Das Training von ViT und MAE reduziert den Rechenaufwand um die Hälfte! Sea und die Peking-Universität haben gemeinsam den effizienten Optimierer Adan vorgeschlagen, der für tiefe Modelle verwendet werden kann
Das Training von ViT und MAE reduziert den Rechenaufwand um die Hälfte! Sea und die Peking-Universität haben gemeinsam den effizienten Optimierer Adan vorgeschlagen, der für tiefe Modelle verwendet werden kann
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2023-04-11 21:40:011676Durchsuche
Seit Google Vision Transformer (ViT) vorgeschlagen hat, ist ViT nach und nach zum Standard-Rückgrat für viele visuelle Aufgaben geworden. Mit der ViT-Struktur wurde SoTA für viele visuelle Aufgaben weiter verbessert, einschließlich Bildklassifizierung, Segmentierung, Erkennung, Erkennung usw.
ViT zu trainieren ist jedoch nicht einfach. Abgesehen davon, dass komplexere Trainingstechniken erforderlich sind, ist der für das Modelltraining erforderliche Rechenaufwand häufig viel größer als bei früheren CNNs. Kürzlich haben die Forschungsteams des Singapore Sea AI LAB (SAIL) und des Peking University ZERO Lab gemeinsam einen neuen „Deep Model Optimizer Adan“ vorgeschlagen, der das ViT-Training mit nur „der halben Berechnungsmenge“ abschließen kann.
 Papier-Link: https://arxiv.org/pdf/2208.06677.pdf
Papier-Link: https://arxiv.org/pdf/2208.06677.pdf
Code-Link: https://github.com/sail-sg/Adan
Darüber hinaus kann Adan mit dem gleichen Rechenaufwand mehrere Szenarien (einschließlich CV, NLP, RL
), mehrere Trainingsmethoden (überwacht und selbstüberwacht) undverschiedene Netzwerkstrukturen/Algorithmen( Swin , ViT, ResNet, ConvNext, MAE, LSTM, BERT, Transformer-XL, PPO-Algorithmus) haben alle Leistungsverbesserungen erzielt. Der Code, die Konfigurationsdateien und die Trainingsprotokolle sind alle Open Source.
Trainingsparadigma und Optimierer von Deep ModelsMit der Einführung von ViT sind die Trainingsmethoden von Deep Models immer komplexer geworden. Zu den gängigen Trainingstechniken gehören komplexe Datenverbesserung (wie MixUp, CutMix, AutoRand), Etikettenverarbeitung (wie Etikettenglättung und Rauschetikett), gleitender Durchschnitt von Modellparametern, zufällige Netzwerktiefe, Dropout usw. Durch die gemischte Anwendung dieser Techniken wurden die Verallgemeinerung und Robustheit des Modells verbessert, gleichzeitig ist jedoch auch die rechnerische Komplexität des Modelltrainings immer größer geworden.
Auf ImageNet 1k ist die Anzahl der Trainingsepochen von 90, die gerade von ResNet vorgeschlagen wurden, auf 300 gestiegen, die häufig für das Training von ViT verwendet werden. Selbst bei einigen selbstüberwachten Lernmodellen wie MAE und ViT hat die Anzahl der Epochen vor dem Training 1,6.000 erreicht. Die Erhöhung der Ausbildungsepoche bedeutet, dass die Ausbildungszeit stark verlängert wird, was die Kosten für akademische Forschung oder industrielle Umsetzung stark erhöht. Eine derzeit gängige Lösung besteht darin, die Trainingsbatchgröße zu erhöhen und das parallele Training zu unterstützen, um die Trainingszeit zu verkürzen. Das damit verbundene Problem besteht jedoch darin, dass eine große Batchgröße oft einen Leistungsabfall bedeutet, und je größer die Batchgröße, desto offensichtlicher die Situation.
Das liegt vor allem daran, dass die Anzahl der Modellparameteraktualisierungen mit zunehmender Batchgröße stark abnimmt. Der aktuelle Optimierer kann unter komplexen Trainingsparadigmen mit einer kleinen Anzahl von Aktualisierungen kein schnelles Training des Modells erreichen, was den Anstieg der Anzahl der Modelltrainingsepochen weiter erschwert.
Gibt es also einen neuen Optimierer, der tiefe Modelle schneller und besser mit weniger Parameteraktualisierungen trainieren kann? Kann dadurch nicht nur die Anzahl der Trainingsepochen reduziert werden, sondern auch die negativen Auswirkungen einer zunehmenden Batchgröße abgemildert werden?
Ignorierter ImpulsUm die Konvergenzgeschwindigkeit des Optimierers zu beschleunigen, ist die Einführung eines Impulses der direkteste Weg. Die in den letzten Jahren vorgeschlagenen Deep-Model-Optimierer folgen alle dem in Adam verwendeten Impulsparadigma –
Heavy-Ball-Methode:
wobei g_k das Zufallsrauschen, m_k das Moment und eta die Lernrate ist. Adam änderte die Aktualisierung von m_k von der kumulativen Form in die Form des gleitenden Durchschnitts und führte das Moment zweiter Ordnung (n_k) ein, um die Lernrate zu skalieren, nämlich:
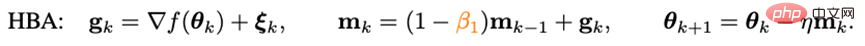
Da es Adam jedoch nicht gelang, das ursprüngliche ViT zu trainieren, wurde seine verbesserte Version AdamW nach und nach die erste Wahl für das Training von ViT und sogar ConvNext. AdamW ändert jedoch nicht das Impulsparadigma in Adam. Wenn also die Stapelgröße 4.096 überschreitet, sinkt die Leistung des von AdamW trainierten ViT stark. Auf dem Gebiet der traditionellen konvexen Optimierung gibt es eine Impulstechnik, die ebenso berühmt ist wie die Heavy-Ball-Methode – Nesterov-Impulsalgorithmus: Der Nesterov-Impulsalgorithmus weist eine gute Leistung bei glatten Bewegungen auf und im Allgemeinen konvexe Probleme. Es hat eine schnellere theoretische Konvergenzgeschwindigkeit als die Heavy-Ball-Methode und kann theoretisch größeren Chargengrößen standhalten. Anders als bei der gewichteten Kugelmethode berechnet der Nesterov-Algorithmus nicht den Gradienten am aktuellen Punkt, sondern verwendet den Impuls, um einen Extrapolationspunkt zu finden, und akkumuliert dann den Impuls, nachdem der Gradient an diesem Punkt berechnet wurde. Extrapolationspunkte können dem Nesterov-Algorithmus dabei helfen, die geometrischen Informationen um den aktuellen Punkt im Voraus wahrzunehmen. Diese Eigenschaft macht den Nesterov-Impuls besser für komplexe Trainingsparadigmen und Modellstrukturen (wie ViT) geeignet, da er sich nicht einfach auf vergangene Impulse verlässt, um scharfe lokale Minimalpunkte zu umgehen, sondern diese durch Beobachtung der umgebenden Gradienten im Voraus anpasst. Obwohl der Nesterov-Impulsalgorithmus gewisse Vorteile hat, wurde er in Tiefenoptimierern selten angewendet und erforscht. Einer der Hauptgründe ist, dass der Nesterov-Algorithmus den Gradienten am Extrapolationspunkt berechnen und am aktuellen Punkt aktualisieren muss. Während dieser Zeit sind mehrere Modellparameter-Neuladungen und eine künstliche Rückausbreitung (BP) am Extrapolationspunkt erforderlich. Diese Unannehmlichkeiten schränken die Anwendung des Nesterov-Impulsalgorithmus in Tiefmodelloptimierern erheblich ein. Durch die Kombination des neu geschriebenen Nesterov-Impulses mit dem adaptiven Optimierungsalgorithmus und der Einführung eines entkoppelten Gewichtsabfalls kann der endgültige Adan-Optimierer erhalten werden. Mithilfe von Extrapolationspunkten kann Adan die umgebenden Gradienteninformationen im Voraus wahrnehmen und so scharfe lokale Minimalbereiche effizient umgehen, um die Verallgemeinerung des Modells zu erhöhen. 1) Adaptiver Nesterow-Impuls Der umgeschriebene Nesterov-Impulsalgorithmus entspricht dem ursprünglichen Algorithmus. Die Iterationspunkte der beiden können ineinander umgewandelt werden, und die endgültigen Konvergenzpunkte sind dieselben. Es ist ersichtlich, dass durch die Einführung des Differentialterms des Gradienten eine manuelle Parameterüberladung und ein künstlicher BP am Extrapolationspunkt vermieden werden können. Kombinieren Sie den neu geschriebenen Nesterov-Impulsalgorithmus mit dem adaptiven Klassenoptimierer – ersetzen Sie die Aktualisierung von m_k von der kumulativen Form zur Form des gleitenden Durchschnitts und verwenden Sie das Moment zweiter Ordnung, um die Lernrate zu skalieren: Jetzt haben wir die Basisversion von Adans Algorithmus erhalten. 2) Impuls der Gradientendifferenz Es kann festgestellt werden, dass die Aktualisierung von m_k den Gradienten und den Gradientenunterschied koppelt, in tatsächlichen Szenarien ist es jedoch häufig erforderlich, die beiden Elemente mit unterschiedlichen physikalischen Werten zu verarbeiten Bedeutungen getrennt, daher führten die Forscher den Impuls v_k der Gradientendifferenz ein: Hier werden unterschiedliche Impuls-/Durchschnittskoeffizienten für den Impuls des Gradienten und den Impuls seiner Differenz festgelegt. Der Gradientendifferenzterm kann die Aktualisierung des Optimierers verlangsamen, wenn benachbarte Gradienten inkonsistent sind, und umgekehrt die Aktualisierung beschleunigen, wenn die Gradientenrichtungen konsistent sind. 3) Entkoppelter Gewichtsverlust Für die Zielfunktion mit L2-Gewichtsregularisierung hat der derzeit beliebte AdamW-Optimierer eine bessere Leistung bei ViT und ConvNext erzielt, indem er L2-Regularisierung und Trainingsverlust entkoppelt. Allerdings ist die von AdamW verwendete Entkopplungsmethode heuristisch ausgerichtet und es gibt derzeit keine theoretische Garantie für ihre Konvergenz. Basierend auf der Idee der Entkopplung der L2-Regelmäßigkeit wird Adan auch eine entkoppelte Gewichtsabnahmestrategie vorgestellt. Gegenwärtig kann jede Iteration von Adan als Minimierung einer Annäherung erster Ordnung an das Optimierungsziel F angesehen werden: Da die L2-Gewichtsregularisierung in F zu einfach und glatt ist, besteht keine Notwendigkeit, sie auszuführen eine Näherung erster Ordnung. Daher können Sie nur eine Annäherung erster Ordnung an den Trainingsverlust vornehmen und die L2-Gewichtsregelmäßigkeit ignorieren. Dann lautet die letzte Iteration von Adan: Interessanterweise kann festgestellt werden, dass das Aktualisierungskriterium von AdamW ist das Adan-Aktualisierungskriterium in einer Näherung erster Ordnung, wenn die Lernrate eta nahe bei 0 liegt. Daher kann Adan oder sogar AdamW aus der Perspektive des proximalen Operators eine vernünftige Erklärung anstelle der ursprünglichen heuristischen Verbesserung gegeben werden. 4) Adan-Optimierer Kombinieren Sie die beiden Verbesserungen 2) und 3) in der Basisversion von Adan, und Sie können den folgenden Adan-Optimierer erhalten. Adan kombiniert die Vorteile des adaptiven Optimierers, des Nesterov-Impulses und der entkoppelten Gewichtsabfallstrategie, kann größeren Lernraten und Stapelgrößen standhalten und eine dynamische L2-Regularisierung von Modellparametern implementieren. 5. Konvergenzanalyse Die Konvergenzgeschwindigkeit des Adan-Optimierers kann bei nichtkonvexen stochastischen Optimierungsproblemen die bekannte theoretische Untergrenze erreichen, und diese Schlussfolgerung gilt auch bei einer entkoppelten Gewichtsabfallstrategie. Experimentelle Ergebnisse1. CV-Szenario
1) Überwachtes Lernen – ViT-Modell Es ist ersichtlich, dass Adan beispielsweise auf ViT-small, ViT-base, Swin-tiny und Swin-base nur die Hälfte der Rechenressourcen verbraucht, um Ergebnisse zu erzielen, die dem SoTA-Optimierer nahe kommen. und bei gleichem Rechenaufwand zeigt Adan bei beiden ViT-Modellen große Vorteile. Darüber hinaus wurde die Leistung von Adan auch bei großen Chargengrößen getestet:
Es ist ersichtlich, dass Adan bei verschiedenen Chargengrößen eine gute Leistung erbringt und relativ für große Chargengrößen ausgelegt ist. Der Optimierer ( LAMM) hat auch gewisse Vorteile. 2) Überwachtes Lernen – CNN-Modell
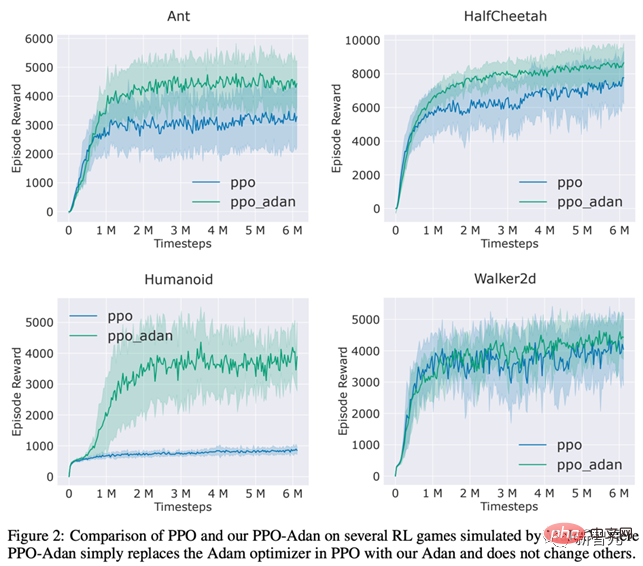
Zusätzlich zum schwieriger zu trainierenden ViT-Modell testeten die Forscher Adans Leistung auch auf CNN-Modellen mit relativ wenigen scharfen lokalen Minimalpunkten – einschließlich des klassischen ResNet und des fortgeschritteneren ConvNext. Die Ergebnisse sind wie folgt: Es kann beobachtet werden, dass Adan unabhängig von ResNet oder ConvNext innerhalb von etwa 2/3 der Trainingsepoche eine Leistung erzielen kann, die über SoTA hinausgeht. 3) Unüberwachtes Lernen Unter dem unüberwachten Trainingsrahmen testeten die Forscher die Leistung von Adan auf dem neu vorgeschlagenen MAE. Die Ergebnisse sind wie folgt: In Übereinstimmung mit der Schlussfolgerung des überwachten Lernens verbraucht Adan nur die Hälfte der Berechnungsmenge, um dem ursprünglichen SoTA-Optimierer zu entsprechen oder ihn sogar zu übertreffen, und wenn die Trainingsepoche kleiner wird, wird Adans Vorteil größer Je offensichtlicher es ist. 1) Überwachtes Lernen Beobachten Sie Adans Leistung beim klassischen LSTM und dem fortgeschrittenen Transformer-XL. Adan hat in den beiden oben genannten Netzwerken eine konstante Überlegenheit gezeigt. Und für Transformer-XL hat Adan den Standard-Adam-Optimierer in der Hälfte der Trainingsschritte gebunden. 2) Unüberwachtes Lernen Um Adans Modelltraining an unbeaufsichtigten Aufgaben in NLP-Szenarien zu testen. Die Forscher trainierten BERT von Grund auf: Nach 1000.000 Iterationen vor dem Training wurde die Leistung des von Adan trainierten Modells an 7 Teilaufgaben des GLUE-Datensatzes getestet, und die Ergebnisse sind wie folgt: Adan schnitt gut ab die 7 getestet Es zeigt große Vorteile bei Wort- und Satzklassifizierungsaufgaben. Es ist erwähnenswert, dass die Ergebnisse des von Adan trainierten BERT-Basismodells bei einigen Teilaufgaben (wie RTE, CoLA und SST-2) sogar das von Adam trainierte BERT-Large-Modell übertrafen. Die Forscher ersetzten den Optimierer im PPO-Algorithmus, der üblicherweise in RL verwendet wird, durch Adan und testeten die Leistung von Adan bei 4 Spielen in der MuJoCo-Engine. In 4 Spielen kann der PPO-Algorithmus, der Adan als Netzwerkoptimierer verwendet, immer höhere Belohnungen erzielen. Adan zeigt auch großes Potenzial im RL-Netzwerktraining. Der Adan-Optimierer führt ein neues Impulsparadigma für aktuelle Deep-Model-Optimierer ein. Erzielen Sie ein schnelles Training von Modellen unter komplexen Trainingsparadigmen mit weniger Aktualisierungen. Experimente zeigen, dass Adan mit nur 1/2-2/3 des Berechnungsaufwands dem bestehenden SoTA-Optimierer gleichkommen kann. Adan wird in mehreren Szenarien (einschließlich CV, NLP, RL), mehreren Trainingsmethoden (überwacht und selbstüberwacht) und mehreren Netzwerkstrukturen (ViT, CNN, LSTM, Transformer usw.) weisen alle große Leistungsvorteile auf. Darüber hinaus hat die Konvergenzgeschwindigkeit des Adan-Optimierers die theoretische Untergrenze bei der nichtkonvexen stochastischen Optimierung erreicht. 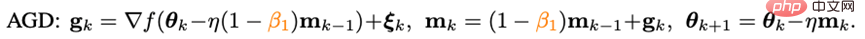
Adan-Optimierer
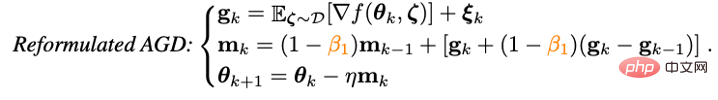
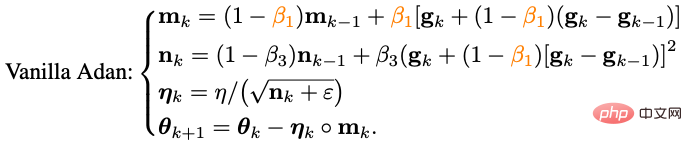
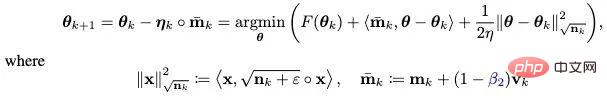
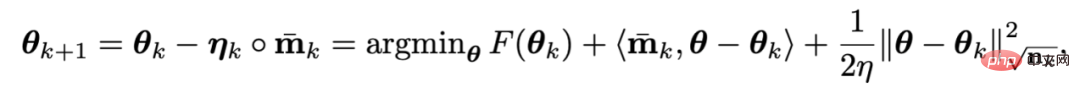

Für das ViT-Modell testeten die Forscher es jeweils an den Strukturen von ViT Leistung.

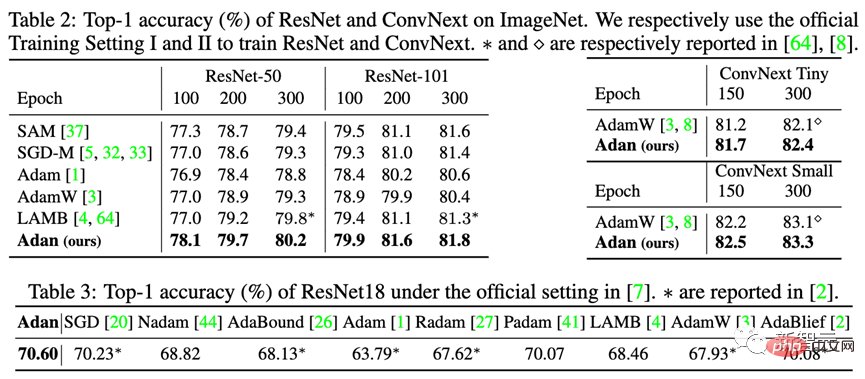

2. NLP-Szenario
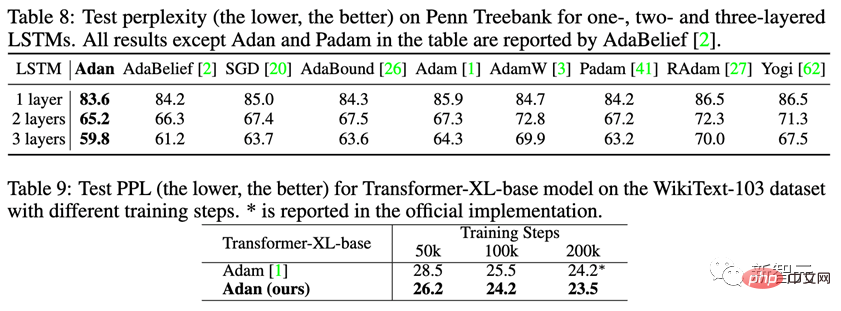

III RL-Szenario
Fazit und Ausblick
Das obige ist der detaillierte Inhalt vonDas Training von ViT und MAE reduziert den Rechenaufwand um die Hälfte! Sea und die Peking-Universität haben gemeinsam den effizienten Optimierer Adan vorgeschlagen, der für tiefe Modelle verwendet werden kann. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Technologietrends, die Sie im Jahr 2023 im Auge behalten sollten
- Wie künstliche Intelligenz Rechenzentrumsteams neue Alltagsaufgaben beschert
- Können künstliche Intelligenz oder Automatisierung das Problem der geringen Energieeffizienz in Gebäuden lösen?
- OpenAI-Mitbegründer im Interview mit Huang Renxun: Die Argumentationsfähigkeiten von GPT-4 haben noch nicht die Erwartungen erfüllt
- Dank der OpenAI-Technologie übertrifft Bing von Microsoft Google im Suchverkehr

