Die Effizienz der Animationsproduktion wurde um 80 % gesteigert! Diese KI-Software realisiert hochpräzise Video-Bewegungserfassung mit einem Klick

AIGC hat eine neue Magie!

Es ist keine Hand des Animators, keine Gewohnheitserfassung oder Lichterfassung erforderlich. Stellen Sie einfach ein Video bereit und diese KI-Bewegungserfassungssoftware kann die Aktion automatisch ausgeben. In nur wenigen Minuten ist die Animation des virtuellen Menschen abgeschlossen.

Nicht nur die großformatigen Bewegungen der Gliedmaßen, sondern auch die Details der Hände können präzise erfasst werden.

Zusätzlich zu Einzelansichtsvideos kann diese Software auch Mehrfachansichtsvideos unterstützen, die nur die Monokularerkennung unterstützen.

Gleichzeitig unterstützt die Software auch die Bearbeitung und Änderung erkannter Schlüsselpunkte des menschlichen Körpers, Glätte, Schrittdetails usw. Es kann alles befriedigen, vom Erfahrungsinteresse gewöhnlicher Spieler bis hin zu den professionellen Bedürfnissen von Hardcore-Spielern.

Dies ist die AIxPose-Video-Motion-Capture-Software, die seit vielen Jahren von NetEase Interactive Entertainment AI Lab entwickelt, kontinuierlich iterativ optimiert und auf Basis von professionellem Kunst-Feedback zurückhaltend gestaltet wird. Es wird berichtet, dass die Software mehr als Dutzende Stunden an Videoressourcen verarbeitet hat und im Produktionsprozess von Spielplot-Animationen, beliebten Tanzanimationen und anderen Ressourcen verwendet wurde. Durch tatsächliche Projekte wurde bestätigt, dass die Produktion einer 1-minütigen Tanzanimation von Hand mehr als 20 Tage dauern kann, die Produktion mit AIxPose-Unterstützung jedoch nur 3 Tage dauert und der gesamte Prozess um mehr als 80 % verkürzt wird.

Kürzlich hat NetEase Interactive Entertainment AI Lab die Erfahrungen basierend auf der Entwicklung dieser Software und damit verbundenen Forschungsarbeiten im Bereich der Bewegungserfassung zusammengestellt. Das von ihm verfasste Papier „Learning Analytical Posterior Probability for Human Mesh Recovery“ wurde veröffentlicht Computer Vision Akzeptanz von CVPR 2023.

• Homepage-Adresse: https://netease-gameai.github.io/ProPose/
• Papieradresse: https://netease-gameai.github.io/ProPose/static /assets/CVPR2023_ProPose.pdf

Dieses Papier schlägt innovativ eine auf Posterior-Wahrscheinlichkeit basierende Video-Motion-Capture-Technologie vor, mit der unter verschiedenen Einstellungen wie Einzelbild- und Multisensor-Fusion genaue dreidimensionale Bilder erzielt werden können Schätzung. Die technische Genauigkeit ist 19 % höher als die probabilistischen Basismethoden, die Prioritäten verwenden, und übertrifft frühere Methoden in den öffentlichen Datensätzen 3DPW, Human3.6M und AGORA. Darüber hinaus kann diese Technologie bei Multisensor-Fusionsaufgaben auch eine höhere Genauigkeit als das Basismodell erreichen, ohne das Rückgrat des neuronalen Netzwerks aufgrund der Einführung neuer Sensoren zu verändern.

Technischer Hintergrund

Die Aufgabe dieser Forschung besteht darin, die Wiederherstellung menschlicher Netze (HMR) anhand von RGB-Bildern vorherzusagen: direkte Methoden und indirekte Methoden. Die direkte Methode verwendet ein neuronales Netzwerk, um die Rotationsdarstellung menschlicher Gelenke von Ende zu Ende zu regressieren (z. B. Achsenwinkel, Rotationsmatrix, 6D-Vektor usw.), während die indirekte Methode zunächst einige Zwischendarstellungen vorhersagt (z. B. drei- Dimensionsschlüsselpunkte, Segmentierung usw.) und übergibt dann diese Zwischenpunkte. Zeigt an, dass die Gelenkdrehung erhalten wird.

Bei beiden Methodenarten gibt es jedoch einige Probleme. Bei direkten Methoden erfordert diese Art von Methode, dass das Netzwerk abstrakte Darstellungen wie Rotation direkt lernt. Im Vergleich zum Lernen von Schlüsselpunkten und Segmentierung ist das Lernen von Rotation relativ schwierig, sodass die vom Netzwerk ausgegebenen Ergebnisse manchmal schwer mit dem Bild in Einklang zu bringen sind und können nicht vollständig ausgeführt werden, z. B. der rechte Fuß in der ersten Reihe im Bild unten (a). Im Gegensatz dazu liefern indirekte Methoden im Allgemeinen eine höhere Genauigkeit, aber die Leistung dieser Art von Methode hängt stark von der Genauigkeit der Zwischendarstellung ab. Wenn die Zwischendarstellung aufgrund von Rauschen Fehler erzeugt, kann es leicht passieren, dass die endgültige Drehung ziemlich offensichtlich erscheint. Fehler, wie auf der linken Seite der zweiten Zeile in (b) unten gezeigt.

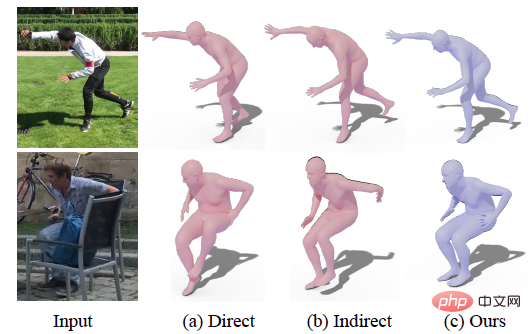
Zusätzlich zu den oben genannten deterministischen Methoden gibt es auch einige Methoden, um den menschlichen Körper durch das Erlernen bestimmter Wahrscheinlichkeiten zu modellieren Verteilungen Die Unsicherheit der Einstellung wird berücksichtigt, um die Systemrobustheit zu verbessern. Derzeit umfassen die wichtigsten Wahrscheinlichkeitsmodellierungsmethoden die multivariate Gaußsche Verteilung, den normalisierten Fluss, die implizite Modellierung neuronaler Netzwerke usw., aber diese Wahrscheinlichkeitsverteilungen auf Nicht-SO (3) können die Unsicherheit der Gelenkrotation nicht wirklich widerspiegeln. Wenn beispielsweise die Unsicherheit groß ist, gilt die Annahme der lokalen Linearität der Gaußschen Verteilung auf SO (3) nicht. In einer kürzlich durchgeführten Arbeit wurde das Netzwerk direkt verwendet, um die Parameter der Fisher-Verteilung der Matrix zu lernen. Obwohl es sich um eine Verteilung auf SO (3) handelt, ähnelt die Lernmethode dieser Methode der direkten Methode und die Konvergenzleistung kann nicht mit der verglichen werden bestehende indirekte Methode.

Um sowohl hohe Genauigkeit als auch Robustheit zu berücksichtigen und die Leistung probabilistischer Methoden zu verbessern, leitet ProPose die analytische Posteriorwahrscheinlichkeit der Gelenkrotation ab, was nicht nur Vorteile bringen kann aus verschiedenen Beobachtungen. Die hohe Präzision, die Variablen mit sich bringen, kann auch die Unsicherheit messen und den Einfluss von Rauschen auf den Algorithmus so weit wie möglich reduzieren. Wie in der folgenden Abbildung gezeigt, kann ProPose für das Eingabebild die Unsicherheit der Gelenkdrehung in verschiedene Richtungen anhand der Ausgabewahrscheinlichkeitsverteilung bis zu einem gewissen Grad messen, z. B. die Drehung der rechten Hand entlang der Armachse und die Richtung der linke Arm schwingt auf und ab und die linke Wade. Der Grad der Distanz usw.

Technische Umsetzung

Human Modeling​

# 🎜🎜#Diese Studie führt eine probabilistische Modellierung der menschlichen Körperhaltung durch. Ziel ist es, die hintere Wahrscheinlichkeit p (R|d,⋯) der Gelenkrotation R unter einigen beobachteten variablen Bedingungen (z. B. Knochenausrichtung d usw.) zu ermitteln.

Insbesondere, da die Gelenkrotation des menschlichen Körpers auf SO (3) liegt und die Einheitsknochenausrichtung des Kindgelenks relativ zum Elterngelenk lokalisiert ist auf S^2, daher kann die Analyse basierend auf Wahrscheinlichkeitsverteilungen auf diesen beiden Mannigfaltigkeiten durchgeführt werden.

Zunächst kann die Matrix-Fisher-Verteilung MF (⋅) auf SO (3) als vorherige Verteilung der Gelenkrotation R verwendet werden, wie in gezeigt Nach der folgenden Formel sind F∈R^ (3×3) die Parameter der Verteilung, c (F) ist eine Normalisierungskonstante und tr stellt die Spur der Matrix dar.

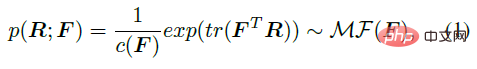
Wie in der folgenden Formel gezeigt, kann F direkt nach gelöst werden Mittelwert M durch SVD-Zerlegung und einen Aggregationsterm K, der den Grad der Verteilungsaggregation charakterisiert. Unter diesen ist Δ=diag (1,1,|UV|) eine diagonale orthogonale Matrix, die verwendet wird, um sicherzustellen, dass die Determinante von M 1 ist, sodass sie in die spezielle orthogonale Gruppe fallen kann.

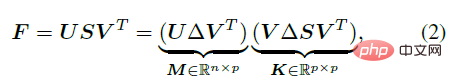
Zweitens, wenn man bedenkt, dass die Ausrichtung des Knochens durch das Gelenk berechnet werden kann Daher kann die Gelenkrotation R als versteckte Variable und die Knochenorientierung d als beobachtete Variable betrachtet werden. Unter der gegebenen Bedingung von R folgt die Einheitsorientierung d auf S^2 der von Mises-Fisher-Verteilung: # 🎜🎜##🎜 🎜#

wobei κ∈R und d∈S^2 der Aggregationsterm sind bzw. Mittelwert der Verteilung, und l ist die Referenz. Die Einheitsknochenausrichtung in einer Haltung (z. B. T-Pose) erfüllt theoretisch Rl=d, das heißt, die Referenzknochenausrichtung wird durch Gelenkrotation auf die aktuelle Knochenausrichtung übertragen.

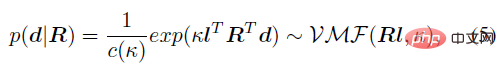
Mit der Bayes'schen Theorie können Sie unter Berücksichtigung der Prior-Verteilung p (R) und der Wahrscheinlichkeitsfunktion p (d|R) die Knochenorientierungsbedingung berechnen. Die analytische Form von die A-Posteriori-Wahrscheinlichkeit p (R|d) der Gelenkrotation: Daraus lässt sich schließen, dass die A-posteriori-Wahrscheinlichkeit p (R|d) ebenfalls der Matrix-Fisher-Verteilung folgt und ihre Parameter von F auf F^'=F+κdl^T aktualisiert werden.

Die obige hintere Wahrscheinlichkeit berücksichtigt nur die Ausrichtung des menschlichen Skeletts als Beobachtungsgröße. Ebenso kann sie auch auf andere Richtungsbeobachtungsgrößen d_i oder Rotationsbeobachtungsgrößen erweitert werden D_j (kann durch (von anderen Sensoren wie IMUs usw. erzeugt) gegeben werden. Die analytische A-Posteriori-Wahrscheinlichkeit wird in der folgenden allgemeinen Form erhalten:

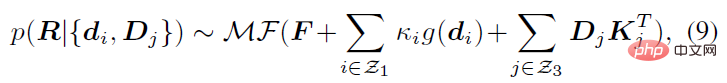
wobei κ_i und K_j Aggregationsterme sind. g (⋅) ist eine Abbildung in Form von IK, die Richtungsbeobachtungen in Rotationsschätzungen umwandeln kann. Sie kann die einfachste Form wie g (d_i)=dl^T annehmen. Z_1 und Z_3 repräsentieren den Satz von Richtungsbeobachtungen bzw. Rotationsbeobachtungen.

Eigenschaften

In diesem Abschnitt wird weiter erläutert, dass die hintere Wahrscheinlichkeitsverteilung einen höheren Aggregationsgrad aufweist als die vorherige Wahrscheinlichkeitsverteilung.

Im vorangegangenen Abschnitt wurde die analytische Form der hinteren Wahrscheinlichkeit der menschlichen Gelenkrotation vorgestellt, die durch einen neuen Parameter F‘ gekennzeichnet ist. Der hintere Parameter F^' kann aus einer anderen Perspektive verstanden werden, das heißt, F^' ist das Produkt des mittleren Termes M, der mit F identisch ist, und einem neuen Aggregationsterm K^':

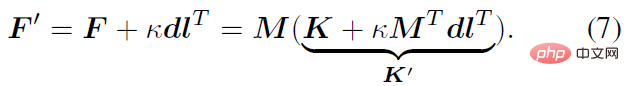
wo M^T dl^ T=ll^T ist eine reelle symmetrische Matrix vom Rang 1, und K ist ebenfalls eine reelle symmetrische Matrix, das heißt, der hintere Aggregationsterm K' ist ebenfalls eine reelle symmetrische Matrix. Gemäß dem gestaffelten Satz über reelle symmetrische Matrizen in der Matrixanalyse kann erhalten werden, dass die Eigenwerte λ_i' von K' und die Eigenwerte λ_i von K die folgende Ungleichheitsbeziehung aufweisen:

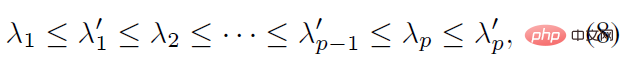
In Anbetracht dessen Die Eigenwerte der Aggregationsterme entsprechen der Verteilung. Die Singulärwerte der Parameter können die Konfidenz der Verteilung widerspiegeln. Daraus kann geschlossen werden, dass die hintere Schätzung größer ist, wenn der Wahrscheinlichkeitsterm ungleich Null ist konzentrierter als die vorherige Schätzung und kann schnell zum Likelihood-Funktionspräferenzmodus konvergieren, sodass er leichter erlernt werden kann.

Zusätzlich zur A-priori-Wahrscheinlichkeitsmethode besteht eine weitere wichtige Benchmark-Methode darin, die Rotation direkt durch die Knochenausrichtung zu berechnen. Das folgende Bild kann intuitiv den Unterschied zwischen der posterioren Wahrscheinlichkeitsmethode und der deterministischen IK zeigen Methode. Kontrast zwischen.

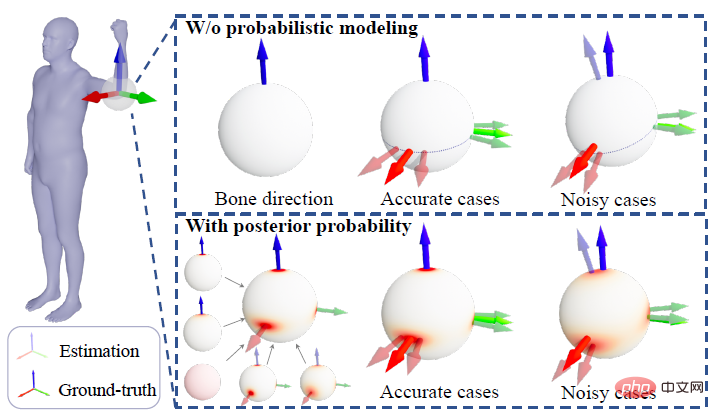
Das obige Bild nimmt das menschliche Ellenbogengelenk als Beispiel. Die reale dreidimensionale Koordinatenachse repräsentiert den wahren Wert und die transparente dreidimensionale Koordinatenachse repräsentiert den geschätzten Wert. Die erste Zeile stellt die deterministische IK-Methode dar. Die Modellierungsmethode hinter dieser Art von Methode ist ein Vektor, der die Knochenausrichtung darstellt. Wenn die Knochenausrichtung genau geschätzt wird, kann der verbleibende Freiheitsgrad (Twist) auf einen Kreis reduziert werden die Abbildung Der gepunktete Kreis auf der Kugel); wenn die Knochenausrichtung ungenau geschätzt wird, führt dies dazu, dass alle möglichen Schätzungen vom wahren Wert abweichen. Die zweite Linie stellt das hintere Wahrscheinlichkeitsmodell dieser Studie dar, das eine Fusion mehrerer verschiedener Modelltypen darstellt. Der rote Bereich auf der Kugel stellt die Wahrscheinlichkeit einer bestimmten Rotation dar, selbst wenn bei der Schätzung der Knochenausrichtung ein Fehler vorliegt , kann diese Methode den wahren Zustandswert wiederherstellen, da das Rauschen der Knochenausrichtung durch A-priori- oder andere Beobachtungen so weit wie möglich gemildert werden kann.

Netzwerk-Framework-Diagramm und Verlustfunktion

Basierend auf der oben genannten Theorie und Ableitung kann das in der folgenden Abbildung gezeigte Framework-Diagramm direkt erstellt werden. Ein Netzwerk mit mehreren Zweigen wird verwendet, um den vorherigen Verteilungsparameter F, den dreidimensionalen Schlüsselpunkt J (aus dem die Knochenorientierung d berechnet wird) und den Formparameter β aus einem einzelnen Bild zu schätzen. Die Posterior-Wahrscheinlichkeit wird mithilfe der Bayes-Regel berechnet, und schließlich kann die Haltungsschätzung aus der Posterior-Verteilung erhalten werden, um das menschliche Netz auszugeben.

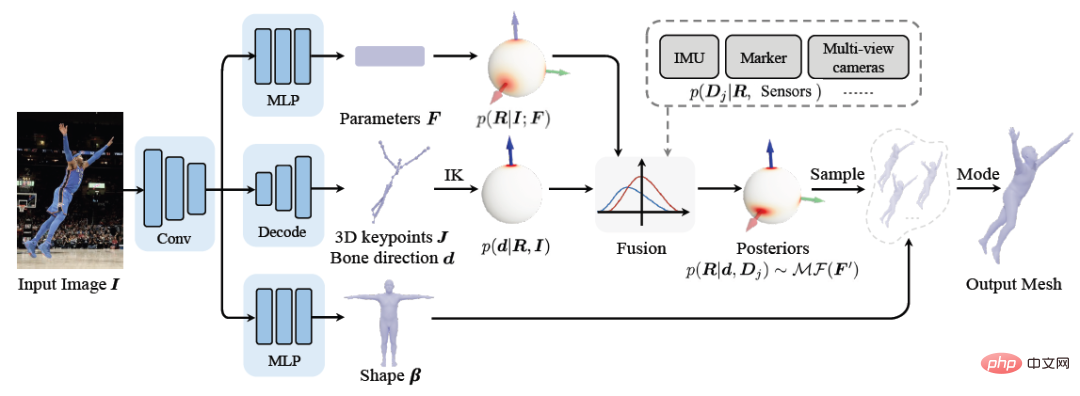
Die Auswahl der Verlustfunktion ist relativ einfach und stellt die gewichtete Summe der folgenden vier Einschränkungen dar, wobei L_J die Schlüsselpunktbeschränkung, L_β die Formparameterbeschränkung und L_θ die Lageparameterbeschränkung in der Matrix darstellt Form, und L_s repräsentiert die Verteilung der Post-Sampling-Pose-Beschränkungen. Bezüglich der Einschränkungen der Verteilung wird MAP hier nicht direkt verwendet, da die numerische Stabilität der Normalisierungsparameter berücksichtigt wird. In Bezug auf die Stichprobenstrategie wird die Fisher-Matrixverteilung ähnlich wie in der vorherigen Arbeit in die äquivalente Bingham-Verteilung in Quaternionform umgewandelt und dann durch Ablehnungsstichprobe erhalten, wobei die empfohlene Verteilung für die Ablehnungsstichprobe die eckige zentrale Gaußsche Verteilung annimmt.

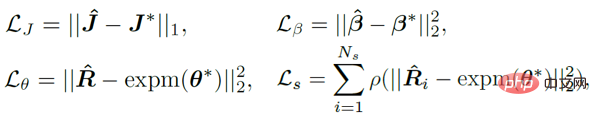
Experimentelle Ergebnisse

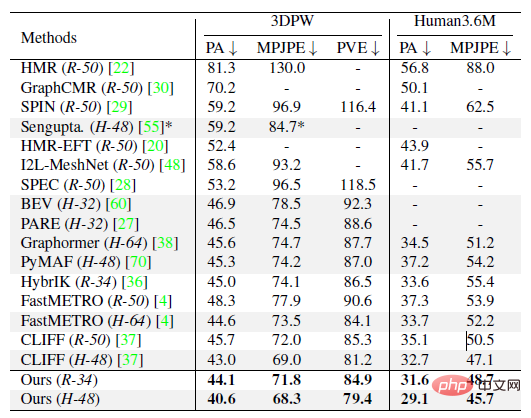
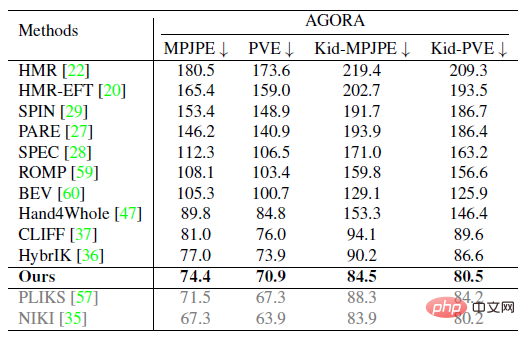
Im experimentellen Teil führte diese Studie einen quantitativen Vergleich mit früheren Methoden an den öffentlichen Datensätzen Human3.6M, 3DPW, AGORA und TotalCapture durch. Es ist ersichtlich, dass die Methode dieser Studie viele frühere Methoden übertrifft. Die letzten beiden grauen Zeilen in der Tabelle unten rechts stammen aus der gleichen Zeit und werden hier der Vollständigkeit halber aufgeführt.

Die folgende Abbildung zeigt einen qualitativen Vergleich mit den bestehenden SOTA-Methoden HybrIK, PARE und CLIFF. Es ist ersichtlich, dass ProPose in einigen Okklusionssituationen bessere Ergebnisse erzielen kann.

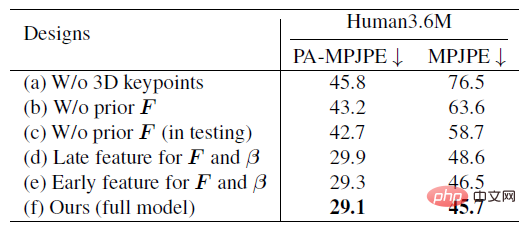
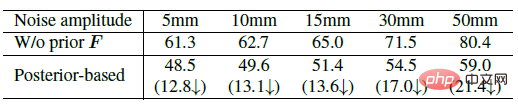
Die folgende Tabelle zeigt eine Reihe von Ablationsexperimenten, die hauptsächlich die Genauigkeit und Robustheit von ProPose demonstrieren. Zu den Benchmark-Methoden gehören die Nichtverwendung dreidimensionaler Schlüsselpunkte, die Nichtverwendung von Priors, die Nichtverwendung von Priors während des Tests, die Auswahl von Features an verschiedenen Standorten im Backbone-Netzwerk usw. Die Tabelle links unten bestätigt vollständig, dass die vorgeschlagene Posterior-Wahrscheinlichkeitsverteilung höher ist Genauigkeit. Die Tabelle rechts unten zeigt den Vergleich der Robustheit gegenüber Rauschen zwischen der Posterior-Methode und der deterministischen IK-Methode. Es ist ersichtlich, dass die Posterior-Methode der Störung durch Rauschen besser standhalten kann.

Zusätzlich zur oben genannten HMR-Aufgabe wurde in dieser Studie auch die Multisensor-Fusion-Aufgabe bewertet. Die Auswirkung einer Einzelansicht und IMUs-Fusion ist unten angegeben.

Das obige ist der detaillierte Inhalt vonDie Effizienz der Animationsproduktion wurde um 80 % gesteigert! Diese KI-Software realisiert hochpräzise Video-Bewegungserfassung mit einem Klick. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!