Timing-Analyse Pentagon-Krieger! Die Tsinghua-Universität schlägt TimesNet vor: führend in der Vorhersage, Füllung, Klassifizierung und Erkennung

Das Erreichen der Aufgabenuniversalität ist ein Kernthema bei der Erforschung grundlegender Deep-Learning-Modelle und auch eines der Hauptanliegen in der jüngsten Richtung großer Modelle.

Allerdings gibt es im Zeitreihenbereich verschiedene Arten von Analyseaufgaben, die eine feinkörnige Modellierung und semantische Informationen auf hoher Ebene erfordern Klassifizierungsaufgaben. So erstellen Sie ein einheitliches, tiefes Grundmodell, um verschiedene Timing-Analyseaufgaben effizient durchzuführen.Es gab bisher keinen etablierten Plan.

Zu diesem Zweck führte ein Team der School of Software der Tsinghua-Universität Untersuchungen zum grundlegenden Problem der Modellierung von Zeitänderungen durch und schlug TimesNet vor, ein grundlegendes aufgabenübergreifendes Timing Das Papier wurde vom ICLR 2023 angenommen.

Autorenliste: Wu Haixu*, Hu Tenge* , Liu雍*, Zhou Hang, Wang Jianmin, Long Mingsheng

Link: https://openreview.net/pdf?id =ju_Uqw384Oq#🎜 🎜#

Code: https://github.com/thuml/TimesNet#🎜🎜 ##🎜🎜 #

Zeitreihenalgorithmus-Bibliothek: https://github.com/thuml/Time-Series-Library

# 🎜🎜#TimesNet at It hat eine umfassende Führungsrolle bei den fünf Hauptaufgaben der langfristigen und kurzfristigen Vorhersage, dem Auffüllen fehlender Werte, der Erkennung von Anomalien und der Klassifizierung übernommen.

1 Problemanalyse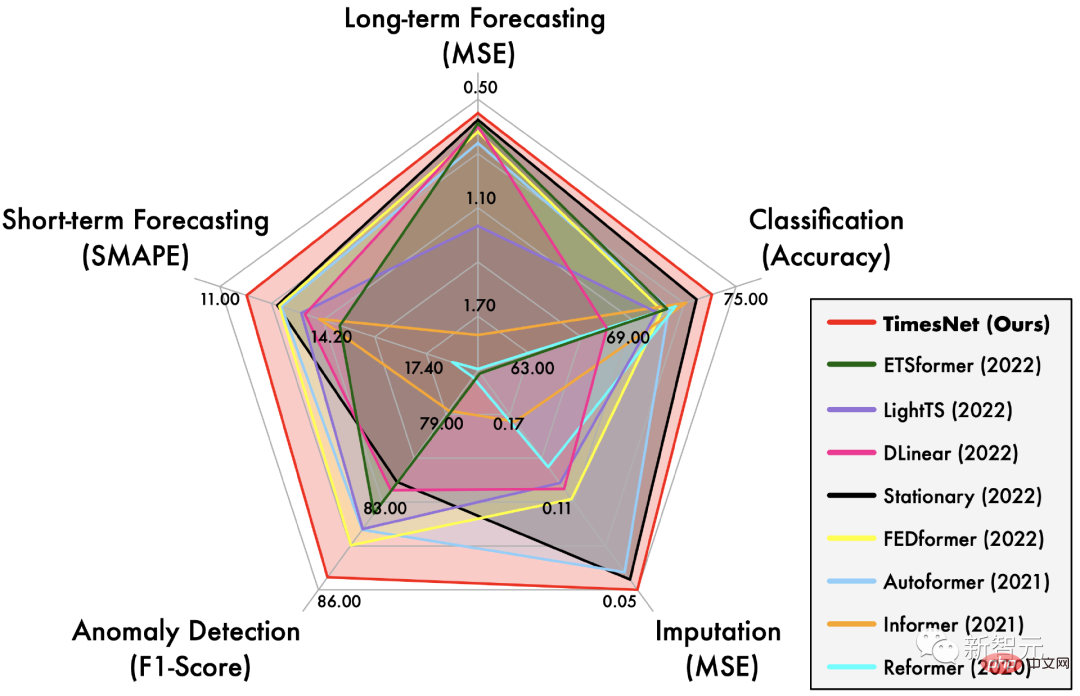

Anders als die Natur Bei Sequenzdaten wie Sprache und Video werden nur einige Skalare zu einem bestimmten Zeitpunkt in der Zeitreihe gespeichert, und weitere wichtige Informationen sind in der zeitlichen Variation (zeitliche Variation) enthalten.

Daher Die Modellierung von Timing-Änderungen ist ein gemeinsames Kernthema für alle Arten von Timing-Analyseaufgaben.

In den letzten Jahren wurden verschiedene Tiefenmodelle häufig in Timing-Analyseaufgaben eingesetzt, wie z. B. rekurrente neuronale Netze (RNN) und zeitliche Faltungsnetze (TCN). ) und Transformatornetzwerk (Transformer).

Die ersten beiden Arten von Methoden konzentrieren sich jedoch hauptsächlich auf die Erfassung von Änderungen zwischen nahegelegenen Momenten und verfügen über unzureichende Modellierungsmöglichkeiten für langfristige Abhängigkeiten.

Obwohl Transformer einen natürlichen Vorteil bei der Modellierung langfristiger Abhängigkeiten hat, ist es aufgrund der äußerst komplexen zeitlichen Änderungen in der realen Welt nur auf die Aufmerksamkeit zwischen diskreten Zeitpunkten angewiesen (Achtung) Es ist schwierig, zuverlässige Timing-Abhängigkeiten zu ermitteln.

Zu diesem Zweck analysiert dieser Artikel Timing-Änderungen aus einer neuen Multiperiodizitätsperspektive, wie in der folgenden Abbildung dargestellt. Wir beobachten, dass:

Zeitreihen sind von Natur aus

• mehrperiodisch #🎜🎜 #. Zeitreihendaten in der realen Welt sind oft die Überlagerung verschiedener periodischer Prozesse, beispielsweise ändern sich Verkehrsdaten kurzfristig , während sich langfristig wöchentlich ändert. Diese Daten verschiedener Zeiträume überlappen und stören sich gegenseitig, was die Zeitreihenanalyse vor große Herausforderungen stellt.

Zeitreihendarstellung

Zwei zeitliche Änderungen innerhalb des Zyklus und zwischen den Zyklen
• # 🎜 🎜#. Insbesondere für den Prozess eines bestimmten Zyklus bezieht sich die Änderung zu jedem Zeitpunkt nicht nur auf den angrenzenden Moment, sondern auch auf ähnliche Prozesse im angrenzenden Zyklus Sehr relevant. Dabei entsprechen Veränderungen innerhalb eines Zyklus kurzfristigen Prozessen, während Veränderungen zwischen einem Zyklus langfristige Trends in aufeinanderfolgenden Zyklen widerspiegeln können. Hinweis: Wenn die Zeitreihe keine offensichtliche Periodizität aufweist, entspricht dies einer Situation, in der die Periode unendlich lang ist.
2 Design-Ideen

Basierend auf den beiden oben genannten Beobachtungen haben wir die Struktur von TimesNet wie folgt entworfen: #🎜 🎜 #Die

• Multiperiodizität von Zeitreihen inspirierte natürlich eine modulare Designidee, das heißt, ein Modul erfasst die Zeitreihenänderungen, die von einem bestimmten Zeitraum dominiert werden. Diese modulare Designidee kann komplexe Zeitänderungen entkoppeln, was für die spätere Modellierung von Vorteil ist. Für die
• Änderungen innerhalb und zwischen Zyklen von Zeitreihen schlägt dieser Artikel auf innovative Weise vor, eindimensionale Zeitreihendaten zur Analyse auf einen zweidimensionalen Raum zu erweitern. Wie in der Abbildung oben gezeigt, können durch Falten einer eindimensionalen Zeitreihe basierend auf mehreren Zyklen mehrere zweidimensionale Tensoren (2D-Tensoren) erhalten werden. Die Spalten und Zeilen jedes zweidimensionalen Tensors spiegeln die Zeitreihe innerhalb des Zyklus wider und zwischen den Zyklen Änderungen, das heißt, wir erhalten Zeitliche 2D-Variationen.

Das obige Beispiel zeigt den Visualisierungseffekt der Faltung eindimensionaler Zeitreihendaten in einen zweidimensionalen Raum. Hier spiegelt die Periodenrichtung Änderungen innerhalb des Zyklus wider, während die Frequenzrichtung Änderungen zwischen den Zyklen darstellt. Wir können sehen, dass die in den zweidimensionalen Raum umgewandelten Zeitreihendaten eine offensichtliche zweidimensionale Lokalität (2D-Lokalität) aufweisen.

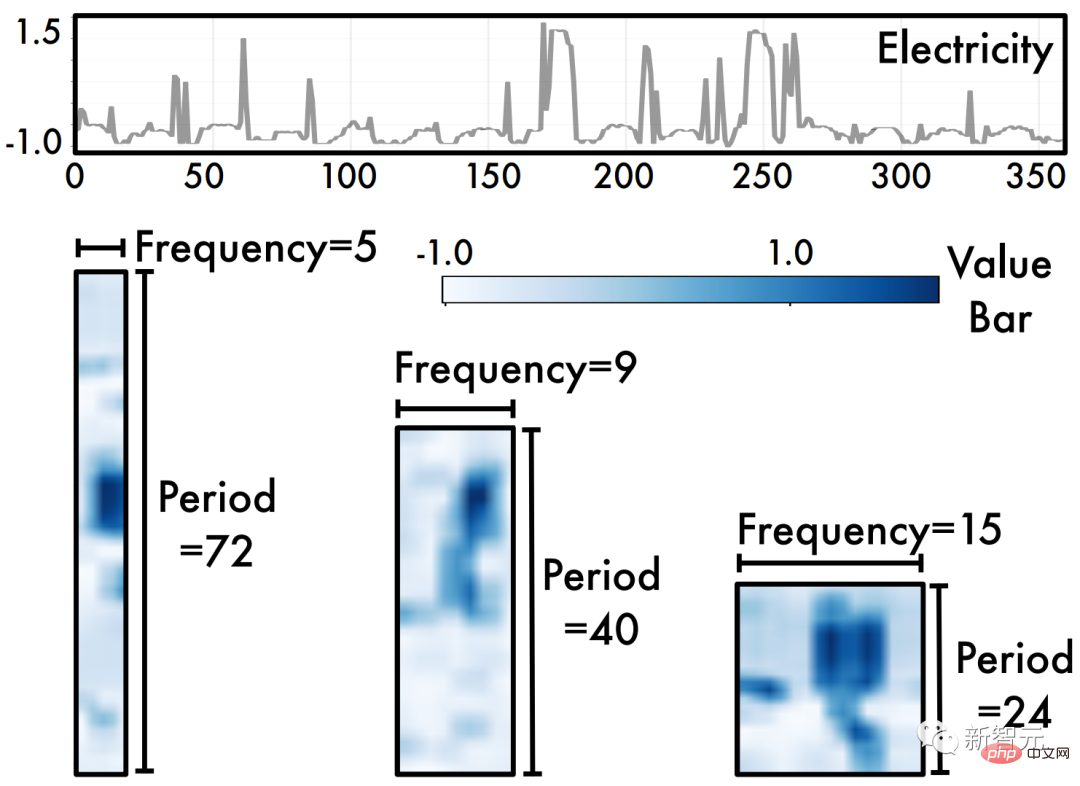
Daher können wir nach dem Falten der Zeitreihendaten direkt das erweiterte

Visual Backbone Network

verwenden, um eine Merkmalsextraktion der Zeitreihendaten durchzuführen, wie z. B. Swin Transformer, ResNeXt, ConvNeXt usw. Dieses Design ermöglicht es auch, Timing-Analyseaufgaben direkt vom boomenden Computer-Vision-Bereich zu profitieren. 3 TimesNet

Basierend auf den oben genannten Ideen haben wir das TimesNet-Modell vorgeschlagen, das komplexe Zeitreihenänderungen durch eine modulare Struktur in verschiedene Zyklen zerlegt und eine zyklusinterne und einheitliche Modellierung der Variation von Woche zu Woche realisiert

.

In diesem Abschnitt stellen wir zunächst die Methode zur Erweiterung von Zeitreihendaten auf den zweidimensionalen Raum vor und stellen dann die Gesamtarchitektur des Modells vor. 3.1 Timing-Änderungen: 1D->2D

Für eine eindimensionale Zeitreihe mit einer Zeitlänge von und einer Kanaldimension von können die Periodeninformationen direkt durch die schnelle Fourier-Transformation (FFT) der Zeitdimension extrahiert werden, das heißt:

wobei, die Intensität jeder Frequenzkomponente in darstellt, wobei die Frequenz mit der größten Intensität der signifikantesten Periodenlänge entspricht.

(2) Sequenzfaltung 1D->2D

Für ausgewählte Zeiträume wird die ursprüngliche eindimensionale Zeitreihe entsprechend gefaltet:

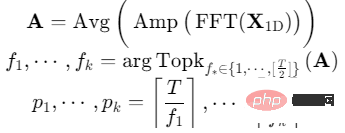
Unter anderem macht das Auffüllen von 0 am Ende der Sequenz die Sequenzlänge teilbar.

Durch die obigen Operationen erhalten wir einen Satz zweidimensionaler Tensoren, die zweidimensionalen Zeitreihenänderungen mit einer Periode von entsprechen. 3.2 Modelldesign

Die Gesamtarchitektur von TimesNet ist in der Abbildung dargestellt:

Insgesamt besteht TimesNet aus gestapelten TimesBlocks. Die Eingabesequenz durchläuft zunächst die Einbettungsschicht, um tiefe Merkmale zu erhalten. Für den TimesBlock der dritten Schicht lautet seine Eingabe und seine Ausgabe:

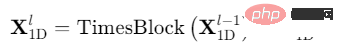
Konkret enthält jeder TimesBlock, wie in der folgenden Abbildung dargestellt, die folgenden Unterprozesse:

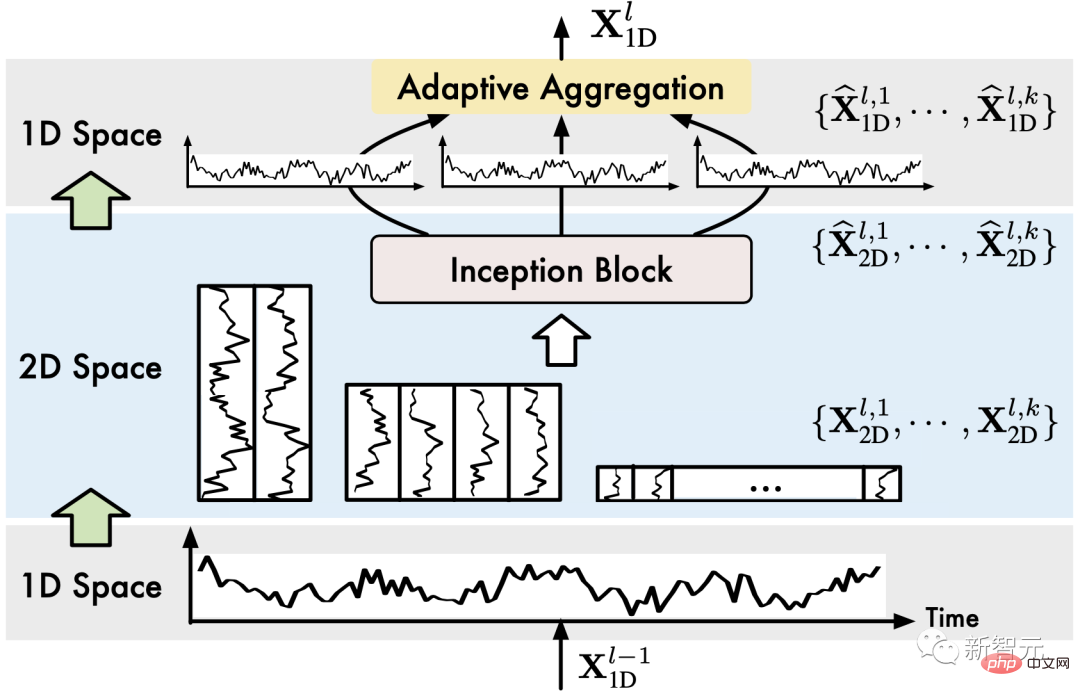
(1) Faltende Zeitreihe (1D->2D) : TimesBlock Zuerst extrahieren die eingegebenen eindimensionalen Zeitreihenfunktionen den Zyklus und konvertieren ihn dann in zweidimensionale Zeitreihenänderungen, was im vorherigen Abschnitt behandelt wurde:

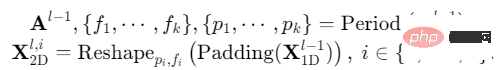
(2) Zweidimensional extrahieren Zeitreihenänderungsdarstellung (2D-Darstellung) : Wie zuvor analysiert, weisen die konvertierten zweidimensionalen Zeitreihenänderungen eine 2D-Lokalität auf, sodass die 2D-Faltung direkt zum Extrahieren von Merkmalen verwendet werden kann. Hier haben wir uns für das klassische Inception-Modell entschieden, nämlich:

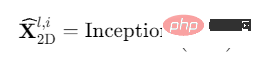
Da wir 1D-Zeitmerkmale in 2D-Raum konvertiert haben, ist es erwähnenswert, dass wir auch viele hochmoderne Modelle im Computerbereich nutzen können Vision, zum Beispiel ResNeXt, ConvNeXt, Attention-based Swin Transformer usw. Dadurch kann die Zeitreihenanalyse Hand in Hand mit dem visuellen Backbone-Netzwerk arbeiten. ⋅ Entfernen Sie die 0, die durch die Padding(⋅)-Operation in Schritt (1) hinzugefügt wurde.

(4) Adaptive Fusion (1D-Aggregation): Um mehrperiodige Informationen zu fusionieren, führen wir eine gewichtete Summierung der extrahierten zweidimensionalen Zeitreihendarstellungen durch und das ausgewählte Summationsgewicht wird in Schritt ( 1) Die entsprechende Frequenzintensität:

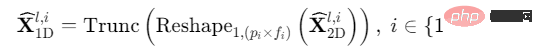
Durch die Konvertierung von 1D-Zeitreihen in ein 2D-Raumdesign realisiert TimesNet die Zeitreihenänderungskonstruktion „mehrerer Perioden, um zweidimensionale Zeitreihenänderungen separat zu extrahieren und dann Führen Sie den Formprozess „Adaptive Fusion“ durch.

4 Experimente

Wir führten Experimente zu fünf Hauptaufgaben durch: Langzeitvorhersage, Kurzzeitvorhersage, Füllen fehlender Werte, Anomalieerkennung und Klassifizierung, wobei wir 36 Datensätze und 81 verschiedene experimentelle Einstellungen abdeckten.

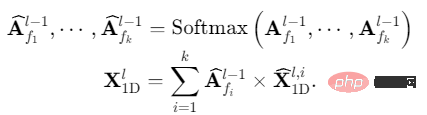
Gleichzeitig wurden 19 verschiedene Tiefenmethoden verglichen, darunter die neuesten Modelle auf Basis von RNN, CNN, MLP und Transformer, wie N-BEATS (2019), Autoformer (2021), LSSL (2022), N-Hits (2022), FEDformer (2022), Dlinear (2023) usw.

4.1 Gesamtergebnisse

Wie im ersten Radardiagramm gezeigt, hat TimesNet bei allen fünf Aufgaben SOTA erreicht.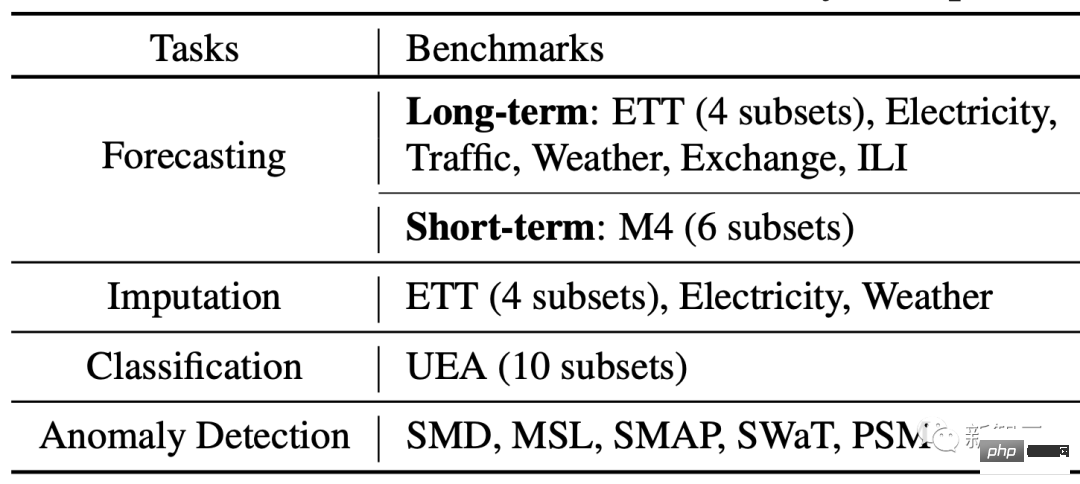

(1) Langfristige Vorhersage: Bei dieser hochkarätigen Aufgabe übertrifft TimesNet die neuesten Transformer- und MLP-basierten Modelle.

(2) Kurzfristige Vorhersage: Der in diesem Experiment verwendete M4-Datensatz enthält 6 Unterdatensätze mit unterschiedlichen Abtastfrequenzen mit insgesamt mehr als 100.000 Daten. TimesNet erzielte in dieser komplexen Datenverteilungssituation immer noch optimale Ergebnisse und bestätigte die Modellierungsfähigkeiten des Modells für zeitliche Änderungen.

(3) Klassifizierungsaufgabe : Bei dieser Aufgabe hat TimesNet den klassischen Rocket-Algorithmus und das hochmoderne Deep-Learning-Modell Flowformer übertroffen.

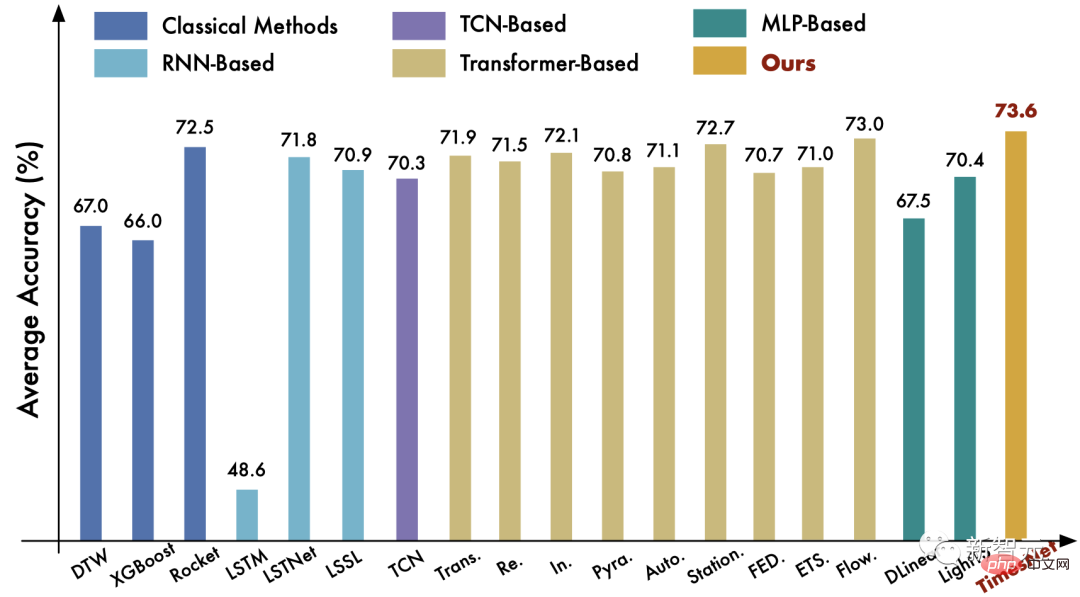
Weitere Aufgabenvergleiche finden Sie im Papier.

4.2 Verallgemeinerung des visuellen Backbone-Netzwerks

Wir ersetzen das Inception-Netzwerk in TimesNet durch verschiedene visuelle Backbone-Netzwerke wie ResNet, ConvNext, Swin Transformer usw.

Wie in der Abbildung unten gezeigt, kann ein fortschrittlicheres visuelles Backbone-Netzwerk bessere Ergebnisse bringen. Dies bedeutet auch, dass die Zeitreihenanalyse im Rahmen von TimesNet direkt von Fortschritten im Bereich der visuellen Backbone-Netzwerke profitieren kann.

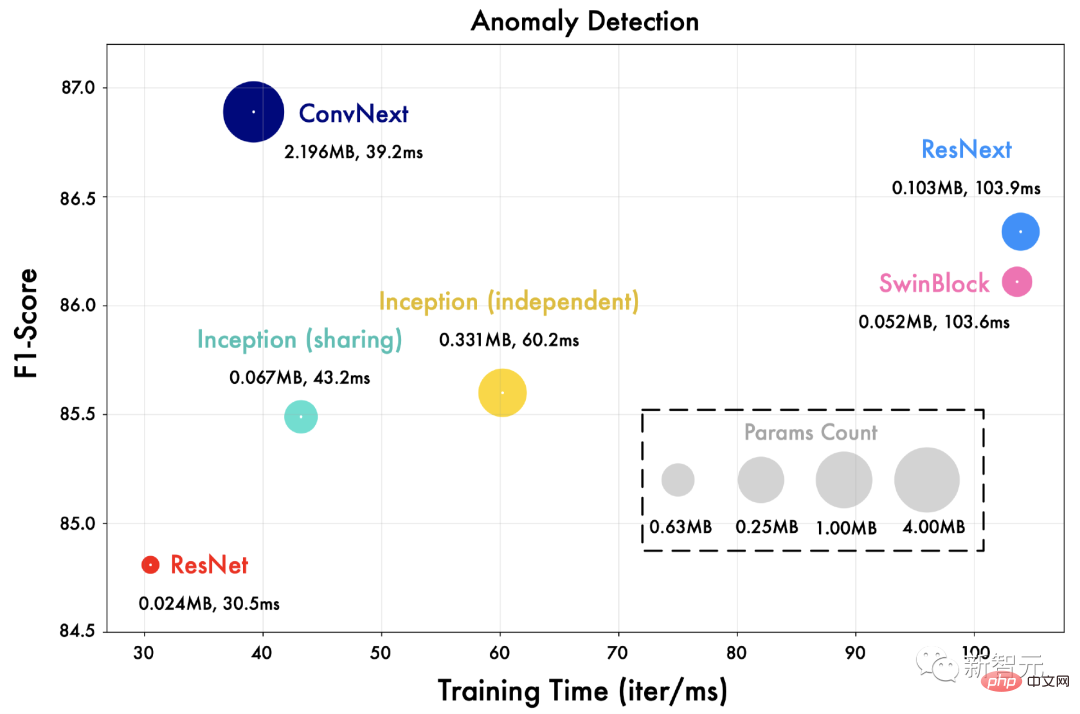
4.3 Darstellungsanalyse

Um die Quelle des TimesNet-Effekts weiter zu untersuchen, zeigen wir die Beziehung zwischen „CKA-Ähnlichkeit zwischen der unteren Schicht des Modells und der Darstellung der oberen Schicht“ und „Modelleffekt“. Je geringer die CKA-Ähnlichkeit ist, desto größer ist der Darstellungsunterschied zwischen der unteren und der oberen Schicht des Modells, dh die Darstellung ist hierarchischer.

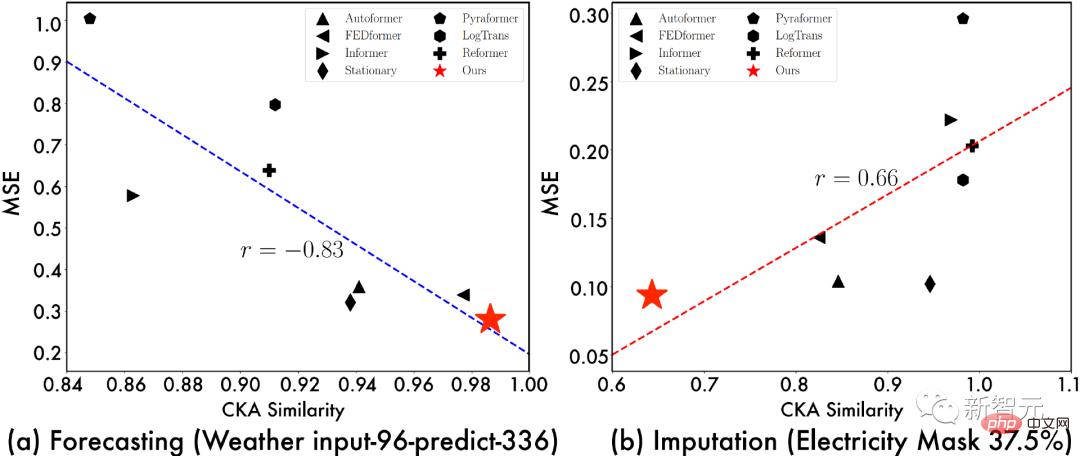
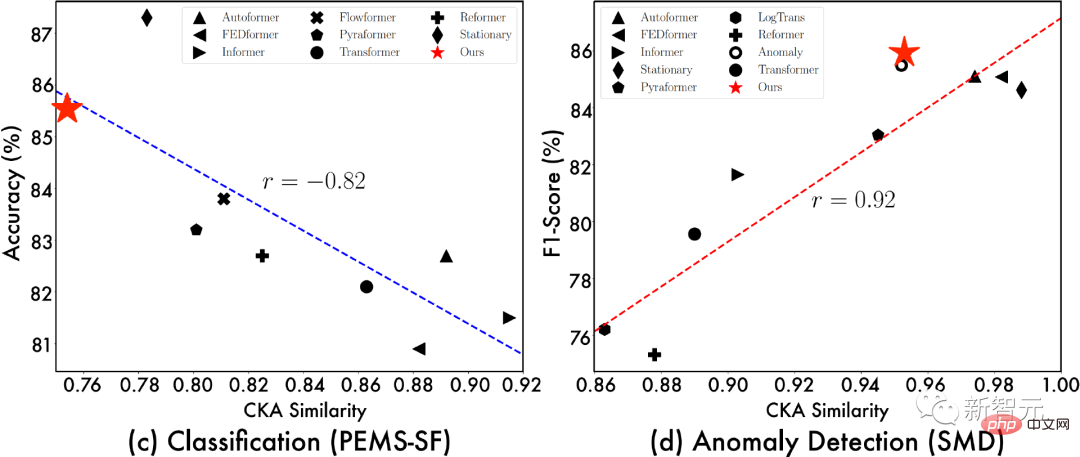
Aus der obigen Visualisierung können wir Folgendes beobachten:

• Bei Vorhersage- und Anomalieerkennungsaufgaben neigen Modelle mit besserer Leistung dazu, eine Darstellungsähnlichkeit von unten nach oben zu haben Je höher , es zeigt an, dass die Aufgabe Darstellungen auf niedrigerer Ebene erfordert;
• Je besser das Modell ist, desto geringer ist die Darstellungsähnlichkeit zwischen der unteren und der oberen Ebene , was darauf hinweist, dass diese Aufgabe hierarchisch ist Darstellung, d. h. bessere globale Funktionen zur Merkmalsextraktion.

Dank der Faltungsoperation im 2D-Raum kann TimesNet geeignete Darstellungen für verschiedene Aufgaben lernen. Beispielsweise lernt es bei Vorhersage- und Anomalieerkennungsaufgaben Darstellungen auf niedriger Ebene bei Klassifizierungs- und Füllaufgaben lernt hierarchische abstrakte Merkmale. Dies beweist weiter die Aufgabenverallgemeinerung von TimesNet als Grundmodell.

Gleichzeitig liefert die obige Darstellungsanalyse auch Entwurfsideen für tiefe Modelle für bestimmte Aufgaben. Beispielsweise müssen wir uns bei Vorhersageaufgaben auf die Extraktion zugrunde liegender feinkörniger Merkmale konzentrieren und bei Füllaufgaben. Wir müssen das Lernen globaler Darstellungen weiter berücksichtigen.

5 Zusammenfassung

Inspiriert von der mehrperiodischen Natur von Zeitreihen schlägt dieser Artikel ein Grundmodell für die Zeitreihenanalyse vor, das universell für Aufgaben geeignet ist – TimesNet. Dieses Modell faltet eindimensionale Zeitreihen auf innovative Weise in einen zweidimensionalen Raum und verwendet die 2D-Faltung, um Zeitreihenmerkmale zu erhalten. Durch diese Innovation können Timing-Analyseaufgaben direkt vom boomenden visuellen Backbone-Netzwerk profitieren, was für die nachfolgende Forschung sehr inspirierend ist.

Gleichzeitig hat TimesNet eine umfassende Führungsrolle bei den fünf gängigen Zeitreihenanalyseaufgaben Langzeit- und Kurzzeitvorhersage, Füllen fehlender Werte, Anomalieerkennung und Klassifizierung übernommen und verfügt über einen hervorragenden Anwendungswert.

Das obige ist der detaillierte Inhalt vonTiming-Analyse Pentagon-Krieger! Die Tsinghua-Universität schlägt TimesNet vor: führend in der Vorhersage, Füllung, Klassifizierung und Erkennung. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!