Heim >Technologie-Peripheriegeräte >KI >KI kann 82 % der Probleme in mathematischen Datenbanken nachweisen. Das neue SOTA wurde erreicht und basiert immer noch auf Transformer.
KI kann 82 % der Probleme in mathematischen Datenbanken nachweisen. Das neue SOTA wurde erreicht und basiert immer noch auf Transformer.
- 王林nach vorne
- 2023-04-10 08:51:08893Durchsuche

Ich muss sagen, dass Wissenschaftler in letzter Zeit besessen davon sind, KI-Matheunterricht zu geben.
Nein, auch das Facebook-Team machte mit und schlug ein neues Modell vor, das die Demonstration von Theoremen vollständig automatisieren kann und deutlich besser als SOTA ist.
Sie müssen wissen, dass es mit zunehmender Komplexität mathematischer Theoreme immer schwieriger wird, die Theoreme allein durch menschliche Kraft zu beweisen.
Daher ist der Einsatz von Computern zur Demonstration mathematischer Theoreme zu einem Forschungsschwerpunkt geworden.
OpenAI hat zuvor auch ein auf diese Richtung spezialisiertes Modell GPT-f vorgeschlagen, das 56 % der Probleme in Metamath demonstrieren kann.
Die neueste, dieses Mal vorgeschlagene Methode kann diese Zahl auf 82,6 % erhöhen.
Gleichzeitig sagen Forscher, dass diese Methode weniger Zeit in Anspruch nimmt und den Rechenverbrauch im Vergleich zu GPT-f auf ein Zehntel des Originals reduzieren kann.
Könnte man sagen, dass die KI diesmal im Kampf mit der Mathematik erfolgreich sein wird
Oder Transformer
Die in diesem Artikel vorgeschlagene Methode ist ein Online-Trainingsprogramm, das auf Transformer basiert.
kann grob in drei Schritte unterteilt werden:
Erstens: Vortraining in der mathematischen Beweisbibliothek;
Zweitens: Feinabstimmung des Richtlinienmodells am überwachten Datensatz; Trainingsstrategiemodell und Beurteilungsmodell. Konkret wird ein Suchalgorithmus verwendet, um das Modell aus der vorhandenen mathematischen Beweisbibliothek lernen zu lassen und es dann weiterzuentwickeln, um weitere Probleme zu beweisen.
Es gibt drei Arten von mathematischen Beweisbibliotheken, nämlich Metamath, Lean und eine selbst entwickelte Beweisumgebung. Um es einfach auszudrücken: Diese Beweisbibliotheken konvertieren gewöhnliche mathematische Sprache in eine Form, die einer Programmiersprache ähnelt.
Metamaths Hauptbibliothek ist set.mm, die etwa 38.000 Beweise basierend auf der ZFC-Mengentheorie enthält. Lean ist besser bekannt als der KI-Algorithmus von Microsoft, der an IMO-Wettbewerben teilnehmen kann. Die Lean-Bibliothek soll dem gleichnamigen Algorithmus alle Mathematikkenntnisse im Grundstudium vermitteln und ihn erlernen, diese Theoreme zu beweisen.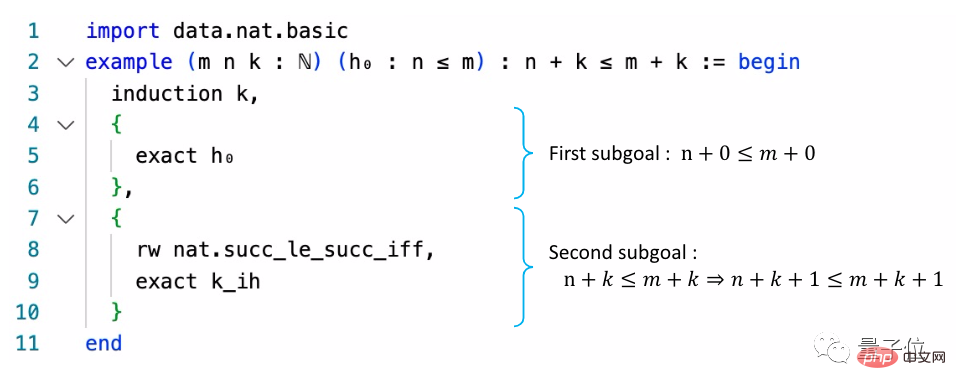 Das Hauptziel dieser Forschung besteht darin, einen Beweiser zu entwickeln, der automatisch eine Reihe geeigneter Strategien zum Beweisen von Problemen generieren kann.
Das Hauptziel dieser Forschung besteht darin, einen Beweiser zu entwickeln, der automatisch eine Reihe geeigneter Strategien zum Beweisen von Problemen generieren kann.
Zu diesem Zweck schlugen die Forscher einen auf MCTS basierenden Nichtgleichgewichts-Hypergraph-Proof-Suchalgorithmus vor.
MCTS wird als Monte-Carlo-Baumsuche übersetzt und wird häufig zur Lösung von Spielbaumproblemen verwendet. Es ist aufgrund von AlphaGo bekannt.
Sein Betriebsprozess besteht darin, durch zufällige Stichproben im Suchraum vielversprechende Aktionen zu finden und dann den Suchbaum basierend auf dieser Aktion zu erweitern.
Die in dieser Studie übernommene Idee ähnelt dieser.
Der Suchnachweisprozess beginnt beim Ziel g, sucht nach unten nach Methoden und entwickelt sich allmählich zu einem Hypergraphen.
Wenn unter einem Zweig eine leere Menge erscheint, bedeutet dies, dass ein optimaler Beweis gefunden wurde.
Zeichnen Sie abschließend während des Backpropagation-Prozesses die Knotenwerte und die Gesamtzahl der Operationen des Superbaums auf.
In diesem Link gingen die Forscher von einem Strategiemodell und einem Beurteilungsmodell aus. Das Richtlinienmodell ermöglicht Stichproben durch das Beurteilungsmodell, mit dem die Fähigkeit der aktuellen Strategie, Beweismethoden zu finden, bewertet werden kann.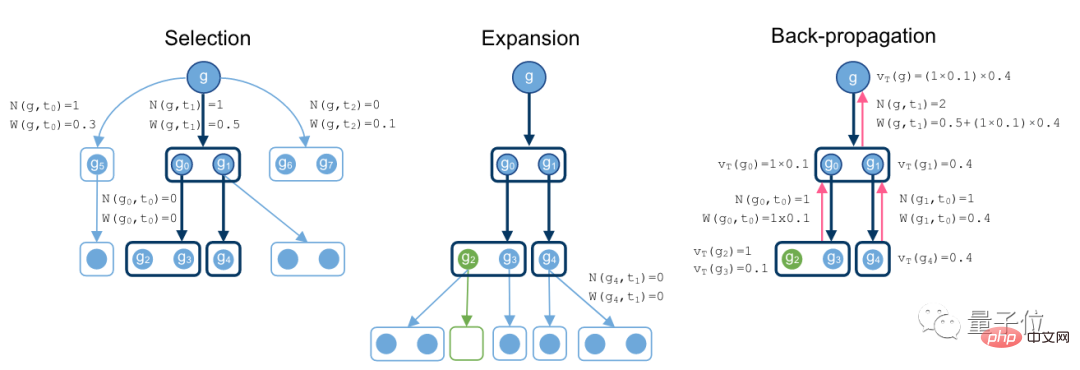 Der gesamte Suchalgorithmus basiert auf den beiden oben genannten Modellen als Referenz.
Der gesamte Suchalgorithmus basiert auf den beiden oben genannten Modellen als Referenz.
Diese beiden Modelle sind Transformer-Modelle und haben das gleiche Gewicht.
Als nächstes kommt die Online-Trainingsphase.
In diesem Prozess sendet der Controller die Abrechnung an die asynchrone HTPS-Verifizierung und sammelt Trainings- und Nachweisdaten.
Der Validator sendet dann die Trainingsbeispiele an den verteilten Trainer und synchronisiert regelmäßig seine Kopie des Modells.
Experimentelle ErgebnisseIn der Testsitzung verglichen die Forscher HTPS mit GPT-f.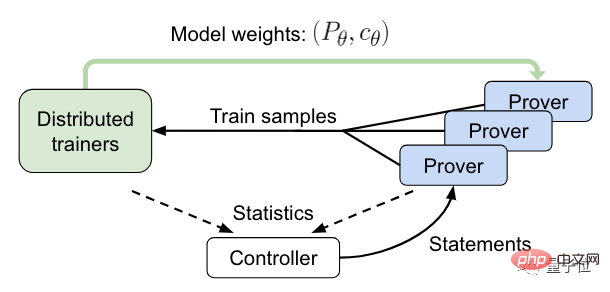 Letzteres ist ein zuvor von OpenAI vorgeschlagenes mathematisches Theorem-Argumentationsmodell, das ebenfalls auf Transformer basiert.
Letzteres ist ein zuvor von OpenAI vorgeschlagenes mathematisches Theorem-Argumentationsmodell, das ebenfalls auf Transformer basiert.
Die Ergebnisse zeigen, dass das Modell nach dem Online-Training 82 % der Probleme in Metamath nachweisen kann und damit den bisherigen Rekord von 56,5 % von GPT-f weit übertrifft.
In der Lean-Bibliothek kann dieses Modell 43 % der Theoreme beweisen, was 38 % mehr als SOTA ist. Im Folgenden sind die IMO-Testfragen aufgeführt, die von diesem Modell bewiesen wurden.

One More Thing
Der Beweis des Vierfarbensatzes mithilfe von Computern zur Demonstration mathematischer Probleme ist eines der bekanntesten Beispiele.
Der Vierfarbensatz ist eines der drei Hauptprobleme der modernen Mathematik. Er besagt, dass „jede Karte nur vier Farben verwenden kann, um Länder mit gemeinsamen Grenzen in verschiedenen Farben einzufärben.“
Da die Demonstration dieses Theorems viele Berechnungen erfordert, konnte niemand es innerhalb von 100 Jahren nach seinem Vorschlag vollständig demonstrieren.
Bis 1976 konnte auf zwei Computern der University of Illinois nach 1.200 Stunden und 10 Milliarden Urteilen endlich nachgewiesen werden, dass jede Karte nur 4 Farben benötigt, um sie zu markieren, was auch in der gesamten Mathematik für Aufsehen sorgte .
Darüber hinaus wird es mit zunehmender Komplexität mathematischer Probleme schwieriger, mit menschlicher Kraft zu überprüfen, ob der Satz korrekt ist.
In letzter Zeit hat sich die KI-Community nach und nach auf mathematische Probleme konzentriert.
Im Jahr 2020 brachte OpenAI das mathematische Theorem-Argumentationsmodell GPT-f auf den Markt, das zur automatischen Theorembeweisung verwendet werden kann.
Diese Methode kann 56,5 % der Beweise im Testsatz abschließen und übertrifft damit das damalige SOTA-Modell MetaGen-IL um mehr als 30 %.
Im selben Jahr veröffentlichte Microsoft auch Lean, das meiner Meinung nach Testfragen stellen kann, was bedeutet, dass KI Fragen stellen kann, die es noch nie zuvor gesehen hat.
Nachdem OpenAI letztes Jahr einen Verifizierer zu GPT-3 hinzugefügt hatte, war der Effekt der Lösung mathematischer Probleme deutlich besser als bei der vorherigen Feinabstimmungsmethode und konnte 90 % des Niveaus von Grundschülern erreichen.
Im Januar dieses Jahres zeigte eine gemeinsame Studie von MIT + Harvard + Columbia University + University of Waterloo, dass das von ihnen vorgeschlagene Modell hohe Mathematikleistungen erbringen kann.
Kurz gesagt, Wissenschaftler arbeiten hart daran, KI, ein Teilfach, sowohl für Künste als auch für Wissenschaften geeignet zu machen.
Das obige ist der detaillierte Inhalt vonKI kann 82 % der Probleme in mathematischen Datenbanken nachweisen. Das neue SOTA wurde erreicht und basiert immer noch auf Transformer.. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Technologietrends, die Sie im Jahr 2023 im Auge behalten sollten
- Wie künstliche Intelligenz Rechenzentrumsteams neue Alltagsaufgaben beschert
- Können künstliche Intelligenz oder Automatisierung das Problem der geringen Energieeffizienz in Gebäuden lösen?
- OpenAI-Mitbegründer im Interview mit Huang Renxun: Die Argumentationsfähigkeiten von GPT-4 haben noch nicht die Erwartungen erfüllt
- Dank der OpenAI-Technologie übertrifft Bing von Microsoft Google im Suchverkehr

