Wie kann man beweisen, dass es sich bei einem Problem um ein VPN-Problem handelt? Informatiker haben einen einfachen Weg gefunden

Das P/NP-Problem ist ein ungelöstes Problem im Bereich der rechnerischen Komplexität. Die Leute haben versucht, die Antwort auf eine Frage zu finden: „Können wir alle Computerprobleme in angemessener Zeit effizient lösen?“

Was ist eine angemessene Zeit? Tatsächlich werden Probleme berücksichtigt, die vor dem Ende des Universums innerhalb einer angemessenen Zeit gelöst werden können. Dennoch scheinen viele Probleme in angemessener Zeit schwer zu lösen zu sein, sodass die Mathematik die Schwierigkeit dieser Probleme nachweisen muss.

Eine Studie aus dem Jahr 2021 beantwortet die obige Frage und bestätigt: Ein großer Teil der Probleme lässt sich nur schwer effektiv lösen.

Paul Beame von der University of Washington kommentierte diese Forschung: „Wie das Besteigen eines Berges ist diese Forschung ein Zwischenstopp auf dem Weg zur computertheoretischen Forschung.“ Die drei Forscher der Forschung: Informatiker Srikanth Srinivasan (links), Nutan Limaye (oben rechts) und Sébastien Tavenas.

In der Studie wurden Probleme betrachtet, bei denen es nur um Addition und Multiplikation ging. Diese Probleme werden jedoch sehr schwierig, wenn sie auf eine bestimmte Lösung beschränkt sind (ein bestimmtes abwechselndes Muster aus Addition und Multiplikation).

Überraschenderweise verwendete die Studie kein neues Framework oder Tool; stattdessen gelang es den Autoren, die von Wigderson, einem Professor an der School of Mathematics am Institute for Advanced Study in Princeton, in Zusammenarbeit mit Noam Nisan beschriebene jahrzehntelange Arbeit zu umgehen der Hebräischen Universität Jerusalem. Einer der Forscher, Srikanth Srinivasan von der Universität Aarhus in Dänemark, sagte: „Wir haben erkannt, dass es einen sehr einfachen Weg gibt, dieses Hindernis zu umgehen. Und wenn eine so einfache Methode verwendet werden kann, um Dinge zu tun, die wir für unmöglich hielten.“ Dann muss es einen besseren Weg geben.

Sie beginnen zu vermuten, dass manche Probleme von Natur aus zu schwer zu lösen sind, egal wie groß oder klein das Problem ist. In Diagrammen besteht beispielsweise ein wichtiges Problem darin, zu bestimmen, ob es einen Hamilton-Pfad gibt, d. h., ob es genau einmal einen Pfad durch jeden Scheitelpunkt gibt. Das Erhöhen der Anzahl der Scheitelpunkte (und Kanten) sollte länger dauern, um festzustellen, ob ein solcher Pfad existiert, aber selbst die besten Algorithmen benötigen mit zunehmender Diagrammgröße exponentiell mehr Zeit, wodurch die Lösung dieses Problems unrealistisch wird.

Informatiker versuchen zu beweisen, dass jeder Algorithmus, der ein schwieriges Problem einer bestimmten Art von Problem auf irgendeine Weise effektiv lösen kann, in eine Lösung für andere ähnlich schwierige Probleme umgewandelt werden kann. Sie nennen diese Art von Problem NP-Problem.

Natürlich gibt es auch viele Probleme, die nicht schwierig erscheinen und deren Lösung nicht allzu viel Zeit in Anspruch nimmt. Viele dieser Probleme sind in gewissem Sinne auch äquivalent, und solche Probleme werden P-Probleme genannt. Sie argumentieren, dass NP-Probleme tatsächlich schwieriger sind als P-Probleme und dass NP-Probleme niemals effizient gelöst werden können. Aber ohne Beweise könnte diese Idee falsch sein.

Daher begannen Informatiker, nach Wegen zu suchen, um zu beweisen, dass NP-Probleme tatsächlich schwieriger sind. Dies erforderte den Nachweis, dass die Lösung von NP-Problemen exponentiell Zeit in Anspruch nehmen muss, aber der Beweis ist nicht einfach.

Wie schwierig ist „schwer“?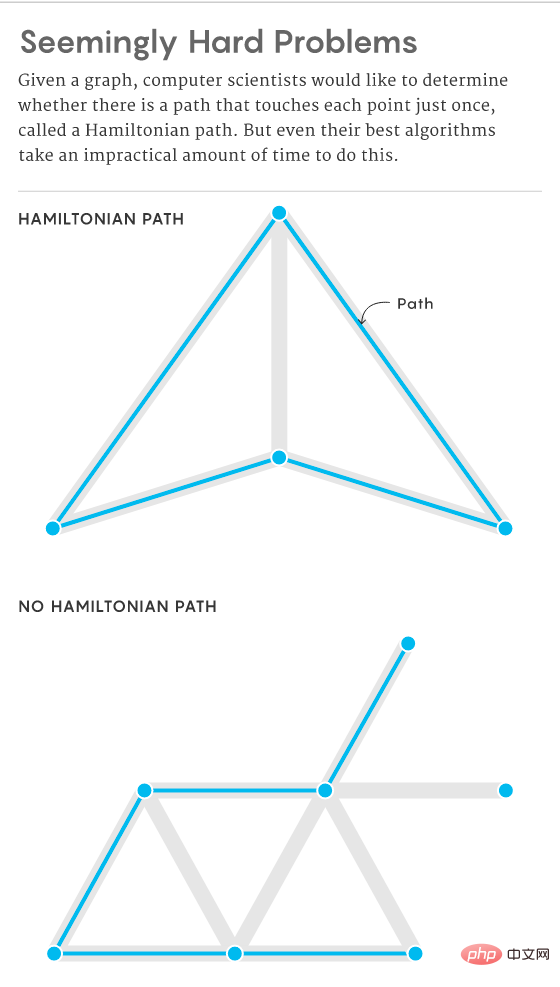

Stellen Sie sich eine Reihe spezifischer Probleme vor, die nur Addition und Multiplikation erfordern. Beispielsweise ist es bei einer gegebenen Menge von Punkten möglich, alle möglichen Hamilton-Pfade (sofern vorhanden) anhand der Daten über die Punkte zu berechnen, und zwar einfach durch Addition und Multiplikation.

Mit zunehmender Problemgröße nehmen einige arithmetische Probleme (z. B. die Berechnung von Hamilton-Pfaden) mehr Zeit in Anspruch. Im Jahr 1979 zeigte Leslie Valiant von der Harvard University, dass viele Rechenaufgaben hinsichtlich des Schwierigkeitsgrads gleichwertig sind, während andere hinsichtlich des Schwierigkeitsgrads gleichwertig sind. Später benannten Informatiker diese beiden Arten von Problemen – VNP bzw. VP – nach ihm.

Und P Wie beim NP-Problem können wir die Schwierigkeit des VNP-Problems nicht beweisen. Wir wissen nur, dass das VNP-Problem schwieriger ist als das NP-Problem. Um beispielsweise einen Pfad zu berechnen, muss zunächst ermittelt werden, ob Der Pfad existiert.

„Es ist schwieriger als NP, daher sollte es einfacher sein zu zeigen, dass es schwierig ist“, sagte Shpilka.

In den folgenden Jahrzehnten machten Informatiker beim VP vs. VNP-Problem viel größere Fortschritte als beim P vs. NP-Problem, aber der größte Teil davon beschränkte sich auf das, was Valiant als sogenannte Unterfelder der algebraischen Komplexität schuf. Vor den jüngsten Arbeiten von Limaye, Srinivasan und Tavenas war es immer noch schwierig zu sagen, ob es Probleme mit der Arithmetik im allgemeinen Sinne gab.

Anpassen von Polynomen

Diese neue Arbeit hilft dabei, die Art und Weise zu erforschen, wie Informatiker über Additions- und Multiplikationsprobleme denken. Mathematisch können diese Probleme als Polynome (z. B. x^2 + 5y + 6) geschrieben werden, die aus addierten und multiplizierten Variablen bestehen.

Für jedes bestimmte Problem, beispielsweise die Berechnung eines Hamilton-Pfades, können Sie ein Polynom konstruieren, das es darstellt. Sie könnten beispielsweise eine Variable verwenden, um jeden Punkt und jede Kante darzustellen, sodass mit dem Hinzufügen weiterer Punkte und Kanten auch mehr Variablen zum Polynom hinzugefügt werden können.

Um zu zeigen, dass ein arithmetisches Problem wie die Berechnung eines Hamilton-Pfades schwierig ist, muss man zeigen, dass die entsprechenden Polynome mehr Operationen erfordern, um in exponentieller Zeit gelöst zu werden, je mehr Punkte und Kanten hinzugefügt werden. Beispielsweise erfordert x^2 eine Operation (x * x), während x^2 + y zwei Operationen erfordert (x * x plus y). Die Anzahl der Operationen wird als Größe des Polynoms bezeichnet.

Aber die Größe des Polynoms ist schwer zu bestimmen. Zum Beispiel das Polynom x^2 + 2x + 1. Es scheint die Größe 4 zu haben (zwei Multiplikationen und zwei Additionen), aber das Polynom kann als Produkt zweier Summen (x + 1)(x + 1) umgeschrieben werden, das weniger Operanden hat – zweimal Addition, eine Multiplikation. Wenn ein Problem größer wird und mehr Variablen zum Polynom hinzugefügt werden, können mathematische Transformationen häufig dazu beitragen, das Polynom zu vereinfachen und zu verkleinern.

Einige Jahre nach Valiants Forschung fanden Informatiker einen Weg, die Größe des Problems einfacher zu analysieren. Zu diesem Zweck schlugen sie eine Eigenschaft namens „Tiefe“ vor, die angibt, wie oft das Polynom zwischen Summen und Produkten wechselt oder wechselt. Beispielsweise hat das Polynom x^2 + 2x + 1 die Tiefe 2, da es die Summe von Produkten ist (z. B. x^2 und 2x). Im Gegensatz dazu hat der Ausdruck (x + 1)(x + 1) eine Tiefe von 3, da er dieselbe Tiefe wie 0 + (x + 1)(x + 1) hat, berechnet als Summe der Produkte.

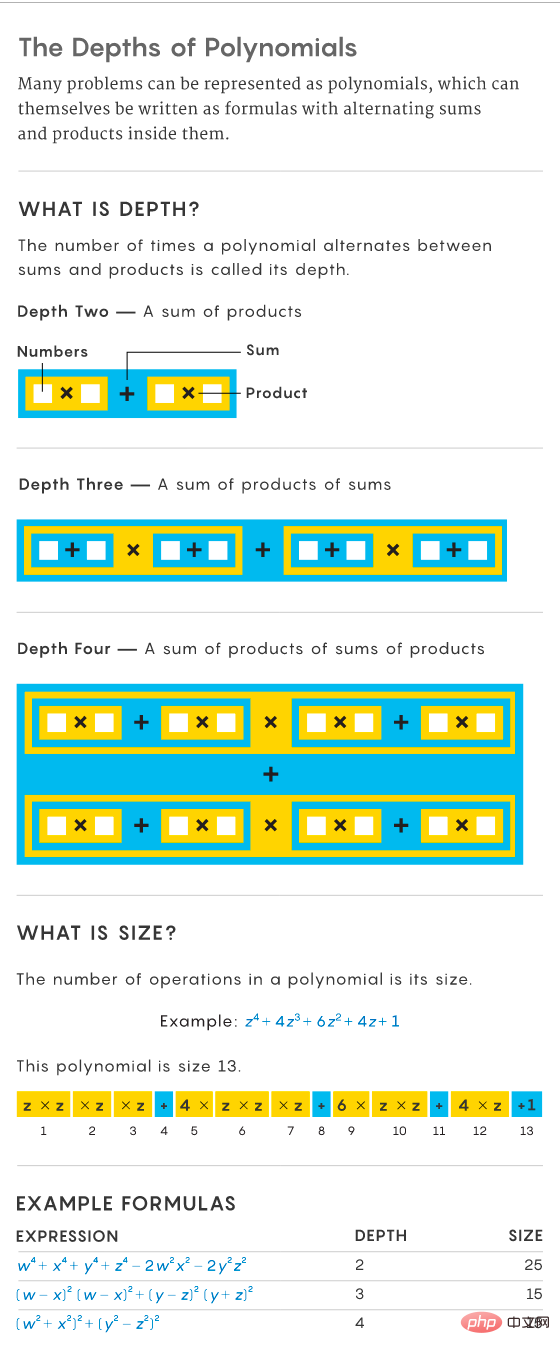
Um Polynome zu vereinfachen, beschränken Informatiker sie auf eine feste Form mit einer Eigenschaft namens „konstante Tiefe“, bei der sich das Muster von Summen und Produkten nicht ändert, wenn das Problem wächst. Dadurch wird ihre Größe fester, da die Größe des Polynoms mit zunehmender Tiefe abnimmt. Ein Ausdruck für eine konstante Tiefe wird Formel genannt. Eine konstante Tiefe ermöglicht größere Fortschritte bei der Untersuchung von Polynomen.

Magische „Tiefe“

1996 konzentrierten sich Nisan und Wigderson auf die Lösung des Problems der Matrixmultiplikation. Sie vereinfachten dieses Problem auf zwei Arten. Zuerst drücken sie es mit der Formel für konstante Tiefe aus – einer Tiefe von 3. Zweitens betrachteten sie nur Formeln mit einer einfachen Struktur, in denen jede Variable einen maximalen Exponenten von 1 hat, was das ursprüngliche Problem zu einem „multilinearen“ Problem macht.

Informatiker haben herausgefunden, dass bestimmte Probleme auf Kosten einer subexponentiellen Vergrößerung der Polynomgröße (vergleichbar mit der Wachstumsrate des exponentiellen Wachstums) in relativ einfache mengenmultilineare Strukturen umgewandelt werden können.

Nisan und Wigderson zeigten später, dass die Lösung des Matrixmultiplikationsproblems mit zunehmender Matrix eine exponentielle Zeit zur Lösung benötigt. Mit anderen Worten: Sie zeigen, dass ein wichtiges Problem schwierig ist, und sie bemühen sich zu zeigen, dass eine Klasse von Problemen schwierig ist. Allerdings gelten ihre Ergebnisse nur für Formulierungen mit einfachen, kollektiven multilinearen Strukturen.

Leslie Valiant

Eine Vergrößerung der Tiefe eines Polynoms führt tendenziell zu einer Verringerung seiner Größe. Im Laufe der Zeit haben Informatiker den Kompromiss zwischen diesen beiden Eigenschaften präziser gestaltet. Sie zeigen, dass multilineare Ensemble-Polynome durch Hinzufügen von zwei Tiefenstufen zur Tiefe 3 den Größengewinn ihrer multilinearen Ensemble-Struktur ausgleichen können. Wenn strukturierte Formeln der Tiefe 5 eine exponentielle Zeit benötigen, gilt dies auch für allgemeine, unstrukturierte Formeln der Tiefe 3.

Neue Arbeiten von Srikanth Srinivasan et al. zeigen, dass tiefe multilineare 5-Satz-Formulierungen von Matrixmultiplikationsproblemen tatsächlich exponentiell wachsen. Dies bedeutet, dass die allgemeine Tiefenformel 3 ebenfalls exponentielle Zeit benötigt. Anschließend zeigten sie, dass ein ähnliches Muster für alle Tiefen gilt (nicht nur für 3 und 5). Mit dieser Beziehung zeigten sie, dass die Größe einer allgemeinen Formel beliebiger Tiefe für dasselbe Problem exponentiell mit der Größe des Problems zunimmt.

Sie zeigen auch, dass es schwierig ist, die Matrixmultiplikation in einer Formel mit konstanter Tiefe auszudrücken, egal wie tief diese ist.

Die Ergebnisse dieser Studie liefern das erste allgemeine Verständnis dafür, wann eine Rechenaufgabe „schwer“ ist – wenn sie nicht in einer Formel mit konstanter Tiefe ausgedrückt werden kann. Das spezifische Problem der Matrixmultiplikation ist als VP-Problem bekannt. Und es ist bekannt, dass das VP-Problem relativ einfach ist, wenn es nicht auf eine konstante Tiefe beschränkt ist. Es stellt sich also heraus, dass die konstante Tiefe die Ursache für die „Schwierigkeit“ des Problems ist.

Sind VNP-Probleme schwieriger als VP-Probleme? Die neuen Ergebnisse veranschaulichen dies nicht direkt, sie zeigen lediglich, dass die Formel mit konstanter Tiefe schwierig ist. Dies ist jedoch immer noch ein wichtiger Meilenstein beim Beweis, dass das VNP-Problem nicht mit dem VP-Problem gleichwertig sein kann.

Für das größere P vs. NP-Problem können wir jetzt optimistischer sein, dass die Antwort eines Tages gefunden wird. Denn um schwierige Probleme zu lösen, müssen wir zunächst wissen, welche Richtungen aussichtslos sind.

Das obige ist der detaillierte Inhalt vonWie kann man beweisen, dass es sich bei einem Problem um ein VPN-Problem handelt? Informatiker haben einen einfachen Weg gefunden. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!