Heim >Technologie-Peripheriegeräte >KI >Michael Bronstein greift auf die algebraische Topologie zurück und schlägt eine neue Computerstruktur für graphische neuronale Netze vor!
Michael Bronstein greift auf die algebraische Topologie zurück und schlägt eine neue Computerstruktur für graphische neuronale Netze vor!
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2023-04-09 22:11:361514Durchsuche
Dieser Artikel wurde gemeinsam von Cristian Bodnar und Fabrizio Frasca verfasst und von C. Bodnar, F. Frasca und anderen im Jahr 2021 ICML „Weisfeiler and Lehman Go Topological: Information Transfer Simple Network“ und 2021 NeurIPS „Weisfeiler and Lehman Go“ veröffentlicht Mobilfunk: CW-Netzwerk“ 》Die Arbeit dient als Referenz.
Dieser Artikel ist nur ein Teil der Reihe „Graph Neural Network“, die aus den Perspektiven der Differentialgeometrie und der algebraischen Topologie diskutiert wird.
Grafiken können verwendet werden, um alles zu modellieren, von Computernetzwerken bis hin zu Teilcheninteraktionen im Large Hadron Collider. Graphen sind aufgrund ihrer diskreten und kombinatorischen Natur allgegenwärtig, wodurch sie abstrakte Beziehungen ausdrücken und gleichzeitig einfach zu berechnen sind. Einer der Gründe für ihre Beliebtheit besteht darin, dass Diagramme die Geometrie abstrahieren, d. h. wo sich Knoten im Raum befinden oder wie Kanten gekrümmt sind, sodass nur eine Darstellung davon übrig bleibt, wie Knoten verbunden sind.
Die Graphentheorie entstand aus Leonhard Eulers Beobachtung in seinem 1741 erschienenen Buch „Geometria situs“, dass es keine Lösung für das berühmte Königsberger Sieben-Brücken-Problem gab.
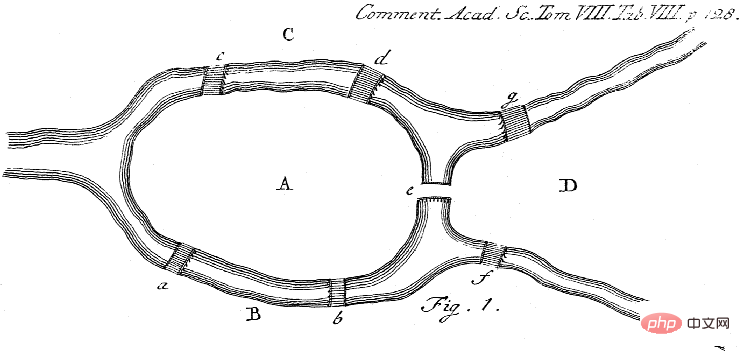
Abbildung: Das Sieben-Brücken-Problem erfordert die Suche nach einer Rundwanderroute in der Stadt Königsberg, ohne die Brücke mehrmals zu überqueren. Wie Euler sagte, kommt es nicht auf die genaue Form der Stadt Königsberg an, sondern darauf, wie die verschiedenen Grundstücke (Knoten der Grafik) miteinander verbunden sind (Kanten). Euler zeigte, dass ein solcher Kreis genau dann existiert, wenn alle Knoten einen geraden Grad haben. Darüber hinaus sind nur fünf der ursprünglichen Brücken bis in die Neuzeit erhalten geblieben. Quelle: Wikipedia
Interessanterweise markierte Eulers Entdeckung nicht nur den Beginn der Graphentheorie, sondern wird oft auch als Geburtsstunde der Topologie angesehen. Wie bei Graphen interessieren sich Topologen für die Eigenschaften eines Raums, die unabhängig von seiner spezifischen Form oder Geometrie sind.
Der moderne Ausdruck dieser Ideen erschien 1895 in „Analysis situs“, einer bahnbrechenden Arbeit von Henri Poincaré, dessen Arbeit das Interesse an der kombinatorischen Beschreibung von Mannigfaltigkeiten weckte. Topologische Invarianten können in diesen Mannigfaltigkeiten leichter gefunden und berechnet werden .
Bildunterschrift: Leonhard Euler (1707-1783) und Henri Poincaré (1854-1912)
Diese kombinatorischen Beschreibungen werden heute Zellkomplexe genannt und können als höhere Dimensionen der Graphenverallgemeinerung betrachtet werden .
Im Gegensatz zu Diagrammen, die aus Knoten und Kanten bestehen, können Zellkomplexe auch höherdimensionale Strukturen oder „Zellen“ enthalten: Scheitelpunkte sind 0-Zellen, Kanten sind 1-Zellen, 2D-Oberflächen sind 2-Zellen usw. Um einen Zellkomplex aufzubauen, können wir ihn schichten, indem wir die Grenzen einer Zelle mit anderen Zellen niedrigerer Dimensionen verkleben.
In besonderen Fällen, wenn die Zellen aus Simplexen bestehen (z. B. Kanten, Dreiecke, Tetraeder usw.), werden diese Räume auch Simplexkomplexe genannt.

Bildunterschrift: Ein Diagramm kann als eine Reihe von Eckpunkten betrachtet werden, an die wir Kanten anhängen (1 Zelle). Ebenso können einzelne Zellkomplexe und Zellkomplexe als Diagramme betrachtet werden, in denen wir 2-Zellen (in Blau dargestellt), 3-Zellen (in Grün dargestellt) usw. verbinden.
1 Topologie im maschinellen Lernen und in der Datenwissenschaft
Wir glauben, dass Menschen nicht 400 Jahre warten müssen, bis die Topologie zu einem praktischen Werkzeug wird.
Topologische Strukturen wie flache Komplexe wurden im maschinellen Lernen und in der Datenwissenschaft unter dem Dach der topologischen Datenanalyse (TDA) verwendet. Diese Art von Methode entstand in den 1990er Jahren in dem Versuch, eine unempfindliche und rauschrobuste Methode zu verwenden um die „Form der Daten“ zu analysieren.
Die Wurzeln von TDA lassen sich auf die Arbeit eines der produktivsten Topologen, Leopold Vietnam Oris, in den späten 1920er Jahren zurückführen. Allerdings mussten diese Technologien bis zum Aufkommen moderner Computer warten, bevor sie in großem Maßstab eingesetzt werden konnten.

Legende: Bei einer gegebenen Punktwolke erzeugt der Schnittpunkt zwischen geschlossenen Kugeln mit festem Radius um jeden Punkt einen einfachen Komplex. Indem wir den Radius der Kugel schrittweise vergrößern, können wir eine verschachtelte Folge einfacher Komplexe erhalten. Bildquelle: Bastian Rieck.
Das Arbeitspferd von TDA ist Persistent Homology (PH), eine Methode zum Extrahieren topologischer Merkmale aus Punktwolken. Ausgehend von einem Datensatz aus Punkten erstellt PH eine verschachtelte Folge einfacher komplexer Zahlen, wobei jede komplexe Zahl einem bestimmten Maßstab der zugrunde liegenden Punktwolke entspricht, die analysiert wird. Anschließend werden verschiedene topologische Merkmale (z. B. verbundene Komponenten, Schleifen oder Löcher) verfolgt, die erscheinen und verschwinden, wenn die Skala allmählich zunimmt und man von einem Komplex in der Sequenz zum nächsten übergeht.
Im Zeitalter des Deep Learning hat die persistente Homologie ein „zweites Leben“ gehabt, da gezeigt wurde, dass man damit Backpropagation durchführen kann, was die Integration bereits etablierter TDA-Geräte in Deep-Learning-Frameworks ermöglicht.
Eine aktuelle Reihe von Arbeiten schlägt verschiedene Verwendungsmöglichkeiten von Vereinfachungen und Zellkomplexen im geometrischen Deep Learning vor, als einen umfassenderen zugrunde liegenden topologischen Raum zur Unterstützung der darauf durchgeführten Daten und Berechnungen.
Einige der frühesten Arbeiten zur Nutzung dieser Perspektive schlugen Faltungsmodelle und Random-Walk-Methoden für die Bearbeitung vereinfachter Komplexe vor. Wie in diesem Artikel können Faltungsmodelle als einfache und konkrete Beispiele für die Informationsübertragung auf Zellkomplexen verstanden werden.
Da die Berechnung von der topologischen Struktur dieser Räume (dh der Nachbarschaftsstruktur) abhängt, nennen wir diese Methode topologische Informationsübertragung. In diesem Rahmen tauschen benachbarte Einheiten, möglicherweise unterschiedlicher Größe, Informationen aus, wie in der Abbildung unten dargestellt.
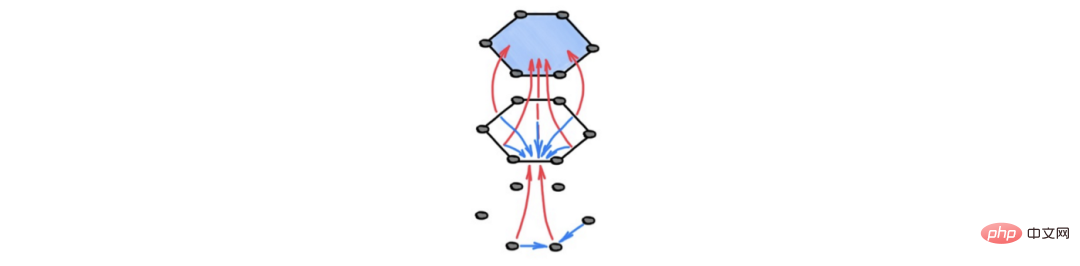
Bildunterschrift: Schematische Darstellung der topologischen Informationsübertragung. Die blauen Pfeile beschreiben die „horizontale“ Informationsausbreitung zwischen benachbarten Zellen in der oberen Schicht, d. h. Zellen an den Grenzen derselben hochdimensionalen Zelle. Der rote Pfeil stellt die „vertikale“ Informationsausbreitung dar, bei der eine Zelle an ihren Rändern Informationen von niedrigerdimensionalen Zellen empfängt. Diese Berechnung kann als (differenzierbare) Ensembleform interpretiert werden, indem Informationen aus Grenzzellen in einer gröberen Darstellung zusammengefasst werden.
Jenseits von Graphen in GNNs
Trotz der reichhaltigen Struktur, die zelluläre Komplexe bieten, können wir nicht ignorieren, dass Graphen bei weitem die häufigsten topologischen Objekte beim maschinellen Lernen sind und nur wenige Datensätze diese übertreffen. Dennoch kann man diese interessanten topologischen Räume durch Transformation des Eingabegraphen nutzen.
Wir nennen die Umwandlung eines Graphen in einen hochdimensionalen topologischen Raum „Lifting“, um dem gleichnamigen Konzept in der Kategorientheorie zu ähneln. Dabei handelt es sich um eine Transformation, die unter Einhaltung bestimmter Regeln hochdimensionale Zellen an den Eingabegraphen anhängt. Beispielsweise kann ein Diagramm zu einem Zellkomplex hochgestuft werden, indem an jede Klippe oder jeden Zyklus des Diagramms eine höherdimensionale Zelle angehängt wird. Dadurch wird der Graph durch einen anderen Raum ersetzt, der mehr Struktur aufweist und dem GNN eine bessere Rechenstruktur als der ursprüngliche Graph verleihen kann. Im Folgenden diskutieren wir die spezifischen Vorteile dieses Ansatzes.
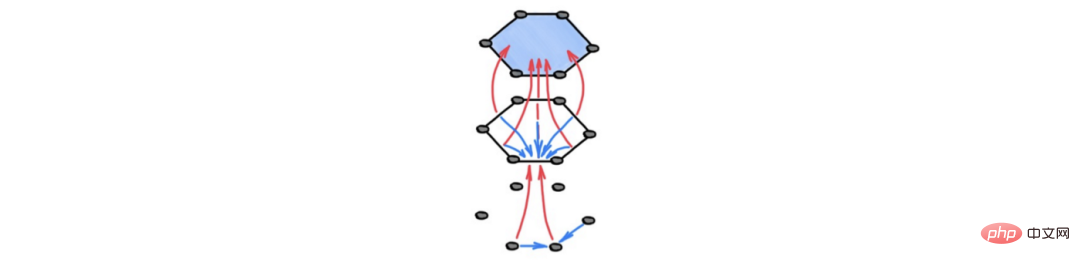
Bildunterschrift: Durch Kleben der Grenzen einer zweidimensionalen geschlossenen Scheibe an die induzierten Schleifen im Diagramm können hochdimensionale Zellkomplexe aus dem Diagramm konstruiert werden.
Merkmale und Strukturen höherer Ordnung
GNN verwendet normalerweise eine knotenzentrierte Sichtweise, und die an den Kanten vorhandenen Daten werden nur als Hilfsinformationen betrachtet, um die Kommunikation zwischen Scheitelpunkten zu verbessern. Bei der topologischen Informationsübertragung sind alle Einheiten erstklassige Bürger. Unabhängig von ihrer Größe wird ihnen eine spezifische Darstellung zugewiesen, die durch den Austausch von Informationen mit benachbarten Einheiten entwickelt wird. Dies bietet ein Rezept für die explizite Modellierung bestimmter Strukturen höherer Ordnung und der Wechselwirkungen zwischen ihnen. Insbesondere bietet es einen prinzipiellen Ansatz zur Entwicklung der Kantenmerkmale (d. h. 1 Einheit) des Eingabegraphen, was ein Problem darstellt, das von einer großen Klasse von GNN-Modellen nicht berücksichtigt wird.
Interaktionen höherer Ordnung
Diagramme sind per Definition binär („paarweise“) und können keine Beziehungen und Interaktionen darstellen, an denen mehr als zwei Objekte beteiligt sind. Dies kann ein Problem sein, wenn komplexe Systeme modelliert werden, die durch Wechselwirkungen höherer Ordnung gekennzeichnet sind: Beispielsweise könnten drei Reaktanten in einer chemischen Reaktion gleichzeitig interagieren. In einem Zellkomplex kann diese Situation durch die Verbindung von Reaktanten zwischen zwei Zellen (d. h. ein „gefülltes“ Dreieck) kodiert werden. Daher wird der Rechenfluss des Modells an das Vorhandensein von Wechselwirkungen höherer Ordnung angepasst.
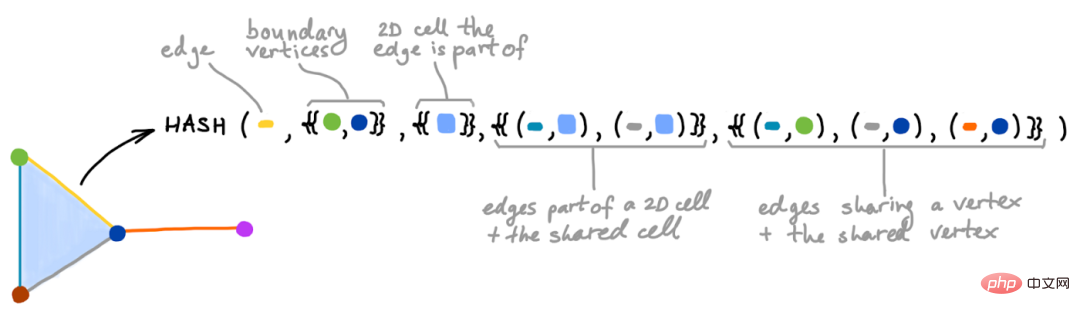
Bildunterschrift: Zell-Weisfeiler-Lehman-Test (CWL), der den klassischen WL-Test auf Zellpopulationen erweitert. Jeder Schritt des Algorithmus hasht die Farben benachbarter Zellen perfekt (es können unterschiedliche Dimensionen vorhanden sein).
Ausdruckskraft
Die Ausdruckskraft von Informationen, die GNNs passieren, wird durch den Weisfeiler-Leman (WL)-Graphisomorphismustest begrenzt. Es ist bekannt, dass WL bestimmte Graphunterstrukturen wie Dreiecke oder Kreise nicht erkennen kann, selbst sehr einfache Nichtstrukturen - Auch isomorphe Bilder sind nicht zu unterscheiden.
Laut früheren Arbeiten (Papieradresse: https://arxiv.org/abs/2103.03212; https://arxiv.org/abs/2106.12575), WL-Test (CWL) Der Mobilfunk Version kann verwendet werden, um den Isomorphismus zellulärer Komplexe zu testen. Wenn dieser neue Test mit dem oben beschriebenen Graph-Lifting-Verfahren abgeglichen wird, stellt man fest, dass er größere Graphklassen unterscheiden kann als der WL-Test. Daher erbt der topologische Informationsübertragungsprozess unter bestimmten Bedingungen die Vorteile dieses Tests und verbessert die Ausdrucksfähigkeit im Vergleich zum Standard-GNN. Unzureichende, übermäßige Glättung und Engpässe
GNN für die Informationsübertragung erfordert n Schichten, um die Kommunikation von Knoten zu ermöglichen, die n Hops voneinander entfernt sind. Wenn nur wenige Schichten verwendet werden, sodass weit voneinander entfernte Knoten keineInformationen austauschen können, wird dieses Phänomen als Unterreichweite bezeichnet.
Im Gegensatz dazu kann die Verwendung zu vieler Ebenen zu einer übermäßigen Glättung führen und Informationen können in strukturellen Engpässen des Diagramms verloren gehen.Einheitskomplexe können diese Probleme lindern, da die durch hochdimensionale Einheiten induzierte reichhaltigere Nachbarschaftsstruktur Verknüpfungen zwischen Knoten schafft, die möglicherweise weit voneinander entfernt sind. Daher müssen Informationen nur einige Rechenschritte enthalten, um verbreitet zu werden, um gültig zu sein.
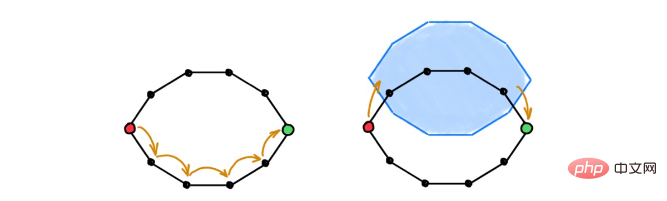
Bildunterschrift: GNN benötigt viele Schichten, um die Kommunikation weit voneinander entfernter Knoten zu ermöglichen (links). Hochdimensionale Zellen verändern die zugrunde liegende Topologie des Raums, indem sie Verknüpfungen erstellen (rechts). Dadurch können entfernte Knoten Informationen in mehreren Nachrichtenschritten austauschen. Hierarchische Modellierung
TopologieInformationDie durch Informationsweitergabe durchgeführten Berechnungen sind hierarchisch und Informationsflüsse von niedrigdimensionalen Einheiten zu hochdimensionalen Einheiten und zurück, was als „vertikal“ (und differenzierbar) betrachtet werden kann ) Pool Eine Form des Poolings anstelle des „horizontalen“ Poolings in standardmäßigen graphischen neuronalen Netzen. Dadurch bleibt die induktive Tendenz „komprimierter“ Diagrammbereiche erhalten, ohne dass feinkörnige Informationen des Eingabediagramms ignoriert werden, die die GNN-Pooling-basierte Leistung beeinträchtigen würden.
Bildunterschrift: Topologische Informationsübertragung ermöglicht die geschichtete Existenz von Informationen zwischen Einheiten unterschiedlicher Dimensionen
Domänenausrichtung
Bestimmte Anwendungen stehen auf natürliche Weise im Einklang mit der Struktur zellulärer Komplexe, z. B. Atome, Bindungen und chemische Ringe dargestellt als 0-Zelle, 1-Zelle und 2-Zelle. Die direkte Entsprechung zwischen der physikalischen Struktur des Moleküls und der komplexen Darstellung der Zelle ermöglicht die Übertragung topologischer Informationen, um die oben genannten Eigenschaften zu nutzen Der Informationstransfer erzielt modernste Ergebnisse bei der Vorhersage molekularer Eigenschaften.
Andere Anwendungen, die eine gute Ausrichtung aufweisen, können diskrete Mannigfaltigkeiten (Gitter) in Computergrafikanwendungen, soziale Netzwerke (Cliquen sind besonders wichtig) oder räumliche Diagramme wie Google Maps (Blöcke zwischen Straßen können auf natürliche Weise dargestellt werden) umfassen eine „kubische“ Zelle).
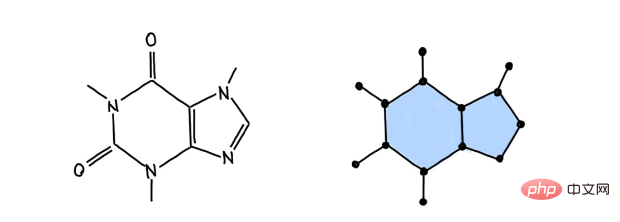
Bildunterschrift: Der Kaffeefaktor wird als zweidimensionaler Zellkomplex modelliert
2 Die Kombination von Topologie und Differentialgeometrie
Lochalgebra und Richtungsäquivalenz
In der algebraischen Topologie ist es üblich, gerichtete simpliziale Komplexe zu verwenden, bei denen es für jeden Simplex eine beliebige „Ausrichtung“ gibt, wir wählen beispielsweise einen Quellknoten und einen Zielknoten und Wählen Sie für jedes Dreieck eine Reihenfolge zum Durchlaufen seiner Knoten. Sobald die Richtungen ausgewählt sind, können interessante algebraische Operatoren auf komplexe Formen angewendet werden, beispielsweise die Berechnung der Grenzen bestimmter Simplexe mithilfe von „Grenzoperatoren“. Diese algebraischen Operationen können auch verwendet werden, um „Löcher“ in simplizialen Komplexen zu finden – Regionen, die keine Grenzen haben, aber nicht auf den Grenzen von etwas anderem liegen. Hinter den Kulissen stützt sich die persistente Homologie auf diese Berechnungen, um topologische Merkmale zu erkennen.
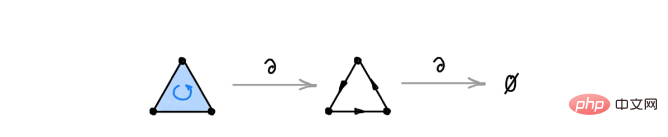
Bildunterschrift: Der auf einen 2-Simplex angewendete Randoperator erzeugt ein Dreieck. Wendet man den Operator erneut auf das Dreieck an, ist das Ergebnis Null, da das Dreieck ein Kreis ist und keine Grenzen hat.
Topologische Informationsübertragung kann als (nichtlineare) Verallgemeinerung algebraischer Operatoren (z. B. Randoperatoren) angesehen werden. Daher ist es notwendig, dass sich die topologische Informationsübertragung ähnlich verhält: Wir möchten, dass die Ausgabe jeder Schicht „gleichmäßig“ auf Änderungen in der Ausrichtung des Eingabekomplexes reagiert. Mit anderen Worten: Wir möchten, dass unsere Ebenen richtungsäquivalent sind. In unserer Arbeit untersuchen wir, wie die topologischeInformationsübertragung diese Eigenschaft erfüllt, indem wir geeignete Nichtlinearitäten und Informationsübertragungsfunktionen auswählen, und dies wird auch in einer reinen Faltungsumgebung untersucht. Unterscheiden Sie topologische RäumeEine der frühesten bekannten topologischen Invarianten, die Euler-Signatur, wurde ursprünglich bei der Klassifizierung platonischer Körper verwendet, die wir als alternierende Summe der Anzahl von Zellen in jeder Dimension definieren können. Wenn zwei Zellkomplexe homöomorph sind, sind diese Summen überraschenderweise konsistent, selbst wenn es sich um unterschiedliche Diskretisierungen desselben Raums handelt.
Interessanterweise erleichtert die Ausleseoperation des topologischen Informationsübertragungsmodells die Berechnung der Invarianz der Topologie, da auf jede Dimensionseinheit eine inklusive Invariantenreduktion angewendet wird.Daher kann dieser Modelltyp bestimmte nicht isomorphe Räume strukturell unterscheiden (dh unterschiedliche Euler-Eigenschaften aufweisen). Aus rechnerischer Sicht kann dies als eine Verallgemeinerung des WL-Tests angesehen werden, bei dem es uns nicht nur darum geht, festzustellen, ob zwei Zellkomplexe identisch sind, sondern auch, ob sie zueinander isomorph sind.
Die diskrete Hodge-Theorie bietet eine eher geometrische Erklärung für die topologischen Eigenschaften zellulärer Komplexe. Wenn das Vorzeichen der einer k-Zelle zugeordneten Merkmale von der Ausrichtung der k-Zelle abhängt, können diese Merkmale mathematisch als diskrete Versionen von differentiellen k-Formen in der Differentialgeometrie betrachtet werden (d. h. k-dimensionale Volumenelemente, die sein können). integriert). Ein Operator namens Hoch-Laplace-Operator verallgemeinert den grafischen Laplace-Operator und arbeitet mit diesen Differentialformen. Es kann bewiesen werden, dass die auf diesem Laplace-Operator basierende Diffusions-PDE im Grenzwert dem Signal konvergiert, das sich auf das Loch des Verbundwerkstoffs bezieht.
Bildunterschrift: Die partielle Diffusionsdifferentialgleichung basierend auf dem Hoch-Laplace-Operator konvergiert zum Grenzwert der Projektion der anfänglichen Differentialform auf den Laplace-Operatorkern. Dieses Bild zeigt, wie der Null-Eigenvektor des Hoch-Laplace-Operators um Löcher im Komplex hohe Werte annimmt. Das erste einfache neuronale Netzwerkmodell basierte tatsächlich auf dem Faltungsmodell von Hoch Laplace, das wiederum von der topologischen Signalverarbeitung inspiriert war. Erst kürzlich wurde eine auf diesem Operator basierende Version des Faltungsmodells verwendet, um NP-schwere Probleme in der rechnerischen algebraischen Topologie zu lösen. 3 abschließende Gedanken In neueren Arbeiten wird argumentiert, dass topologische Informationsübertragungsmethoden unter anderem nichts anderes als GNNs sind, die die Informationsübertragung auf modifizierten Graphen durchführen, die die Struktur zellulärer Komplexe kodieren. Dies gilt für Faltungsmodelle, bei denen die Berechnung der Informationsübertragung Zellpaare umfasst. Information in ihrer allgemeinsten Form einer hochdimensionalen Zelle, die Information-Informationen zu modulieren, die zwischen niederdimensionalen Zellen an ihrer Grenze übertragen werden. Im Allgemeinen können Informationen durch reguläre In beiden Fällen wird die Berechnung durch die Topologie des zugrunde liegenden Raums gesteuert, an den die Daten angehängt sind. Wir glauben, dass die Vorteile der Übernahme dieser topologischen Perspektive auf die Informationsübertragung über rein rechnerische Überlegungen hinausgehen. Neben wertvollen mathematischen Verbindungen öffnet es den Forschungsdiskurs für andere mathematische und rechnerische Disziplinen und erleichtert so eine positive gegenseitige Befruchtung zwischen unseren oft zu eintönigen Gemeinschaften. Was ist der nächste Schritt für die Weitergabe topologischer Informationen?
Zweitens werden weitere mathematische Objekte und Werkzeuge aus dem Bereich der algebraischen Topologie (einschließlich Strukturen wie Wabenscheiben, die selbst den mathematisch versiertesten ML-Forschern fremd klingen mögen) von der Graphen- und geometrischen Deep-Learning-Community übernommen . 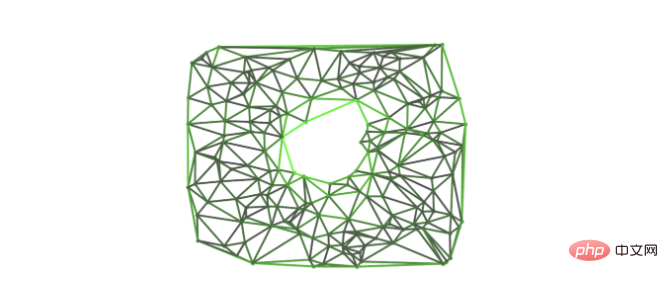
Allerdings ermöglicht die
Informationsfunktion Erstens können viele der im Laufe der Jahre in GNNs entwickelten Architekturen (z. B. Aufmerksamkeitsmechanismen) in diese neuen topologischen Räume übernommen und gleichzeitig genutzt werden spezifische Eigenschaften.
Das obige ist der detaillierte Inhalt vonMichael Bronstein greift auf die algebraische Topologie zurück und schlägt eine neue Computerstruktur für graphische neuronale Netze vor!. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Technologietrends, die Sie im Jahr 2023 im Auge behalten sollten
- Wie künstliche Intelligenz Rechenzentrumsteams neue Alltagsaufgaben beschert
- Können künstliche Intelligenz oder Automatisierung das Problem der geringen Energieeffizienz in Gebäuden lösen?
- OpenAI-Mitbegründer im Interview mit Huang Renxun: Die Argumentationsfähigkeiten von GPT-4 haben noch nicht die Erwartungen erfüllt
- Dank der OpenAI-Technologie übertrifft Bing von Microsoft Google im Suchverkehr

