Heim >Technologie-Peripheriegeräte >KI >Neueste PNAS-Forschung: 81 % Problemlösungsrate, neuronales Netzwerk Codex öffnet die Tür zur Welt der fortgeschrittenen Mathematik
Neueste PNAS-Forschung: 81 % Problemlösungsrate, neuronales Netzwerk Codex öffnet die Tür zur Welt der fortgeschrittenen Mathematik
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2023-04-09 15:51:061499Durchsuche
Kürzlich wurde in PNAS eine neue Studie veröffentlicht, die die Fähigkeiten neuronaler Netze noch einmal auffrischt. Dieses Mal wurde das neuronale Netzwerk verwendet, um fortgeschrittene Mathematikprobleme zu lösen, und es handelte sich um schwierige Mathematikprobleme im MIT-Mathematikkurs!
In dieser neuen Studie hat das Forschungsteam bewiesen, dass das Codex-Modell von OpenAI eine Programmsynthese zur Lösung großer mathematischer Probleme durchführen und 81 % der Mathematikkursprobleme im Datensatz durch Lernen kleiner Stichproben und Codex automatisch lösen kann Die Leistung bei diesen Aufgaben erreicht menschliches Niveau.
... zum Thema. Das Forschungsteam wies darauf hin, dass der Grund, warum Codex solche Fähigkeiten erreichen kann, gerade darin liegt, dass das Team eine große Innovation vorgenommen hat. Diese erfolglosen Studien verwendeten in der Vergangenheit nur textbasiertes Vortraining, das diesmal erschienene neuronale Codex-Netzwerk jedoch nicht Nur das Vortraining basiert auf Text und der Code wird ebenfalls verfeinert. 
Der untersuchte Problemdatensatz wurde aus sechs Mathematikkursen am MIT und einem Mathematikkurs an der Columbia University ausgewählt. 25 Probleme wurden zufällig aus sieben Kursen ausgewählt: Einzelvariablenrechnung, Multivariablenrechnung, Differentialrechnungen, Einführung in die Wahrscheinlichkeit und Statistik, lineare Algebra und Mathematik für Informatik und COMS3251 Computational Linear Algebra von der Columbia University.
Gleichzeitig verwendete das Forschungsteam MATH, einen neuesten Benchmark für fortgeschrittene Mathematikprobleme, der zur Bewertung des mathematischen Denkens verwendet wird, um die Fähigkeit des OpenAI-Codex zu testen. MATH deckt sechs Hauptbereiche der Mathematik ab: Elementaralgebra, Algebra, Zählen und Wahrscheinlichkeit und Mittelstufe Es gibt jeweils 15 Aufgaben aus den Bereichen Algebra, Zahlentheorie und Vorkalkulation.
Bildunterschrift: In der Studie verwendeter Kursfragendatensatz und MATH-Benchmark
Die Studie zeigte, dass Codex 213 der 265 Fragen im Fragendatensatz und im MATH-Datensatz automatisch gelöst hat. 
1 Wo ist die Innovation
Nach der Veröffentlichung von Transformer haben Transformer-basierte Sprachmodelle große Erfolge bei verschiedenen NLP-Aufgaben (Natural Language Processing) erzielt, einschließlich Zero-Shot- und Fence-Shot-Sprachaufgaben. Da Transformer jedoch nur auf Text vortrainiert ist, sind diese Modelle grundsätzlich nicht in der Lage, mathematische Probleme zu lösen. GPT-3 ist ein typisches Beispiel.Später wurden die mathematischen Denkfähigkeiten von GPT-3 durch Fow-Shot-Lernen und CoT-Eingabeaufforderungen verbessert; auch ohne Code ist GPT-3 jedoch besser immer noch machtlos bei mathematischen Problemen auf College-Niveau und dem MATH-Benchmark.
Frühere Forschungen zur Lösung mathematischer Probleme haben möglicherweise bestimmte Ergebnisse auf einem relativ einfachen mathematischen Niveau erzielt. Beispielsweise können Techniken, die Ausdrucksbäume auf der Grundlage kollaborativer Trainingsergebnisse validieren oder vorhersagen, wie MAWPS und Math23k, mathematische Probleme auf Grundschulniveau mit einer Genauigkeit von über 81 % lösen, aber sie können Mathematikprobleme auf Oberstufen-, Olympiade- oder College-Niveau nicht lösen Mathe-Aufgaben. Co-Training in Kombination mit graphischen neuronalen Netzen (GNN) zur Vorhersage arithmetischer Ausdrucksbäume ermöglicht die Lösung universitärer Probleme im maschinellen Lernen mit einer Genauigkeit von bis zu 95 %. Aber auch diese Arbeit beschränkte sich auf numerische Antworten, führte zu einer Überanpassung und konnte nicht auf andere Kurse übertragen werden.
Eine der größten Neuerungen dieser Arbeit
besteht darin, dass nicht nur das Transformer-Modell wie Codex vorab auf Text trainiert, sondern auch auf den Code abgestimmt wurde, sodass es groß angelegte mathematische Lösungen generieren kann Problemprogramm.
Das Forschungsteam wählte nach dem Zufallsprinzip Frageproben aus dem Datensatz aus, für deren Tests keine Eingabebilder oder Beweise erforderlich waren. Unter ihnen löste ein nur auf Text vorab trainiertes Sprachmodell (GPT-3 text-davinci-002) automatisch nur 18 % der Kursprobleme und 25,5 % der MATH-Benchmark-Probleme. Im Gegensatz dazu kann ein Programm, das mithilfe von Zero-Shot-Learning und einem neuronalen Netzwerk, das auf Text vortrainiert und auf Code abgestimmt wurde (OpenAI Codex code-davinci-002), synthetisiert wurde, 71 % der Kursprobleme und 72,2 % der Probleme automatisch lösen MATH-Benchmark-Fragen. Mit dem gleichen neuronalen Netzwerk Codex und dem Lernen mit wenigen Schüssen können 81 % der Probleme im Kurs und 81,1 % der Probleme im MATH-Benchmark-Test automatisch gelöst werden. Allerdings wurden 19 % der Kursfragen und 18,9 % der MATH-Benchmark-Fragen, die die übrigen Modelle nicht automatisch lösen konnten, letztendlich durch manuelle Eingabeaufforderungen gelöst. Die Hinzufügung der Lernmethode für kleine Stichproben ist die zweite große Innovation dieser Forschung. Wie aus der obigen Abbildung ersichtlich ist, wird, wenn Zero-Shot-Lernen die Frage nicht beantworten kann, ein (Frage-, Code-)Paar (Paar) verwendet, um Small-Shot-Lernen durchzuführen: 1) Unter Verwendung der Textähnlichkeit von OpenAI- babbage-001 Einbettungs-Engine bettet alle Fragen ein; 2) Berechnen Sie die ähnlichsten gelösten Fragen aus ihren Kursen mithilfe der eingebetteten Kosinusähnlichkeit; 3) Kombinieren Sie die ähnlichsten Fragen mit ihren entsprechenden Codes Beispiel für ein kleines Beispielproblem. Bildhinweis: Vergleich der automatischen Problemlösungsraten in 4 Methoden Shot-Learning. Vergleich der automatischen Problemlösungsraten zwischen 4 Methoden. Aus der Abbildung ist ersichtlich, dass der durch den orangefarbenen Balken dargestellte kleine Beispiel-Lerncodex eine hervorragende Leistung bei der automatischen Problemlösungsrate aufweist und in praktisch jedem mathematischen Bereich stärker ist als die der anderen drei Methoden. besteht darin, eine Pipeline zur Lösung mathematischer Probleme bereitzustellen und zu erklären, warum die Lösung so ist. Die folgende Abbildung zeigt den Ausführungsfluss der Pipeline in den 5 Mathematikkursen des MIT. Am Beispiel des Einzelvariablenkalkülproblems 18.01 wird Codex bei einem gegebenen Problem und dem automatisch generierten Präfix „SymPy verwenden“ aufgefordert und gibt ein Programm aus. Beim Ausführen des Programms wird eine Gleichung mit der richtigen Antwort erstellt. Das Programm fordert dann automatisch erneut zur Eingabe des Codex auf, was zu einer generierten Codeerklärung führt. 2 Nach dem Lösen von Problemen Um das Niveau der generierten Fragen zu bewerten, führte das Team eine Umfrage unter MIT-Studenten durch, die an diesen Kursen oder Kursen auf demselben Niveau teilgenommen hatten, hauptsächlich um die Qualität und den Schwierigkeitsgrad maschinell generierter und manuell geschriebener Fragen zu vergleichen Fragen. 1) Glauben Sie, dass diese Frage von Menschen geschrieben oder maschinell erstellt wurde? 2) Halten Sie diese Frage für einen bestimmten Kurs für angemessen oder unangemessen? 3) Wie würden Sie den Schwierigkeitsgrad dieser Frage auf einer Skala von 1 (am einfachsten) und 5 (am schwierigsten) einstufen? In den zurückgesendeten Fragebögen sind die Ergebnisse der Schülerbefragung wie folgt zusammengefasst: Die maschinell generierten Fragen haben es den Schülern erschwert, sie zu unterscheiden, was darauf hindeutet, dass Codex bei der Generierung neuer Inhalte das menschliche Leistungsniveau erreicht hat. Das Modell hat jedoch auch Probleme, die nicht gelöst werden können, z. B. wenn die Frage in einem Bild oder einer anderen nicht-textuellen Form erscheint, kann sie nicht mit a beantwortet werden Die Lösung muss bewiesen werden. Dieses Modell kann auch keine Programmprobleme oder rechentechnisch schwierigen Probleme wie die Faktorisierung sehr großer Primzahlen lösen. Diese letzte Art von Fragen sollte jedoch in keinem Mathematikkurs auftauchen, da selbst echte Studierende sie nicht beantworten können. 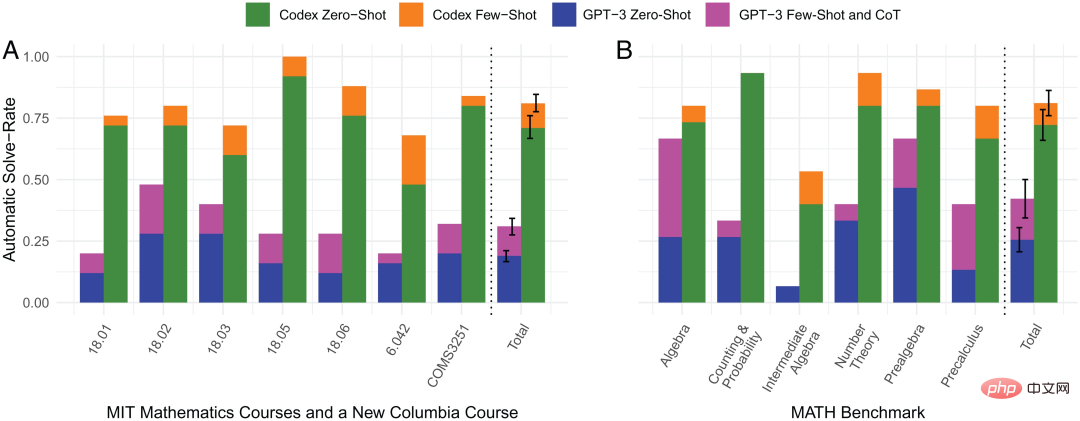 Die
Die 
In jedem der 6 Kurse des MIT werden 5 handgeschriebene Fragen und 5 modellgenerierte Fragen gemischt und zufällig präsentiert. Für jede der 60 Fragen wurden die teilnehmenden Schüler gebeten, drei Umfragefragen zu beantworten:
Das obige ist der detaillierte Inhalt vonNeueste PNAS-Forschung: 81 % Problemlösungsrate, neuronales Netzwerk Codex öffnet die Tür zur Welt der fortgeschrittenen Mathematik. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Technologietrends, die Sie im Jahr 2023 im Auge behalten sollten
- Wie künstliche Intelligenz Rechenzentrumsteams neue Alltagsaufgaben beschert
- Können künstliche Intelligenz oder Automatisierung das Problem der geringen Energieeffizienz in Gebäuden lösen?
- OpenAI-Mitbegründer im Interview mit Huang Renxun: Die Argumentationsfähigkeiten von GPT-4 haben noch nicht die Erwartungen erfüllt
- Dank der OpenAI-Technologie übertrifft Bing von Microsoft Google im Suchverkehr

