Heim >Technologie-Peripheriegeräte >KI >Was haben Tongji und Alibaba bei den CVPR 2022 Best Student Paper Awards untersucht? Dies ist eine Interpretation eines Werkes
Was haben Tongji und Alibaba bei den CVPR 2022 Best Student Paper Awards untersucht? Dies ist eine Interpretation eines Werkes
- PHPznach vorne
- 2023-04-09 13:41:091596Durchsuche
In diesem Artikel wird unsere Arbeit „EPro-PnP: Generalized End-to-End Probabilistic Perspective-n-Points for Monocular Object Pose Estimation“ erläutert, die mit dem CVPR 2022 Best Student Paper Award ausgezeichnet wurde. Das in dieser Arbeit untersuchte Problem besteht darin, die Pose eines Objekts im 3D-Raum anhand eines einzelnen Bildes abzuschätzen. Unter den vorhandenen Methoden extrahieren Posenschätzungsmethoden, die auf der geometrischen PnP-Optimierung basieren, häufig 2D-3D-Korrelationspunkte über tiefe Netzwerke. Da die optimale Lösung der Pose jedoch während der Rückausbreitung nicht differenzierbar ist, ist es schwierig, Posenfehler als Verlustleistung zu verwenden Stabiles End-to-End-Training des Netzwerks, wenn die 2D-3D-Korrelationspunkte auf der Überwachung anderer Agentenverluste beruhen, was kein optimales Trainingsziel für die Posenschätzung ist.
Um dieses Problem zu lösen, haben wir basierend auf der Theorie das EPro-PnP-Modul vorgeschlagen, das die Wahrscheinlichkeitsdichteverteilung der Pose anstelle einer einzelnen optimalen Lösung der Pose ausgibt und dadurch die undifferenzierbare optimale Pose durch differenzierbare ersetzt Wahrscheinlichkeitsdichte, stabiles End-to-End-Training wird erreicht. EPro-PnP ist äußerst vielseitig und eignet sich für verschiedene spezifische Aufgaben und Daten. Es kann zur Verbesserung bestehender PnP-basierter Posenschätzungsmethoden verwendet werden oder seine Flexibilität auch zum Trainieren neuer Netzwerke nutzen. Im allgemeineren Sinne bringt EPro-PnP im Wesentlichen die gemeinsame Klassifizierung Softmax in den kontinuierlichen Bereich und kann theoretisch erweitert werden, um allgemeine Modelle mit verschachtelten Optimierungsschichten zu trainieren.

Paper Link: https://arxiv.org/abs/2203.13254
code Link: https://github.com/tjiiv-cprg/epro-pnp
1. Einführung
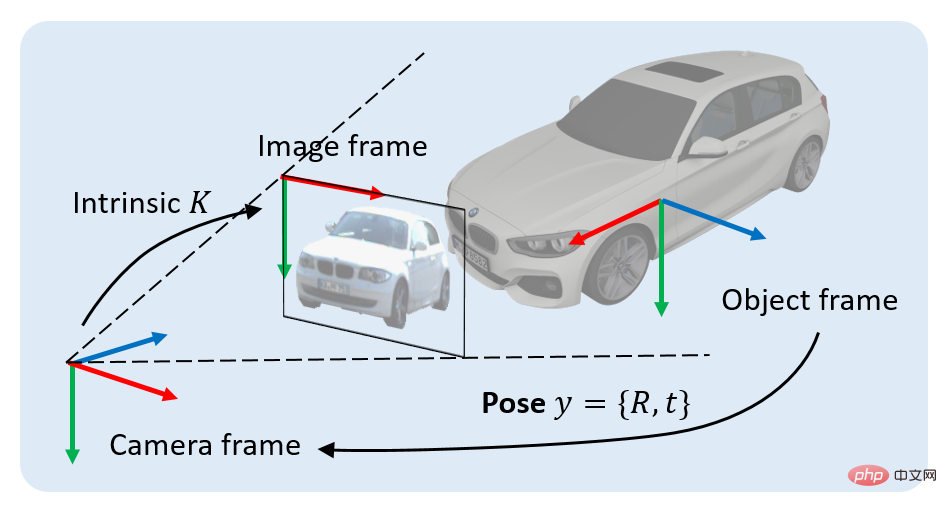
Wir untersuchen ein klassisches Problem der 3D-Vision: das Auffinden von 3D-Objekten basierend auf einem einzelnen RGB-Bild. Konkret besteht unser Ziel bei einem Bild, das eine Projektion eines 3D-Objekts enthält, darin, die Starrkörpertransformation vom Objektkoordinatensystem zum Kamerakoordinatensystem zu bestimmen. Diese Starrkörpertransformation wird als Pose des Objekts bezeichnet, die als y bezeichnet wird und zwei Teile enthält: 1) Positionskomponente, die durch einen 3x1-Verschiebungsvektor t dargestellt werden kann, 2) Orientierungskomponente, die durch eine 3x3-Rotation dargestellt werden kann Matrix R bedeutet.
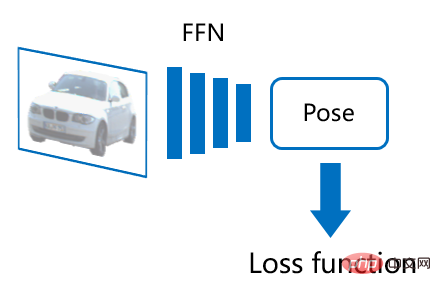
Um dieses Problem anzugehen, können bestehende Methoden in zwei Kategorien unterteilt werden: explizit und implizit. Die explizite Methode kann auch als direkte Posenvorhersage bezeichnet werden, das heißt, sie verwendet ein Feedforward-Neuronales Netzwerk (FFN), um jede Komponente der Pose des Objekts direkt auszugeben, normalerweise: 1) die Tiefe des Objekts vorhersagen, 2) finden die Mitte des Objekts Die 2D-Projektionsposition des Punkts auf dem Bild, 3) Vorhersage der Ausrichtung des Objekts (die spezifische Verarbeitungsmethode der Ausrichtung kann komplizierter sein). Unter Verwendung von Bilddaten, die mit der wahren Pose des Objekts markiert sind, kann eine Verlustfunktion entworfen werden, um die Ergebnisse der Posenvorhersage direkt zu überwachen und so auf einfache Weise ein durchgängiges Training des Netzwerks zu erreichen. Allerdings mangelt es solchen Netzwerken an Interpretierbarkeit und sie neigen dazu, bei kleineren Datensätzen eine Überanpassung vorzunehmen. Bei 3D-Objekterkennungsaufgaben dominieren explizite Methoden, insbesondere bei größeren Datensätzen (z. B. nuScenes).
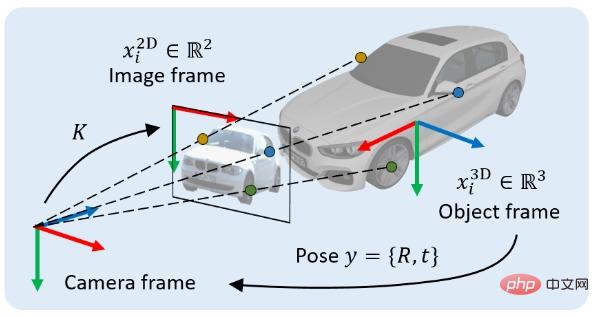

Die implizite Methode ist eine Posenschätzungsmethode basierend auf geometrischer Optimierung. Der typischste Vertreter ist die Pose-Schätzmethode basierend auf PnP. Bei dieser Art von Methode müssen Sie zunächst N 2D-Punkte im Bildkoordinatensystem finden (die 2D-Koordinaten des i-ten Punkts werden als  bezeichnet) und gleichzeitig die N damit verbundenen 3D-Punkte finden im Objektkoordinatensystem (dem i-ten Punkt) sind die 3D-Koordinaten des Punktes i als
bezeichnet) und gleichzeitig die N damit verbundenen 3D-Punkte finden im Objektkoordinatensystem (dem i-ten Punkt) sind die 3D-Koordinaten des Punktes i als  gekennzeichnet, und manchmal ist es notwendig, das Assoziationsgewicht jedes Punktpaares (das Assoziationsgewicht des i-ten) zu ermitteln. Das Punktepaar ist mit
gekennzeichnet, und manchmal ist es notwendig, das Assoziationsgewicht jedes Punktpaares (das Assoziationsgewicht des i-ten) zu ermitteln. Das Punktepaar ist mit  gekennzeichnet). Gemäß der perspektivischen Projektionsbeschränkung definieren diese N Paare von 2D-3D-gewichteten zugeordneten Punkten implizit die optimale Pose des Objekts. Konkret können wir die Objektpose
gekennzeichnet). Gemäß der perspektivischen Projektionsbeschränkung definieren diese N Paare von 2D-3D-gewichteten zugeordneten Punkten implizit die optimale Pose des Objekts. Konkret können wir die Objektpose  finden, die den Reprojektionsfehler minimiert:
finden, die den Reprojektionsfehler minimiert:
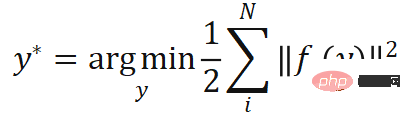
wobei 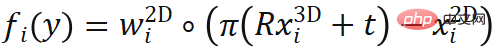 den gewichteten Reprojektionsfehler darstellt, der die
den gewichteten Reprojektionsfehler darstellt, der die  -Funktion der Pose ist.
-Funktion der Pose ist.  stellt die Kameraprojektionsfunktion dar, die interne Parameter enthält, und
stellt die Kameraprojektionsfunktion dar, die interne Parameter enthält, und 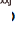 stellt das Elementprodukt dar. PnP-Methode wird häufig bei 6-DOF-Posenschätzungsaufgaben verwendet, bei denen die Objektgeometrie bekannt ist.
stellt das Elementprodukt dar. PnP-Methode wird häufig bei 6-DOF-Posenschätzungsaufgaben verwendet, bei denen die Objektgeometrie bekannt ist.
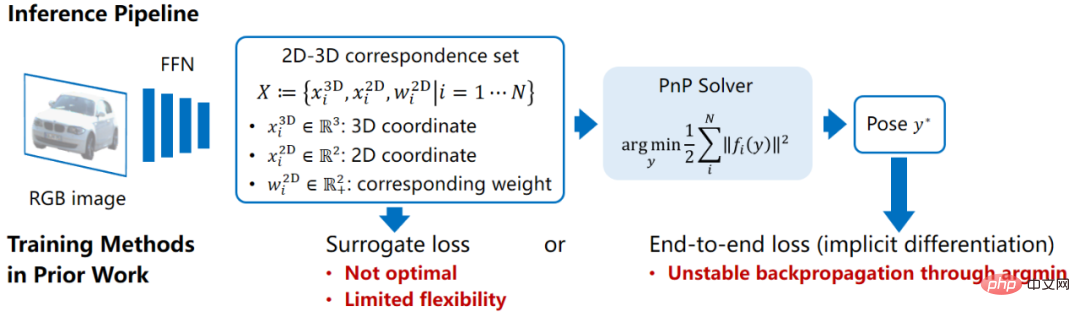
Die PnP-basierte Methode erfordert auch ein Feedforward-Netzwerk, um den 2D-3D-zugehörigen Punktsatz vorherzusagen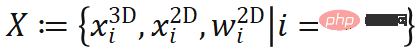 . Im Vergleich zur direkten Posenvorhersage ist dieses Deep-Learning-Modell in Kombination mit herkömmlichen geometrischen Sehalgorithmen sehr gut interpretierbar und seine Generalisierungsleistung ist relativ stabil. Allerdings weisen die Modelltrainingsmethoden in früheren Arbeiten Mängel auf. Viele Methoden konstruieren eine Proxy-Verlustfunktion, um das Zwischenergebnis X zu überwachen, was kein optimales Ziel für Pose darstellt. Wenn beispielsweise die Form des Objekts bekannt ist, können die 3D-Schlüsselpunkte des Objekts im Voraus ausgewählt werden, und dann wird das Netzwerk trainiert, um die entsprechende 2D-Projektionspunktposition zu finden. Dies bedeutet auch, dass der Ersatzverlust nur einige der Variablen in X lernen kann und daher nicht flexibel genug ist. Was ist, wenn wir die Formen der Objekte im Trainingssatz nicht kennen und alles in X von Grund auf lernen müssen?
. Im Vergleich zur direkten Posenvorhersage ist dieses Deep-Learning-Modell in Kombination mit herkömmlichen geometrischen Sehalgorithmen sehr gut interpretierbar und seine Generalisierungsleistung ist relativ stabil. Allerdings weisen die Modelltrainingsmethoden in früheren Arbeiten Mängel auf. Viele Methoden konstruieren eine Proxy-Verlustfunktion, um das Zwischenergebnis X zu überwachen, was kein optimales Ziel für Pose darstellt. Wenn beispielsweise die Form des Objekts bekannt ist, können die 3D-Schlüsselpunkte des Objekts im Voraus ausgewählt werden, und dann wird das Netzwerk trainiert, um die entsprechende 2D-Projektionspunktposition zu finden. Dies bedeutet auch, dass der Ersatzverlust nur einige der Variablen in X lernen kann und daher nicht flexibel genug ist. Was ist, wenn wir die Formen der Objekte im Trainingssatz nicht kennen und alles in X von Grund auf lernen müssen?
Die Vorteile expliziter und impliziter Methoden ergänzen sich. Wenn das Netzwerk durchgängig trainiert werden kann, um die zugehörige Punktmenge X zu lernen, indem die von PnP ausgegebenen Posenergebnisse überwacht werden, können die Vorteile beider kombiniert werden. Um dieses Ziel zu erreichen, haben einige neuere Studien die Rückausbreitung von PnP-Schichten mithilfe impliziter Funktionsableitung implementiert. Allerdings ist die Argmin-Funktion in PnP an bestimmten Punkten diskontinuierlich und nicht differenzierbar, was die Backpropagation instabil macht und es schwierig macht, direktes Training zu konvergieren.
2. Einführung in die EPro-PnP-Methode
1. EPro-PnP-Modul

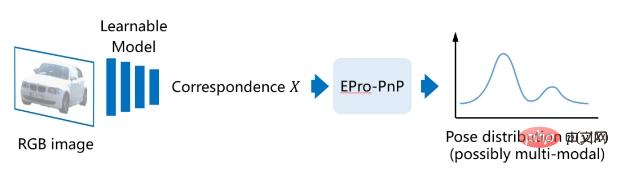
# 🎜🎜#Um ein stabiles End-to-End-Training zu erreichen, haben wir End-to-End-Probabilistisches PnP (End-to-End-Probabilistisches PnP) vorgeschlagen, also EPro-PnP# 🎜🎜# . Die Grundidee besteht darin, die implizite Pose als Wahrscheinlichkeitsverteilung zu betrachten, dann ist ihre Wahrscheinlichkeitsdichte für X differenzierbar. Definieren Sie zunächst die Wahrscheinlichkeitsfunktion der Pose basierend auf dem Reprojektionsfehler: 
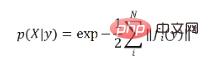

# 🎜🎜#. Tatsächlich besteht die Essenz von EPro-PnP darin, Softmax von einem diskreten Schwellenwert zu einem kontinuierlichen Schwellenwert und einer Summierung zu bewegen.# 🎜🎜#
wurde durch Punkte ersetzt. 🎜🎜#.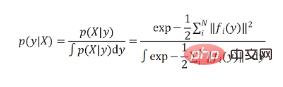
 2. KL-Divergenzverlust
2. KL-Divergenzverlust
Während des Trainings erkennt das Modell die wahre Pose des bekannten Objekts#🎜 🎜 # , Sie können die Zielposenverteilung
, Sie können die Zielposenverteilung  definieren. Zu diesem Zeitpunkt kann die KL-Divergenz
definieren. Zu diesem Zeitpunkt kann die KL-Divergenz  als Verlustfunktion berechnet werden, die zum Trainieren des Netzwerks verwendet wird (da
als Verlustfunktion berechnet werden, die zum Trainieren des Netzwerks verwendet wird (da
der Dirac-Funktion nähert, kann die auf der KL-Divergenz basierende Verlustfunktion auf die folgende Form vereinfacht werden: 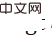 #🎜 🎜#
#🎜 🎜# Wenn man die Ableitung nimmt:
Wenn man die Ableitung nimmt: 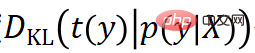
Es ist ersichtlich, dass die Verlustfunktion aus zwei Elementen besteht. Der erste Term (bezeichnet als  ) versucht, den Reprojektionsfehler des wahren Werts der Pose
) versucht, den Reprojektionsfehler des wahren Werts der Pose  zu reduzieren, und der zweite Term (bezeichnet als
zu reduzieren, und der zweite Term (bezeichnet als  ) versucht, die Vorhersage zu erhöhen. Reprojektionsfehler überall in der Pose
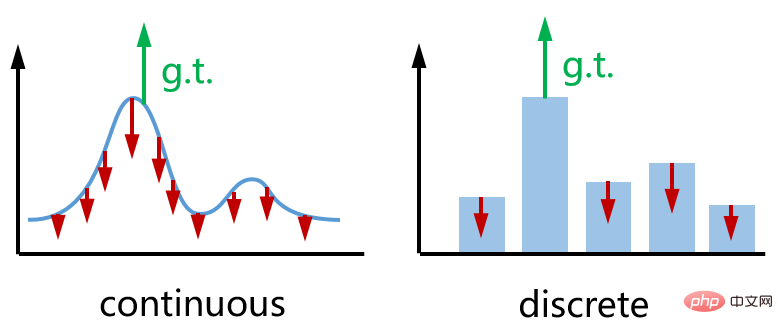
) versucht, die Vorhersage zu erhöhen. Reprojektionsfehler überall in der Pose  . Die beiden Richtungen sind entgegengesetzt und der Effekt ist in der Abbildung unten (links) dargestellt. Als Analogie sehen Sie rechts den kategorialen Kreuzentropieverlust, den wir üblicherweise beim Training von Klassifizierungsnetzwerken verwenden. 3. Monte-Carlo-Verlust Unter Berücksichtigung der Vielseitigkeit, Genauigkeit und Recheneffizienz verwenden wir die Monte-Carlo-Methode, um die Posenverteilung durch Stichproben zu simulieren.
. Die beiden Richtungen sind entgegengesetzt und der Effekt ist in der Abbildung unten (links) dargestellt. Als Analogie sehen Sie rechts den kategorialen Kreuzentropieverlust, den wir üblicherweise beim Training von Klassifizierungsnetzwerken verwenden. 3. Monte-Carlo-Verlust Unter Berücksichtigung der Vielseitigkeit, Genauigkeit und Recheneffizienz verwenden wir die Monte-Carlo-Methode, um die Posenverteilung durch Stichproben zu simulieren.
mit Gewichten 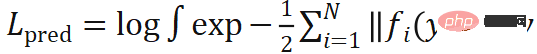 zu berechnen. Wir werden diesen Prozess als Monte-Carlo-PnP bezeichnen:
zu berechnen. Wir werden diesen Prozess als Monte-Carlo-PnP bezeichnen:

Dementsprechend kann der zweite Term 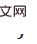 als Funktion des Gewichts
als Funktion des Gewichts 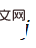 angenähert werden, und
angenähert werden, und
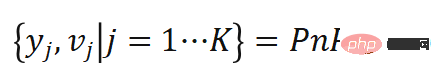 kann zurückpropagiert werden:
kann zurückpropagiert werden:
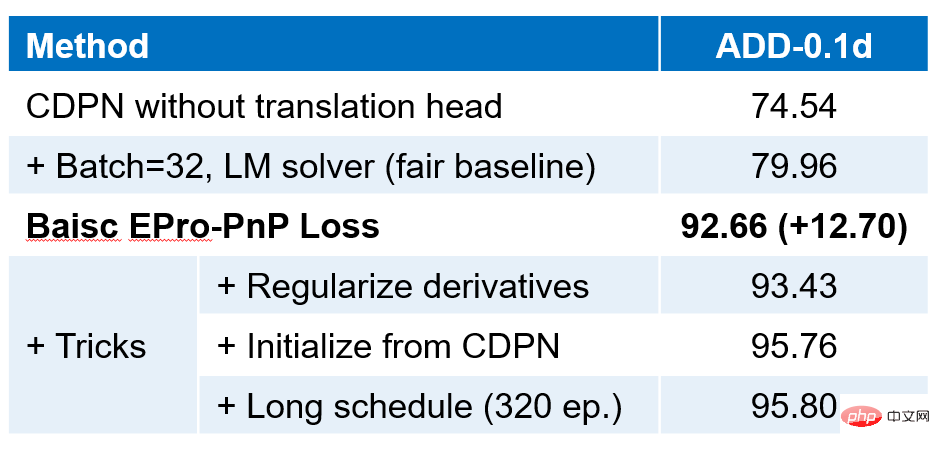
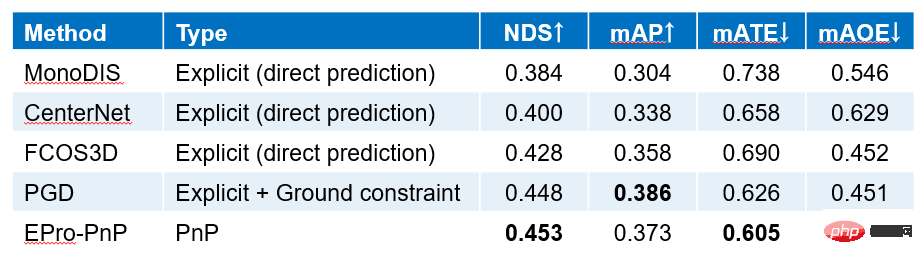
Obwohl der Monte-Carlo-PnP-Verlust zum Trainieren des Netzwerks verwendet werden kann, um eine qualitativ hochwertige Posenverteilung zu erhalten, ist es in der Inferenzphase immer noch notwendig, die optimale Position durch den PnP-Optimierungslöser zu erhalten Lösung wobei Wir verwenden unterschiedliche Netzwerke für die beiden Teilaufgaben der Posenschätzung mit 6 Freiheitsgraden und der 3D-Zielerkennung. Unter anderem wurde es für die Posenschätzung mit 6 Freiheitsgraden leicht modifiziert, basierend auf dem CDPN-Netzwerk von ICCV 2019, und wurde mit EPro-PnP trainiert, um Ablationsstudien für die 3D-Zielerkennung durchzuführen auf FCOS3D von ICCVW 2021 Deformierbarer Korrespondenzerkennungskopf, um zu beweisen, dass EPro-PnP das Netzwerk trainieren kann, alle 2D-3D-Punkte und Assoziationsgewichte ohne Kenntnis der Objektform direkt zu lernen, wodurch die Flexibilität von EPro-PnP in Anwendungen demonstriert wird. Die Netzwerkstruktur ist wie in der Abbildung oben dargestellt, mit der Ausnahme, dass die Ausgabeschicht basierend auf dem ursprünglichen CDPN geändert wird. Das ursprüngliche CDPN verwendet die 2D-Box des erkannten Objekts, um das regionale Bild auszuschneiden und es in den ResNet34-Backbone einzugeben. Das ursprüngliche CDPN entkoppelt Position und Orientierung in zwei Zweige. Der Positionszweig verwendet die explizite Methode der direkten Vorhersage, während der Orientierungszweig die implizite Methode der dichten Assoziation und PnP verwendet. Um EPro-PnP zu untersuchen, behält das modifizierte Netzwerk nur den dichten Korrelationszweig bei, dessen Ausgabe eine 3-Kanal-3D-Koordinatenkarte ist, und ein 2-Kanal-Korrelationsgewicht, wobei das Korrelationsgewicht einer räumlichen Softmax- und globalen Gewichtsskalierung unterzogen wurde. Der Zweck des Hinzufügens von räumlichem Softmax besteht darin, das Gewicht Die Netzwerkstruktur ist wie folgt oben Wie in der Abbildung gezeigt. Im Allgemeinen basiert es auf dem FCOS3D-Detektor und bezieht sich auf die von deformierbarem DETR entworfene Netzwerkstruktur. Auf der Basis von FCOS3D bleiben die Zentrier- und Klassifizierungsebenen erhalten und die ursprüngliche Posenvorhersageebene wird durch Objekteinbettungs- und Referenzpunktebenen zur Generierung von Objektabfragen ersetzt. In Bezug auf verformbares DETR erhalten wir die 2D-Abtastposition, indem wir den Versatz relativ zum Referenzpunkt vorhersagen (wir erhalten also Verwenden Sie das LineMOD-Datensatzexperiment und vergleichen Sie es genau mit der CDPN-Basislinie. Die Hauptergebnisse sind wie oben. Es ist ersichtlich, dass durch das Hinzufügen von EPro-PnP-Verlusten für das End-to-End-Training die Genauigkeit erheblich verbessert wird (+12,70). Erhöhen Sie den Verlust der abgeleiteten Regularisierung weiter, und die Genauigkeit wird weiter verbessert. Auf dieser Grundlage kann die Verwendung der Trainingsergebnisse des ursprünglichen CDPN zum Initialisieren und Erhöhen der Epochen (wobei die Gesamtzahl der Epochen mit dem vollständigen dreistufigen Training des ursprünglichen CDPN konsistent bleibt) die Genauigkeit weiter verbessern. Die Ausbildung CDPN geht aus der Zusatzausbildung CDPN-Maskenaufsicht hervor. Das Bild oben ist ein Vergleich von EPro-PnP mit verschiedenen führenden Methoden. EPro-PnP, das gegenüber dem Rückwärts-CDPN verbessert wurde, kommt der Genauigkeit von SOTA nahe und die Architektur von EPro-PnP ist einfach. Es basiert vollständig auf PnP für die Posenschätzung und erfordert keine zusätzliche explizite Tiefenschätzung oder Posenverfeinerung. Daher ergeben sich auch Effizienzvorteile. Unter Verwendung des nuScenes-Datensatzexperiments sind die Ergebnisse im Vergleich zu anderen Methoden in der obigen Abbildung dargestellt. EPro-PnP weist nicht nur eine deutliche Verbesserung gegenüber FCOS3D auf, sondern übertrifft auch PGD, eine weitere verbesserte Version von SOTA und FCOS3D zu dieser Zeit. Noch wichtiger ist, dass EPro-PnP derzeit das einzige ist, das geometrische Optimierungsmethoden verwendet, um die Pose im nuScenes-Datensatz zu schätzen. Aufgrund des großen Umfangs des nuScenes-Datensatzes weist das durchgängig trainierte direkte Posenschätzungsnetzwerk bereits eine gute Leistung auf, und unsere Ergebnisse zeigen, dass durch durchgängiges Training eines auf geometrischer Optimierung basierenden Modells eine bessere Leistung erzielt werden kann Große Datenmengen. Hervorragende Leistung. Die obige Abbildung zeigt die Vorhersageergebnisse des mit EPro-PnP trainierten dichten Assoziationsnetzwerks. Unter anderem hebt das Korrelationsgewicht map Die Ergebnisse der 3D-Zielerkennung sind in der Abbildung oben dargestellt. Die obere linke Ansicht zeigt die vom Verformungskorrelationsnetzwerk abgetasteten 2D-Punktpositionen. Rot zeigt Punkte mit einer höheren horizontalen X-Komponente und Grün zeigt Punkte mit einer höheren vertikalen Y-Komponente an. Die grünen Punkte befinden sich im Allgemeinen am oberen und unteren Ende des Objekts. Ihre Hauptfunktion besteht darin, die Entfernung des Objekts über die Höhe des Objekts zu berechnen. Diese Funktion ist nicht künstlich festgelegt und vollständig das Ergebnis eines freien Trainings. Das Bild rechts zeigt die Erkennungsergebnisse in einer Draufsicht, wobei das blaue Wolkenbild die Verteilungsdichte des Mittelpunkts des Objekts darstellt und die Unsicherheit der Positionierung des Objekts widerspiegelt. Im Allgemeinen ist die Positionierungsunsicherheit entfernter Objekte größer als die von nahegelegenen Objekten. EPro-PnP wandelt die ursprüngliche undifferenzierbare optimale Pose in eine differenzierbare Posenwahrscheinlichkeitsdichte um, sodass das Posenschätzungsnetzwerk basierend auf der geometrischen PnP-Optimierung einen stabilen und flexiblen End-to-End-Zug erreichen kann. EPro-PnP kann auf allgemeine Probleme bei der Posenschätzung von 3D-Objekten angewendet werden. Selbst wenn die 3D-Objektgeometrie unbekannt ist, können die 2D-3D-assoziierten Punkte des Objekts durch End-to-End-Training gelernt werden. Daher erweitert EPro-PnP die Möglichkeiten des Netzwerkdesigns, wie beispielsweise unseres vorgeschlagenen Deformationskorrelationsnetzwerks, das bisher nicht trainierbar war. Darüber hinaus kann EPro-PnP auch direkt zur Verbesserung bestehender PnP-basierter Posenschätzungsmethoden verwendet werden, wodurch das Potenzial bestehender Netzwerke durch End-to-End-Training freigesetzt und die Genauigkeit der Posenschätzung verbessert wird. Im allgemeineren Sinne bringt EPro-PnP im Wesentlichen die gemeinsame Klassifizierung Softmax in den kontinuierlichen Bereich. Es kann nicht nur für andere 3D-Vision-Probleme basierend auf geometrischer Optimierung verwendet werden, sondern kann auch theoretisch erweitert werden, um allgemeine verschachtelte Optimierungsschichten zu trainieren .  Der Visualisierungseffekt von Pose Sampling ist angezeigt in der Abbildung unten:
Der Visualisierungseffekt von Pose Sampling ist angezeigt in der Abbildung unten: 
4. Ableitungsregularisierung für den PnP-Löser
 . Der häufig verwendete Gauß-Newton-Algorithmus und seine Ableitungen lösen
. Der häufig verwendete Gauß-Newton-Algorithmus und seine Ableitungen lösen  durch iterative Optimierung, und sein iteratives Inkrement wird durch die erste und zweite Ableitung der Kostenfunktion
durch iterative Optimierung, und sein iteratives Inkrement wird durch die erste und zweite Ableitung der Kostenfunktion  bestimmt. Um die Lösung
bestimmt. Um die Lösung 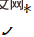 von PnP näher an den wahren Wert
von PnP näher an den wahren Wert  zu bringen, kann die Ableitung der Kostenfunktion reguliert werden. Die Regularisierungsverlustfunktion ist wie folgt aufgebaut:
zu bringen, kann die Ableitung der Kostenfunktion reguliert werden. Die Regularisierungsverlustfunktion ist wie folgt aufgebaut: 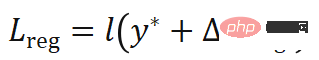
 das Gauss-Newton-Iterationsinkrement ist, das mit den Ableitungen erster und zweiter Ordnung der Kostenfunktion zusammenhängt und rückwärts propagiert werden kann ,
das Gauss-Newton-Iterationsinkrement ist, das mit den Ableitungen erster und zweiter Ordnung der Kostenfunktion zusammenhängt und rückwärts propagiert werden kann ,  stellt die Distanzmetriken dar, verwenden Sie Smooth L1 für die Position und Kosinusähnlichkeit für die Orientierung. Wenn
stellt die Distanzmetriken dar, verwenden Sie Smooth L1 für die Position und Kosinusähnlichkeit für die Orientierung. Wenn  inkonsistent ist, zwingt diese Verlustfunktion das Iterationsinkrement
inkonsistent ist, zwingt diese Verlustfunktion das Iterationsinkrement  dazu, auf den tatsächlichen wahren Wert zu zeigen.
dazu, auf den tatsächlichen wahren Wert zu zeigen. 3. Posenschätzungsnetzwerk basierend auf EPro-PnP
1. Dichtes Korrelationsnetzwerk für die 6-DOF-Posenschätzung
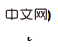 zu normalisieren, sodass es ähnliche Eigenschaften wie die Aufmerksamkeitskarte aufweist und sich auf relativ wichtige Bereiche konzentrieren kann. Schlüssel. Die globale Gewichtsskalierung spiegelt die Konzentration der Posenverteilung wider
zu normalisieren, sodass es ähnliche Eigenschaften wie die Aufmerksamkeitskarte aufweist und sich auf relativ wichtige Bereiche konzentrieren kann. Schlüssel. Die globale Gewichtsskalierung spiegelt die Konzentration der Posenverteilung wider  . Das Netzwerk kann nur mit dem Monte-Carlo-Posenverlust von EPro-PnP trainiert werden, zusätzlich zu einer abgeleiteten Regularisierung und einem zusätzlichen 3D-Koordinatenregressionsverlust, wenn die Objektform bekannt ist.
. Das Netzwerk kann nur mit dem Monte-Carlo-Posenverlust von EPro-PnP trainiert werden, zusätzlich zu einer abgeleiteten Regularisierung und einem zusätzlichen 3D-Koordinatenregressionsverlust, wenn die Objektform bekannt ist. 2. Verformungskorrelationsnetzwerk zur 3D-Zielerkennung
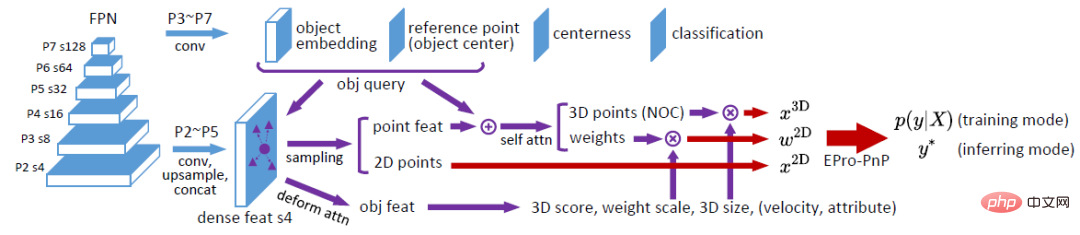
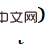 ). Die abgetasteten Merkmale werden durch Aufmerksamkeitsoperationen zu Objektmerkmalen aggregiert, die zur Vorhersage von Ergebnissen auf Objektebene (3D-Score, Gewichtsskala, 3D-Boxgröße usw.) verwendet werden. Darüber hinaus wird nach der Abtastung das Merkmal jedes Punkts durch Objekteinbettung hinzugefügt und durch Selbstaufmerksamkeit verarbeitet, um die 3D-Koordinaten auszugeben, die jedem Punkt entsprechen
). Die abgetasteten Merkmale werden durch Aufmerksamkeitsoperationen zu Objektmerkmalen aggregiert, die zur Vorhersage von Ergebnissen auf Objektebene (3D-Score, Gewichtsskala, 3D-Boxgröße usw.) verwendet werden. Darüber hinaus wird nach der Abtastung das Merkmal jedes Punkts durch Objekteinbettung hinzugefügt und durch Selbstaufmerksamkeit verarbeitet, um die 3D-Koordinaten auszugeben, die jedem Punkt entsprechen 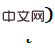 und das zugehörige Gewicht
und das zugehörige Gewicht 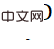 . Die vorhergesagten
. Die vorhergesagten  können alle durch den Monte-Carlo-Posenverlust von EPro-PnP trainiert werden, der ohne zusätzliche Regularisierung konvergieren und eine hohe Genauigkeit erreichen kann. Auf dieser Basis können abgeleitete Regularisierungsverluste und Hilfsverluste hinzugefügt werden, um die Genauigkeit weiter zu verbessern.
können alle durch den Monte-Carlo-Posenverlust von EPro-PnP trainiert werden, der ohne zusätzliche Regularisierung konvergieren und eine hohe Genauigkeit erreichen kann. Auf dieser Basis können abgeleitete Regularisierungsverluste und Hilfsverluste hinzugefügt werden, um die Genauigkeit weiter zu verbessern. 4. Experimentelle Ergebnisse
1, 6 Freiheitsgrade Posenschätzungsaufgabe

2. 3D-Zielerkennungsaufgabe
3. Visuelle Analyse
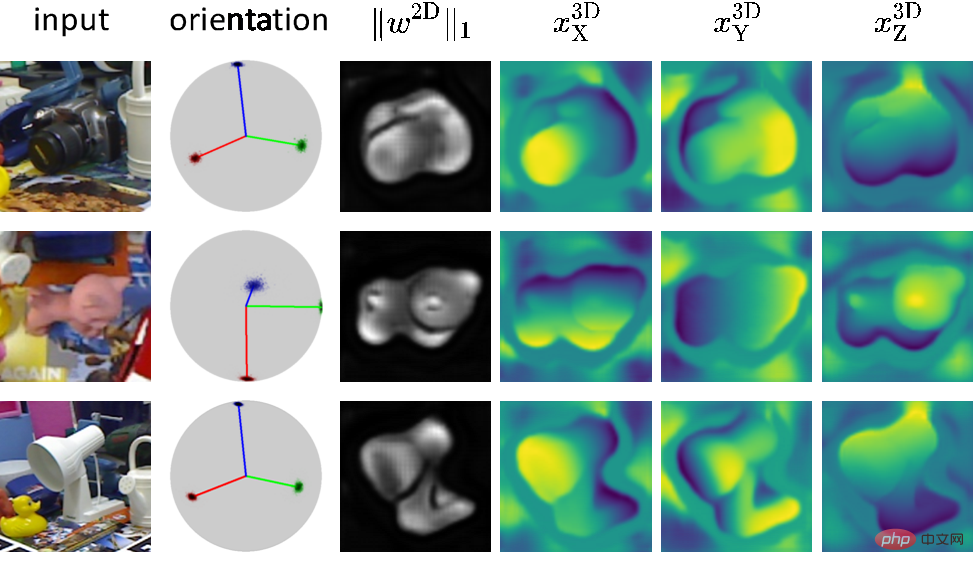
 wichtige Bereiche im Bild hervor, ähnlich dem Aufmerksamkeitsmechanismus. Aus der Verlustfunktionsanalyse ist ersichtlich, dass der hervorgehobene Bereich dem Bereich mit geringer Reprojektionsunsicherheit entspricht und empfindlicher auf Posenänderungen reagiert.
wichtige Bereiche im Bild hervor, ähnlich dem Aufmerksamkeitsmechanismus. Aus der Verlustfunktionsanalyse ist ersichtlich, dass der hervorgehobene Bereich dem Bereich mit geringer Reprojektionsunsicherheit entspricht und empfindlicher auf Posenänderungen reagiert. 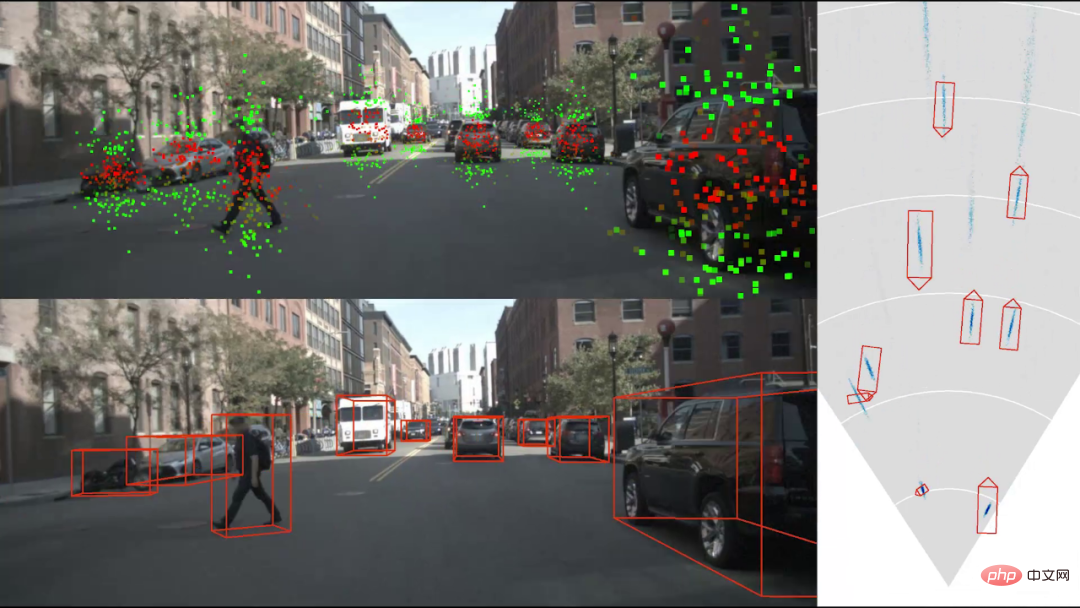

 Ein weiterer wichtiger Vorteil von EPro-PnP ist die Fähigkeit, Orientierungsmehrdeutigkeiten durch die Vorhersage komplexer multimodaler Verteilungen darzustellen. Wie in der Abbildung oben gezeigt, hat Barrier aufgrund der Rotationssymmetrie des Objekts selbst oft zwei Spitzen mit einem Unterschied von 180°; der Kegel selbst hat keine spezifische Ausrichtung, sodass die Vorhersageergebnisse nicht vollständig in alle Richtungen verteilt sind symmetrisch, aber aufgrund des Bildes ist es nicht klar, es ist schwer, Vorder- und Rückseite zu unterscheiden, und manchmal gibt es zwei Spitzen. Aufgrund dieser probabilistischen Eigenschaft erfordert EPro-PnP keine spezielle Verarbeitung der Verlustfunktion für symmetrische Objekte.
Ein weiterer wichtiger Vorteil von EPro-PnP ist die Fähigkeit, Orientierungsmehrdeutigkeiten durch die Vorhersage komplexer multimodaler Verteilungen darzustellen. Wie in der Abbildung oben gezeigt, hat Barrier aufgrund der Rotationssymmetrie des Objekts selbst oft zwei Spitzen mit einem Unterschied von 180°; der Kegel selbst hat keine spezifische Ausrichtung, sodass die Vorhersageergebnisse nicht vollständig in alle Richtungen verteilt sind symmetrisch, aber aufgrund des Bildes ist es nicht klar, es ist schwer, Vorder- und Rückseite zu unterscheiden, und manchmal gibt es zwei Spitzen. Aufgrund dieser probabilistischen Eigenschaft erfordert EPro-PnP keine spezielle Verarbeitung der Verlustfunktion für symmetrische Objekte. 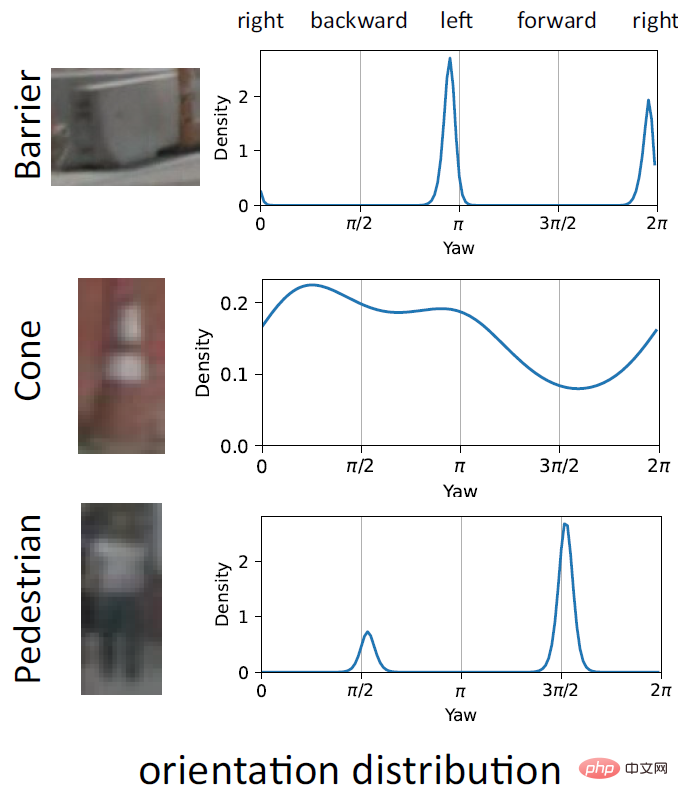 5. Zusammenfassung
5. Zusammenfassung
Das obige ist der detaillierte Inhalt vonWas haben Tongji und Alibaba bei den CVPR 2022 Best Student Paper Awards untersucht? Dies ist eine Interpretation eines Werkes. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Technologietrends, die Sie im Jahr 2023 im Auge behalten sollten
- Wie künstliche Intelligenz Rechenzentrumsteams neue Alltagsaufgaben beschert
- Können künstliche Intelligenz oder Automatisierung das Problem der geringen Energieeffizienz in Gebäuden lösen?
- OpenAI-Mitbegründer im Interview mit Huang Renxun: Die Argumentationsfähigkeiten von GPT-4 haben noch nicht die Erwartungen erfüllt
- Dank der OpenAI-Technologie übertrifft Bing von Microsoft Google im Suchverkehr

