Heim >Technologie-Peripheriegeräte >KI >Zusammenfassung wichtiger Wissenspunkte im Zusammenhang mit Regressionsmodellen für maschinelles Lernen
Zusammenfassung wichtiger Wissenspunkte im Zusammenhang mit Regressionsmodellen für maschinelles Lernen
- WBOYnach vorne
- 2023-04-08 19:01:041929Durchsuche
1. Was sind die Annahmen der linearen Regression?
Die lineare Regression basiert auf vier Annahmen:
- Linearität: Es sollte eine lineare Beziehung zwischen der unabhängigen Variablen (x) und der abhängigen Variablen (y) bestehen, was bedeutet, dass eine Änderung des x-Werts auch den y-Wert ändern sollte die gleiche Richtung.
- Unabhängigkeit: Features sollten unabhängig voneinander sein, was eine minimale Multikollinearität bedeutet.
- Normalität: Residuen sollten normalverteilt sein.
- Homoskedastizität: Die Varianz der Datenpunkte um die Regressionsgerade sollte für alle Werte gleich sein.
2. Was ist ein Residuum und wie wird es zur Bewertung von Regressionsmodellen verwendet?
Restfehler bezieht sich auf den Fehler zwischen dem vorhergesagten Wert und dem beobachteten Wert. Es misst den Abstand der Datenpunkte von der Regressionsgeraden. Er wird berechnet, indem vorhergesagte Werte von beobachteten Werten subtrahiert werden.
Residuendiagramme sind eine großartige Möglichkeit, Regressionsmodelle auszuwerten. Es handelt sich um ein Diagramm, das alle Residuen auf der vertikalen Achse und die Merkmale auf der x-Achse zeigt. Wenn die Datenpunkte zufällig auf Linien ohne Muster verteilt sind, passt ein lineares Regressionsmodell gut zu den Daten, andernfalls sollten wir ein nichtlineares Modell verwenden.
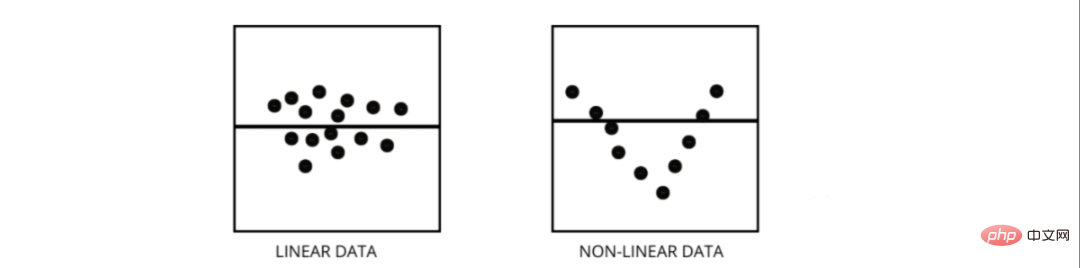
3. Wie unterscheidet man zwischen linearem Regressionsmodell und nichtlinearem Regressionsmodell?
Beide Arten von Regressionsproblemen. Der Unterschied zwischen den beiden besteht in den Daten, auf denen sie trainiert werden.
Das lineare Regressionsmodell geht von einer linearen Beziehung zwischen Merkmalen und Beschriftungen aus. Das heißt, wenn wir alle Datenpunkte nehmen und sie in einer linearen (geraden) Linie darstellen, sollte sie zu den Daten passen.
Nichtlineare Regressionsmodelle gehen davon aus, dass zwischen Variablen keine lineare Beziehung besteht. Nichtlineare (krummlinige) Linien sollten die Daten trennen und korrekt anpassen.
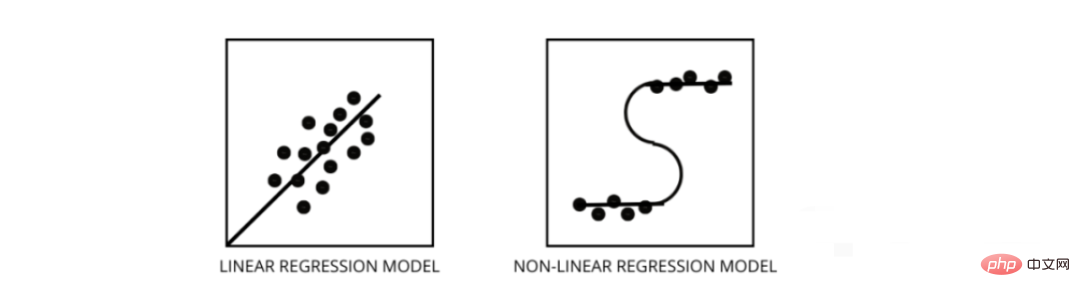
Drei beste Möglichkeiten, um herauszufinden, ob Ihre Daten linear oder nichtlinear sind –
- Residuendiagramme
- Streudiagramme
- Unter der Annahme, dass die Daten linear sind, trainieren Sie ein lineares Modell und bewerten Sie es anhand der Genauigkeit.
4. Was ist Multikollinearität und wie wirkt sie sich auf die Modellleistung aus?
Multikollinearität tritt auf, wenn bestimmte Merkmale stark miteinander korrelieren. Korrelation bezieht sich auf ein Maß, das angibt, wie eine Variable durch Änderungen einer anderen Variable beeinflusst wird.
Wenn eine Zunahme von Merkmal a zu einer Zunahme von Merkmal b führt, dann sind die beiden Merkmale positiv korreliert. Wenn eine Zunahme von a zu einer Abnahme von Merkmal b führt, sind die beiden Merkmale negativ korreliert. Das Vorhandensein zweier stark korrelierter Variablen in den Trainingsdaten führt zu Multikollinearität, da das Modell keine Muster in den Daten finden kann, was zu einer schlechten Modellleistung führt. Daher müssen wir vor dem Training des Modells zunächst versuchen, die Multikollinearität zu beseitigen.
5. Wie wirken sich Ausreißer auf die Leistung linearer Regressionsmodelle aus?
Ausreißer sind Datenpunkte, deren Werte vom durchschnittlichen Bereich der Datenpunkte abweichen. Mit anderen Worten: Diese Punkte weichen von den Daten ab oder liegen außerhalb des 3. Kriteriums.
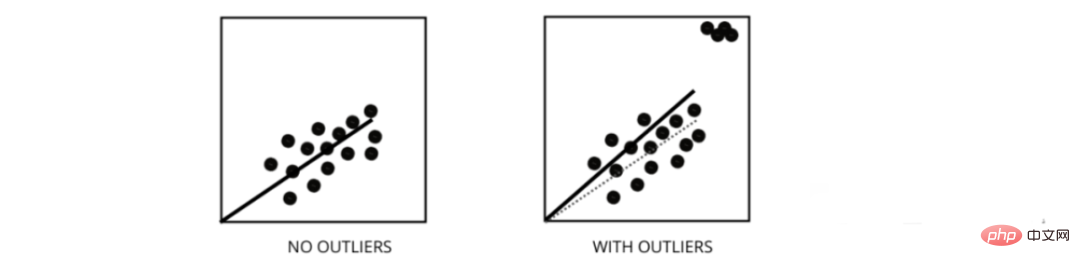
Das lineare Regressionsmodell versucht, eine am besten geeignete Linie zu finden, die die Residuen reduziert. Wenn die Daten Ausreißer enthalten, verschiebt sich die beste Anpassungslinie ein wenig in Richtung der Ausreißer, was die Fehlerrate erhöht und zu einem Modell mit einem sehr hohen MSE führt.
6. Was ist der Unterschied zwischen MSE und MAE?
MSE steht für mittlerer quadratischer Fehler, also die quadrierte Differenz zwischen dem tatsächlichen Wert und dem vorhergesagten Wert. Und MAE ist die absolute Differenz zwischen dem Zielwert und dem vorhergesagten Wert.
MSE bestraft große Fehler, MAE nicht. Wenn die Werte von MSE und MAE abnehmen, tendiert das Modell zu einer besseren Anpassungslinie.
7. Was sind L1- und L2-Regularisierungen und wann sollten sie verwendet werden?
Beim maschinellen Lernen besteht unser Hauptziel darin, ein allgemeines Modell zu erstellen, das bei Trainings- und Testdaten eine bessere Leistung erbringt. Wenn jedoch nur sehr wenige Daten vorhanden sind, neigen grundlegende lineare Regressionsmodelle zu einer Überanpassung, sodass wir die Regularisierung L1 und L2 verwenden .
L1-Regularisierung oder Lasso-Regression funktioniert durch Hinzufügen des absoluten Werts der Steigung als Strafterm innerhalb der Kostenfunktion. Hilft bei der Entfernung von Ausreißern, indem alle Datenpunkte entfernt werden, deren Steigungswerte unter einem Schwellenwert liegen.
L2-Regularisierung oder Ridge-Regression fügt einen Strafterm hinzu, der dem Quadrat der Koeffizientengröße entspricht. Es bestraft Features mit höheren Neigungswerten.
l1 und l2 sind nützlich, wenn die Trainingsdaten klein sind, die Varianz hoch ist, die vorhergesagten Merkmale größer als die beobachteten Werte sind und die Daten unter Multikollinearität leiden.
8. Was bedeutet Heteroskedastizität?
Damit ist die Situation gemeint, in der die Varianzen der Datenpunkte um die Best-Fit-Linie innerhalb eines Bereichs unterschiedlich sind. Dies führt zu einer ungleichmäßigen Verteilung der Rückstände. Wenn es in den Daten vorhanden ist, tendiert das Modell dazu, eine ungültige Ausgabe vorherzusagen. Eine der besten Möglichkeiten, die Heteroskedastizität zu testen, besteht darin, die Residuen darzustellen.
Eine der größten Ursachen für Heteroskedastizität innerhalb von Daten sind die großen Unterschiede zwischen Bereichsmerkmalen. Wenn wir beispielsweise eine Spalte von 1 bis 100.000 haben, ändert eine Erhöhung der Werte um 10 % die niedrigeren Werte nicht, führt jedoch zu einem sehr großen Unterschied bei den höheren Werten und erzeugt somit einen großen Varianzunterschied bei den Datenpunkten .
9. Welche Rolle spielt der Varianzinflationsfaktor?
Der Varianzinflationsfaktor (vif) wird verwendet, um herauszufinden, wie gut eine unabhängige Variable mithilfe anderer unabhängiger Variablen vorhergesagt werden kann.
Nehmen wir Beispieldaten mit den Funktionen v1, v2, v3, v4, v5 und v6. Um nun den Vif von v1 zu berechnen, betrachten Sie ihn als Prädiktorvariable und versuchen Sie, ihn mithilfe aller anderen Prädiktorvariablen vorherzusagen.
Wenn der Wert von VIF klein ist, ist es besser, die Variable aus den Daten zu entfernen. Denn kleinere Werte weisen auf eine hohe Korrelation zwischen Variablen hin.
10. Wie funktioniert die schrittweise Regression?
Die schrittweise Regression ist eine Methode zum Erstellen eines Regressionsmodells durch Entfernen oder Hinzufügen von Prädiktorvariablen mithilfe von Hypothesentests. Es sagt die abhängige Variable voraus, indem es iterativ die Signifikanz jeder unabhängigen Variablen testet und nach jeder Iteration einige Merkmale entfernt oder hinzufügt. Es wird n-mal ausgeführt und versucht, die beste Parameterkombination zu finden, die die abhängige Variable mit dem kleinsten Fehler zwischen den beobachteten und den vorhergesagten Werten vorhersagt.
Es kann große Datenmengen sehr effizient verwalten und hochdimensionale Probleme lösen.
11. Gibt es neben MSE und MAE noch weitere wichtige Regressionsindikatoren?

Wir verwenden ein Regressionsproblem, um diese Indikatoren einzuführen, wobei unser Input die Berufserfahrung und der Output das Gehalt ist. Die folgende Grafik zeigt eine lineare Regressionslinie zur Vorhersage des Gehalts.
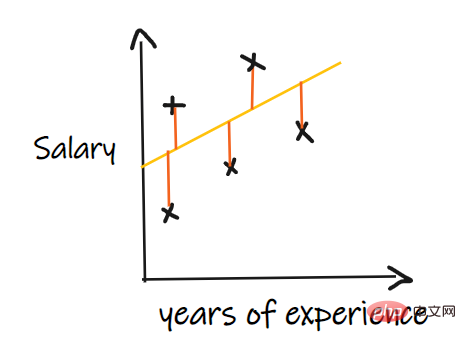
1. Mittlerer absoluter Fehler (MAE):
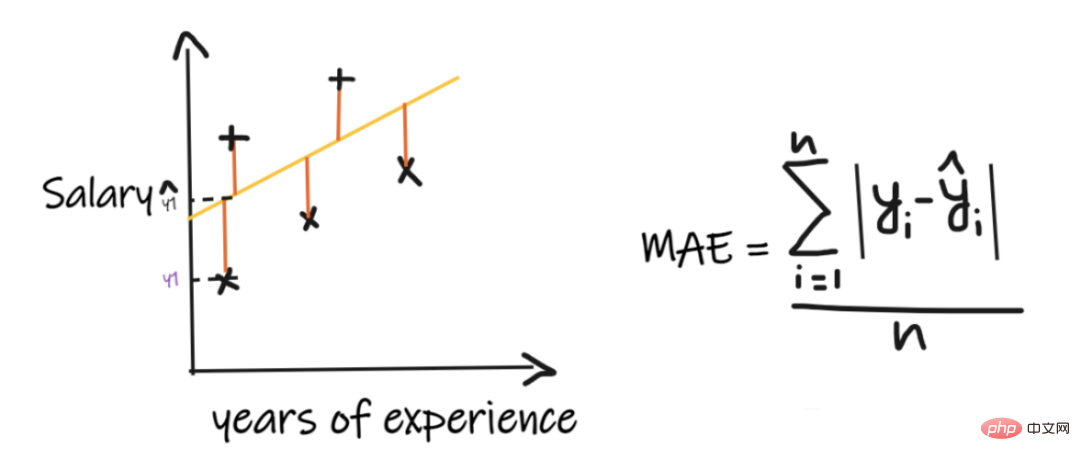
Der mittlere absolute Fehler (MAE) ist das einfachste Regressionsmaß. Es addiert die Differenz zwischen jedem tatsächlichen und vorhergesagten Wert und dividiert sie durch die Anzahl der Beobachtungen. Damit ein Regressionsmodell als gutes Modell gilt, sollte der MAE so klein wie möglich sein.
Die Vorteile von MAE sind:
Einfach und leicht verständlich. Das Ergebnis hat die gleichen Einheiten wie die Ausgabe. Beispiel: Wenn die Einheit der Ausgabespalte LPA ist und der MAE 1,2 beträgt, können wir das Ergebnis als +1,2LPA oder -1,2LPA interpretieren. MAE ist gegenüber Ausreißern relativ stabil (im Vergleich zu einigen anderen Regressionsindikatoren, MAE). wird durch Ausreißer mit geringerer Auswirkung beeinflusst). Die Nachteile von
MAE sind:
MAE verwendet eine modulare Funktion, die modulare Funktion ist jedoch nicht an allen Punkten differenzierbar und kann daher in vielen Fällen nicht als Verlustfunktion verwendet werden.
2. Mittlerer quadratischer Fehler (MSE):
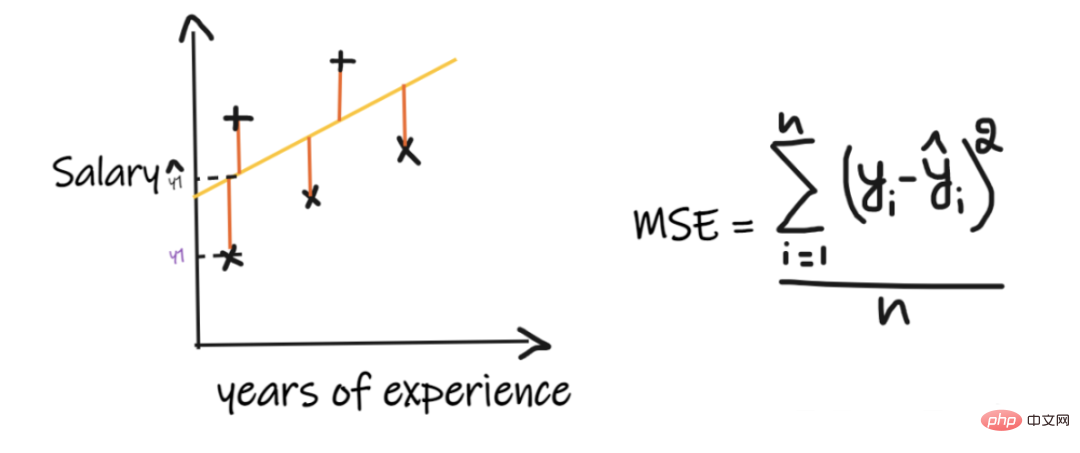
MSE nimmt die Differenz zwischen jedem tatsächlichen Wert und dem vorhergesagten Wert, quadriert dann die Differenz, addiert sie und dividiert schließlich durch die Anzahl der Beobachtungen. Damit ein Regressionsmodell als gutes Modell gilt, sollte die MSE so klein wie möglich sein.
Vorteile von MSE: Die Quadratfunktion ist an allen Punkten differenzierbar und kann daher als Verlustfunktion verwendet werden.
Nachteile von MSE: Da MSE die Quadratfunktion verwendet, ist die Einheit des Ergebnisses das Quadrat der Ausgabe. Daher ist es schwierig, die Ergebnisse zu interpretieren. Da eine Quadratfunktion verwendet wird, werden bei Ausreißern in den Daten auch die Differenzen quadriert, sodass MSE für Ausreißer nicht stabil ist.
3. Root Mean Square Error (RMSE):
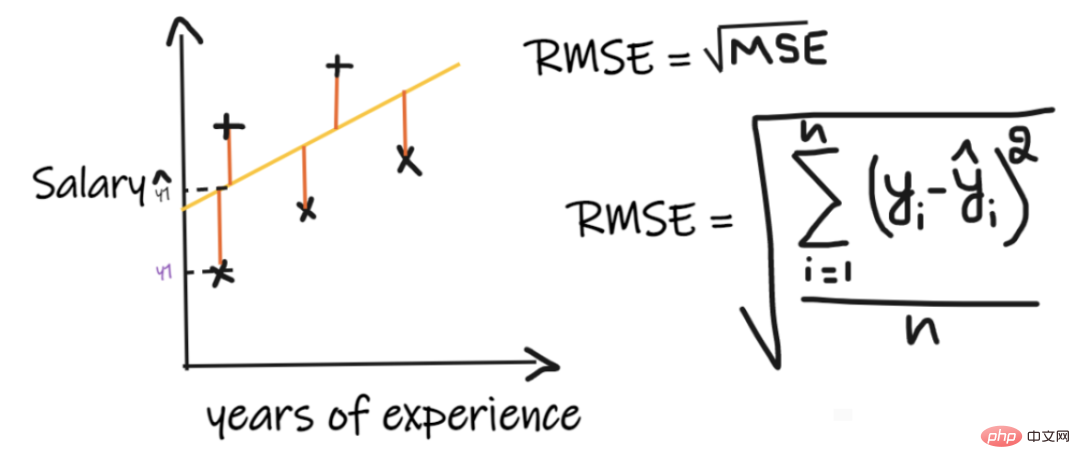
Der Root Mean Square Error (RMSE) nimmt die Differenz zwischen jedem tatsächlichen Wert und dem vorhergesagten Wert, quadriert dann die Differenz und addiert sie und dividiert schließlich durch Anzahl der Beobachtungen. Ziehen Sie dann die Quadratwurzel aus dem Ergebnis. Daher ist RMSE die Quadratwurzel von MSE. Damit ein Regressionsmodell als gutes Modell gilt, sollte der RMSE so klein wie möglich sein.
RMSE löst das Problem von MSE. Die Einheiten sind mit denen der Ausgabe identisch, da es die Quadratwurzel zieht, aber es ist immer noch weniger stabil gegenüber Ausreißern.
Die oben genannten Indikatoren hängen vom Kontext des Problems ab, das wir lösen. Wir können die Qualität des Modells nicht allein anhand der Werte von MAE, MSE und RMSE beurteilen, ohne das eigentliche Problem zu verstehen.
4, R2-Score:
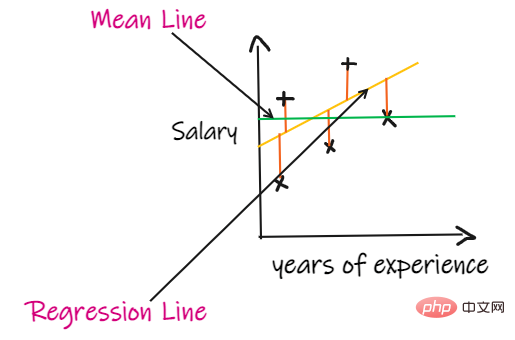
Wenn wir keine Eingabedaten haben, aber wissen wollen, wie viel Gehalt er in diesem Unternehmen bekommt, dann geben wir ihnen am besten den Durchschnitt aller Mitarbeiter ' Gehaltswert.
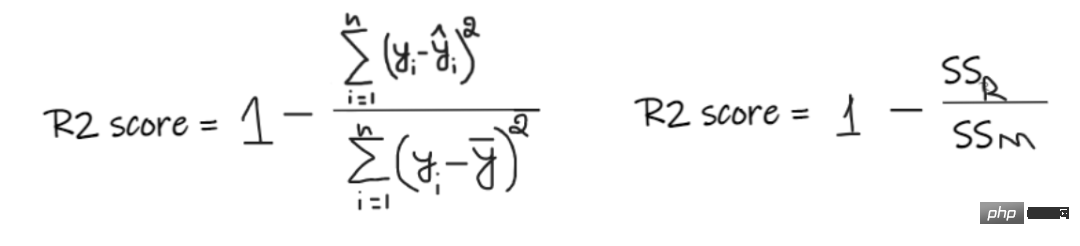
R2-Score gibt einen Wert zwischen 0 und 1 an und kann für jeden Kontext interpretiert werden. Darunter kann die Qualität der Passform verstanden werden.
SSR ist die Summe der quadratischen Fehler der Regressionsgeraden und SSM ist die Summe der quadratischen Fehler des gleitenden Durchschnitts. Wir vergleichen die Regressionsgerade mit der Mittellinie.
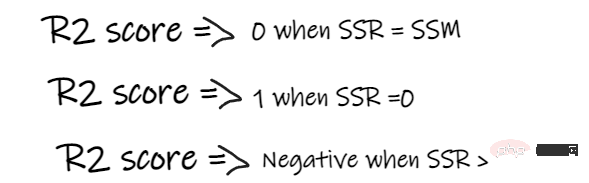
- Wenn der R2-Score 0 ist, bedeutet dies, dass unser Modell die gleichen Ergebnisse wie der Durchschnitt erzielt, sodass unser Modell verbessert werden muss.
- Wenn der R2-Score 1 ist, wird die rechte Seite der Gleichung zu 0, was nur passieren kann, wenn unser Modell an jeden Datenpunkt passt und keine Fehler macht.
- Wenn der R2-Wert negativ ist, bedeutet dies, dass die rechte Seite der Gleichung größer als 1 ist, was passieren kann, wenn SSR > SSM. Dies bedeutet, dass unser Modell schlechter ist als der Mittelwert, was bedeutet, dass unser Modell schlechter ist als die Verwendung des Mittelwerts zur Vorhersage
Wenn unser Modell einen R2-Wert von 0,8 hat, bedeutet dies, dass wir sagen können, dass das Modell in der Lage ist, zu erklären 80 % der Ausgabevarianz. Das heißt, 80 % der Lohnschwankungen können durch den Input (Arbeitsjahre) erklärt werden, die restlichen 20 % sind jedoch unbekannt.
Wenn unser Modell zwei Merkmale hat, Arbeitsjahre und Interviewergebnisse, dann kann unser Modell 80 % der Gehaltsänderungen mithilfe dieser beiden Eingabemerkmale erklären.
Nachteile von R2:
Wenn die Anzahl der Eingabemerkmale zunimmt, steigt R2 tendenziell entsprechend an oder bleibt gleich, nimmt jedoch niemals ab, selbst wenn die Eingabemerkmale für unser Modell nicht wichtig sind (z. B. durch Hinzufügen der Anzahl). der Eingabemerkmale am Tag des Interviews) Addiert man die Lufttemperatur zu unserem Beispiel, sinkt R2 nicht, selbst wenn die Temperatur für die Ausgabe nicht wichtig ist.
5. Angepasster R2-Score:
In der obigen Formel ist R2 R2, n ist die Anzahl der Beobachtungen (Zeilen) und p ist die Anzahl der unabhängigen Merkmale. Angepasstes R2 löst die Probleme von R2.
Wenn wir Funktionen hinzufügen, die für unser Modell weniger wichtig sind, wie z. B. das Hinzufügen der Temperatur zur Vorhersage des Gehalts .....

Beim Hinzufügen wichtiger Funktionen für das Modell, z. B. Hinzufügen von Interviewergebnissen zur Vorhersage des Gehalts ...

Das Obige sind die wichtigen Wissenspunkte von Regressionsproblemen und die Einführung verschiedener wichtiger Indikatoren, die zur Lösung verwendet werden Regressionsprobleme, ich hoffe, es hilft Ihnen.
Das obige ist der detaillierte Inhalt vonZusammenfassung wichtiger Wissenspunkte im Zusammenhang mit Regressionsmodellen für maschinelles Lernen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Technologietrends, die Sie im Jahr 2023 im Auge behalten sollten
- Wie künstliche Intelligenz Rechenzentrumsteams neue Alltagsaufgaben beschert
- Können künstliche Intelligenz oder Automatisierung das Problem der geringen Energieeffizienz in Gebäuden lösen?
- OpenAI-Mitbegründer im Interview mit Huang Renxun: Die Argumentationsfähigkeiten von GPT-4 haben noch nicht die Erwartungen erfüllt
- Dank der OpenAI-Technologie übertrifft Bing von Microsoft Google im Suchverkehr

