Erneute Untersuchung der KI, der Entdeckung und des Proof-of-Concept-Symbolauftritts in neuronalen Netzen

Dieser Artikel konzentriert sich auf zwei aktuelle Arbeiten, um die Entstehung symbolischer Konzepte in neuronalen Netzen zu diskutieren, also die Frage: „Ob die Darstellung tiefer neuronaler Netze symbolisch ist?“ Wenn wir die Perspektive der „Verbesserung der Anwendungstechnologie“ außer Acht lassen und KI aus der Perspektive der „wissenschaftlichen Entwicklung“ erneut untersuchen, ist es zweifellos von großer Bedeutung zu beweisen, dass das Phänomen der Symbolentstehung in KI-Modellen von großer Bedeutung ist.

1 Zunächst einmal versucht der Großteil der aktuellen Interpretierbarkeitsforschung, neuronale Netze als „klares“, „semantisches“ oder „logisches“ Modell zu interpretieren. Wenn jedoch die symbolische Entstehung neuronaler Netze nicht nachgewiesen werden kann und die intrinsischen Repräsentationskomponenten neuronaler Netze tatsächlich viele chaotische Komponenten aufweisen, verlieren die meisten Interpretationsforschungen ihre grundlegende Faktenbasis.

2. Wenn die symbolische Entstehung neuronaler Netze nicht nachgewiesen werden kann, wird die Entwicklung von Deep Learning höchstwahrscheinlich auf der Ebene peripherer Faktoren wie „Struktur“, „Verlustfunktion“, „Daten“ stecken bleiben. usw. und ist nicht in der Lage, die kognitive Ebene auf hohem Niveau direkt zu analysieren, um interaktives Lernen auf der Wissensebene zu erreichen. Eine Entwicklung in diese Richtung erfordert eine klarere und klarere theoretische Unterstützung.

Daher stellt dieser Artikel es hauptsächlich unter den folgenden drei Aspekten vor.

1. Wie man das durch neuronale Netze modellierte symbolische Konzept definiert, um das symbolische Emergenzphänomen neuronaler Netze zuverlässig zu entdecken.

2. Warum die quantifizierten symbolischen Konzepte als glaubwürdige Konzepte angesehen werden können (Sparsamkeit, universelle Übereinstimmung neuronaler Netzwerkdarstellungen, Übertragbarkeit, Klassifizierung, Interpretation historischer Erklärungsindikatoren).

3. Wie man die Entstehung symbolischer Konzepte beweist – das heißt, theoretisch beweisen, dass die Darstellungslogik des KI-Modells unter bestimmten Umständen (nicht harten Bedingungen) dekonstruiert werden kann in eine sehr kleine Anzahl übertragbarer Symbole. Der Klassifizierungsnutzen des Transformationsbegriffs (dieser Teil wird Ende April öffentlich diskutiert).

Papieradresse: https://arxiv.org/pdf/2111.06206.pdf

Papieradresse: https://arxiv.org /pdf/ 2302.13080.pdf

Zu den Autoren der Studie gehören Li Mingjie, ein Masterstudent im zweiten Jahr an der Shanghai Jiao Tong University, und Ren Jie, ein Doktorand im dritten Jahr an der Shanghai Jiao Tong University, sowohl Li Mingjie als auch Ren Jie studierte bei Zhang Quanshi. Ihr Laborteam forscht das ganze Jahr über an der Interpretierbarkeit neuronaler Netze. Für den Bereich der Interpretierbarkeit können Forscher ihn aus verschiedenen Blickwinkeln analysieren, einschließlich der Erklärung der Darstellung, der Erklärung der Leistung, relativ zuverlässig und vernünftig und einiger unvernünftiger. Wenn wir jedoch weiter diskutieren, gibt es zwei grundlegende Visionen für die Erklärung neuronaler Netze, nämlich „Kann die durch neuronale Netze modellierten Konzepte klar und genau darstellen“ und „Kann es genau erklärt werden? Finden.“ Finden Sie die Faktoren heraus, die die Leistung neuronaler Netze bestimmen“.

In der Richtung „Erklärung der durch neuronale Netze modellierten Konzepte“ gibt es eine Kernfrage, der sich alle Forscher stellen müssen: „Ist die Darstellung neuronaler Netze symbolisch konzeptionell?“. Wenn die Antwort auf diese Frage unklar ist, wird es schwierig sein, nachfolgende Forschungen durchzuführen – wenn die Darstellung des neuronalen Netzwerks selbst chaotisch ist und der Forscher dann eine Reihe von „symbolischen Konzepten“ oder „kausalen Logiken“ zur Erklärung zwingt, Dies wird der Fall sein. Sind Sie in die falsche Richtung gekommen? Die Annahme einer symbolischen Darstellung neuronaler Netze ist die Grundlage für eingehende Forschung auf diesem Gebiet, aber die Demonstration dieses Problems macht es den Menschen oft unmöglich, damit anzufangen.

Der erste Instinkt der meisten Forscher zu neuronalen Netzen ist: „Das kann doch nicht symbolisch sein, oder?“ Neuronale Netze sind doch keine grafischen Modelle. In einem von Cynthia et al. verfassten Artikel „Hören Sie auf, Black-Box-Modelle für maschinelles Lernen für Entscheidungen mit hohem Einsatz zu erklären, und verwenden Sie stattdessen interpretierbare Modelle“ [3] wird fälschlicherweise davon ausgegangen, dass es sich bei den Menschen um post-hoc-Erklärungen neuronaler Netze handelt, die von Natur aus unzuverlässig sind .

Die intrinsische Darstellung neuronaler Netze ist also wirklich sehr verwirrend? Anstatt klar, spärlich und symbolisch? Wir konzentrierten uns auf dieses Problem, definierten die Spielinteraktion [4, 5], bewiesen den Engpass der Darstellung neuronaler Netze [6] und untersuchten die Merkmale der Darstellung visueller Konzepte durch neuronale Netze [7, 8] und bewiesen damit, dass es sich um ein Interaktionskonzept handelt Die Beziehung zwischen Transformation und Robustheit ist eng mit dem neuronalen Netzwerk verbunden [9,10,11,12] und der Shapley-Wert wurde verbessert [13]. Die Peripherie des Kerns der „symbolischen Darstellung“ und konnte sie nicht direkt erforschen Ob die neuronale Netzwerkdarstellung symbolisch ist.

Hier beginnen wir mit der Schlussfolgerung – In den meisten Fällen ist die Darstellung neuronaler Netze klar, spärlich und symbolisch. Hinter dieser Schlussfolgerung stecken viele theoretische Beweise und viele experimentelle Demonstrationen. In theoretischer Hinsicht hat unsere aktuelle Forschung einige Eigenschaften nachgewiesen, die eine „Symbolisierung“ unterstützen können, aber der aktuelle Beweis reicht nicht aus, um eine strenge und klare Antwort auf die „Symbolisierungsdarstellung“ zu geben. In den nächsten Monaten werden wir strengere und umfassendere Beweise haben.

Wie definiert man das vom neuronalen Netzwerk modellierte Konzept?

Bevor wir das neuronale Netzwerk analysieren, müssen wir klären, „wie das vom Netzwerk modellierte Konzept zu definieren ist“. Tatsächlich gab es zu diesem Thema schon früher relevante Studien [14,15], und die experimentellen Ergebnisse sind relativ ausgezeichnet. Wir glauben jedoch, dass die Definition von „Konzept“ theoretisch „streng“ sein sollte . Daher haben wir im Artikel [1] den Index I(S)

definiert, um den Nutzen des Konzepts S für die Netzwerkausgabe zu quantifizieren, wobei sich S auf alle Eingabevariablen bezieht, aus denen sich dieses Konzept zusammensetzt. Wenn beispielsweise ein neuronales Netzwerk und ein Eingabesatz x = „Ich denke, er ist eine grüne Hand.“ gegeben sind, kann jedes Wort als eine der Eingabevariablen des Netzwerks betrachtet werden, und die drei Wörter „a“ und „grün“ Im Satz kann „Hand“ einen potentiellen Begriff S={a, green, hand} darstellen. Jedes Konzept S stellt die „UND“-Beziehung zwischen

Eingabevariablen in S dar: Dieses Konzept wird nur dann ausgelöst, wenn alle Eingabevariablen in S erscheinen, und trägt so zum Nutzen des Netzwerkausgangs I (S) bei. Wenn eine Variable in S verdeckt wird, wird der Nutzen von I (S) aus der ursprünglichen Netzwerkausgabe entfernt. Wenn beispielsweise für das Konzept S={a, green, hand} das Wort „Hand“ im Eingabesatz blockiert ist, wird dieses Konzept nicht ausgelöst und die Netzwerkausgabe enthält nicht den Nutzen dieses Konzepts. IST).

Wir haben bewiesen, dass die Ausgabe des neuronalen Netzwerks immer in die Summe der Nutzen aller ausgelösten Konzepte aufgeteilt werden kann. Das heißt, theoretisch gibt es für eine Stichprobe mit n Eingabeeinheiten höchstens

verschiedene Okklusionsmethoden. Wir können immer den Nutzen einer „kleinen Anzahl von Konzepten“ nutzen, um „genau“ zu ermitteln fit“ das neuronale Netzwerk „Alle

Typen“ gibt Werte an verschiedenen Okklusionsproben aus und beweist so die „Strenge“ von I(S)

. Die folgende Abbildung zeigt ein einfaches Beispiel.

Darüber hinaus haben wir in der Arbeit [1] bewiesen, dass I (S) 7 Eigenschaften in der Spieltheorie erfüllt, was die Zuverlässigkeit dieses Indikators weiter verdeutlicht.

Darüber hinaus haben wir auch bewiesen, dass das Spielinteraktionskonzept I (S) den Grundmechanismus einer großen Anzahl klassischer Indikatoren in der Spieltheorie erklären kann, wie z. B. Shapley-Wert [16], Shapley-Interaktionsindex [17] und Shapley -Taylor-Interaktionsindex [18]. Konkret können wir diese drei Indikatoren als Formen verschiedener linearer Interaktionssummenkonzepte darstellen.

Tatsächlich hat das Forschungsteam in seiner Vorarbeit den optimalen Benchmarkwert des Shapley-Werts basierend auf dem Game Interaction Concept Index [13] definiert und das vom visuellen neuronalen Netzwerk modellierte „prototypische visuelle Konzept“ untersucht und seine „Ästhetik“[8].

Ist das Modell des neuronalen Netzwerks klare, symbolische konzeptionelle Darstellungen?

Mit diesem Indikator gehen wir der oben genannten Kernfrage weiter nach: Kann das neuronale Netzwerk wirklich klare, symbolische Darstellungen aus den Trainingsaufgaben zusammenfassen? Symbolische, konzeptionelle Darstellung? Kann das definierte Interaktionskonzept wirklich sinnvolles „Wissen“ darstellen, oder handelt es sich nur um eine knifflige Metrik, die rein aus der Mathematik stammt und keine klare Bedeutung hat? Zu diesem Zweck beantworten wir diese Frage unter den folgenden vier Aspekten: Die Darstellung der symbolischen Konzeptualisierung sollte Sparsamkeit, Übertragbarkeit zwischen Stichproben, Übertragbarkeit zwischen Netzwerken und Klassifizierung erfüllen.

Anforderung 1 (Konzeptsparsität): Die vom neuronalen Netzwerk modellierten Konzepte sollten spärlich sein vom Netzwerk erlerntes Wissen, anstatt eine große Anzahl dichter Konzepte zu verwenden. In Experimenten haben wir herausgefunden, dass es unter einer großen Anzahl potenzieller Konzepte nur eine sehr kleine Anzahl hervorstechender Konzepte gibt. Das heißt, der Interaktionsnutzen I (S) der meisten interaktiven Konzepte nähert sich 0, sodass nur eine sehr kleine Anzahl interaktiver Konzepte einen signifikanten Interaktionsnutzen I (S) aufweisen hängt nur vom Interaktionsnutzen einer kleinen Anzahl von Konzepten ab. Mit anderen Worten: Die Schlussfolgerung des neuronalen Netzwerks für jede Stichprobe kann kurz und bündig als der Nutzen einer kleinen Anzahl hervorstechender Konzepte erklärt werden.

Anforderung 2 (Übertragbarkeit zwischen Proben): Das vom neuronalen Netzwerk modellierte Konzept sollte zwischen verschiedenen Proben übertragbar sein

Es reicht bei weitem nicht aus, um die Sparsität einer einzelnen Probe zu erfüllen. Diese spärlichen Konzeptausdrücke sollten zwischen verschiedenen Stichproben übertragbar sein. Wenn dasselbe Interaktionskonzept in verschiedenen Stichproben dargestellt werden kann und verschiedene Stichproben immer ähnliche Interaktionskonzepte extrahieren, ist es wahrscheinlicher, dass dieses Interaktionskonzept ein sinnvolles und universelles Wissen darstellt. Im Gegenteil, wenn die meisten Interaktionskonzepte nur auf einer oder zwei spezifischen Stichproben dargestellt werden, ist es wahrscheinlicher, dass die auf diese Weise definierte Interaktion eine knifflige Metrik mit nur mathematischen Definitionen, aber keiner physikalischen Bedeutung ist. In Experimenten haben wir herausgefunden, dass es oft ein kleineres Konzeptwörterbuch gibt, das die meisten Konzepte erklären kann, die von neuronalen Netzen für Stichproben derselben Kategorie modelliert werden.

Wir haben auch einige Konzepte visualisiert und festgestellt, dass das gleiche Konzept normalerweise ähnliche Effekte auf verschiedene Stichproben hervorruft, was auch die Übertragbarkeit von Konzepten zwischen verschiedenen Stichproben bestätigt.

Anforderung drei (Übertragbarkeit zwischen Netzwerken): Es sollte eine Übertragbarkeit zwischen Konzepten bestehen, die von verschiedenen neuronalen Netzwerken modelliert werden

In ähnlicher Weise sollten diese Konzepte von verschiedenen neuronalen Netzen stabil erlernt werden können, unabhängig davon, ob es sich um Netze mit unterschiedlicher Initialisierung oder unterschiedlicher Architektur handelt. Obwohl neuronale Netze mit völlig unterschiedlichen Architekturen und Modellmerkmalen unterschiedlicher Dimensionen entworfen werden können, können unterschiedliche neuronale Netze, wenn sie vor derselben spezifischen Aufgabe stehen, „dasselbe Ziel auf unterschiedlichen Wegen“ erreichen, d. h. wenn unterschiedliche neuronale Netze stabil ähnlich lernen können Wenn es sich um eine Reihe von Interaktionskonzepten handelt, können wir davon ausgehen, dass diese Reihe von Interaktionskonzepten die grundlegende Darstellung dieser Aufgabe darstellt. Wenn beispielsweise verschiedene Gesichtserkennungsnetzwerke alle die Interaktion zwischen Augen, Nase und Mund modellieren, können wir davon ausgehen, dass eine solche Interaktion „wesentlicher“ und „zuverlässiger“ ist. In Experimenten haben wir herausgefunden, dass die hervorstechenderen Konzepte von verschiedenen Netzwerken gleichzeitig leichter erlernt werden können und der relative Anteil hervorstechender Interaktionen von verschiedenen neuronalen Netzwerken gemeinsam modelliert wird.

Anforderung 4 (Konzeptklassifizierung): Das vom neuronalen Netzwerk modellierte Konzept sollte klassifizierbar sein

Wenn ein Konzept bei Klassifizierungsaufgaben schließlich eine hohe Klassifizierung aufweist, sollte es ein konsistent positives Ergebnis haben Auswirkung (oder eine konsistente negative Auswirkung) auf die Klassifizierung der meisten Proben. Eine höhere Klassifizierbarkeit kann bestätigen, dass das Konzept die Klassifizierungsaufgabe unabhängig durchführen kann, wodurch es wahrscheinlicher ist, dass es sich um ein zuverlässiges Konzept und nicht um ein unausgereiftes Zwischenmerkmal handelt. Wir haben auch Experimente entworfen, um diese Eigenschaft zu überprüfen, und festgestellt, dass durch neuronale Netze modellierte Konzepte tendenziell höhere Klassifizierungseigenschaften aufweisen.

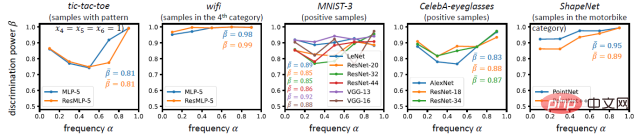
Zusammenfassend zeigen die oben genannten vier Aspekte, dass die Darstellung neuronaler Netze in den meisten Fällen klar, spärlich und symbolisch ist. Natürlich sind neuronale Netze nicht immer in der Lage, solch klare und symbolische Konzepte zu modellieren. In einigen extremen Fällen können neuronale Netze spärliche und übertragbare Konzepte nicht lernen. Weitere Informationen finden Sie in unserem Artikel [2].

Darüber hinaus nutzen wir diese Interaktion, um große Modelle zu erklären [22].

Die Bedeutung der symbolischen Darstellung neuronaler Netze für die Interpretierbarkeit neuronaler Netze

1 Aus Sicht der Entwicklung des Bereichs der Interpretierbarkeit besteht die direkteste Bedeutung darin, eine bestimmte Grundlage für die „Erklärung neuronaler Netze“ zu finden auf der konzeptionellen Ebene“ basiert. Wenn die Darstellung des neuronalen Netzwerks selbst nicht symbolisch ist, kann die Erklärung des neuronalen Netzwerks auf der symbolischen konzeptionellen Ebene nur an der Oberfläche kratzen. Die Ergebnisse der Erklärung müssen fadenscheinig sein und können keine substanziellen Rückschlüsse auf die Weiterentwicklung des Deep Learning ziehen.

2. Ab 2021 werden wir schrittweise ein theoretisches System aufbauen, das auf Spielinteraktion basiert. Es zeigt sich, dass wir auf der Grundlage der Spielinteraktion zwei Kernthemen einheitlich erklären können: „Wie lässt sich das durch neuronale Netze modellierte Wissen quantifizieren“ und „Wie lässt sich die Darstellungsfähigkeit neuronaler Netze erklären“. In Richtung „Wie kann man das durch neuronale Netze modellierte Wissen quantifizieren“? Zusätzlich zu den beiden in diesem Artikel erwähnten Arbeiten basierte die Vorarbeit des Forschungsteams auf Indikatoren für Spielinteraktionskonzepte, um den optimalen Benchmarkwert des Shapley-Werts zu definieren [ 13] und erforschen Sie das „prototypische visuelle Konzept“ und seine „Ästhetik“, modelliert durch das visuelle neuronale Netzwerk [7,8].

3. In der Richtung „Wie lässt sich die Darstellungsfähigkeit neuronaler Netze erklären“ bewies das Forschungsteam den Engpass neuronaler Netze bei der Darstellung verschiedener Interaktionen [6] und untersuchte, wie neuronale Netze die Darstellungsfähigkeit neuronaler Netze bestimmen Seine Verallgemeinerung [12, 19], die die Beziehung zwischen den von neuronalen Netzen modellierten interaktiven Konzepten und ihrer kontradiktorischen Robustheit und kontradiktorischen Übertragbarkeit [9, 10, 11, 20] untersucht, beweist, dass Bayes'sche neuronale Netze es sind schwieriger zu erstellen. Komplexe Interaktionskonzepte modellieren [21].

Weitere Informationen finden Sie unter:

​https://zhuanlan.zhihu.com/p/264871522/​

Das obige ist der detaillierte Inhalt vonErneute Untersuchung der KI, der Entdeckung und des Proof-of-Concept-Symbolauftritts in neuronalen Netzen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!