Detaillierte Erläuterung der Entscheidungsplanungstechnologie für autonomes Fahren

Mit der rasanten Entwicklung der Deep-Reinforcement-Learning-Technologie haben immer mehr Forschungsteams damit begonnen, diese auf die autonome Fahrentscheidungsplanung anzuwenden und Module zur Verhaltensentscheidung und Bewegungsplanung zu integrieren, um Fahrtrajektorien direkt zu lernen.

Das Entscheidungsplanungsmodul beim autonomen Fahren ist einer der Kernindikatoren für die Messung und Bewertung der autonomen Fahrfähigkeiten. Seine Hauptaufgabe besteht darin, die aktuelle Umgebung nach Erhalt verschiedener sensorischer Informationen von Sensoren zu analysieren und dann das zugrunde liegende Steuermodul zu steuern Bestellungen. Ein typisches Entscheidungsplanungsmodul kann in drei Ebenen unterteilt werden: globale Pfadplanung, Verhaltensentscheidung und Bewegungsplanung.

01 Einführung

Wenn in einem vollständigen autonomen Fahrsystem das Wahrnehmungsmodul mit menschlichen Augen und Ohren verglichen wird, dann ist die Entscheidungsplanung das Gehirn des autonomen Fahrens. Nachdem das Gehirn verschiedene sensorische Informationen vom Sensor erhalten hat, analysiert es die aktuelle Umgebung und gibt dann Anweisungen an das zugrunde liegende Steuerungsmodul. Dieser Prozess ist die Hauptaufgabe des Entscheidungs- und Planungsmoduls. Gleichzeitig ist die Bewältigung komplexer Szenarien durch das Entscheidungsplanungsmodul auch einer der Kernindikatoren für die Messung und Bewertung autonomer Fahrfähigkeiten [1].

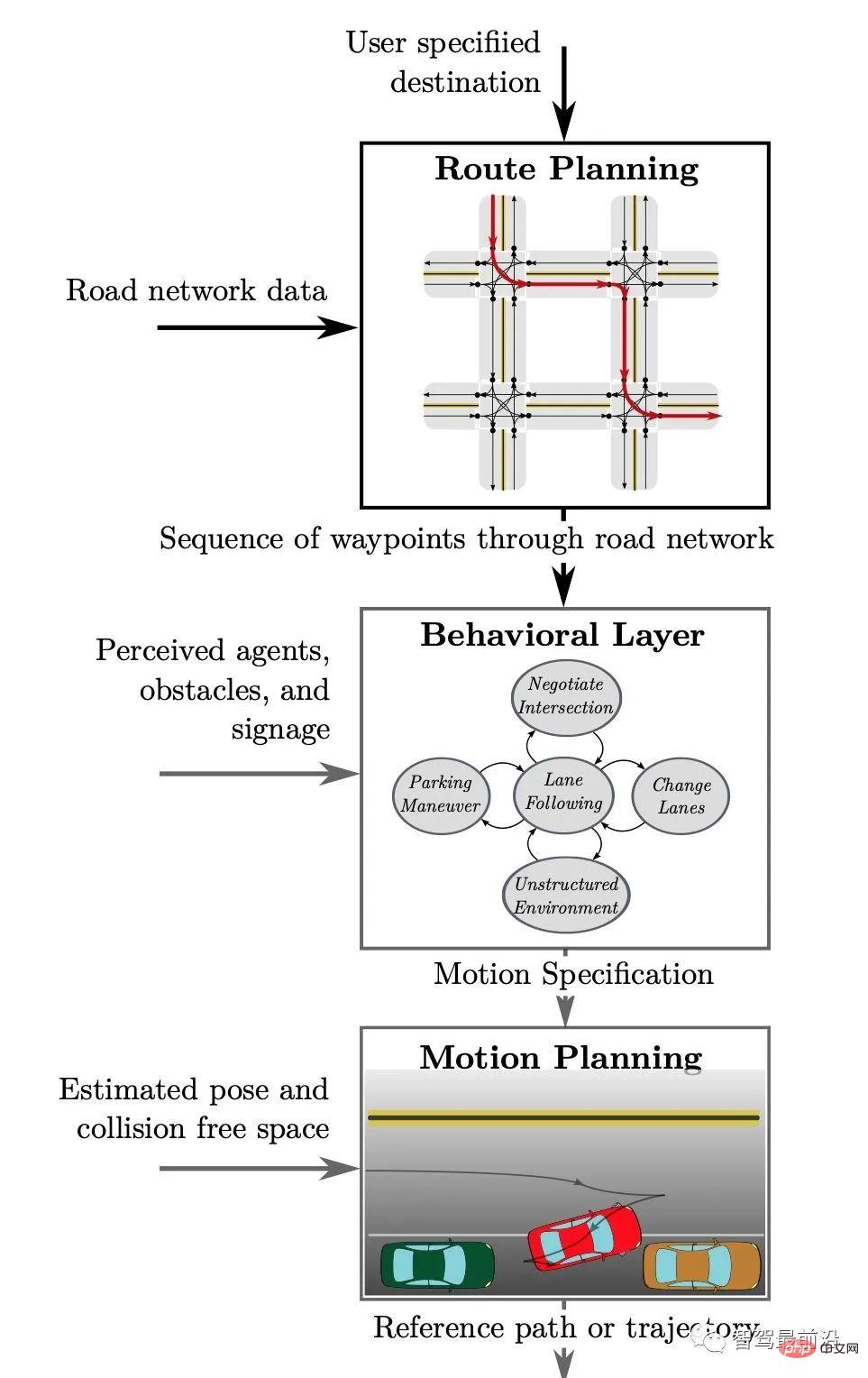
Abbildung 1. Die hierarchische Struktur des Entscheidungsplanungsmoduls im autonomen Fahrsystem, zitiert aus [2]

Wie in Abbildung 1 dargestellt, kann ein typisches Entscheidungsplanungsmodul in drei Ebenen unterteilt werden .

Unter anderem kombiniert die globale Routenplanung (Routenplanung) nach Erhalt eines bestimmten Fahrziels die Karteninformationen, um eine globale Route als Referenz für die nachfolgende spezifische Routenplanung zu generieren.

Verhaltensebene) Nach Erhalt des globalen Pfades kombinieren die vom Wahrnehmungsmodul erhaltenen Umgebungsinformationen (einschließlich anderer Fahrzeuge und Fußgänger, Hindernisse und Verkehrsregeln auf der Straße), um spezifische Verhaltensentscheidungen zu treffen (z. B. die Wahl, die Spur zu wechseln, um zu überholen oder zu folgen);

Abschließend die Bewegungsplanung Die Ebene plant die Generierung einer Trajektorie, die bestimmte Einschränkungen (z. B. die eigenen dynamischen Einschränkungen des Fahrzeugs, Kollisionsvermeidung, Fahrgastkomfort usw.) erfüllt, basierend auf bestimmten Verhaltensentscheidungen. Diese Trajektorie dient als Eingabe für das Steuermodul und bestimmt den endgültigen Fahrweg des Fahrzeugs.

In diesem Artikel werden die Hauptfunktionen und allgemeinen Algorithmen jeder Schicht vorgestellt und die Vor- und Nachteile verschiedener Algorithmen und anwendbarer Szenarien verglichen.

02 Globale Pfadplanung (Routenplanung)

Globale Pfadplanung bezieht sich auf die Auswahl eines optimalen Pfades durch Suche nach gegebener aktueller Position des Fahrzeugs und des Endziels. Das „optimale“ umfasst hier den kürzesten Pfad oder die Ankunftszeit. Schnellste und andere Bedingungen. Dieser Vorgang ähnelt der „Navigations“-Funktion, die wir häufig in unserem Leben verwenden. Der Unterschied besteht darin, dass die beim autonomen Fahren verwendete hochpräzise Karte mehr Informationen über jede Spur enthält Information. Zu den gängigen globalen Pfadplanungsalgorithmen gehören Dijkstra- und A-Algorithmen sowie verschiedene Verbesserungen, die auf diesen beiden Algorithmen basieren. Der Dijkstra-Algorithmus [3] und der A*-Algorithmus [4] sind auch die beiden am häufigsten verwendeten Suchalgorithmen bei vielen Planungsproblemen.

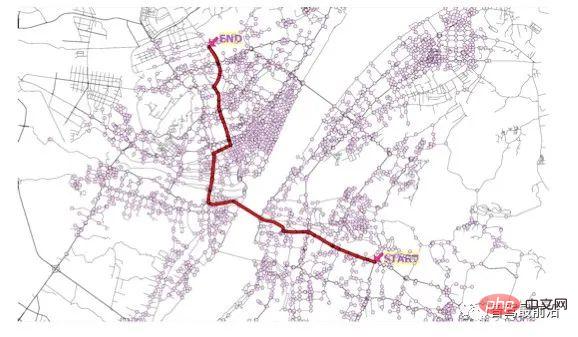
Abbildung 2. Schema der globalen Pfadplanung

1. Dijkstra-Algorithmus

Der Dijkstra-Algorithmus wurde 1956 vom Informatiker Edsger W. Dijkstra vorgeschlagen, um den kürzesten Pfad zwischen Knoten in einem Diagramm zu finden. Im Dijkstra-Algorithmus müssen die Gesamtbewegungskosten jedes Knotens vom Startpunkt aus berechnet werden. Gleichzeitig ist auch eine Prioritätswarteschlangenstruktur erforderlich. Alle zu durchlaufenden Knoten werden nach Kosten sortiert, wenn sie in die Prioritätswarteschlange gestellt werden. Während der Ausführung des Algorithmus wird jedes Mal der Knoten mit den geringsten Kosten aus der Prioritätswarteschlange als nächster durchlaufener Knoten ausgewählt. bis du das Ende erreichst.

Der Vorteil des Dijkstra-Algorithmus besteht darin, dass der gegebene Pfad optimal ist. Der Nachteil besteht darin, dass die Komplexität der Berechnungszeit relativ hoch ist (O(N2)), da er die Umgebung ohne klare Richtung erkundet.

2. A*-Algorithmus

Um das Sucheffizienzproblem des Dijkstra-Algorithmus zu lösen, wurde der A-Algorithmus 1968 von Peter Hart, Nils Nilsson und Bertram Raphael vom Stanford Research Institute veröffentlicht Verwenden Sie eine heuristische Funktion, um den Suchprozess zu steuern. Konkret berechnet Algorithmus A die Priorität jedes Knotens durch die folgende Funktion:

f(n)=g(n)+h(n)

wobei:

• f(n) ist die Gesamtpriorität von Knoten n. Wenn wir den nächsten zu durchquerenden Knoten auswählen, wählen wir immer den Knoten mit der höchsten Gesamtpriorität (Mindestwert) aus.
• g(n) sind die Kosten von Knoten n vom Startpunkt aus.
• h(n) sind die geschätzten Kosten von Knoten n vom Endpunkt, was die heuristische Funktion des A*-Algorithmus ist.

03 Verhaltensebene

Nach der Bestimmung des globalen Pfads muss das autonome Fahrzeug geeignete Verhaltensentscheidungen treffen, die auf bestimmten Straßenbedingungen, Verkehrsregeln, anderen Fahrzeugen und Fußgängern basieren.

Dieser Prozess steht vor drei Hauptproblemen:

Erstens ändern sich die realen Fahrszenen ständig. Wie kann man sie abdecken?

Zweitens ist die reale Fahrszene eine Entscheidungsumgebung mit mehreren Agenten. Das Verhalten jedes Teilnehmers, einschließlich des Hauptfahrzeugs, hat Auswirkungen auf andere Teilnehmer in der Umgebung, daher müssen wir das Verhalten anderer Teilnehmer vorhersagen

Schließlich ist es für autonome Fahrzeuge unmöglich, Umgebungsinformationen zu 100 % wahrzunehmen. Beispielsweise gibt es viele mögliche Gefahrensituationen, die durch Hindernisse blockiert werden.

Basierend auf den oben genannten Punkten müssen wir in der Entscheidungsebene zum autonomen Fahrverhalten das Planungsproblem der Wahrnehmungsunsicherheit in der komplexen Umgebung der Entscheidungsfindung mit mehreren Agenten lösen. Man kann sagen, dass dieses Problem einer der Hauptengpässe bei der tatsächlichen Verwirklichung autonomer Fahrtechnologien auf L4- und L5-Niveau ist. In den letzten Jahren wurden mit der rasanten Entwicklung von Deep Reinforcement Learning und anderen Bereichen neue Ideen und Ansätze zur Lösung dieses Problems hervorgebracht Problem.

Die Modelle der Verhaltensentscheidungsschicht sind in vier Kategorien unterteilt und werden im Folgenden separat vorgestellt [5]:

1. Finite-State-Machine-Modell

Das anfängliche Entscheidungsmodell autonomer Fahrzeuge ist der Finite-State-Machine Modell [6] Das Fahrzeug basiert auf der Auswahl geeigneter Fahrverhaltensweisen in der aktuellen Umgebung, wie z. B. Einparken, Spurwechsel, Überholen, Ausweichen, langsames Fahren usw. Das Zustandsmaschinenmodell beschreibt verschiedene Fahrzustände und die Übertragungsbeziehungen zwischen Zuständen Erstellen eines begrenzten gerichteten verbundenen Diagramms, wodurch entsprechend dem Übergang des Fahrzustands reaktiv Fahraktionen erzeugt werden.

Das Finite-State-Machine-Modell ist aufgrund seiner Einfachheit und einfachen Implementierung derzeit das am weitesten verbreitete Verhaltensentscheidungsmodell. Darüber hinaus ignoriert dieser Modelltyp die Dynamik und Unsicherheit der Umgebung. Wenn die Fahrszene viele Merkmale aufweist, ist der Staat Die Aufteilung und Verwaltung ist relativ umständlich, meist für einfache Szenarien geeignet und es ist schwierig, Verhaltensentscheidungsaufgaben in städtischen Straßenumgebungen mit umfangreichen Strukturmerkmalen durchzuführen.

2. Entscheidungsbaummodell

Das Entscheidungs-/Verhaltensbaummodell [7] ähnelt dem Zustandsmaschinenmodell. Es wählt auch verschiedene Fahraktionen reaktiv über die Attributwerte des aktuellen Fahrzustands aus Der Unterschied besteht darin, dass bei dieser Art von Modell der Fahrstatus und die Steuerlogik in einer Baumstruktur zusammengefasst werden und die Suche nach Fahrstrategien über einen Top-Down-Abfragemechanismus durchgeführt wird. Diese Art von Entscheidungsmodell verfügt über eine visuelle Steuerlogik und die Steuerknoten können wiederverwendet werden, es muss jedoch das Entscheidungsnetzwerk für jedes Fahrszenario offline definiert werden. Wenn der Zustandsraum und der Verhaltensraum groß sind, ist die Steuerlogik erforderlich komplexer sein. Darüber hinaus ist ein solches Modell auch nicht in der Lage, die im Verkehrsumfeld vorhandenen Unsicherheitsfaktoren zu berücksichtigen.

3. Wissensbasiertes Argumentations- und Entscheidungsmodell

Das wissensbasierte Argumentations- und Entscheidungsmodell imitiert den Verhaltensentscheidungsprozess menschlicher Fahrer durch die Abbildung der Beziehung zwischen „Szenenmerkmalen und Fahraktionen“. Diese Art von Modell speichert Fahrwissen im Wissen. In einer Bibliothek oder einem neuronalen Netzwerk wird das Fahrwissen hier hauptsächlich durch die Zuordnungsbeziehung zwischen Regeln, Fällen oder Szenenmerkmalen zu Fahraktionen dargestellt. Anschließend werden durch den „Abfrage“-Mechanismus treibende Maßnahmen aus der Wissensbasis oder der trainierten Netzwerkstruktur abgeleitet.

Dieser Modelltyp umfasst hauptsächlich: regelbasiertes Argumentationssystem [8], fallbasiertes Argumentationssystem [9] und auf einem neuronalen Netzwerk basierendes Zuordnungsmodell [10].

Diese Art von Modell stützt sich stark auf vorherige Fahrkenntnisse und Trainingsdaten und erfordert eine sorgfältige Organisation, Verwaltung und Aktualisierung des Fahrwissens. Obwohl das auf neuronalen Netzen basierende Zuordnungsmodell den Prozess der Datenannotation und Wissensintegration einsparen kann, gibt es solche noch die folgenden Mängel:

• Aufgrund seines „datengesteuerten“ Mechanismus ist es stark von Trainingsdaten abhängig, und die Trainingsdaten müssen ausreichend sein [11]
• Die Zuordnungsbeziehung ist in der Netzwerkstruktur verankert und ihre Interpretierbarkeit ist gewährleistet schlecht ;
• Es gibt ein „Black-Box“-Problem, schlechte Transparenz, schlechte Rückverfolgbarkeit von Problemen, die im tatsächlichen System auftreten, und es ist schwierig, die Grundursache des Problems zu finden. 4. Wertbasiertes Entscheidungsmodell Alternativen basierend auf den Auswahlkriterien[12].

Um die Qualität jeder Fahraktion zu bewerten, definiert dieser Modelltyp eine Nutzen- oder Wertfunktion, um anhand bestimmter Kriterienattribute quantitativ zu bewerten, inwieweit die Fahrstrategie das Ziel der Fahraufgabe erfüllt Bei autonomen Fahraufgaben können diese Kriteriumsattribute insbesondere Sicherheit, Komfort, Fahreffizienz usw. sein, und Nutzen und Wert können durch ein einzelnes Attribut oder mehrere Attribute bestimmt werden.

Furda und Vlacic von der Griffith University in Australien schlugen eine Entscheidungsmethode mit mehreren Kriterien vor, um die optimale Fahraktion aus dem Aktionsset der Kandidaten auszuwählen [13]; Modell basierend auf POMDP [14], um Situationen zu lösen, in denen eine wahrgenommene Unsicherheit besteht; Wei J und andere von der Carnegie Mellon University schlugen ein Verhaltensentscheidungsmodell basierend auf PCB (Prediction and-Cost-Function Based) [15] vor, das sich darauf konzentriert Wie man eine geeignete Kostenfunktion erstellt, um die Vorhersage der Umgebung zu leiten; um das Entscheidungsproblem in komplexen Umgebungen mit mehreren Agenten zu lösen, werden von Forschern auch viele auf Spieltheorie basierende Modelle verwendet, um darüber nachzudenken interaktives Verhalten zwischen Fahrzeugen [16], [17] Darüber hinaus wird die Deep Reinforcement Learning-Technologie aufgrund ihrer Vorteile bei der Merkmalsextraktion auch häufig zur Generierung optimaler Fahraktionen eingesetzt [18].

04 Bewegungsplanung

Nachdem wir das spezifische Fahrverhalten ermittelt haben, müssen wir das „Verhalten“ in eine spezifischere Fahr-„Trajektorie“ umwandeln, damit wir schließlich eine Reihe spezifischer Steuerungen für die Fahrzeugsignale generieren können damit das Fahrzeug entsprechend dem geplanten Ziel fahren kann. Dieser Prozess wird als Bewegungsplanung bezeichnet. Das Konzept der Bewegungsplanung hat eine lange Forschungsgeschichte auf dem Gebiet der Robotik. Aus mathematischer Sicht können wir es als das folgende Optimierungsproblem betrachten:

Pfadplanung (Pfadplanung)



Abbildung 3. Definition der Pfadplanung

In vielen durch Roboter dargestellten Szenarien können wir die Umgebung als deterministisch betrachten. In diesem Fall bezieht sich die sogenannte Pfadplanung auf das Finden einer Zuordnung σ:[0,1]➞Χ, die bestimmte Einschränkungen in einem bestimmten Zustandsraum Χ erfüllt. Zu diesen Einschränkungen gehören:

• bestimmter Startpunkt Der Anfangszustand und der Bereich, in dem sich der Zielpunkt befindet.
• Kollisionen vermeiden das Optimierungsproblem Es ist als J (σ) definiert und seine spezifische Bedeutung kann als Messstandards wie Pfadlänge und Steuerungskomplexität ausgedrückt werden.
• Bei dem Problem des automatischen Fahrens ändert sich jedoch die Umgebung um das Fahrzeug ständig dynamisch, sodass eine einfache Pfadplanung keine Lösung liefern kann, die während des Fahrprozesses immer gültig ist. Daher müssen wir eine Dimension hinzufügen – Zeit T, entsprechende Planung Das Problem wird oft als Flugbahnplanung bezeichnet.

Trajektorienplanung

Abbildung 4. Definition der Trajektorienplanung

Die Vergrößerung der Zeitdimension bringt große Herausforderungen für das Planungsproblem mit sich. Wenn sich beispielsweise ein Roboter in einer 2D-Umgebung bewegt, die als einzelner Punkt abstrahiert wird, werden die Hindernisse in der Umgebung als Polygone angenähert. Das Pfadplanungsproblem kann in polynomieller Zeit gelöst werden, während sich das Trajektorienplanungsproblem, das die Zeitdimension hinzufügt, als NP-schweres Problem erwiesen hat.

Im tatsächlichen Szenario des autonomen Fahrens, sei es das Fahrzeug selbst oder die Umgebung, bedeutet die Erstellung eines genaueren Modells komplexere Einschränkungen für das Optimierungsproblem und auch eine schwierigere Lösung. Daher basieren die tatsächlich verwendeten Algorithmen auf der Prämisse der Annäherung an die tatsächliche Szene und streben ein optimales Gleichgewicht zwischen Modellgenauigkeit und Lösungseffizienz an.
Im Folgenden werden verschiedene Arten von Bewegungsplanungsalgorithmen vorgestellt, die derzeit im Bereich des autonomen Fahrens üblich sind. In der Praxis ist es oft die Kombination mehrerer Arten von Ideen, die letztendlich bessere Planungsergebnisse erzielen und mehr unterschiedliche Szenarien erfüllen können.

1. Suchbasierter Planungsalgorithmus

Die Lösung von Bewegungsplanungsproblemen durch Suche ist eine der einfachsten Ideen. Die Grundidee besteht darin, den Zustandsraum auf eine bestimmte Weise zu diskretisieren und dann verschiedene heuristische Suchalgorithmen zu verwenden Suche nach realisierbaren Lösungen oder sogar optimalen Lösungen.​​

Bei der Diskretisierung des Zustandsraums sollte darauf geachtet werden, dass das endgültige Gitter den größten Abdeckungsbereich aufweist und sich nicht wiederholt. Wie in Abbildung 5 dargestellt, wird das Gitter auf der linken Seite durch drei Verhaltensweisen erzeugt: geradeaus fahren, um 90° nach links abbiegen und um 90° nach rechts abbiegen. Wenn Sie drei Verhaltensweisen auswählen: geradeaus fahren, um 89° nach links abbiegen und um 89° nach rechts abbiegen; ° ist es nicht möglich, eine flächendeckende Gitterstruktur zu erzeugen.



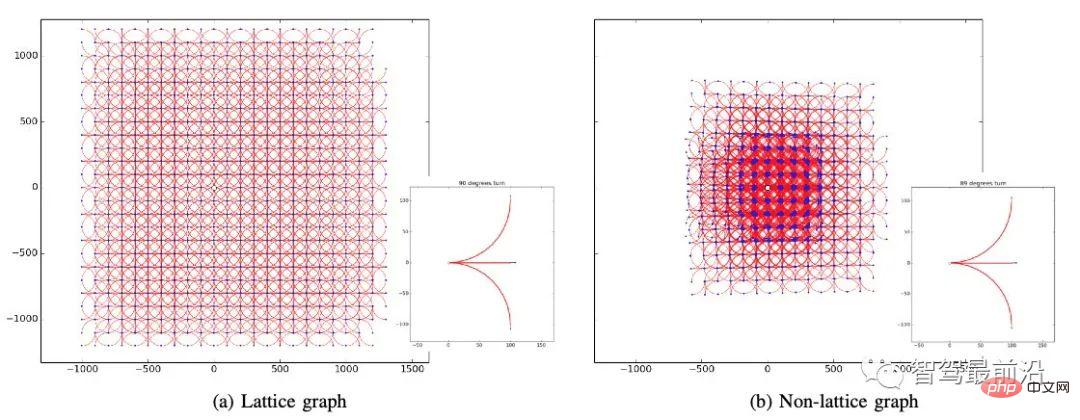
Abbildung 5. Erstellen eines Rasterdiagramms, zitiert aus [2]

Nach der Rasterung des Zustandsraums können wir die oben bereits eingeführten Dijkstra- und A*-Suchalgorithmen verwenden, um die endgültige Planung abzuschließen. In tatsächlichen komplexen Umgebungen gibt es jedoch viele Gitter und die Umgebung ändert sich dynamisch im Laufe der Zeit, was zu zu vielen Suchknoten führt. Daher wurden verschiedene verbesserte Algorithmen entwickelt, um mit verschiedenen spezifischen Szenarien umzugehen:

1) Hybrid Der auf dem A*-Algorithmus basierende A*-Algorithmus berücksichtigt das maximale Lenkproblem des Fahrzeugs und begrenzt beispielsweise die maximale Lenkrichtung des Fahrzeugs auf dem berechneten Weg auf nicht mehr als 5°. Zu den aktuellen Anwendungsszenarien dieses Algorithmus gehören Kehrtwendungen (das von Stanford für die Teilnahme an der DARPA-Herausforderung verwendete Junior-Auto verwendete diesen Algorithmus zur Durchführung einer Kehrtwende), Parken und andere Szenarien, die eine hohe Lenkradkontrolle erfordern.

2) D*- und D*Lite-Algorithmen suchen im Voraus vom Endpunkt zum Startpunkt und verwenden den Dijkstra-Algorithmus, um die kürzeste Pfadlänge k vom Zielpunkt zu jedem Punkt im Straßennetz und die tatsächliche zu speichern Der Längenwert vom Knoten zum Zielpunkt h, im Anfangsfall k==h, und der vorherige Knoten jedes Knotens werden gespeichert, um sicherzustellen, dass der Link verfolgt werden kann.

Nachdem die Berechnung abgeschlossen ist, wird ein zu diesem Zeitpunkt optimaler Pfad ermittelt. Wenn das Auto zu einem bestimmten Knoten fährt und durch den Sensor feststellt, dass der Knoten unpassierbar ist (es gibt Hindernisse), wird der h-Wert einiger relevanter Punkte in den gespeicherten Straßennetzinformationen geändert (erhöht) und ein Nachbarpunkt ausgewählt erfüllt immer noch das Problem h==k, das heißt, der Punkt auf dem optimalen Pfad ist immer noch der nächste Punkt.

Dann gehen Sie bis zum Ende. Diese Art von Algorithmus eignet sich für die Navigation und Pfadplanung in unbekannten Umgebungen und wird häufig in verschiedenen aktuellen mobilen Robotern und autonomen Fahrzeugen eingesetzt, beispielsweise in den Marsrovern „Opportunity“ und „Spirit“.

2. Der auf Stichproben basierende Planungsalgorithmus

nähert sich dem ursprünglichen Problem durch Abtasten des kontinuierlichen Zustandsraums an. Bei Bewegungsplanungsproblemen gehören zu den grundlegenden auf Stichproben basierenden Algorithmen die Algorithmen Probabilistic Roadmap (PRM) und Rapid Search Random Tree (RRT).



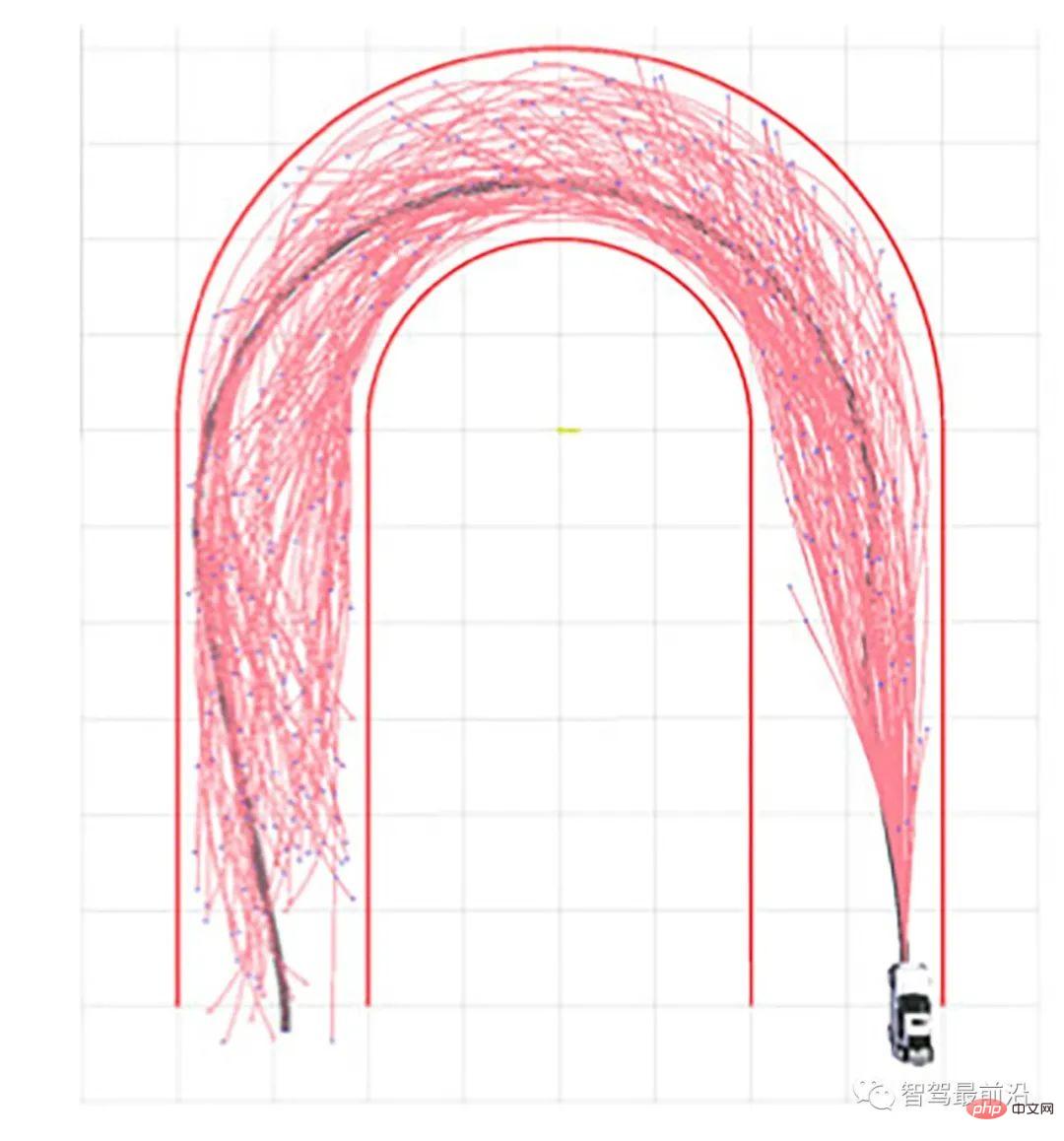
Abbildung 6. U-förmige Biegetrajektorienplanung mit RRT-Algorithmus, zitiert aus [19]

1) Basisalgorithmus: Probabilistic Roadmap (PRM)


• Vorverarbeitungsphase: Zustandsraum n Punkte sind gleichmäßig und zufällig im sicheren Bereich innerhalb des Netzwerks abgetastet, und jeder Abtastpunkt wird mit benachbarten Abtastpunkten innerhalb einer bestimmten Entfernung verbunden, und Trajektorien, die mit Hindernissen kollidieren, werden verworfen, und schließlich wird ein verbundener Graph erhalten.
• Abfragephase: Verbinden Sie ein bestimmtes Paar aus Anfangs- und Zielzuständen mit dem bereits erstellten Diagramm und verwenden Sie dann den Suchalgorithmus, um eine Trajektorie zu finden, die den Anforderungen entspricht.

Es ist leicht zu erkennen, dass ein einmal erstelltes PRM zur Lösung von Bewegungsplanungsproblemen in verschiedenen Anfangs- und Zielzuständen verwendet werden kann, diese Funktion jedoch für die Bewegungsplanung beim autonomen Fahren nicht erforderlich ist. Darüber hinaus erfordert PRM präzise Verbindungen zwischen Zuständen, was bei Bewegungsplanungsproblemen mit komplexen Differentialbeschränkungen sehr schwierig ist.

2) Grundalgorithmus: Rapid Search Random Tree (RRT)

• Initialisierung des Baums: Initialisieren Sie den Knotensatz und den Kantensatz des Baums. Der Knotensatz enthält nur den Anfangszustand und der Kantensatz ist leer .
• Baumwachstum: Stichproben Sie den Zustandsraum zufällig ab. Wenn der Stichprobenpunkt in den sicheren Bereich des Zustandsraums fällt, wählen Sie den Knoten aus, der dem Stichprobenpunkt im aktuellen Baum am nächsten liegt, und erweitern (oder verbinden) Sie ihn mit dem Stichprobenpunkt . Wenn die generierte Trajektorie nicht mit Hindernissen kollidiert, wird die Trajektorie zum Kantensatz des Baums hinzugefügt und der Endpunkt der Trajektorie wird zum Knotensatz des Baums hinzugefügt.

RRT ist eine inkrementelle Stichprobensuchmethode, für die keine Einstellung von Auflösungsparametern erforderlich ist. Im Extremfall deckt der Suchbaum den gesamten Raum dicht ab. Zu diesem Zeitpunkt besteht der Suchbaum aus vielen kürzeren Kurven oder Pfaden, um den Zweck zu erreichen, den gesamten Raum auszufüllen.

3) Verschiedene verbesserte Algorithmen

Aus der Beschreibung des obigen Grundalgorithmus können wir verstehen, dass das Abtasten des Zustandsraums eine praktikable Lösung sicherstellen kann, die den Startpunkt und den Endpunkt verbindet, aber da der Abtastvorgang durchgeführt wird Im gesamten Raum ist die Probenahme sehr gering, sodass in komplexen Szenarien keine Echtzeitlösung erzielt werden kann. Darüber hinaus kann das endgültige Planungsergebnis nicht garantieren, dass die erhaltene realisierbare Lösung die optimale ist. Als Reaktion auf diese Nachteile wurden verschiedene verbesserte Algorithmen vorgeschlagen und auf autonome Fahrprobleme angewendet:

• Effizienzverbesserung – ungleichmäßige Abtastung

- RRT-Connect: Konstruieren Sie gleichzeitig zwei Bäume, beginnend mit dem Anfangszustand und dem Ziel Zustand: Wenn zwei Bäume zusammenwachsen, wird eine praktikable Lösung gefunden.

- Heuristik (hRRT): Verwenden Sie eine heuristische Funktion, um die Wahrscheinlichkeit zu erhöhen, dass Knoten mit niedrigen Erweiterungskosten abgetastet werden.

- Kombiniert mit dem Fahrermodell: In Kombination mit dem visuellen Aufmerksamkeitsmodell des Fahrers für voreingenommene Stichproben werden visuelle Merkmalsinformationen zur Steuerung der Bewegungsplanung verwendet, sodass die geplante Flugbahn besser mit dem menschlichen Fahrverhalten übereinstimmt.

- Erstellen Sie eine neue Metrik RG-RRT (Reachability Guided RT): Die herkömmliche euklidische Distanzmetrik kann den Abstand zwischen Konfigurationen oder Zuständen nicht wirklich widerspiegeln. RG-RRT berechnet den Erreichbarkeitssatz von Knoten im Baum Ist der Abstand zu einem Knoten größer als der Abstand vom Abtastpunkt zum Knoten, kann der Knoten für die Erweiterung ausgewählt werden.

- Hindernisstrafe hinzufügen (RC-RRT, EG-RRT, ADD-RRT usw.): Reduzieren Sie die Wahrscheinlichkeit, dass Knoten in der Nähe von Hindernissen erweitert werden.

• Echtzeit-Verbesserung

– RRT erstellt zu jedem Zeitpunkt schnell eine RRT, erhält eine praktikable Lösung und zeichnet deren Kosten auf. Danach führt der Algorithmus die Stichprobenentnahme fort, fügt jedoch nur Knoten in den Baum ein, die für die Reduzierung von Vorteil sind Kosten der realisierbaren Lösung, so dass nach und nach bessere realisierbare Lösungen erhalten werden.

- Bei der Neuplanung wird die gesamte Planungsaufgabe in mehrere zeitgleiche Unteraufgabensequenzen zerlegt und die nächste Aufgabe geplant, während die aktuelle Aufgabe ausgeführt wird.

• Optimalitätsverbesserung

- PRM*, RRG, RRT*: Gemäß der Theorie des zufälligen geometrischen Graphen (zufälliges Abtasten von m Punkten im Zustandsraum und Verbinden der Punkte mit einem Abstand kleiner als r(n)) entsteht Random geometrische Diagramme) wurden gegenüber den Standard-PRM- und RRT-Algorithmen verbessert und es wurden die PRM*-, RRG- und RRT*-Algorithmen mit asymptotischen optimalen Eigenschaften erhalten

3 Direkte Optimierungsmethode

In den meisten Fällen werden Änderungen nicht berücksichtigt In der Höhe ist das Flugbahnplanungsproblem des autonomen Fahrens ein dreidimensionales eingeschränktes Optimierungsproblem (2D-Raum + Zeit T). Daher können wir eine Entkopplungsstrategie verwenden, um das ursprüngliche Problem in mehrere niedrigdimensionale Probleme zu zerlegen und dadurch das Problem erheblich zu reduzieren Problem der Lösung des Problems.

1) Frenet-Koordinatensystem




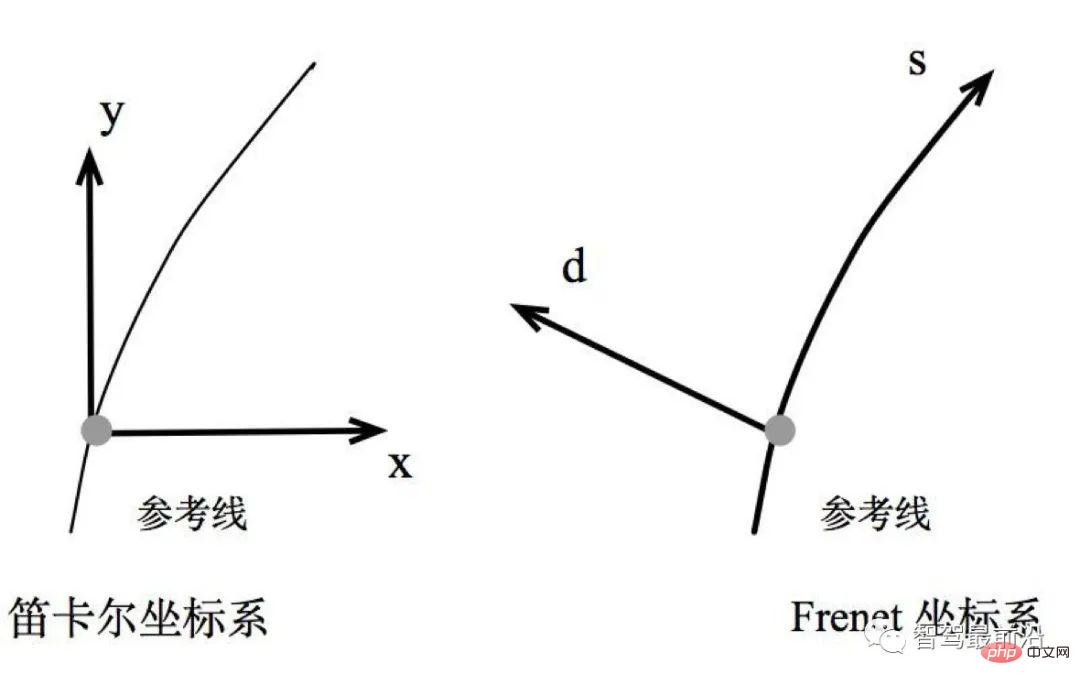
Abbildung 7. Frenet-Koordinatensystem

Da die Straßen in der realen Welt gekrümmt sind, wird Frenet normalerweise verwendet, um den Parameterausdruck bei der Lösung von Optimierungsproblemen zu vereinfachen Koordinatensystem für autonomes Fahren.

Im Frenet-Koordinatensystem verwenden wir die Mittellinie der Straße als Referenzlinie und verwenden den Tangentenvektor t und den Normalenvektor n der Referenzlinie, um ein Koordinatensystem zu erstellen, wie im Bild rechts gezeigt. Dabei handelt es sich um das Fahrzeug selbst als Ursprung und die Koordinatenachse, die senkrecht zueinander steht. Es wird in s-Richtung (d. h. die Richtung entlang der Referenzlinie, üblicherweise Längsrichtung, Longitudinal genannt) und d-Richtung (bzw. L-Richtung) unterteilt , die aktuelle Normalrichtung der Referenzlinie, genannt transversal, lateral). Im Vergleich zum kartesischen Koordinatensystem (linkes Bild) vereinfacht das Frenet-Koordinatensystem das Problem erheblich.

Da wir beim Fahren auf der Straße immer leicht die Referenzlinie der Straße (d. h. die Mittellinie der Straße) finden können, kann die Position basierend auf der Referenzlinie einfach durch den Längsabstand S (d. h. , entlang der Straßenrichtung) Abstand) und der seitliche Abstand L (d. h. der Abstand von der Referenzlinie entfernt).

2) Weg-Geschwindigkeits-Entkopplungsmethode


Im Frenet-Koordinatensystem optimiert die Weg-Geschwindigkeits-Entkopplungsmethode hauptsächlich statische Hindernisse und generiert einen statischen Referenzpfad durch dynamische Planung. SL-Dimension) und berücksichtigen Sie dann basierend auf dem generierten Pfad die Geschwindigkeitsplanung (ST-Dimension). Dieser Prozess kann kontinuierlich iteriert werden und ermöglicht so Echtzeitaktualisierungen der Flugbahn. Der EM-Planer, der in Baidus Open-Source-Plattform für autonomes Fahren Apollo verwendet wird, basiert auf einer ähnlichen Lösung. Diese Lösung ist sehr flexibel und kann universell auf viele Szenarien angewendet werden.

Darüber hinaus können Sie auch verschiedene Entkopplungsmethoden wählen, wie z. B. die getrennte Planung der Längstrajektorie (ST-Dimension) und Quertrajektorie (LT-Dimension). Es sollte jedoch darauf hingewiesen werden, dass die durch die Entkopplungsmethode erhaltene Lösung möglicherweise nicht optimal ist, dieser Algorithmus nicht vollständig ist und in einigen komplexen Umgebungen möglicherweise keine praktikable Lösung gefunden wird.

4. Parametrische Kurvenkonstruktionsmethode



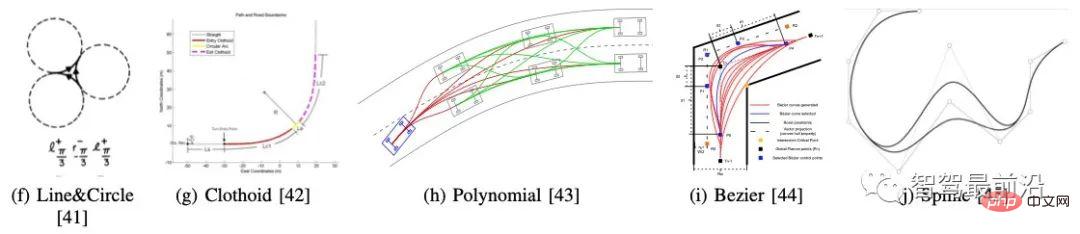
Abbildung 8. Gängige parametrische Kurvenkonstruktionsmethode, zitiert aus [19]

Der Ausgangspunkt der parametrischen Kurvenkonstruktionsmethode sind die Einschränkungen des Fahrzeugs selbst, einschließlich der Kinematik Da es Einschränkungen hinsichtlich der Dynamik gibt, muss der allgemein geplante Pfad eine kontinuierliche Krümmung aufweisen. Diese Art von Methode berücksichtigt Hindernisse basierend auf dem Startpunkt und dem Zielpunkt und sorgt für einen glatten Pfad durch die Konstruktion einer Kurvenfamilie, die den Fahrzeugbeschränkungen entspricht.

Wie in Abbildung 8 gezeigt, gehören zu den gängigen Kurven die Dubins-Kurve (bestehend aus geraden Linien und Bögen, die kürzeste Kurvenfamilie eines einfachen Dubin-Modells für Fahrzeugmodelle im zweidimensionalen Raum), die Klothoidenkurve, die Polynomkurve und die Bezier-Kurve , Splines usw. Es ist schwierig, die parametrische Kurvenkonstruktionsmethode einfach anzuwenden, um tatsächlich komplexe Szenarien zu erfüllen. Daher kombinieren immer mehr autonome Fahrsysteme sie mit anderen Methoden, um die geplanten und generierten Trajektorien zu glätten, um den Einschränkungen der Fahrzeugkinematik und -dynamik gerecht zu werden.

5. Künstliche Potenzialfeldmethode

Die Methode des künstlichen Potenzialfelds ist vom elektromagnetischen Feld in der Physik inspiriert. Es wird davon ausgegangen, dass Hindernisse und Zielpositionen Abstoßung bzw. Schwerkraft erzeugen, sodass der Weg entlang des schnellsten Gradientenabfalls des Potenzialfelds geplant werden kann. Ein zentrales Problem bei dieser Art von Methode ist die Auswahl einer geeigneten Potenzialfeldfunktion. Beispielsweise verwendet Stephen Waydo Strömungsfunktionen für eine reibungslose Pfadplanung [20], und Robert Daily schlägt eine Methode zur Planung eines harmonischen Potenzialfeldpfads für Hochgeschwindigkeitsfahrzeuge vor [21]. In einfachen Szenarien weist die Methode des künstlichen Potenzialfelds eine hohe Lösungseffizienz auf, ihr größtes Problem besteht jedoch darin, dass sie möglicherweise in ein lokales Minimum fällt. In diesem Fall ist der erhaltene Pfad nicht optimal und der Pfad kann möglicherweise nicht einmal gefunden werden.

05 Algorithmuskomplexität (Komplexität)

Bei Planungsproblemen muss bei der Bewertung eines Algorithmus neben der Berücksichtigung seiner zeitlichen und räumlichen Komplexität auch berücksichtigt werden, ob er vollständig und optimal ist. Als Nächstes wird geprüft, ob er probabilistisch ist Vollständigkeit und asymptotische Optimalität. Nur auf der Grundlage des Verständnisses dieser Eigenschaften können wir verschiedene Algorithmen für verschiedene tatsächliche Szenarien entwerfen und anwenden, um so das beste Gleichgewicht zwischen Modellkomplexität und optimaler Effizienz zu erreichen.

1) Vollständigkeit: Wenn es eine Pfadlösung zwischen dem Startpunkt und dem Zielpunkt gibt, muss die Lösung erhalten werden. Wenn die Lösung nicht erhalten werden kann, bedeutet dies, dass es keine Lösung gibt.

2) Wahrscheinlichkeitsvollständigkeit (Wahrscheinlich) Vollständigkeit): Wenn es eine Pfadlösung zwischen dem Startpunkt und dem Zielpunkt gibt, wird, solange die Planungs- oder Suchzeit lang genug ist, sicher eine Pfadlösung gefunden

3) Optimalität: Die Der geplante Pfad ist innerhalb eines bestimmten Bewertungsindex optimal (der Bewertungsindex ist im Allgemeinen die Länge des Pfads).

4) Asymptotische Optimalität: Der nach einer begrenzten Anzahl von Planungsiterationen erhaltene Pfad ist ein suboptimaler Pfad, der nahe bei liegt optimal, und nach jeder Iteration nähert es sich dem optimalen Pfad, was ein allmählicher Konvergenzprozess ist. Tabelle 1 Vergleich gängiger Algorithmen: 06 Zukünftige Entwicklungstrends: Abbildung 9. Zeitleiste für die Entwicklung autonomer Fahrsysteme und Prozess Wichtiger Bewegungsplanungsalgorithmus, zitiert aus [19]

Das menschliche Interesse am autonomen Fahren lässt sich bis ins Jahr 1925 zurückverfolgen. In den letzten Jahren begann der Forschungsboom im autonomen Fahren mit der US-amerikanischen Defense Advanced Research Projects Agency (DARPA). drei Herausforderungen beim autonomen Fahren von 2004 bis 2007 [22], wie in Abbildung 9 dargestellt. Anschließend wurde die Wirksamkeit der verschiedenen oben genannten Methoden zur Entscheidungsfindung tatsächlich überprüft. Gleichzeitig entstehen weiterhin Lösungen, die Bewegungsplanungsmethoden mit Steuerungstheorie, Zustandsparameterschätzung, maschinellem Lernen und anderen Mehrfeldmethoden kombinieren und sich zu einem zukünftigen Entwicklungstrend entwickeln:

1) Kombination mit Fahrzeugdynamik: Bewertung dynamischer Parameter Kombination Indikatoren mit optimaler Planung, die Planung aus der Perspektive der optimalen Steuerung ist eine Methode, die in den letzten Jahren häufiger verwendet wurde. Dabei können Fahrzeugdynamikfaktoren vollständig berücksichtigt werden, und die geplante Flugbahn ist vernünftiger. Verwenden Sie beispielsweise die modellprädiktive Steuerungstheorie (Model Predictive Control). Der Nachteil besteht darin, dass es umso schwieriger ist, seine Flugbahn zu optimieren und eine Online-Echtzeitberechnung durchzuführen, je mehr Einschränkungen das Fahrzeug hat.
2) Kombiniert mit der Zustandsparameterschätzung: Die Zustandsparameterschätzung kann Fahrzeugparameter genauer ermitteln, sodass der Zustandsschätzer zum Planungsmodul hinzugefügt werden kann, um die Trajektorienqualität zu verbessern, indem der Fahrzeugzustand online geschätzt und an den Planer zurückgegeben wird. Beispielsweise führen unterschiedliche Bodentypen zu Änderungen der Schlupfeigenschaften des Fahrzeugs und wirken sich dadurch auf den Fahrzeugstatus aus. Durch die Kombination geschätzter Parameter kann die Flugbahn in Echtzeit neu geplant werden, und eine geschlossene Planung kann die Flugbahnsicherheit verbessern.
3) Kombination mit maschinellem Lernen: Mit der rasanten Entwicklung der künstlichen Intelligenz, repräsentiert durch neuronale Netze, haben viele traditionelle Planungsprobleme auch neue Lösungen gebracht. Zu den Entwicklungstrends im Bereich des autonomen Fahrens gehören:
• End-to-End-Modell: Verwenden Sie ein tiefes neuronales Netzwerk, um das Steuersignal des Fahrzeugs basierend auf dem Fahrzeugstatus und externen Umgebungsinformationen direkt abzuleiten. Obwohl das aktuelle End-to-End-Modell nicht wie eine „Black Box“ interpretiert werden kann, wird davon ausgegangen, dass diese Methode aufgrund ihrer herausragenden Vorteile in Bezug auf Einfachheit und Effizienz ein großes Entwicklungspotenzial aufweist, da der Mensch sein Verständnis tiefer neuronaler Netze immer weiter vertieft.
• Integration von Entscheidungs- und Bewegungsplanungsmodulen
• Autonome Fahrzeuge treffen optimale Entscheidungen in komplexen Umgebungen. Dieses Problem steht daher, wie oben erwähnt, mit der schnellen Entwicklung der Deep-Reinforcement-Learning-Technologie. Immer mehr Forschungsteams haben damit begonnen, es auf die Entscheidungsplanung für autonomes Fahren anzuwenden und Module zur Verhaltensentscheidung und Bewegungsplanung zu integrieren, um Fahrtrajektorien direkt zu lernen. Um das Problem zu lösen, dass die Umweltbelohnungsfunktion nicht einfach zu erhalten ist, wurde auch vorgeschlagen, zunächst inverses Verstärkungslernen (IRL) zu verwenden, um auf der Grundlage menschlicher Expertendemonstrationen zu lernen, und dann Verstärkungslernen zu verwenden, um die optimale Richtlinie zu lernen.

Das obige ist der detaillierte Inhalt vonDetaillierte Erläuterung der Entscheidungsplanungstechnologie für autonomes Fahren. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!