Heim >Technologie-Peripheriegeräte >KI >Eine kurze Analyse des maschinellen Lernens und der Differentialgleichungen
Eine kurze Analyse des maschinellen Lernens und der Differentialgleichungen
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2023-04-04 12:10:071530Durchsuche
Obwohl es maschinelles Lernen schon seit den 1950er Jahren gibt, als Computer immer leistungsfähiger wurden und die Datenmenge explodierte, gibt es umfangreiche Untersuchungen darüber, wie Menschen künstliche Intelligenz nutzen können, um sich einen Wettbewerbsvorteil zu verschaffen, Erkenntnisse zu verbessern und ihre Gewinne zu steigern. Für unterschiedliche Anwendungsszenarien bieten maschinelles Lernen und Differentialgleichungen ein breites Spektrum an Szenarien.
Jeder hat bereits maschinelles Lernen genutzt, insbesondere Deep Learning auf Basis neuronaler Netze. ChatGPT ist sehr beliebt. Müssen Sie Differentialgleichungen noch im Detail verstehen? Egal wie die Antwort lautet, es wird einen Vergleich zwischen beiden erfordern. Was ist also der Unterschied zwischen maschinellem Lernen und Differentialgleichungen?
Beginnen Sie mit den Differentialgleichungen des Liebesmodells
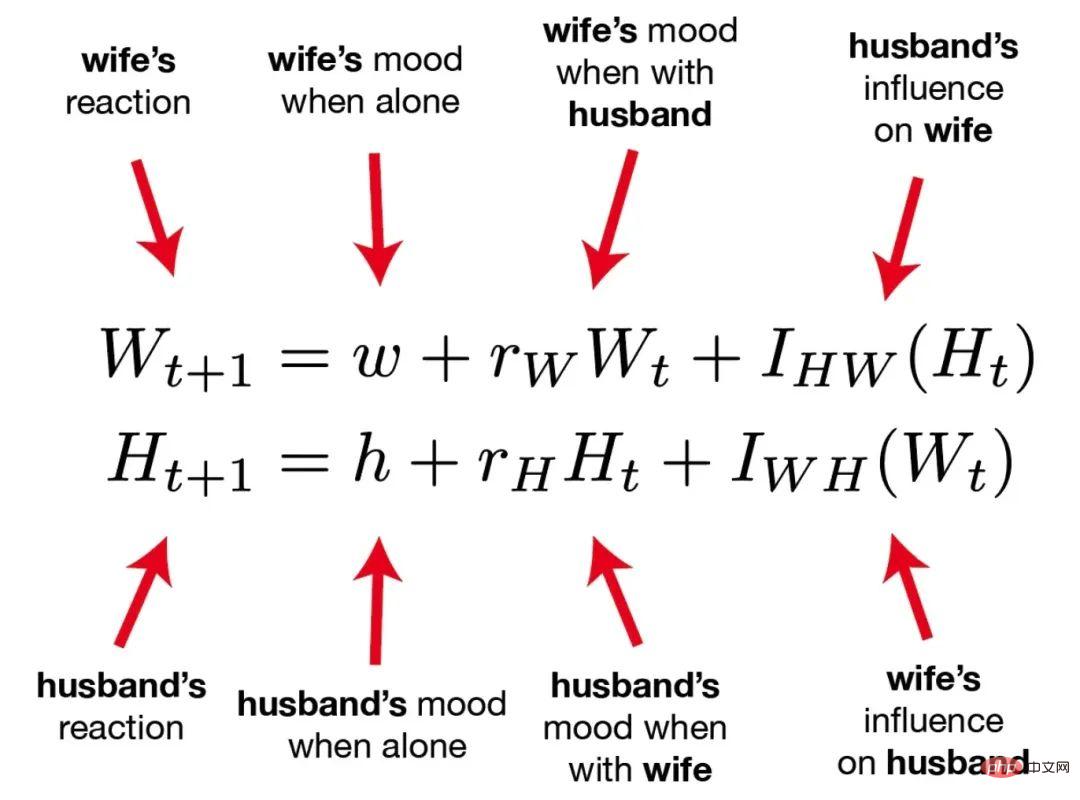
Diese beiden Gleichungen sagen die Langlebigkeit der Liebesbeziehung eines Paares voraus. Basierend auf der Pionierarbeit des Psychologen John Gottman sagt dieses Modell voraus, dass anhaltende positive Emotionen der Schlüssel sind zur Ehe. Ein starker Erfolgsfaktor. Weitere Interpretationen des Modells finden Sie im Buch „Glückliche Ehe“. Der Autor nennt außerdem 7 Regeln für die Aufrechterhaltung einer glücklichen Ehe:
- Verbessern Sie Ihre Liebeskarte
- Kultivieren Sie Ihre Liebe und Ihr Lob für Ihren Ehepartner
- Bleiben Sie näher beieinander statt weit weg
- Lassen Sie Ihren Ehepartner Ihre Entscheidung beeinflussen
- Beginnen Sie mit Sanftmut und enden Sie mit Kompromissen
- Lernen Sie, mit Problemen im Einklang zu leben
- Schaffen Sie eine gemeinsame Bedeutung
Jeder hat die Epidemie schon einmal erlebt Drei Jahre, und wir wissen, was gut und was schlecht ist. Wie lässt sich also die Beziehung zwischen Patienten und infektiösen Personen mithilfe von Differentialgleichungen beschreiben?

Das SIR-Modell geht davon aus, dass das Virus durch direkten Kontakt zwischen infizierten und nicht infizierten Menschen verbreitet wird, wobei sich erkrankte Menschen automatisch mit einer festgelegten Rate erholen.
Diese Differentialgleichungen enthalten alle die Ableitungen (dh die Änderungsrate) einiger unbekannter Funktionen, wie z. B. S (t), I (t) und R (t) im SIR-Modell, werden Lösungen genannt zur Differentialgleichung. Basierend auf der Mechanik dieser Gleichungen können wir ableiten, wie das Modell konzipiert ist, und die Daten werden später zur Überprüfung unserer Hypothesen verwendet.
Klassifizierung mathematischer Modelle
Mathematische Modelle wie Differentialgleichungen machen im Voraus Annahmen über den grundlegenden Mechanismus des Systems. Tatsächlich begann das gesamte Gebiet der mathematischen Modellierung im 17. Jahrhundert der fundamentalen Dynamik dahinter. Seitdem haben mathematisch basierte mechanistische Modelle wichtige Einblicke in viele Phänomene ermöglicht, von der Biologie und dem Ingenieurwesen bis hin zu den Wirtschafts- und Sozialwissenschaften. Solche Mechanismusmodelle können in gleichungsbasierte Modelle, beispielsweise Differentialgleichungen, oder agentenbasierte Modelle unterteilt werden.
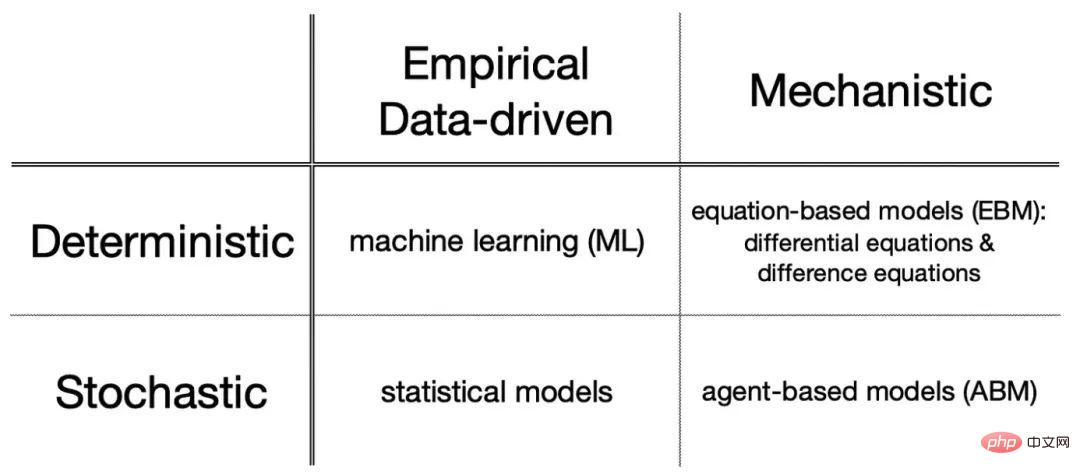
Bei der erfahrungsbasierten oder datengesteuerten Modellierung, wie zum Beispiel maschinellem Lernen, geht es darum, die Struktur eines Systems anhand umfangreicher Daten zu verstehen. Maschinelles Lernen ist besonders nützlich für komplexe Systeme, bei denen wir nicht wirklich wissen, wie wir das Signal vom Rauschen trennen können, und bei denen das einfache Training eines cleveren Algorithmus zur Lösung des Problems beitragen kann.
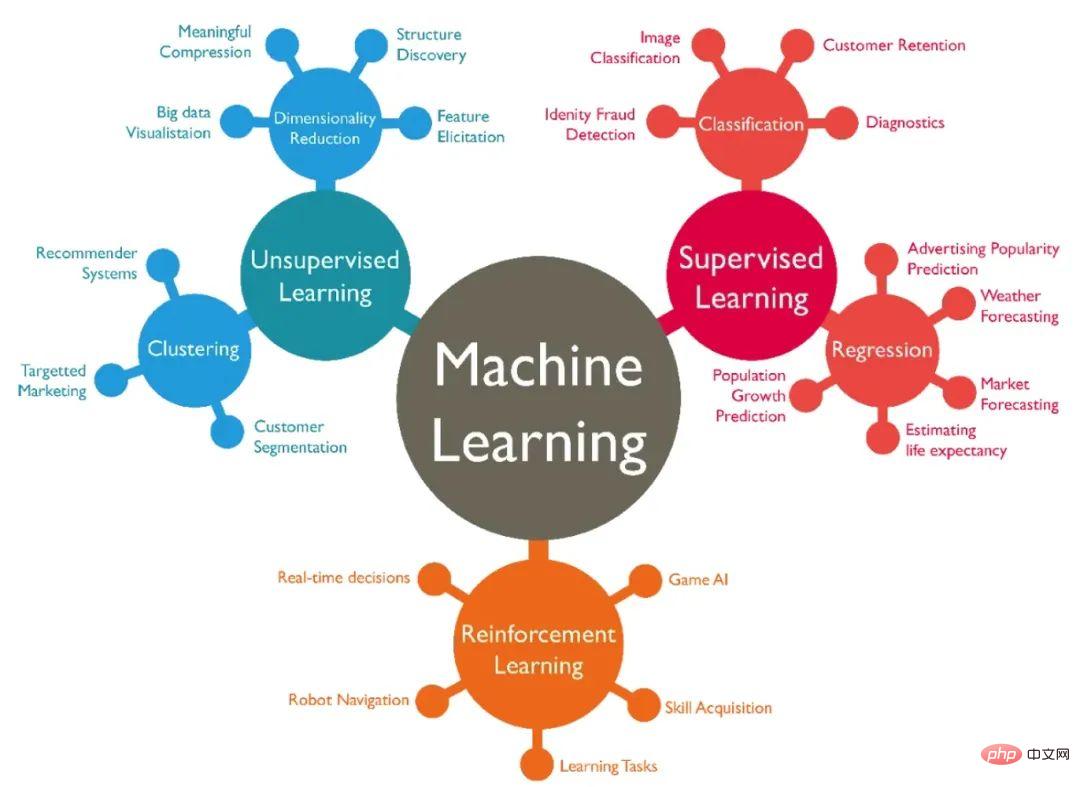
Maschinelle Lernaufgaben können grob in die folgenden Kategorien unterteilt werden:
- überwachtes Lernen (z. B. Regression und Klassifizierung);
- unüberwachtes Lernen (z. B. Clustering und Dimensionsreduktion);
- Verstärkendes Lernen
Fortschrittliche Systeme für maschinelles Lernen und künstliche Intelligenz sind mittlerweile überall in unserem täglichen Leben zu finden, von intelligenten lautsprecherbasierten Gesprächsassistenten (wie Xiaodu) über verschiedene Empfehlungsmaschinen bis hin zu Gesichtserkennungstechnologie und sogar Teslas selbstfahrendem Auto. All dies wird durch mathematische und statistische Modelle angetrieben, die in Bergen von Code eingebettet sind.
Darüber hinaus können diese Modelle als „deterministisch“ (Vorhersagen sind fest) oder „stochastisch“ (Vorhersagen beinhalten Zufälligkeiten) klassifiziert werden.
Deterministische Modelle ignorieren Zufallsvariablen und sagen immer das gleiche Ergebnis unter den gleichen Startbedingungen voraus. Im Allgemeinen sind maschinelles Lernen und gleichungsbasierte Modelle deterministisch und die Ausgabe ist immer vorhersehbar. Mit anderen Worten: Die Ausgabe wird vollständig durch die Eingabe bestimmt.
Stochastische Modelle berücksichtigen zufällige Veränderungen in der Bevölkerung, indem sie Wahrscheinlichkeiten in das Modell einführen. Eine Möglichkeit, diese Änderungen zu erfassen, besteht darin, jede Entität zu einem separaten Agenten im Modell zu machen und zulässige Verhaltensweisen und Mechanismen für diese Agenten zu definieren, die bestimmte Wahrscheinlichkeiten haben. Dabei handelt es sich um agentenbasierte Modelle.
Allerdings ist die Modellierung einzelner Akteure mit Kosten verbunden, und agentenbasierte Modelle sind realistischer. Aufgrund des hohen Rechenaufwands und der Interpretierbarkeit des Modells inspirierte dies ein Schlüsselkonzept der mathematischen Modellierung: die Modellkomplexität.
Modellkomplexität
Das Dilemma der Modellkomplexität ist eine Realität, mit der alle Modellierer konfrontiert sind. Unser Ziel ist es, Modelle zu erstellen und zu optimieren, die weder zu einfach noch zu komplex sind. Einfache Modelle sind leicht zu analysieren, haben jedoch häufig keine Vorhersagekraft. Komplexe Modelle mögen surreal sein, aber es ist möglich, zu versuchen, die Wahrheit hinter komplexen Problemen zu verstehen.
Wir müssen einen Kompromiss zwischen Einfachheit und einfacher Analyse eingehen. Komplexe Modelle für maschinelles Lernen streben danach, das Signal (d. h. die wahre Struktur des Systems) zu lernen und gleichzeitig das Rauschen (d. h. Interferenzen) zu unterdrücken. Dies führt dazu, dass das Modell bei neuen Daten eine schlechte Leistung erbringt. Mit anderen Worten: Modelle des maschinellen Lernens sind weniger verallgemeinerbar.
Der heikle Akt, die Modellkomplexität auszubalancieren, ist eine „Kunst“, bei der versucht wird, einen Sweet Spot zu finden, der weder zu einfach noch zu komplex ist. Dieses ideale Modell beseitigt den Lärm, erfasst die zugrunde liegende Dynamik des Geschehens und ist einigermaßen erklärbar.
Es ist wichtig zu beachten, dass dies bedeutet, dass ein gutes mathematisches Modell nicht immer korrekt ist. Aber es spielt keine Rolle. Das Ziel besteht in der Generalisierbarkeit, d. h. einem Publikum erklären zu können, warum das Modell tut, was es tut, unabhängig davon, ob es sich um Akademiker, Ingenieure oder Wirtschaftsführer handelt.
Differentialgleichungen vs. maschinelles Lernen Bei der Mechanismusmodellierung beobachten und untersuchen wir ein Phänomen sorgfältig, bevor wir Annahmen über den zugrunde liegenden Mechanismus des Systems treffen und das Modell dann anhand von Daten validieren. Sind unsere Annahmen richtig? Wenn ja, ist es durchaus möglich, jedem zu erklären, welches Modell sich auf diese Weise verhält, da es sich um einen handverlesenen Mechanismus handelt. Wenn die Annahme falsch ist, ist das in Ordnung, Sie haben nur etwas Zeit verschwendet, keine große Sache. Modellieren ist schließlich Versuch und Irrtum. Spielen Sie mit diesen Annahmen oder fangen Sie sogar ganz von vorne an. Mechanismusmodelle, meist Gleichungen in Form von Differentialgleichungen oder auch agentenbasierte Modelle. Bei der datengesteuerten Modellierung lassen wir zunächst die Daten wirken und erstellen für uns eine Panoramaansicht des Systems. Wir müssen lediglich die Datenqualität dieser Maschine erfüllen und hoffentlich über genügend Daten verfügen. Das ist maschinelles Lernen. Wenn ein Phänomen für normale Menschen schwer zu verstehen ist, kann eine Maschine so eingestellt werden, dass sie das Rauschen durchsiebt und das für uns schwer fassbare Signal lernt. Zu den Standardaufgaben des maschinellen Lernens gehören Regression und Klassifizierung, die anhand einer Reihe von Metriken bewertet werden. Auch neuronale Netze und Reinforcement Learning erfreuen sich großer Beliebtheit und ermöglichen es ihnen, Modelle zu erstellen und überraschend komplexe Signale zu lernen. Obwohl es maschinelles Lernen schon seit den 1950er Jahren gibt, gab es mit der zunehmenden Leistungsfähigkeit von Computern und der explosionsartigen Verbreitung von Daten eine breite Ausweitung der Möglichkeiten, wie Menschen künstliche Intelligenz nutzen können, um sich einen Wettbewerbsvorteil zu verschaffen, Erkenntnisse zu verbessern und ihre Gewinne zu steigern . Für unterschiedliche Anwendungsszenarien bieten maschinelles Lernen und Differentialgleichungen ein breites Spektrum an Szenarien.Alle Modelle sind falsch, aber einige sind nützlich. ——George Box, 1976 Im maschinellen Lernen und in der Statistik wird die Modellkomplexität als Bias-Varianz-Kompromiss bezeichnet. Modelle mit hohem Bias sind zu einfach, was zu einer Unteranpassung führt, während Modelle mit hoher Varianz Rauschen anstelle von Signalen speichern, was zu einer Überanpassung führt. Datenwissenschaftler streben danach, dieses empfindliche Gleichgewicht durch sorgfältige Auswahl der Trainingsalgorithmen und Abstimmung der zugehörigen Hyperparameter zu erreichen.
Das obige ist der detaillierte Inhalt vonEine kurze Analyse des maschinellen Lernens und der Differentialgleichungen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Technologietrends, die Sie im Jahr 2023 im Auge behalten sollten
- Wie künstliche Intelligenz Rechenzentrumsteams neue Alltagsaufgaben beschert
- Können künstliche Intelligenz oder Automatisierung das Problem der geringen Energieeffizienz in Gebäuden lösen?
- OpenAI-Mitbegründer im Interview mit Huang Renxun: Die Argumentationsfähigkeiten von GPT-4 haben noch nicht die Erwartungen erfüllt
- Dank der OpenAI-Technologie übertrifft Bing von Microsoft Google im Suchverkehr

