Heim >Web-Frontend >js-Tutorial >Detaillierte Einführung in JavaScript-Binärbäume und verschiedene Traversalalgorithmen
Detaillierte Einführung in JavaScript-Binärbäume und verschiedene Traversalalgorithmen
- WBOYnach vorne
- 2022-07-27 17:34:362353Durchsuche
Dieser Artikel vermittelt Ihnen relevantes Wissen über Javascript. Er stellt hauptsächlich die Details von JavaScript-Binärbäumen und verschiedenen Traversal-Algorithmen vor, die einen gewissen Referenzwert haben . Ich hoffe, es hilft allen.

[Verwandte Empfehlungen: Javascript-Video-Tutorial, Web-Frontend]
Was ist ein Binärbaum?
Ein Binärbaum ist ein Baum, in dem jeder Knoten höchstens zwei untergeordnete Knoten haben kann , wie in der folgenden Abbildung gezeigt:
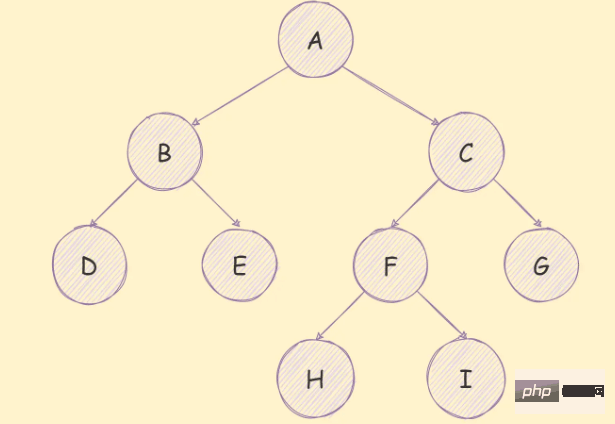
Ein Binärbaum hat die folgenden Eigenschaften:
- Die
i-te Schicht hat höchstens nur2^(i- 1)Knoten;i层的节点最有只有2^(i-1)个; - 如果这颗二叉树的深度为
k,那二叉树最多有2^k-1个节点; - 在一个非空的二叉树中,若使用
n0表示叶子节点的个数,n2是度为2的非叶子节点的个数,那么两者满足关系n0 = n2 + 1。
满二叉树
如果在一个二叉树中,除了叶子节点,其余的节点的每个度都是2,则说明该二叉树是一个满二叉树,
如下图所示:
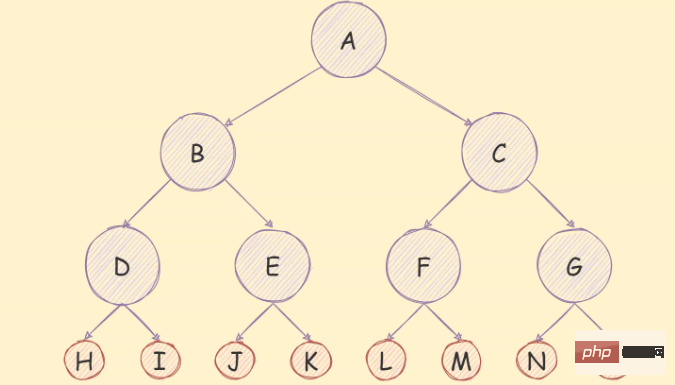
满二叉树除了满足普通二叉树特质,还具有如下几个特质:
- 满二叉树的的第
n层具有2^(n-1)个节点; - 深度为
k的满二叉树一定存在2^k-1个节点,叶子节点的个数为2^(k-1); - 具有
n个节点的满二叉树的深度为log_2^(n+1)。
完全二叉树
如果一个二叉树去掉最后一次层是满二叉树,且最后一次的节点是依次从左到右分布的,则这个二叉树是一个完全二叉树,
如下图所示:
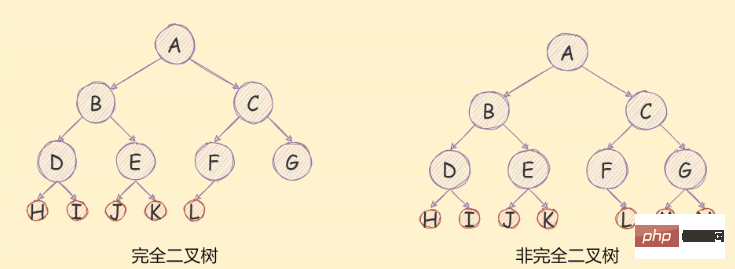
二叉树的存储
存储二叉树的常见方式分为两种,一种是使用数组存储,另一种使用链表存储。
数组存储
使用数组存储二叉树,如果遇到完全二叉树,存储顺序从上到下,从左到右,如下图所示:
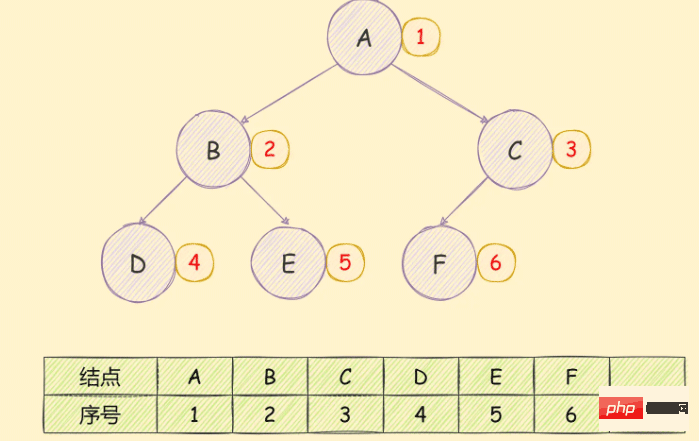
如果是一个非完全二叉树,如下图所示:
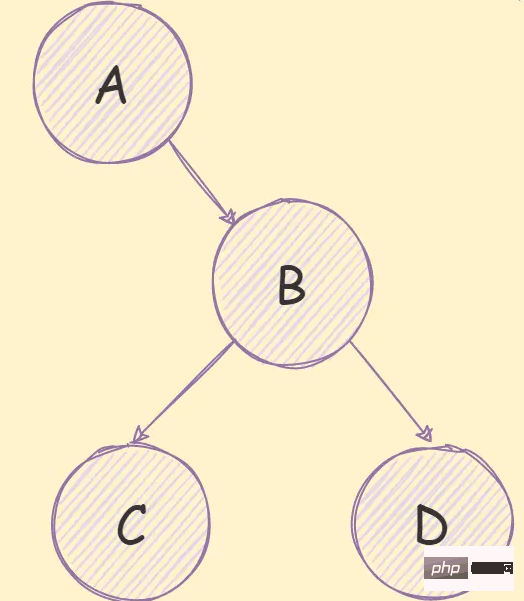
需要先将其转换为完全二叉树,然后在进行存储,如下图所示:
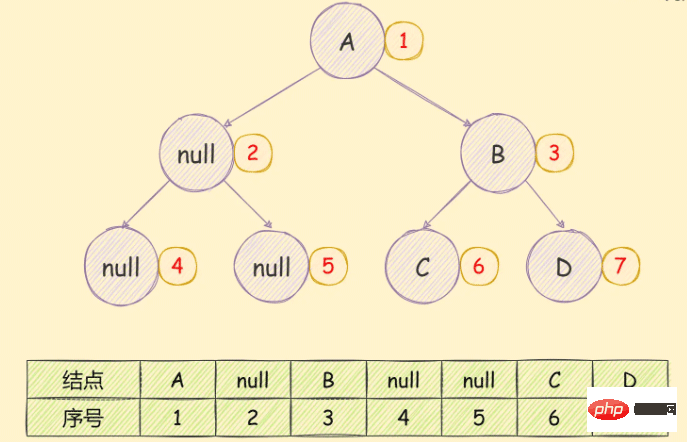
可以很明显的看到存储空间的浪费。
链表存储
使用链表存储通常将二叉树中的分为3个部分,如下图:

这三个部分依次是左子树的引用,该节点包含的数据,右子树的引用,存储方式如下图所示:
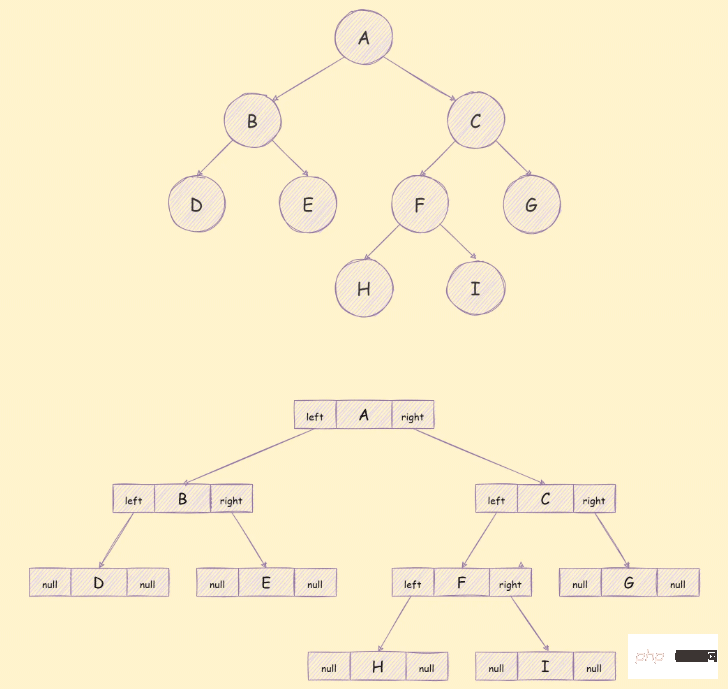
与二叉树相关的算法
以下算法中遍历用到的树如下:
// tree.js
const bt = {
val: 'A',
left: {
val: 'B',
left: { val: 'D', left: null, right: null },
right: { val: 'E', left: null, right: null },
},
right: {
val: 'C',
left: {
val: 'F',
left: { val: 'H', left: null, right: null },
right: { val: 'I', left: null, right: null },
},
right: { val: 'G', left: null, right: null },
},
}
module.exports = bt深度优先遍历
二叉树的深度优先遍历与树的深度优先遍历思路一致,思路如下:
- 访问根节点;
- 访问根节点的
left - 访问根节点的
right - 重复执行第二三步
实现代码如下:
const bt = {
val: 'A',
left: {
val: 'B',
left: { val: 'D', left: null, right: null },
right: { val: 'E', left: null, right: null },
},
right: {
val: 'C',
left: {
val: 'F',
left: { val: 'H', left: null, right: null },
right: { val: 'I', left: null, right: null },
},
right: { val: 'G', left: null, right: null },
},
}
function dfs(root) {
if (!root) return
console.log(root.val)
root.left && dfs(root.left)
root.right && dfs(root.right)
}
dfs(bt)
/** 结果
A B D E C F H I G
*/广度优先遍历
实现思路如下:
- 创建队列,把根节点入队
- 把对头出队并访问
- 把队头的
left和right Wenn die Tiefe dieses Binärbaums - Wenn in einem nicht leeren Binärbaum
n0die Anzahl der Blattknoten darstellt undn2die Anzahl der Nicht-Blattknoten mit Grad 2 ist, erfüllen die beiden die Anforderungen die Beziehungn0 = n2 + 1.
k beträgt, dann hat der Binärbaum höchstens 2^k-1 Knoten Vollständiger Binärbaum
Wenn in einem BinärbaumMit Ausnahme der Blattknoten der Grad jedes Knotens 2 beträgt, bedeutet dies, dass der Binärbaum ein vollständiger Binärbaum ist
,Wie in der Abbildung gezeigt Abbildung unten:
🎜🎜 🎜🎜🎜Zusätzlich zu befriedigend Vollständige Binärbäume haben neben den Eigenschaften gewöhnlicher Binärbäume auch die folgenden Eigenschaften: 🎜🎜🎜🎜Die
🎜🎜🎜Zusätzlich zu befriedigend Vollständige Binärbäume haben neben den Eigenschaften gewöhnlicher Binärbäume auch die folgenden Eigenschaften: 🎜🎜🎜🎜Die nte Ebene eines vollständigen Binärbaums hat 2^(n-1) Knoten; 🎜🎜Die Tiefe beträgt k<. der vollst bin von> muss <code>2^k-1 Knoten haben und die Anzahl der Blattknoten beträgt 2^( k-1); 🎜🎜hat Die Tiefe eines vollständigen Binärbaums mit n Knoten beträgt log_2^(n+1). 🎜🎜🎜Vollständiger Binärbaum🎜🎜🎜Wenn ein Binärbaum nach dem Entfernen der letzten Ebene ein vollständiger Binärbaum ist und der letzte Knoten 🎜von links nach rechts verteilt ist, dann ist der Binärbaum ein vollständiger Binärbaum, 🎜🎜🎜wie Wie in der folgenden Abbildung gezeigt: 🎜🎜🎜 🎜🎜Speicherung von Binärbäume🎜🎜Speicherung von Binärbäumen Es gibt zwei gängige Methoden: Die eine ist die Verwendung von 🎜Array-Speicher🎜 und die andere die Verwendung von verknüpften Listenspeichern. 🎜🎜Array-Speicher🎜🎜🎜Verwenden Sie Arrays zum Speichern von Binärbäumen. Wenn Sie auf einen vollständigen Binärbaum stoßen, erfolgt die Speicherreihenfolge von oben nach unten und von links nach rechts, wie in der folgenden Abbildung dargestellt: 🎜🎜🎜
🎜🎜Speicherung von Binärbäume🎜🎜Speicherung von Binärbäumen Es gibt zwei gängige Methoden: Die eine ist die Verwendung von 🎜Array-Speicher🎜 und die andere die Verwendung von verknüpften Listenspeichern. 🎜🎜Array-Speicher🎜🎜🎜Verwenden Sie Arrays zum Speichern von Binärbäumen. Wenn Sie auf einen vollständigen Binärbaum stoßen, erfolgt die Speicherreihenfolge von oben nach unten und von links nach rechts, wie in der folgenden Abbildung dargestellt: 🎜🎜🎜 🎜🎜🎜Wenn es sich um einen unvollständigen Binärbaum handelt, wie unten gezeigt: 🎜🎜🎜
🎜🎜🎜Wenn es sich um einen unvollständigen Binärbaum handelt, wie unten gezeigt: 🎜🎜🎜 🎜🎜🎜Sie müssen es in a konvertieren Vervollständigen Sie zuerst den Binärbaum und speichern Sie ihn dann, wie in der folgenden Abbildung gezeigt. Anzeige: 🎜🎜🎜
🎜🎜🎜Sie müssen es in a konvertieren Vervollständigen Sie zuerst den Binärbaum und speichern Sie ihn dann, wie in der folgenden Abbildung gezeigt. Anzeige: 🎜🎜🎜 🎜🎜Es ist deutlich zu erkennen, dass Speicherplatz verschwendet wird. 🎜🎜Verknüpfte Listenspeicherung🎜🎜🎜Bei Verwendung der verknüpften Listenspeicherung wird der Binärbaum normalerweise in drei Teile unterteilt, wie unten gezeigt: 🎜🎜🎜
🎜🎜Es ist deutlich zu erkennen, dass Speicherplatz verschwendet wird. 🎜🎜Verknüpfte Listenspeicherung🎜🎜🎜Bei Verwendung der verknüpften Listenspeicherung wird der Binärbaum normalerweise in drei Teile unterteilt, wie unten gezeigt: 🎜🎜🎜 🎜🎜🎜Diese drei Teile sind wiederum der Verweis auf den linken Teilbaum, die im Knoten enthaltenen Daten und der Verweis auf den rechten Teilbaum. Der Speicher Die Methode ist in der folgenden Abbildung dargestellt: 🎜🎜 🎜
🎜🎜🎜Diese drei Teile sind wiederum der Verweis auf den linken Teilbaum, die im Knoten enthaltenen Daten und der Verweis auf den rechten Teilbaum. Der Speicher Die Methode ist in der folgenden Abbildung dargestellt: 🎜🎜 🎜 🎜 🎜Algorithmen im Zusammenhang mit Binärbäumen🎜🎜🎜Die folgenden Algorithmen Der bei der Durchquerung verwendete Baum ist wie folgt🎜:🎜
🎜 🎜Algorithmen im Zusammenhang mit Binärbäumen🎜🎜🎜Die folgenden Algorithmen Der bei der Durchquerung verwendete Baum ist wie folgt🎜:🎜function bfs(root) {
if (!root) return
const queue = [root]
while (queue.length) {
const node = queue.shift()
console.log(node.val)
node.left && queue.push(node.left)
node.right && queue.push(node.right)
}
}
bfs(bt)
/** 结果
A B C D E F G H I
*/🎜Tiefendurchquerung🎜🎜🎜Die Tiefendurchquerung eines Binärbaums stimmt mit der Tiefendurchquerung überein Die Idee ist wie folgt: 🎜🎜🎜🎜Besuchen Sie den des Wurzelknotens🎜🎜Zugreifen Sie auf den Rechts der Wurzel Knoten🎜🎜 Wiederholen Sie den zweiten und dritten Schritt zur Warteschlange🎜🎜Entfernen Sie den Gegner aus der Warteschlange und greifen Sie darauf zu🎜🎜Geben Sie nacheinander links und rechts an der Spitze der Warteschlange ein🎜🎜Wiederholen Sie die Schritte 2 und 3, bis die Warteschlange ist leer🎜🎜🎜🎜Der Implementierungscode lautet wie folgt:🎜🎜const bt = require('./tree')
function preorder(root) {
if (!root) return
console.log(root.val)
preorder(root.left)
preorder(root.right)
}
preorder(bt)
/** 结果
A B D E C F H I G
*/🎜Vorbestellungsdurchquerung🎜🎜🎜Die Implementierungsidee der Vorbestellungsdurchquerung eines Binärbaums lautet wie folgt:🎜🎜- 访问根节点;
- 对当前节点的左子树进行先序遍历;
- 对当前节点的右子树进行先序遍历;
如下图所示:
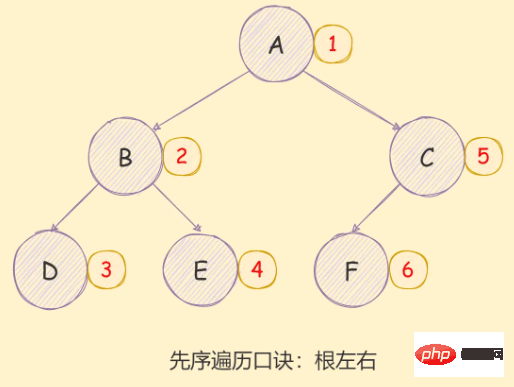
递归方式实现如下:
const bt = require('./tree')
function preorder(root) {
if (!root) return
console.log(root.val)
preorder(root.left)
preorder(root.right)
}
preorder(bt)
/** 结果
A B D E C F H I G
*/迭代方式实现如下:
// 非递归版
function preorder(root) {
if (!root) return
// 定义一个栈,用于存储数据
const stack = [root]
while (stack.length) {
const node = stack.pop()
console.log(node.val)
/* 由于栈存在先入后出的特性,所以需要先入右子树才能保证先出左子树 */
node.right && stack.push(node.right)
node.left && stack.push(node.left)
}
}
preorder(bt)
/** 结果
A B D E C F H I G
*/中序遍历
二叉树的中序遍历实现思想如下:
- 对当前节点的左子树进行中序遍历;
- 访问根节点;
- 对当前节点的右子树进行中序遍历;
如下图所示:
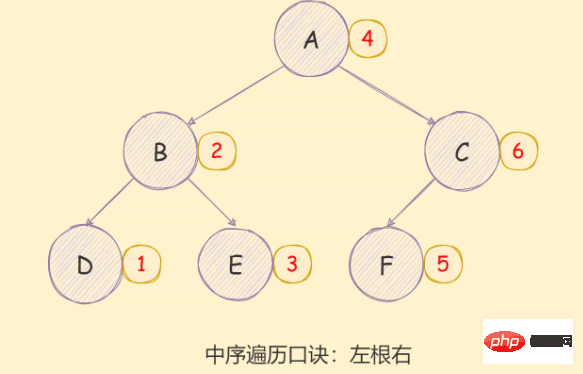
递归方式实现如下:
const bt = require('./tree')
// 递归版
function inorder(root) {
if (!root) return
inorder(root.left)
console.log(root.val)
inorder(root.right)
}
inorder(bt)
/** 结果
D B E A H F I C G
*/迭代方式实现如下:
// 非递归版
function inorder(root) {
if (!root) return
const stack = []
// 定义一个指针
let p = root
// 如果栈中有数据或者p不是null,则继续遍历
while (stack.length || p) {
// 如果p存在则一致将p入栈并移动指针
while (p) {
// 将 p 入栈,并以移动指针
stack.push(p)
p = p.left
}
const node = stack.pop()
console.log(node.val)
p = node.right
}
}
inorder(bt)
/** 结果
D B E A H F I C G
*/后序遍历
二叉树的后序遍历实现思想如下:
- 对当前节点的左子树进行后序遍历;
- 对当前节点的右子树进行后序遍历;
- 访问根节点;
如下图所示:
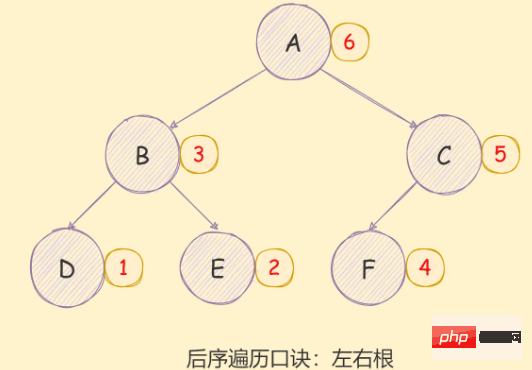
递归方式实现如下:
const bt = require('./tree')
// 递归版
function postorder(root) {
if (!root) return
postorder(root.left)
postorder(root.right)
console.log(root.val)
}
postorder(bt)
/** 结果
D E B H I F G C A
*/迭代方式实现如下:
// 非递归版
function postorder(root) {
if (!root) return
const outputStack = []
const stack = [root]
while (stack.length) {
const node = stack.pop()
outputStack.push(node)
// 这里先入left需要保证left后出,在stack中后出,就是在outputStack栈中先出
node.left && stack.push(node.left)
node.right && stack.push(node.right)
}
while (outputStack.length) {
const node = outputStack.pop()
console.log(node.val)
}
}
postorder(bt)
/** 结果
D E B H I F G C A
*/【相关推荐:javascript视频教程、web前端】
Das obige ist der detaillierte Inhalt vonDetaillierte Einführung in JavaScript-Binärbäume und verschiedene Traversalalgorithmen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Detaillierte Einführung in die Grundkonzepte und Verwendung von Promise in JavaScript
- Leicht verständliche JavaScript-Einführung
- Erfahren Sie mehr über die Prinzipien der JavaScript-Kompilierung
- Eine kurze Einführung in den JavaScript-„Prototyp' und die „Prototypkette'
- Zusammenfassung der grafischen JavaScript-Notizen mit 10.000 Wörtern

