Detaillierte Python-Analyse des binären Suchalgorithmus

Dieser Artikel vermittelt Ihnen relevantes Wissen über Python. Er organisiert hauptsächlich Probleme im Zusammenhang mit dem binären Suchalgorithmus, einschließlich Algorithmusbeschreibung, Algorithmusanalyse, Algorithmusideen usw. Ich hoffe, dass er Ihnen hilfreich sein wird Sie. Jeder ist hilfreich.

Empfohlenes Lernen: Python-Video-Tutorial

1. Algorithmusbeschreibung

Die Dichotomiemethode ist eine relativ effiziente Suchmethode

Erinnern Sie sich an das Zahlenschätzspiel, das Sie zuvor gespielt haben, und geben Sie einem vorgegebenen Ergebnis ein positives Ergebnis Ganzzahl x kleiner als 100 ermöglicht es Ihnen, die Größe zu erraten und Ihnen Tipps zu geben, wie Sie sie schnell erraten können.

Das Spiel, das wir zuvor erstellt haben, gibt 10 Chancen Um herauszufinden, wie hoch die Zahl ist, dauert es nur bis zu sieben Mal, die Zahl zu erraten.

2. Algorithmusanalyse

1 Es muss eine geordnete Reihenfolge sein.

2. Es gibt Anforderungen an die Datenmenge.

Die Datenmenge ist zu gering und für die binäre Suche nicht geeignet. Im Vergleich zur direkten Durchquerung ist die Effizienzverbesserung nicht offensichtlich.

Es ist nicht geeignet, die binäre Suche zu verwenden, wenn die Datenmenge zu groß ist, da das Array kontinuierlichen Speicherplatz benötigt. Wenn die Datenmenge zu groß ist, wird häufig kein kontinuierlicher Speicherplatz zum Speichern solch großer Datenmengen gefunden . .

3. Algorithmusidee

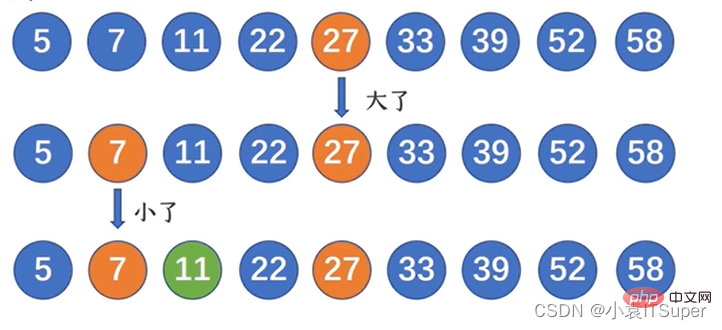
Angenommen, es gibt eine geordnete Liste wie folgt:



Ist die Nummer 11 in dieser Liste?

4 Implementierung

Reine Algorithmusimplementierung

Implementierungscode:

arr_list = [5, 7, 11, 22, 27, 33, 39, 52, 58]# 需要查找的数字seek_number = 11# 保存一共查找了几次count = 0# 列表左侧索引left = 0# 列表右侧索引right = len(arr_list) - 1# 当左侧索引小于等于右侧索引时while left  arr_list[middle]:
        # 左侧索引为中间位置索引+1
        left = middle + 1
    # 如果查找的数字小于中间位置的数字时
    elif seek_number <p>Laufendes Ergebnis:</p><p><img src="https://img.php.cn/upload/article/000/000/067/ab7ca007166584d2196443b3030f239a-4.png" alt="Detaillierte Python-Analyse des binären Suchalgorithmus"></p><h2>Rekursive Methodenimplementierung</h2><blockquote>
<p>Eine Variablenanzahl wird in der Schleife definiert. Wenn sich die Anzahl nach der ersten Schleife nicht ändert, bedeutet dies dass die Eingabe eine geordnete Sequenz ist. Zu diesem Zeitpunkt kehren wir direkt zurück, um die Schleife zu verlassen. Die Zeitkomplexität beträgt zu diesem Zeitpunkt O(n). : </p>Python-Video-Tutorial</blockquote> <p></p>

Das obige ist der detaillierte Inhalt vonDetaillierte Python-Analyse des binären Suchalgorithmus. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!