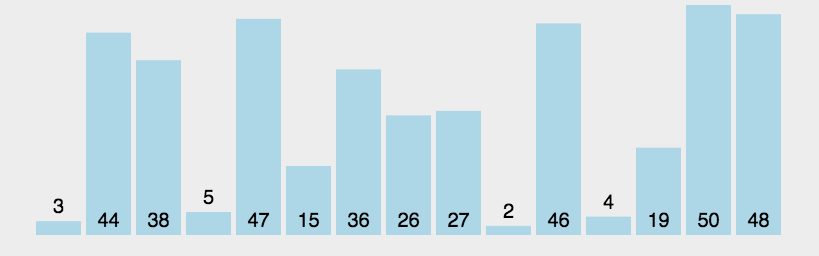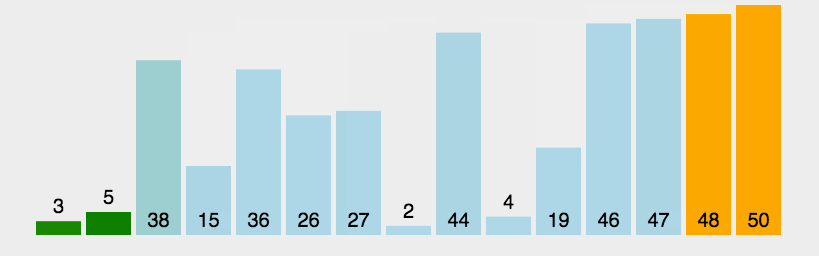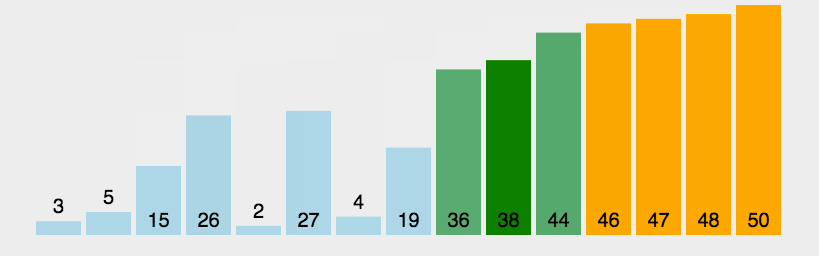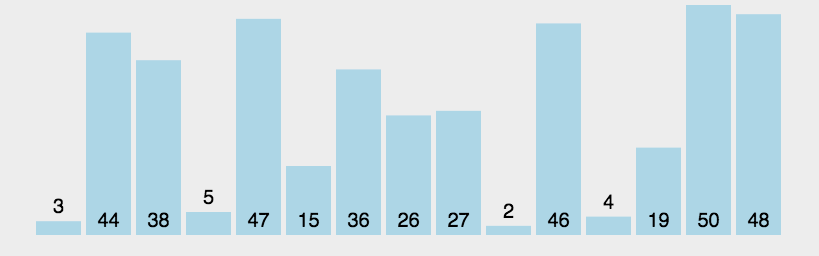Heim >Backend-Entwicklung >Python-Tutorial >Detaillierte grafische Erklärung des Python-Blasensortierungsalgorithmus
Detaillierte grafische Erklärung des Python-Blasensortierungsalgorithmus
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2022-06-06 19:21:083631Durchsuche
Dieser Artikel vermittelt Ihnen relevantes Wissen über Python. Er stellt hauptsächlich verwandte Themen zur Blasensortierung vor, einschließlich Algorithmusbeschreibung, Analyse, Codeimplementierung usw. Ich hoffe, dass er für Sie hilfreich ist ist hilfreich.

Empfohlenes Lernen: Python-Video-Tutorial
1. Algorithmusbeschreibung
Bubble Sort (Bubble Sort) ist ein einfacher Sortieralgorithmus. Es durchläuft wiederholt das zu sortierende Array, vergleicht jeweils zwei Elemente und vertauscht sie, wenn sie in der falschen Reihenfolge sind. Die Arbeit des Durchlaufens des Arrays wird wiederholt, bis kein Austausch mehr erforderlich ist, was bedeutet, dass das Array sortiert wurde. Der Name dieses Algorithmus rührt von der Tatsache her, dass kleinere Elemente durch den Austausch langsam an die Spitze des Arrays „schweben“.
2. Algorithmusanalyse
1. Wenn der erste größer als der zweite ist (in aufsteigender Reihenfolge), tauschen Sie beide aus.
2. Machen Sie dasselbe für jedes Paar benachbarter Elemente, vom ersten Paar am Anfang bis zum letzten Paar am Ende. Nachdem dieser Schritt abgeschlossen ist, ist das letzte Element die größte Zahl.
3. Wiederholen Sie die obigen Schritte für alle Elemente außer dem letzten.
4. Wiederholen Sie die obigen Schritte jedes Mal für immer weniger Elemente, bis keine Zahlenpaare mehr zum Vergleichen vorhanden sind.
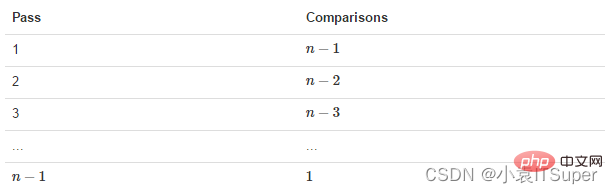
Dann müssen wir n-1 Bubbling-Prozesse durchführen, und die entsprechende Anzahl von Vergleichen ist in der folgenden Abbildung dargestellt:
3. Animationsanzeige
4. Code-Implementierungzum Verständnis Werfen wir einen Blick auf die Animationsimplementierung
Wir sortieren die folgende ungeordnete Liste:5 . Algorithmus-Upgradeimport timepop_list = [19, 14, 10, 4, 15, 26, 20, 96]print("没排序前的列表为:", pop_list)# 记录开始时间start = time.time()# 外层循环控制轮数for i in range(len(pop_list) - 1): # 内层循环控制比较次数 for j in range(len(pop_list) - i - 1): # 如果前一个数字比后一个数字大,就交换位置 if pop_list[j] > pop_list[j + 1]: # python特有交换位置方式 pop_list[j], pop_list[j + 1] = pop_list[j + 1], pop_list[j]print("排序好的列表为:", pop_list)# 记录结束时间end = time.time()print("算法总耗时:", end - start)
Laufende Ergebnisse:
Wenn sich die Anzahl nach der ersten Schleife nicht ändert, bedeutet dies, dass es sich bei der Eingabe um eine geordnete Sequenz handelt Die zeitliche Komplexität beträgt derzeit 
import timedef bubble_sort(pop_list): for j in range(len(pop_list) - 1, 0, -1): count = 0 for i in range(0, j): if pop_list[i] > pop_list[i + 1]: pop_list[i], pop_list[i + 1] = pop_list[i + 1], pop_list[i] count += 1 if count == 0: returnpop_list = [19, 14, 10, 4, 15, 26, 20, 96]print("没排序前的列表为:", pop_list)# 记录开始时间start = time.time()bubble_sort(pop_list)print("排序好的列表为:", pop_list)# 记录结束时间end = time.time()print("算法总耗时:", end - start)Laufendes Ergebnis:
O(n)
6. Zeitkomplexitätsanalyse
🎜🎜🎜Sortierungsanalyse: Es gibt eine Insgesamt 8 Zahlen im zu sortierenden Array wurden 7 Vergleiche in der ersten Sortierrunde durchgeführt, 6 Vergleiche wurden in der zweiten Sortierrunde durchgeführt usw. und 1 Vergleich wurde in der letzten Runde durchgeführt.Die schlechteste Zeitkomplexität:
- Optimale Zeitkomplexität:
O(n)(Zeigt an, dass nach einmaligem Durchlaufen festgestellt wird, dass keine Elemente ausgetauscht werden können, und die Sortierung endet .)O(n)(表示遍历一次发现没有任何可以交换的元素,排序结束。)- 最坏时间复杂度:
O(n^2)- 稳定性:稳定
- 排序分析:待排数组中一共有8个数,第一轮排序时进行了7次比较,第二轮排序时进行了6比较,依次类推,最后一轮进行了1次比较。
- 数组元素总数为N时,则一共需要的比较次数为:
(N-1)+ (N-2)+ (N-3)+ ...1=N*(N-1)/2- 算法约做了
N^2/2次比较。因为只有在前面的元素比后面的元素大时才交换数据,所以交换的次数少于比较的次数。如果数据是随机的,大概有一半数据需要交换,则交换的次数为N^2/4(不过在最坏情况下,即初始数据逆序时,每次比较都需要交换)。- 交换和比较的操作次数都与 N^2 成正比,由于在大O表示法中,常数忽略不计,冒泡排序的时间复杂度为
O(N^2)O(n^2)
🎜🎜🎜🎜Wenn die Gesamtzahl der Array-Elemente N beträgt, ist die Gesamtzahl der erforderlichen Vergleiche:
(N-1)+ (N-2)+ (N-3) + .. .1=N*(N-1)/2Der 🎜🎜🎜🎜-Algorithmus führt ungefähr
N^2/2 Vergleiche durch. Da Daten nur dann ausgetauscht werden, wenn das vorhergehende Element größer als das folgende Element ist, ist die Anzahl der Austauschvorgänge geringer als die Anzahl der Vergleiche. Wenn die Daten zufällig sind und etwa die Hälfte der Daten ausgetauscht werden muss, beträgt die Anzahl der Austausche N^2/4 (aber im schlimmsten Fall, wenn die Anfangsdaten in umgekehrter Reihenfolge vorliegen, alle Vergleich muss ausgetauscht werden). 🎜🎜🎜🎜Die Anzahl der Austausch- und Vergleichsoperationen ist proportional zu N^2. Da in der großen O-Notation Konstanten ignoriert werden, beträgt die Zeitkomplexität der Blasensortierung
O (N ^2). 🎜🎜🎜🎜🎜Empfohlenes Lernen: 🎜Python-Video-Tutorial🎜🎜Das obige ist der detaillierte Inhalt vonDetaillierte grafische Erklärung des Python-Blasensortierungsalgorithmus. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Zusammenfassung der Wissenspunkte zu Python-Multiprozessen
- Detaillierte Einführung in das Numpy-Modul von Python
- Detaillierte grafische Erklärung, wie man Python zum Zeichnen dynamischer Visualisierungsdiagramme verwendet
- Detaillierte Beispiele der vier objektorientierten Funktionen von Python
- Python-Datenanalyse-Concat- und Merge-Funktionen (detaillierte Beispiele)