Heim >Backend-Entwicklung >Python-Tutorial >Erkennung und Verarbeitung von Python-Datenausreißern (detaillierte Beispiele)
Erkennung und Verarbeitung von Python-Datenausreißern (detaillierte Beispiele)
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2022-03-04 17:58:2820954Durchsuche
Dieser Artikel vermittelt Ihnen relevantes Wissen über Python, das hauptsächlich Probleme im Zusammenhang mit Ausreißern bei der Datenanalyse vorstellt. Im Allgemeinen umfassen die Erkennungsmethoden für Ausreißer statistische Methoden, Clustering-basierte Methoden und einige spezielle Methoden zur Erkennung von Ausreißern usw. Diese Im Folgenden werden die Methoden vorgestellt. Ich hoffe, dass sie für alle hilfreich sind.

Empfohlenes Lernen: Python-Lern-Tutorial
1 Was ist ein Ausreißer?
Beim maschinellen Lernen ist die Anomalieerkennung und -verarbeitung ein relativ kleiner Zweig oder mit anderen Worten ein Nebenprodukt des maschinellen Lernens, da das Modell bei allgemeinen Vorhersageproblemen normalerweise eine Analyse der gesamten Stichprobendatenstruktur ist Dieser Ausdruck erfasst normalerweise die allgemeinen Eigenschaften der Gesamtstichprobe, und die Punkte, die hinsichtlich dieser Eigenschaften völlig unvereinbar sind, werden bei Vorhersageproblemen normalerweise nicht verwendet, da Vorhersagen nicht beliebt sind Probleme konzentrieren sich im Allgemeinen auf die Eigenschaften der Gesamtstichprobe, und der Generierungsmechanismus von Ausreißern stimmt nicht mit der Gesamtstichprobe überein. Wenn der Algorithmus empfindlich auf Ausreißer reagiert, kann das generierte Modell die Gesamtstichprobe nicht vorhersagen Die Vorhersage wird ungenau sein. Andererseits sind abnormale Punkte für Analysten in bestimmten Szenarien von großem Interesse. Normalerweise sind die physischen Indikatoren gesunder Menschen in einigen Dimensionen ähnlich. Wenn eine Anomalie vorliegt Sein körperlicher Zustand muss sich in einigen Aspekten verändert haben. Natürlich ist diese Veränderung nicht unbedingt auf die Krankheit zurückzuführen (oft als Rauschpunkt bezeichnet), aber das Auftreten und die Erkennung von Anomalien sind ein wichtiger Ausgangspunkt für die Krankheitsvorhersage. Ähnliche Szenarien lassen sich auch bei Kreditbetrug, Cyberangriffen etc. anwenden.
2 Erkennungsmethoden für Ausreißer Zu den allgemeinen Erkennungsmethoden für Ausreißer gehören statistische Methoden, Clustering-basierte Methoden und einige Methoden, die auf die Erkennung von Ausreißern spezialisiert sind. Diese Methoden werden im Folgenden vorgestellt. 1. Einfache StatistikenWenn Siepandas verwenden, können wir describe() direkt verwenden, um die statistische Beschreibung der Daten zu beobachten (einige Statistiken nur grob beobachten), Die Statistiken sind jedoch kontinuierlich und wie folgt:
df.describe()
pandas,我们可以直接使用describe()来观察数据的统计性描述(只是粗略的观察一些统计量),不过统计数据为连续型的,如下:Percentile = np.percentile(df['length'],[0,25,50,75,100]) IQR = Percentile[3] - Percentile[1] UpLimit = Percentile[3]+ageIQR*1.5 DownLimit = Percentile[1]-ageIQR*1.5

或者简单使用散点图也能很清晰的观察到异常值的存在。如下所示:

2. 3∂原则
这个原则有个条件:数据需要服从正态分布。在3∂原则下,异常值如超过3倍标准差,那么可以将其视为异常值。正负3∂的概率是99.7%,那么距离平均值3∂之外的值出现的概率为P(|x-u| > 3∂) <= 0.003,属于极个别的小概率事件。如果数据不服从正态分布,也可以用远离平均值的多少倍标准差来描述。

红色箭头所指就是异常值。
3. 箱型图
这种方法是利用箱型图的四分位距(IQR)对异常值进行检测,也叫Tukey‘s test。箱型图的定义如下:

四分位距(IQR)就是上四分位与下四分位的差值。而我们通过IQR的1.5倍为标准,规定:超过上四分位+1.5倍IQR距离,或者下四分位-1.5倍IQR距离的点为异常值。下面是Python中的代码实现,主要使用了numpy的percentile方法。
f,ax=plt.subplots(figsize=(10,8)) sns.boxplot(y='length',data=df,ax=ax) plt.show()
也可以使用seaborn的可视化方法boxplot
Oder verwenden Sie einfach ein Streudiagramm, um die Existenz von Ausreißern klar zu erkennen. Wie unten gezeigt: 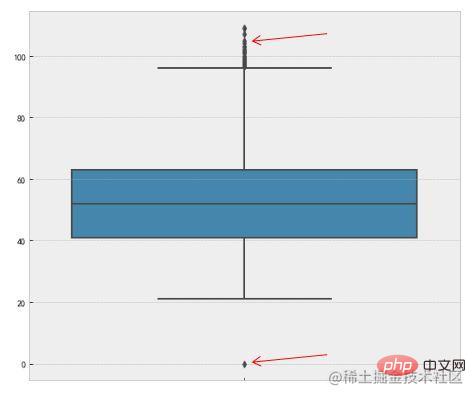
 2 Für dieses Prinzip gilt eine Bedingung:
2 Für dieses Prinzip gilt eine Bedingung: Die Daten müssen der Normalverteilung entsprechen
. Wenn ein Ausreißer nach dem 3∂-Prinzip das Dreifache der Standardabweichung überschreitet, kann er als Ausreißer betrachtet werden. Die Wahrscheinlichkeit, dass 3∂ positiv oder negativ ist, beträgt 99,7 %, sodass die Wahrscheinlichkeit, dass ein anderer Wert als 3∂ vom Durchschnittswert auftritt, P(|x-u| > 3∂) <= 0,003 ist, was sehr selten und gering ist Wahrscheinlichkeitsereignis. Wenn die Daten keiner Normalverteilung folgen, kann sie auch dadurch beschrieben werden, wie oft die Standardabweichung vom Mittelwert abweicht.
3. Boxplot
Diese Methode nutzt den 🎜Interquartilbereich (IQR)🎜 des Boxplots, um Ausreißer zu erkennen, auch 🎜Tukey-Test🎜 genannt. Die Definition des Boxplots lautet wie folgt: 🎜🎜 🎜🎜 vier Punkte Der IQR ist die Differenz zwischen dem oberen Quartil und dem unteren Quartil. Wir verwenden das 1,5-fache des IQR als Standard und legen fest, dass Punkte, die das obere Quartil + 1,5-fache IQR-Distanz oder das untere Quartil – 1,5-fache IQR-Distanz 🎜 überschreiten, Ausreißer sind. Das Folgende ist die Code-Implementierung in Python, die hauptsächlich die
🎜🎜 vier Punkte Der IQR ist die Differenz zwischen dem oberen Quartil und dem unteren Quartil. Wir verwenden das 1,5-fache des IQR als Standard und legen fest, dass Punkte, die das obere Quartil + 1,5-fache IQR-Distanz oder das untere Quartil – 1,5-fache IQR-Distanz 🎜 überschreiten, Ausreißer sind. Das Folgende ist die Code-Implementierung in Python, die hauptsächlich die percentile-Methode von numpy verwendet. 🎜rrreee🎜Sie können auch die Visualisierungsmethode boxplot von seaborn verwenden, um dies zu erreichen: 🎜rrreee🎜🎜🎜🎜Der rote Pfeil zeigt auf den Ausreißer. 🎜🎜Das Obige ist eine einfache Methode, die häufig zur Bestimmung von Ausreißern verwendet wird. Lassen Sie uns einige komplexere Ausreißererkennungsalgorithmen vorstellen. Da es sich um viele Inhalte handelt, werden nur die Kernideen vorgestellt. Interessierte Freunde können sich eingehend damit befassen. 🎜🎜4. Basierend auf der Modellerkennung🎜🎜Diese Methode erstellt im Allgemeinen ein 🎜Wahrscheinlichkeitsverteilungsmodell🎜 und berechnet die Wahrscheinlichkeit, dass das Objekt dem Modell entspricht, und behandelt Objekte mit geringer Wahrscheinlichkeit als Ausreißer. Wenn es sich bei dem Modell um eine Sammlung von Clustern handelt, handelt es sich bei Anomalien um Objekte, die nicht wesentlich zu einem Cluster gehören. Bei einem Regressionsmodell handelt es sich um Objekte, die relativ weit vom vorhergesagten Wert entfernt sind. 🎜🎜Wahrscheinlichkeitsdefinition von Ausreißern: 🎜Ein Ausreißer ist ein Objekt, das eine geringe Wahrscheinlichkeit 🎜 in Bezug auf das Wahrscheinlichkeitsverteilungsmodell der Daten aufweist. Die Voraussetzung für diese Situation besteht darin, zu wissen, welcher Verteilung der Datensatz folgt. Wenn die Schätzung falsch ist, entsteht eine stark ausgeprägte Verteilung. 🎜Zum Beispiel verwendet die RobustScaler-Methode im Feature-Engineering beim Skalieren von Daten-Feature-Werten die Quantilverteilung von Daten-Features, um die Daten entsprechend dem Quantil in mehrere Segmente zu unterteilen und nur das mittlere Segment zu verwenden Um beispielsweise eine Skalierung durchzuführen, nehmen Sie für die Skalierung nur die Daten vom 25 %-Quantil bis zum 75 %-Quantil. Dadurch werden die Auswirkungen abnormaler Daten verringert. RobustScaler方法,在做数据特征值缩放的时候,它会利用数据特征的分位数分布,将数据根据分位数划分为多段,只取中间段来做缩放,比如只取25%分位数到75%分位数的数据做缩放。这样减小了异常数据的影响。
优缺点:(1)有坚实的统计学理论基础,当存在充分的数据和所用的检验类型的知识时,这些检验可能非常有效;(2)对于多元数据,可用的选择少一些,并且对于高维数据,这些检测可能性很差。
5. 基于近邻度的离群点检测
统计方法是利用数据的分布来观察异常值,一些方法甚至需要一些分布条件,而在实际中数据的分布很难达到一些假设条件,在使用上有一定的局限性。
确定数据集的有意义的邻近性度量比确定它的统计分布更容易。这种方法比统计学方法更一般、更容易使用,因为一个对象的离群点得分由到它的k-最近邻(KNN)的距离给定。
需要注意的是:离群点得分对k的取值高度敏感。如果k太小,则少量的邻近离群点可能导致较低的离群点得分;如果K太大,则点数少于k的簇中所有的对象可能都成了离群点。为了使该方案对于k的选取更具有鲁棒性,可以使用k个最近邻的平均距离。
优缺点:(1)简单;(2)缺点:基于邻近度的方法需要O(m2)时间,大数据集不适用;(3)该方法对参数的选择也是敏感的;(4)不能处理具有不同密度区域的数据集,因为它使用全局阈值,不能考虑这种密度的变化。
5. 基于密度的离群点检测
从基于密度的观点来说,离群点是在低密度区域中的对象。基于密度的离群点检测与基于邻近度的离群点检测密切相关,因为密度通常用邻近度定义。一种常用的定义密度的方法是,定义密度为到k个最近邻的平均距离的倒数。如果该距离小,则密度高,反之亦然。另一种密度定义是使用DBSCAN聚类算法使用的密度定义,即一个对象周围的密度等于该对象指定距离d内对象的个数。
优缺点:(1)给出了对象是离群点的定量度量,并且即使数据具有不同的区域也能够很好的处理;(2)与基于距离的方法一样,这些方法必然具有O(m2)的时间复杂度。对于低维数据使用特定的数据结构可以达到O(mlogm);(3)参数选择是困难的。虽然LOF算法通过观察不同的k值,然后取得最大离群点得分来处理该问题,但是,仍然需要选择这些值的上下界。
6. 基于聚类的方法来做异常点检测
基于聚类的离群点:一个对象是基于聚类的离群点,如果该对象不强属于任何簇,那么该对象属于离群点。
离群点对初始聚类的影响:如果通过聚类检测离群点,则由于离群点影响聚类,存在一个问题:结构是否有效。这也是k-means算法的缺点,对离群点敏感。为了处理该问题,可以使用如下方法:对象聚类,删除离群点,对象再次聚类(这个不能保证产生最优结果)。
优缺点:(1)基于线性和接近线性复杂度(k均值)的聚类技术来发现离群点可能是高度有效的;(2)簇的定义通常是离群点的补,因此可能同时发现簇和离群点;(3)产生的离群点集和它们的得分可能非常依赖所用的簇的个数和数据中离群点的存在性;(4)聚类算法产生的簇的质量对该算法产生的离群点的质量影响非常大。
7. 专门的离群点检测
其实以上说到聚类方法的本意是是无监督分类,并不是为了寻找离群点的,只是恰好它的功能可以实现离群点的检测,算是一个衍生的功能。
除了以上提及的方法,还有两个专门用于检测异常点的方法比较常用:One Class SVM和Isolation Forest
5. Ausreißererkennung basierend auf der Nähe
Statistische Methoden nutzen die Verteilung von Daten, um Ausreißer zu beobachten. In der Praxis ist die Verteilung von Daten schwierig zu erreichen. Es gibt bestimmte Einschränkungen bei der Verwendung. Es ist einfacher, ein aussagekräftiges Maß für die Nähe eines Datensatzes zu bestimmen, als seine statistische Verteilung zu bestimmen. Diese Methode ist allgemeiner und einfacher zu verwenden als statistische Methoden, da die Ausreißerbewertung eines Objekts durch die Entfernung zu seinen k-nächsten Nachbarn (KNN) gegeben ist. 🎜🎜Es ist zu beachten, dass der Ausreißer-Score sehr empfindlich auf den Wert von k reagiert. Wenn k zu klein ist, kann eine kleine Anzahl von Ausreißern in der Nähe zu einem niedrigen Ausreißerwert führen. Wenn K zu groß ist, können alle Objekte in Clustern mit weniger als k Punkten zu Ausreißern werden. Um dieses Schema robuster gegenüber der Auswahl von k zu machen, kann der durchschnittliche Abstand der k nächsten Nachbarn verwendet werden. 🎜🎜Vorteile und Nachteile: (1) Einfach; (2) Nachteile: Die auf Nähe basierende Methode benötigt O(m2) Zeit und ist nicht für große Datensätze geeignet; Diese Methode ist geeignet für: Die Wahl der Parameter ist ebenfalls empfindlich. (4) Sie kann keine Datensätze mit Regionen unterschiedlicher Dichte verarbeiten, da sie einen globalen Schwellenwert verwendet und solche Dichteänderungen nicht berücksichtigen kann. 🎜
5. Dichtebasierte Ausreißererkennung
🎜Aus dichtebasierter Sicht sind Ausreißer Objekte in Bereichen mit geringer Dichte. Die dichtebasierte Ausreißererkennung ist eng mit der nähebasierten Ausreißererkennung verwandt, da die Dichte häufig anhand der Nähe definiert wird. Eine übliche Methode zur Definition der Dichte besteht darin, die Dichte als Kehrwert des durchschnittlichen Abstands zu den k nächsten Nachbarn zu definieren. Ist dieser Abstand klein, ist die Dichte hoch und umgekehrt. Eine weitere Definition der Dichte ist die vom DBSCAN-Clustering-Algorithmus verwendete Dichtedefinition, d. h. die Dichte um ein Objekt herum ist gleich der Anzahl der Objekte innerhalb einer bestimmten Entfernung d vom Objekt. 🎜🎜Vor- und Nachteile:(1) Es gibt ein quantitatives Maß dafür, dass das Objekt ein Ausreißer ist, und kann damit gut umgehen, selbst wenn die Daten unterschiedliche Bereiche haben; Die Distanzmethode ist dieselbe und diese Methoden müssen eine Zeitkomplexität von O (m2) haben. Bei niedrigdimensionalen Daten kann die Verwendung spezifischer DatenstrukturenO(mlogm) erreichen. (3) Die Parameterauswahl ist schwierig. Obwohl der LOF-Algorithmus dieses Problem löst, indem er verschiedene k-Werte beobachtet und dann den maximalen Ausreißerwert ermittelt, muss er dennoch Ober- und Untergrenzen für diese Werte auswählen. 🎜6. Clustering-basierte Methode zur Ausreißererkennung
🎜Clustering-basierte Ausreißer:Ein Objekt ist ein Clustering-basierter Ausreißer, wenn das Objekt keinem Cluster eindeutig angehört ein Ausreißer. 🎜🎜Der Einfluss von Ausreißern auf das anfängliche Clustering: Wenn Ausreißer durch Clustering erkannt werden, stellt sich die Frage, ob die Struktur gültig ist, da die Ausreißer das Clustering beeinflussen. Dies ist auch ein Manko desk-means-Algorithmus, der empfindlich auf Ausreißer reagiert. Um dieses Problem zu lösen, können die folgenden Methoden verwendet werden: Objekt-Clustering, Löschen von Ausreißern und erneutes Clustering von Objekten (dies garantiert keine optimalen Ergebnisse). 🎜🎜Vor- und Nachteile: (1) Clustering-Techniken, die auf linearer und nahezu linearer Komplexität (k-Mittelwerte) basieren, können bei der Erkennung von Ausreißern sehr effektiv sein. (2) Die Definition von Clustern erfolgt normalerweise anhand von Ausreißern. Komplementierung von Clusterpunkten, sodass Cluster und Ausreißer gleichzeitig entdeckt werden können. (3) Die resultierenden Ausreißermengen und ihre Bewertungen können stark von der Anzahl der verwendeten Cluster und dem Vorhandensein von Ausreißern in den Daten abhängen Die Anzahl der von einem Clustering-Algorithmus erzeugten Cluster hat einen großen Einfluss auf die Qualität der vom Algorithmus erzeugten Ausreißer. 🎜7. Spezialisierte Ausreißererkennung
🎜Tatsächlich besteht die ursprüngliche Absicht der oben erwähnten Clustering-Methode nicht darin, Ausreißer zu finden, sondern nur darin, dass ihre Funktion Ausreißer erkennen kann. Die Punkterkennung ist eine abgeleitete Funktion. 🎜🎜Zusätzlich zu den oben genannten Methoden gibt es zwei weitere häufig verwendete Methoden, die speziell zur Erkennung von Ausreißern verwendet werden:One Class SVM und Isolation Forest. Auf die Details wird nicht eingegangen Tiefe Forschung. 🎜🎜3 Wie man mit Ausreißern umgeht🎜🎜Ausreißer wurden erkannt und wir müssen bis zu einem gewissen Grad damit umgehen. Die allgemeinen Methoden zum Umgang mit Ausreißern lassen sich grob in die folgenden Kategorien einteilen: 🎜- Datensätze mit Ausreißern löschen: Datensätze mit Ausreißern direkt löschen;
- Als fehlende Werte behandeln: Ausreißer als fehlende Werte behandeln und Methoden zur Verarbeitung fehlender Werte verwenden Der Durchschnitt der beiden beobachteten Werte davor und danach kann verwendet werden, um den Ausreißer zu korrigieren Situation berücksichtigen. Da einige Modelle nicht sehr empfindlich auf Ausreißer reagieren, selbst wenn es Ausreißer gibt, wird der Modelleffekt nicht beeinträchtigt. Einige Modelle wie die logistische Regression LR reagieren jedoch sehr empfindlich auf Ausreißer, wenn sie nicht verarbeitet werden geschehen. 4 Zusammenfassung der Ausreißer
- Das Obige ist eine Zusammenfassung der Methoden zur Erkennung und Verarbeitung von Ausreißern. Mit einigen Erkennungsmethoden können wir Ausreißer finden, aber die erzielten Ergebnisse sind nicht absolut korrekt. Die spezifische Situation muss auf der Grundlage des Verständnisses des Unternehmens beurteilt werden. Ebenso muss der Umgang mit Ausreißern, ob sie gelöscht, korrigiert oder nicht verarbeitet werden sollen, auf der Grundlage der tatsächlichen Situation berücksichtigt werden und ist nicht festgelegt.
- Empfohlenes Lernen: Python-Tutorial
Das obige ist der detaillierte Inhalt vonErkennung und Verarbeitung von Python-Datenausreißern (detaillierte Beispiele). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Teilen Sie 10 interessante und praktische Python-Module und sehen Sie sich ihre Funktionen an!
- Python implementiert das Lesen von Höheninformationen in DEM mithilfe von Breiten- und Längengrad-Punktkoordinaten (detailliertes Beispiel).
- Eine kurze Analyse der Verwendung des Python-Formats
- Python lernt, das Funktionsprinzip von Flask zu analysieren (ausführliche Erklärung mit Bildern und Texten)
- Nehmen Sie an der Interpretation von Python-Multithreading teil

